An augmented Lagrangian optimization method for inflatable structures analysis problems

Abstract

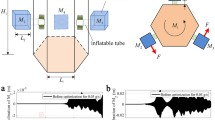
This paper describes the development of an augmented Lagrangian optimization method for the numerical simulation of the inflation process in the design of inflatable space structures. Although the Newton–Raphson scheme was proven to be efficient for solving many nonlinear problems, it can lead to lack of convergence when it is applied to the simulation of the inflation process. As a result, it is recommended to use an optimization algorithm to find the minimum energy configuration that satisfies the equilibrium equations characterizing the final shape of the inflated structure subject to an internal pressure. On top of that, given that some degrees of freedom may be linked, the optimum may be constrained, and specific optimization methods for constrained problems must be considered. The paper presents the formulation and the augmented Lagrangian method (ALM) developed in SAMCEF Mecano for inflatable structures analysis problems. The related quasi-unconstrained optimization problem is solved with a nonlinear conjugate gradient method. The Wolfe conditions are used in conjunction with a cubic interpolation for the line search. Equality constraints are considered and can be easily treated by the ALM formulation. Numerical applications present simulations of unconstrained and constrained inflation processes (i.e., where the motion of some nodes is ruled by a rigid body element restriction and/or problems including contact conditions).