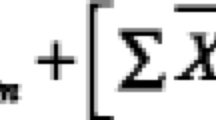Abstract
This study examines the gender wage gap in the USA using two separate cross-sections from the Current Population Survey (CPS). The extensive literature on this subject includes wage decompositions that divide the gender wage gap into “explained” and “unexplained” components. One of the problems with this approach is the heterogeneity of the sample data. In order to address the difficulties of comparing like with like, this study uses a number of different matching techniques to obtain estimates of the gap. By controlling for a wide range of other influences, in effect, we estimate the direct effect of simply being female on wages. However, a number of other factors, such as parenthood, gender segregation, part-time working, and unionization, contribute to the gender wage gap. This means that it is not just the core “like for like” comparison between male and female wages that matters but also how gender wage differences interact with other influences. The literature has noted the existence of these interactions, but precise or systematic estimates of such effects remain scarce. The most innovative contribution of this study is to do that. Our findings imply that the idea of a single uniform gender pay gap is perhaps less useful than an understanding of how gender wages are shaped by multiple different forces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This study estimates the gender pay gap in the USA using several different matching estimators. We first justify the use of matching estimators by using an Oaxaca recentered influence function (RIF) model to estimate the gender pay gap. Other authors using a similar approach have found the “unexplained” component of the gender pay gap to be high. Some of these, including Kassenboehmer and Sinning (2014) and Töpfer (2017), attribute this to heterogeneity within their sample. A similar analysis in this study also finds a high “unexplained” component, which implies a heterogeneity problem.
Where heterogeneity is an issue, a well-established approach is to use a matching estimator—see, for example, Ñopo (2008). This study therefore relies on several matching estimators for its core analysis. These are discussed from the methodological perspective later, but matching involves a number of conceptual issues which are central to the approach of this study. A matching approach creates a control group (of males) which, as far as possible, matches the treated group (female) in all relevant characteristics. For the estimator not to be biased, relevant characteristics such as part-time working and union membership must be included as covariates. The result is an estimate of the gap between male and female pay that controls for all relevant observable characteristics, including unionization and part-time work. Estimating a pure “gender” effect on wages is one of the advantages of using a matching estimator, but the process of creating a control group omits other more indirect ways by which women are paid less.
For example, working part-time typically involves a substantially lower hourly rate of pay than working full-time, as this study confirms. A much higher proportion of females work part-time than do males. Likewise, unionized workers exhibit significantly higher hourly pay than non-unionized workers, and females are much less likely to be unionized than males. A matching approach is intended to capture the effect on wages of being female and needs to control for overlapping effects like part-time work or union membership. Methodologically this is sound, but it must be properly understood that there is more to the matter. In terms of hourly pay, females are also disadvantaged by, say, working part-time and being less likely to be unionized. It is proper to ignore such effects in a matching estimate of the pure “gender effect,” but this study emphasizes that such estimates do not capture the full extent of the wage disadvantages faced by females.
The main focus of this study is, within a matching framework, to examine the important interactions between gender and other relevant characteristics. Union membership and part-time work are two of these. The study also considers the effects of parenthood, age, and gender segregation. An important part of the approach taken is the inverse probability weighted regression adjustment (IPWRA) matching estimator. There are important statistical advantages from using an IPWRA estimator (mainly its “double robustness” property), but the key reason for using IPWRA is behavioral more than statistical. The IPWRA estimator can work with two treatment effects and hence estimate the effects of interactions between gender and another variable. For example, consider female and part-time as treatment variables. The IPWRA approach can simultaneously give the following treatment effects on hourly wages: (a) being female, (b) working part time, and (c) both being female and working part time (an interaction effect).
The conceptual relevance of these interactions is not new in the literature, as Blau and Kahn (2017) make clear, but such interaction effects have not previously been formally estimated in a consistent manner, if at all. The contribution of the paper is to provide clear evidence that a basic matching estimate of the gender pay gap is useful but does not tell the whole story. An analysis which includes not just a “gender only” effect on wages but also interactions between this gender effect and other key covariates (such as part-time work) is a much richer one. This is the main contribution of the study.
Section 2 provides a review of the literature. The data used by the study, which are two samples taken from the US Current Population Survey (CPS) for the period October 2011 to March 2012 and for the period October 2017 to March 2018, are described in Section 3, and the methodological approach is described in Section 4. The matching analysis with a single treatment effect is presented in Section 5 and the IPWRA analysis in Section 6. Section 7 presents the conclusions of the study.
2 Review of literature
Blau and Kahn (2017) present a comprehensive review of what is now an extensive literature on the gender pay gap in the USA. A number of themes arising in this literature are developed further in this paper. Blau and Kahn (2017) present detailed empirical evidence to show that some of the core issues have changed since the 1970s. Several of these are of particular relevance for this paper. Firstly, the gender wage gap has fallen dramatically but still remains sizeable. This is perhaps surprising given that the gap in education has been reversed in favor of women. They find that the gender wage gap has fallen from about 36–38% in 1970 to between 18 and 21% in 2010. The analysis presented in this study does not consider long-term changes but does confirm that a substantial wage gap remains.
In their meta-analysis of a total of 263 papers, Weichselbaumer and Winter-Ebmer (2005) also find evidence of a global reduction of the gender wage gap. At the same time that the gender wage gap was narrowing, the human capital factors used to explain the gap (education and actual work experience) were either moving in favor of women or strongly declining. Beaudry and Lewis (2014) associate the declining gender wage gap in the USA with changes in the price of skills, related to skill-biased technical change. In another US study, Borghans et al. (2014) find the decline in the gender wage gap to be associated with a growth in the importance of people skills. In a rare natural experiment, Flory et al. (2014) link the gap in gender wages to female aversion to competitive work environments.
Blau and Kahn (2017) report that the gender gap in years of education has reversed from − 0.2 to + 0.2 between 1981 and 2011 for the USA. The gap in years of work experience fell from 7 in 1981 to 1.4 years in 2011. In consequence, the role of these traditional factors in the gender wage gap has shrunk. Together, education and work experience explained about 27% of the gap in 1981 but only around 8% in 2010. A number of other explanatory factors have also reduced in significance, such as the effect of unionization on male wages. Despite this decline, the evidence presented in this study shows that unionization still plays a part in gender wage differences. Blau and Kahn (2017) show that, in contrast, some other factors have become increasingly important. For example, they find that gender segregation by occupation and industry has become of much greater consequence—accounting for only about 27% of the gap in 1980 but about 49% in 2010. The role of gender segregation is another theme which this study seeks to develop further.
The link between gender segregation and the gender wage gap has long since been made. Polachek (1981) constructs a model in which female earnings potential depreciates during temporary exits from the labor force while males remaining in the labor force see their earnings potential appreciate from continued skill development. The expectation of interruptions to work experience affects female investment in skills and, hence, occupational choice. Maternity drives women to self-segregate into jobs which are less innovative and less skill driven—occupations that tend to be paid less. Cobb-Clark and Moschion (2017) provide evidence from Australia that gender differences in educational performance exist at an early stage and vary according to socio-economic status.
A number of studies have tried to assess the extent of occupational segregation in the USA and elsewhere by means of the Duncan and Duncan (1955) segregation index. Blau and Kahn (2013a, b) find that the segregation index fell from 64.5 in 1970 to 51.0 in 2009. The decline was more rapid in the 1970s than in the 1980s and even more gradual in the following years. As Blau and Kahn (2017) note, even the diminished value of 51% still represents a high degree of occupational segregation. Unsurprisingly (given the known role that segregation has in explaining the gender wage gap), the high value of the segregation index relative to 2009 confirms that occupational and industry differences by gender still remain sizeable. This study also reports gender segregation indices for the USA with similar findings.
Hegewisch et al. (2010) find similar evidence of a declining degree of segregation in the USA. Moreover, they link gender segregation to the gender wage gap, finding a negative relationship between the share of women in employment in an occupation and the gender wage gap. Tomaskovic-Devey and Skaggs (2002) also link gender segregation to the gender wage gap, finding further evidence of the role of industries as a source of wage inequality. Levanon et al. (2009) consider the view that gender segregation and the gender wage gap are causally related by two sociological processes—devaluation and queuing—using US Census data. Their analysis found some evidence of devaluation (valuing the work of females less) but little evidence of queuing (employers preferring to hire males).
Other studies drew similar conclusions to the USA for other countries. For instance, Barón and Cobb-Clark (2010) find an important effect of occupational segregation on the gender wage gap in Australia. They find the gender wage gap to be fully explained by productivity characteristics but not fully explained for high-wage workers. Olsen and Walby (2004) find evidence from the UK that labor market rigidities—including the segregation of women into certain occupations and into smaller, non-unionized firms—were responsible for about 36% of the gender wage gap. Walby and Olsen (2002) also find both occupational and industrial segregation to have been prevalent in the UK. Livanos and Pouliakas (2012), in a study of Greece, find that gender segregation with respect to educational subject explained part of the gender wage gap. Pastore and Verashchagina (2011) find that the gender wage gap more than doubled during the transition from plan to market in Belarus, particularly because women have experienced increasing segregation in low-wage industries.
Polachek (1985) further extends this link between gender wages and a life cycle view of occupational choice. Polachek (2014) finds the gender pay gap to be smaller between single men and women and larger between married men and women. This is attributable to his life cycle model of human capital and the resulting different occupational structures between the genders. To the extent that educational choices by women are related to eventual occupational choices, the study of Danish labor markets by Humlum et al. (2019) suggests that these may also be affected by parental attitudes to labor markets. The role of maternity and aging on female earnings is confirmed by a comparatively recent strand of the literature which focuses on the labor market behavior of young people to try to ascertain at which stage the gender pay gap first arises. Many studies have found little or no gender wage gap among young people. A gap emerges after maternity and widens as workers age. Manning and Swaffield (2008) provide an early study of this type for the UK. In a study of US MBAs, Bertrand et al. (2010) attribute a growing gender wage gap that increased with age to career interruptions as well as differences in training and weekly hours of work. More recently, similar findings have been noted for several developing countries—see, for example, Pastore (2010) and Pastore et al. (2016). This study provides recent evidence for the USA which confirms the existence of much narrower differences in gender wages for younger than older workers.
Some research has been aimed at locating the gap along the earning distribution to understand whether it is generalized or whether it is attributable to particular groups of individuals with specific skill levels. Blau and Kahn (1997) find increased demand for highly skilled workers to have widened the gender wage gap. In their study covering 11 countries, Arulampalam et al. (2007) find evidence of a tendency for the gender pay gap to be concentrated mainly among the low-skill (so-called sticky floor effect) and the high-skill (so-called glass ceiling effect) workers. Examples of the latter include managerial positions, particularly senior management, and many highly paid liberal professions (Goldin, 2014). In these types of jobs, not only education and human capital are of importance but also relationships of trust with customers. This makes the role of some individuals hard to substitute and, in consequence, requires flexibility with respect to hours of work—conditions that are often not easily met by women. Olivetti (2006) provides a new measure of the returns to work experience, using PSID data for the USA. Her analysis shows that there has been a convergence in the rate of returns to work experience by gender, with female returns increasing more rapidly than those of men. This is attributed to the diffusion of new technologies that favor the skills of women more than those of men.
Sulis (2012), in a study of Italy, found that search frictions, productivity, and discrimination all shaped the gender wage gap. Another issue related to maternity is the prevalence of part-time working by women. Part-time working attracts lower hourly rates of pay and has often been identified as an important contributor to the gender wage gap. Blau et al. (2013) found that US policies encouraged women to undertake part-time work in lower level jobs. Ermisch and Wright (1993) provide evidence that women in the UK received lower wages in part-time than in full-time work. Moreover, as noted above, Goldin (2014) emphasizes the role of flexible working times in highly paid occupations and senior positions. This, in turn, is an argument to support the view that the preference of women for part-time work might tend to exclude women from such types of jobs. The role of part-time working in creating gender wage differences is another focal point of the analysis presented in this study.
Several studies have tried to understand the origins of discrimination and have found evidence that they are related to the persistence of traditional views regarding the gender division of roles in society. Fortin (2005) finds perceptions of the role of women in the home and in society to have a significant effect on the gender wage gap—that anti-egalitarian views are associated with a higher gender wage inequality. Pastore and Tenaglia (2013) find evidence of the role that different religious denominations have in favoring or hindering female employment—as a consequence of a different degree of secularization and of views regarding traditional gender roles and the male breadwinner family model.
Gauchat et al. (2012) examine other potential effects on gender wage inequality in the USA, such as the effects of globalization, finding that it contributes to a reduced gender pay gap. Oostendorp (2009) finds evidence that the occupational gender wage gap tends to decrease with respect to trade and foreign direct investment in richer countries but found little evidence of any effect in poorer countries. In a study of wages in India, Menon and Van der Meulen Rodgers (2009) even find the gender wage gap to increase with respect to openness to international trade.
All of the key themes developed by this paper have been previously considered in one way or another by the existing literature. At the heart of the gender pay gap is a sense that women are paid less than men for undertaking essentially the same work. Matching techniques offer the opportunity to better compare like with like, and such comparisons are of considerable importance. But the literature makes clear that female employment is typically not like male employment. For example, gender segregation, part-time working, parenthood, and unionization are all factors which affect differences between male and female wages. The contribution of this paper is to provide systematic and robust evidence on how these factors interact with the core “like for like” gender pay gap. It finds, for example, that being both a female and a part-time worker results in a much greater disadvantage in hourly wages than just being female. In so doing, it implies that the concept of a single gender pay gap is a too simplistic representation of reality.
3 Data
3.1 Data overview
The study uses two cross-section samples taken from the monthly US Current Population Survey (CPS), the first for October 2011 to March 2012 and the second for October 2017 to March 2018. Since both cross-sections comprise different individuals, it is not possible to formally test for changes between the two periods, but the intention was to check whether key conclusions change between the two periods. The full number of observations for the first sample was 907,775 and for the second 877,776. This sample includes non-responses and individuals who were not in employment at the time. For much of the analysis, the effective sample was necessarily limited to those individuals for whom sufficient information to obtain their usual hourly earnings existed. This amounted to 77,097 individuals for the first sample and 76,308 for the second. It should also be noted that the Stata software automatically removes observations for which there are missing values so the actual number of observations used in any one task may vary from these totals. The first sample (October 2011 to March 2012) comprised 51.6% females and 48.4% males, and the second sample (October 2017 to March 2018) had exactly the same proportions.
3.2 Sample characteristics
Table 1 provides employment rates of males and females for both samples. Participation rates for both males and females increased in the six years between the two samples. In both cases, the proportion of females not in the labor force was about 10% higher than that of males. Lower overall participation rates for females were not the only key difference from males. In both samples, the proportion of females working part time was substantially higher than that of males. In the second later sample, this became more exaggerated with the proportion of females engaged in part-time work being roughly double compared with that of males.
As Blau and Kahn (2017) note, the existence of gender segregation implies that industry and occupational differences between male and female employment are important contributory factors to gender differences in wages. To assess the extent and evolution of gender segregation, Table 2 reports gender segregation indices for CPS data over a much longer period (March 2005 to March 2018) than those used for the rest of the study. These indices suggest a gradual decline in gender segregation by occupation between March 2005 and March 2018, but the overall degree of segregation by the end still remained substantial. For segregation by industry, there is very little evidence of longer term change. Segregation by industry is lower than that by occupation but still of consequence. It is worth noting carefully that the values of gender segregation indices are necessarily affected by how both “occupation” and “industry” are defined. The narrower the definitions, the more likely one is to observe a greater degree of gender segregation.
These findings are consistent with other studies of gender segregation in US labor markets. Most notably, Blau et al. (2013) find a value of 51% for occupational segregation in 2009 compared with about 52% in March and September 2009 in this study. The results are also consistent with the findings of Hegewisch et al. (2010) on occupational segregation. The findings support the view of Blau and Kahn (2017) that the decline in gender segregation observed in earlier decades has stalled at levels that still represent a high degree of occupational segregation. Available existing evidence on segregation by industry is much more limited so providing such evidence is one of the contributions of this study.
The analysis necessarily used the CPS definitions of both occupation and industry. Detailed definitions of both industry and occupation were used. Due to changes in definitions over the period, the precise number of each varied, but there were at least 600 occupation and 250 industry categories included throughout. It is recognized that such definitions can never be wholly satisfactory and that the results could have been significantly affected by a different alternative set of definitions.
Another relevant feature of the data is that women exhibited lower rates of unionization than men. In the first sample (October 2011 to March 2012), 12.8% of males and 11.4% of females were unionized. In the second sample (October 2017 to March 2018), the comparable proportions were 11.0% for males and 9.9% for females.
3.3 Variables
Much of the analysis was concerned with the effect of gender on wages. For this, the outcome (dependent) variable was the lhwage, the log of usual hourly earnings. For most of the analysis, the key treatment variable was female (0 if male, 1 if female).
The following variables were used mainly as covariates but also served as treatment variables in some instances:
-
parttime, 0 if full time and 1 if part time
-
young, 0 if 25 or over and 1 if under 25
-
parent, 1 if a parent of a child aged under 18 but 0 if not
-
union, 1 if a union member but 0 if not.
The following variables were used as covariates only:
-
age
-
married, 1 if married but 0 if not
-
edyears, number of years of education
-
hours, the usual number of weekly hours worked
-
exper, expected experience (explained further below)
-
migrant, 0 if born in the USA but 1 if not
-
regional dummy variables
-
dummy variables for race
-
occupational dummy variables
-
sector dummy variables.
Both the occupational and sector dummies used the standard CPS definitions. It is recognized that occupations and industries are impossible to define in a wholly satisfactory way and that variations in these definitions could result in quite results for these dummy variables.
To calculate expected experience for each individual in the model, a probit model was used to estimate (separately) the probability of employment at each age starting at 15 and ending at 65. The role of expected experience (and of gender differences in the effect of parenthood) as a determinant of the gender pay gap was first advanced by Polachek (1975). In this paper, the model of expected experience was of the general form:
where empl is the (0, 1) variable for whether the individual was employed and D is a vector of regional and race dummy variables.
The marginal effects (probabilities) were then used to calculate the probability that each individual would have been in employment at each age from 15 to 65. These were then added together to give the expected experience in years. Given space constraints, the results are not reported here but are available from the authors on request.
4 Methodology
4.1 Wage decompositions using recentered influence functions
Firpo et al. (2018) offer an extension of the Oaxaca-Blinder wage decomposition using recentered influence functions (RIF). The technique involves two steps, the first of which is to divide the wage distribution into a composition and structure effect using a reweighted procedure (where the weights are estimated). The second step estimates structure and composition effects for each covariate; essentially in a manner similar to that of Oaxaca-Blinder. The key difference is that, using the method developed by Firpo et al. (2009) and Fortin et al. (2011), the dependent variable of the regression is replaced by the appropriate RIF. To implement this procedure, we used the oaxaca_rif routine in Stata.
Authors using different data sets than those of this study have used Oaxaca RIF decompositions to estimate the gender pay gap. Some of these, such as Kassenboehmer and Sinning (2014) and Töpfer (2017), found a high proportion of unexplained gender differences which they attributed to heterogeneity in their data. Wage decompositions were not a focus of this study. Our main purpose in producing such estimates was to demonstrate that similar problems existed with the two data sets used for this study. The evidence that similar issues exist with the CPS data is intended to support the use of matching estimators in this study. A summary of the results of the Oaxaca RIF analysis is presented in the Appendix. More detailed results are available from the authors on request. The interpretation of the results needs some care. In particular, the “unexplained” component is open to misinterpretation and differing points of view. Further details are not provided here since this study argues that a different methodological approach is more suited to its topic.
4.2 Matching with a single treatment variable
The existing empirical literature emphasizes the need to compare like with like with respect to gender pay differences. Some authors, including Ñopo (2008) and Frölich (2007), have advocated the use of matching estimators for this purpose. Both authors propose these techniques as an alternative to the decompositions of the type proposed by Blinder (1973) and Oaxaca (1973). For example, Ñopo (2008) argues that matching addresses the “out of support” problem inherent in Blinder-Oaxaca wage decomposition models. Section 4.1 above argued that a more modern version of wage decompositions using RIF is still subject to heterogeneity issues. Matching approaches are well equipped to deal with heterogeneity issues. In addition, the heart of the matching approach (the selection of a carefully matched control group) has considerable intuitive appeal in any attempt to compare like with like.
A matching approach starts by defining an outcome variable (log of hourly earnings) and a (0, 1) treatment variable (female). It seeks to establish whether a statistically significant difference exists in the log of hourly earnings between the treated (female) group and the untreated (male) group. The procedure selects a control group from the untreated (male) group which is selected to be, as far as possible, identical in all other relevant observable characteristics to the treated (female) group.
A key issue for all matching techniques is the “missing data” problem. For example, the treatment variable (say being female) is observed, but, to compare male and female wages accurately, we would need to know what would have happened if the same individual had been born male. This clearly cannot be observed, and the “missing data” problem is how best to replicate it from an appropriate counterfactual. With a single treatment variable, this means selecting an appropriate control group.
This study uses three different approaches to the selection of the control group. These are propensity score (PS) matching (using kernel density matching), matching by Mahalanobis distance, and coarsened exact matching (CEM). Given the widespread use of the first two matching techniques in the literature, no further explanation is offered here. The CEM technique is a more recent addition to the matching toolbox: see Iacus et al. (2012). For matching by both propensity score and by Mahalanobis distance, the treated group is not changed and the only “matching” occurs in the creation of a control group. With coarsened exact matching, the process excludes all those observations from the treated group for which a nearly exact match on all covariates cannot be found. CEM sets a maximum difference in the covariates between the treated and untreated groups and removes observations from both groups where no nearly exact match exists. In many respects, this makes it a more rigorous attempt to compare like with like, but, unlike the other approaches, it results in sample size reductions.
Neither PS nor Mahalanobis matching techniques remove those observations from the treated group that are “difficult” to match closely. In consequence, an issue arises of how closely the control group matches the treated group (sometimes referred to as “bias on observables”). For each analysis using both techniques, the match between the two groups was checked using the psmatch2 routine in Stata. The resulting graphs are reported in the separate appendices available from https://www.researchgate.net/publication/331703104_Meara_Pastore_Webster_specification_checks.
A further more intractable problem is the risk of bias on unobservables: an excluded confounding variable may have biased the results. This study uses a large number of covariates in the treatment model in an attempt to reduce this risk (see Section 3). However, as King and Nielsen (2016) have pointed out, doing this can create a risk of a different form of bias: from matching on irrelevant variables. To limit that risk, all covariates included in the probit (treatment) model were first tested for statistical significance in a regression model with the outcome as the dependent variable. These regressions are not reported but details are available from the authors on request.
The approach taken in this study reflects conceptual as well as statistical issues. For matching estimators to be unbiased, they need to include all relevant observables. This means that in estimating the gender pay gap, the technique should control for other covariates that are known to also affect the difference in gender wages. These include the effects of gender segregation, part-time working, unionization, and parenthood. It is, of course, central to the study to estimate the gender wage gap on as close to a “like for like” basis as possible. However, it is also important to recognize that this is an estimate of the direct consequence of gender on wages and that there are other less direct mechanisms that affect gender wages. The approach of this study is to identify how the gender pay gap changes when these “indirect” effects of being female are taken into account.
The CPS data reveal, as expected, that part-time working is more common among females than males and that females are less unionized. The study first uses matching to show that, with the CPS data, there existed a union wage premium and an hourly wage discount for working part time. Next, the study estimated the core (like for like) gender pay gap for both samples. This is estimated firstly with industry and occupation dummies. It was then re-estimated without these dummy variables to identify the effect of gender segregation on the gender pay gap. For the remainder of the matching analysis, the sample was sub-divided into two according to one of the key covariates. These were used to show how the gender pay gap varies between one group and another. For example, the sample was divided into young (under 25) and older workers and the gender pay gap estimated for each. A similar approach was taken for part-time working, union membership, and parenthood. These provided a key insight into how each of these variables influences differences in gender wages.
4.3 Matching with inverse probability weighted regression adjustment (IPWRA)
The IPWRA estimator derived by Cattaneo (2010) and Cattaneo et al. (2013) differs from most matching estimators in that it estimates both a treatment model and an outcome model. The treatment model is similar to most matching models. It estimates the probability of the treatment variable (female in this case) being associated with each of a number of characteristics. Many matching models use probit for this purpose. In this study, the IPWRA treatment model used a logit model.
The treatment model gives the probability of, say, observing a female given that one observes a part-time worker. That is, the treatment model is used to assign a sampling probability for each observation. The inverse of this probability is then used to weight each observation in the outcome models. The inverse probabilities are used to address the “missing data” problem. Using these inverse probabilities, in essence, creates a counterfactual to address the missing data issue. The technique next estimates a number of (inverse probability) weighted regression outcome models, one for each treatment level. Each of these produces a series of treatment-specific predicted outcomes, one for each treatment level. The means of these predicted outcomes are then used to estimate the treatment effect.
The IPWRA estimator can be shown to have some important statistical properties. The most important of these is the property of “double robustness”: see Cattaneo (2010) and Cattaneo et al. (2013). That is, if either the treatment model or the outcome model is incorrectly specified but the other is correctly specified, then the estimates are still consistent. This means that it is only necessary for one of the two to be correctly specified for the estimator to be consistent. As a corollary, it is necessary to assume that at least one of the treatment or outcome models does not exclude a confounding variable.
Hirano et al. (2003) have shown that doubly robust estimators (which include IPWRA) exhibit a lower bias than estimators without the double robustness property. Another common problem with matching models is mis-matching on irrelevant variables. King and Nielsen (2016) point out that IPWRA estimators are less prone to mis-matching on irrelevant observables.
From the perspective of this paper, the reasons for using the IPWRA are not just for the desirable statistical properties of the estimator but also for the questions that it can address. The model is specified to work with a number of discrete treatment levels. This means that it can be adapted to work with more than one treatment variable. For example, suppose that that we have two (0, 1) treatment variables: female and parttime. This can be adapted into four treatment levels:
-
Treatment level 0: female = 0 and parttime = 0
-
Treatment level 1: female = 1 and parttime = 0
-
Treatment level 2: female = 0 and parttime = 1
-
Treatment level 3: female = 1 and parttime = 1
In this way, it is possible to use the IPWRA to estimate both treatment effects separately and to estimate their joint (interaction) effect when both apply. It is this feature that makes it particularly useful for analyzing the interaction between gender and other related influences such as part-time working, unionization, and parenthood.
In this study, the outcome variable for all IPWRA models was the log of hourly wages. For both the treatment and outcome models, the full set of covariates listed in the preceding section was used. An important assumption of the IPWRA model is known as the overlap assumption. This means that every individual must have a positive probability of receiving each treatment level. For example, it must be possible that union members can be male and can be female. If unions excluded all males or all females, the overlap assumption would be violated. Stata produces graphical checks for the overlap assumption. These are not reported for the IPWRA models in Section 6 but are available in separate appendices available from https://www.researchgate.net/publication/331703104_Meara_Pastore_Webster_specification_checks.
Finally, as with other matching models, the IPWRA analysis assumes that treatments and outcomes are statistically independent (conditional mean independence).
4.4 Interpretation of results
For both the single treatment and the IPWRA matching analysis, the outcome variable is the log of hourly wages. Consequently, the average treatment effect on the treated (ATT) is the difference in the log of wages between, say, females and males. This is often interpreted as the percentage difference in wages. However, the difference in logs is only a linear approximation (by means of a Taylor expansion) of the true percentage difference. This approximation (as can be seen in our results) is only accurate when the difference between the two sets of wages is small. Since the precise percentage difference can readily be derived from the matching output, this is reported together with the relevant ATT throughout this paper, except for the CEM analysis (for which the ATT is estimated differently and correctly reflects the exact percentage difference).
5 Matching analysis with a single treatment variable
5.1 Treatment effects of part-time working and union membership
This section provides a supporting analysis for work to follow on the gender pay gap. Earlier analysis of the CPS data (Section 3) has shown that women are less likely than men to be unionized but more likely to be working part time. The purpose of this analysis is to demonstrate that, with the CPS data, both union membership and part-time working have significant effects on wages in their own right.
Table 3 presents matching estimates of the reduction in hourly wages from working part time and the wage premium from being a union member. These are for the full sample and made use of the full set of covariates listed in Section 4 earlier, including industry, occupation, race, and region dummies. Results are for propensity score (kernel density) matching and use a second set of estimates (from matching by Mahalanobis distance) as a robustness check. Since this is a supporting analysis, we do not also provide a set of CEM estimates (as is done with later analysis) in the interests of being concise.
Table 3 shows a statistically significant premium for union membership according to the PS matching estimator. The results (statistically significant at 99% confidence) imply a union wage premium of about 14% for our first sample and about 13% for the second. The Mahalanobis estimates for the first sample are comparable with those of the PS estimator for the first sample (a premium of about 14%) but slightly lower for the second sample (a premium of about 11%). Both estimators support a substantial and statistically significant union wage premium in each sample.
For part-time working, our results consistently show a substantial and statistically significantly lower hourly wage than for full-time working. Propensity score estimates for both our samples are comparable: a part-time discount of about 19% in October 2011 to March 2012 and of about 21% in October 2017 to March 2018. Estimates for matching by Mahalanobis distance are again comparable across the two samples—discounts of about 14% and 16%—but are somewhat lower than those for the propensity score estimator. Nonetheless, both estimators support a conclusion that a substantial disadvantage in hourly wages exists from working on a part-time basis.
This study reported earlier that, for our samples from the US CPS data, women were more likely to work part time and less likely to be unionized. The analysis in this section has shown that, for the same data, both characteristics would contribute to an overall difference between male and female wages that goes beyond the impact of the direct effect of gender alone. This is a key point to be explored further in this study. It implies that a “like for like” comparison of the direct effect of gender on wages is not the only effect that merits consideration.
5.2 Treatment effects of gender
This section focuses on matching estimates for the gender pay gap in the US using both our samples. As discussed earlier, it is important that the matching process makes use of all relevant observed covariates. Not to do so would expose the estimates to an increased risk of bias on unobservables. The resulting estimate is, in consequence, an estimate of the effect on wages of being female with the effects of all other observed covariates controlled by the matching process. Such estimates are unquestionably useful but give rise to two sets of concerns. These are not really statistical but are important for our understanding of gender wage differences. Firstly, we know from the literature that gender wage differences can vary by, for example, age group and that gender segregation affects gender wage differences. It is important to understand these factors. Secondly, the process of matching selects controls (males) which are similar in terms of, say, parenthood, part-time working, or union membership. All of these can affect gender wage differences. In short, there needs to be an estimate of the effect of gender on wages where, as far as possible, like is compared with like. But in so doing, it is important not to neglect other more indirect routes by which gender wage differences occur.
In this section we start by estimating the gender pay gap for both our samples. The main estimate of the gender pay pap quite properly controls for the effect on wages of the concentration of women in lower paid occupations or industries (gender segregation). To identify the effects of gender segregation, we repeat the analysis but without industry or sector dummy variables. Next, we consider the effect of age on the gender wage differences by applying our matching estimates to two sub-samples—young (under 25) and older. Since part-time working results in lower hourly wages (see the preceding section), we then estimate separate gender wage gaps for part-time and full-time workers. Separate gender pay gaps are then estimated for parents and non-parents and for union members and non-members. The purpose of all of these is to provide a much richer analysis and interpretation than just the direct effect of gender on wages.
Table 4 reports the results of this analysis using propensity score (PS) matching (kernel density), Table 5 repeats the analysis for matching by Mahalanobis distance, and Table 6 also repeats the analysis using coarsened exact matching (CEM). The PS matching (Table 4) is included since it is the most widely understood matching technique. Matching by Mahalanobis distance (Table 5) and matching by the CEM technique (Table 6) are both included as robustness checks on the findings of the PS matching analysis.
The PS matching analysis (Table 4) produced an estimate of a statistically significant gender pay gap of about 13% for the October 2011 to March 2012 sample and of about 12% for the October 2017 to March 2018 sample. Comparable estimates using (a) Mahalanobis distance (Table 5) and (b) CEM (Table 6) were (a) 13% and 10.5% and (b) 12% and 14%. In all cases, these estimates were statistically significant at 99% confidence. These estimates represent the gender pay gap resulting from the direct effect of being female. That is, the secondary effects of, for example, part-time working, parenthood, or union membership are included in the controls and not in the estimate.
Table 4 shows the effect of taking into account gender segregation by means of industry and occupation dummy variables. Removing these industry and occupation dummies increased the estimate of the gender pay gap to 15% for the first sample and to 16% for the second. A comparable effect was observed with both the Mahalanobis and CEM estimators (Tables 5 and 6). Interpretation of these findings is important. It is not necessary to choose between estimates with industry and occupation dummy variables and those without. Both convey complementary information. To the extent to which the matching was successful in comparing like with like, the estimates for, say, the second sample showed that being female involved hourly wages that were typically 13% less than those for males. Since this estimate controls for differences in industry and occupation, it does not take into account gender segregation. When we allow for the effects of females being more concentrated in lower paid industries and occupations, the comparable estimate is a pay gap of 17%. As with Blau and Kahn (2017), this supports the conclusion that gender segregation by industry and by occupation is important in understanding gender wage differences.
The next sub-division of the sample was between young (under 25) and older. Previous studies have found the gender pay gap to be smaller or even non-existent for younger workers. With the PS matching (Table 4), this study finds a small but statistically significant gender pay gap for young individuals, of about 2% in our first sample and about 3% in the second. Both the Mahalanobis distance matching (Table 5) and the CEM (Table 6) analysis found no statistically significant gender pay differences (at 95% confidence) for young workers. These findings contrast sharply for the estimates of the gender pay gap for older workers. For each of the three estimators, these were statistically significant and substantially higher than those for young workers. The PS matching estimates (Table 4) imply a gender pay gap of about 13% for older workers in the first sample and of about 14% in the second sample. Mahalanobis distance (Table 5) and CEM (Table 6) yield similar results. The sharp difference in the gender pay gap between young and older workers has some obvious potential implications for the role of marriage and parenthood in gender pay differences. These are discussed further later.
Sub-dividing the sample by part-time and full-time workers produces some further interesting findings. The PS matching analysis (Table 4) suggests a statistically significant but small gender pay gap for part-time workers. For this first sample, this was estimated at 3% and, for the second sample, 6%. Both Mahalanobis and CEM techniques (Tables 5 and 6) found no statistically significant (at 95%) gender pay difference between male and female part-time workers. The gender pay gap for full-time workers estimated by PS matching (Table 4) was statistically significant and substantial for both samples—14% for the first sample and 15% for the second. Both Mahalanobis and CEM techniques produced similar estimates (Tables 5 and 6). The finding of no statistically significant gender difference in the hourly wages of part-time workers is of consequence. Evidence presented earlier shows both that a higher proportion of females than males work part time and that part-time working involves its own gap in hourly pay relative to full time. That there is little or no gender pay difference between male and female part-time workers implies that the interaction between gender and part-time effects is of importance. That is, the role of part-time working in the gender pay gap is more through the pay disadvantage of part-time working than any significant gender wage difference between part-time workers. This is further analyzed in the next section.
The division of both samples by parenthood finds a statistically significant gender pay gap for both parents (of children under 18) and for non-parents in both samples, according to all three of the matching estimators used. In every case, the estimated wage gap for parents was substantially greater than that for non-parents. For example, the estimated wage gap for parents using PS matching was about 17% in the first sample and about 18% in the second sample. The comparable estimates for non-parents were 10% and 12%. These findings complement those with respect to age, which imply changes in the gender pay gap at ages consistent with parenthood. They also complement the existing literature which finds a role for parenthood affecting the gender pay gap, not least through its impact on experience and human capital. Again, the role of parenthood is further analyzed in the next section.
The last sub-division of the samples was with respect to union membership. Again all three matching estimators find a statistically significant gender pay gap for both samples and for both union and non-union members. In almost all cases, the estimated gender pay gap for union members is greater than that for non-members. With PS matching, the gender pay gap for union members in the first sample was estimated at about 12% and for non-members at 11%. For the second sample, the comparable estimates were 16% and 13%. These findings imply a contradictory effect of union membership on gender wages. Union membership, as shown earlier, involves a wage premium which, given low female unionization, should widen the gender pay gap. In contrast, the gender pay gap not only exists between male and female union members but also is higher than that for those who are not unionized. This implies that to fully understand the net overall effect of the interaction between unionization and gender on pay, further analysis is needed. This is provided in the next section.
6 IPWRA analysis for the full sample
6.1 With gender and part-time working as treatments
Table 7 presents the results of the IPWRA analysis with both female and parttime as treatment variables. The two treatment variables were combined to produce the following composite treatment levels:
-
Treatment level 0—male full time (female = 0 and parttime = 0)
-
Treatment level 1—female full time (female = 1 and parttime = 0)
-
Treatment level 2—male part time (female = 0 and parttime = 1)
-
Treatment level 3—both female and part time (female = 1 and parttime = 1)
The results are divided into two parts—absolute and relative treatment effects. Absolute effects are the treatment effects where the control group is treatment level 0 (comparable male full-time workers). Relative effects compare the other (non-zero) treatment levels with each other. In particular, treatment effects were estimated for:
-
(a)
Treatment level 1 (female full time) relative to treatment level 2 (male part time)
-
(b)
Treatment level 1 (female full time) relative to treatment level 3 (female part time)
-
(c)
Treatment level 2 (male part time) relative to treatment level 3 (female part time).
In a similar manner to the earlier matching analysis, the full set of variables listed in Section 4 was used to construct the relevant treatment and outcome models in each case.
The absolute effects presented in Table 7 produce some interesting findings. Firstly, the gender pay gap between male and female full-time workers was 14% in both the earlier and later of the two samples. These are values consistent with the earlier matching analysis. Secondly, the analysis confirms a substantial gap in hourly pay rates between part-time and full-time workers. The gap in hourly pay between full-time and part-time males was about 24% in both samples. This confirms the earlier findings that part-time working involves a substantial disadvantage in hourly pay rates relative to full-time working. Lastly, the (separate) pay gaps for being female and for working part time re-enforce each other when it comes to the pay gap between part-time women and full-time men. For the earlier sample, this estimated gap in pay was about 27% and for the later sample approximately 28%. This provides clear evidence that the prevalence of part-time working is an important mechanism by which the “like for like” gender pay gap is worsened. That is, it shows that the wage disadvantage of being female is substantially worsened when the prevalence of female part-time working is taken into account.
For the relative effects, female part-time working was found to result in substantially lower hourly wages compared with all female workers. This gap was found to be about 15% in the earlier sample and 16.5% in the later one. This provides evidence that the gap between part-time and full-time rates exists for females as well as for males. Female part-time workers were also found to have statistically significantly lower hourly wages than comparable part-time workers of both genders. However, the gender pay gap among part-time workers was comparatively modest—about 3% in both samples. Finally, part-time males were found to have substantially lower wages than females (both part and full time). This implies that the wage disadvantage of working part time is larger than the disadvantage from being female. This finding emphasizes the importance of including the wage disadvantages of part-time working within the understanding of gender wage differences.
The outcome of the IPWRA analysis of gender and part-time working performs two key functions. Firstly, it shows that the disadvantages of working part time and the prevalence of part-time working among females are both relevant and important for understanding gender wage differences. Secondly, it provides a robustness check on many of the earlier findings of the matching analysis. Since there are also no substantial behavioral differences between the two different time periods, the main findings are not just robust with respect to choice of estimator but also robust with respect to the choice between the two cross-sections.
6.2 With gender and union membership as treatments
Table 8 presents the results of the IPWRA analysis using both gender and unionization as treatments. The following composite treatment levels were used:
-
Treatment level 0—male non-union (female = 0 and union = 0)
-
Treatment level 1—female non-union (female = 1 and union = 0)
-
Treatment level 2—male union (female = 0 and union = 1)
-
Treatment level 3—both female and union (female = 1 and union = 1)
In this case, the absolute effects are the treatment effects in relation to the control group of non-union males (treatment level 0).
Relative effects compare:
-
(a)
Treatment level 1 (female non-union) with treatment level 2 (male union)
-
(b)
Treatment level 1 (female non-union) with treatment level 3 (female union)
-
(c)
Treatment level 2 (male union) with treatment level 3 (female union).
As before, the full set of variables listed in Section 4 was used to construct the relevant treatment and outcome models. These included industry and occupation dummy variables.
Table 8 finds a gender pay gap between non-unionized females and non-unionized males of about 14% in the earlier sample and around 15% in the later one. Again this is consistent with the preceding estimates of the “like for like” gender pay gap. The results also provide evidence of a substantial union wage premium. Male workers benefited from a union wage premium of approximately 18% in the October 2011 to March 2012 sample and of about 17% in the October 2017 to March 2018 sample. Relative to non-unionized males, the effect of female union membership was to reduce the gender pay gap to about 8% in the earlier sample and about 10% in the later sample. That is, the existence of a union wage premium helps to reduce the overall pay gap for females but does not eliminate it.
The relative treatment effects also produce some interesting and relevant findings. One of these is that there exists a gender pay gap within unionized labor. In the earlier sample, female union members were typically paid about 13% less than comparable males and in the later sample about 16% less. For women, as with men, the results show a union wage premium but this is smaller than that for males. The estimated female wage premium was 8.5% in the earlier sample and about 6% in the later one, both less than one half of the male union wage premium. The estimated gender pay gap between non-unionized females and unionized males is in the order of 40% for both samples.
As with part-time working, the IPWRA analysis shows that a strict “like for like” comparison between male and female wages ignores another indirect mechanism by which female wages are disadvantaged. For both male and female workers, there is a union wage premium, although the premium for women is lower. That females are less likely to be unionized also means that any given union wage premium does less to reduce the overall difference in gender wages. A combination of union premium and gender wage gap leads to very large differences in hourly pay rates between non-unionized females and unionized males.
6.3 With gender and parenthood as treatments
This analysis considers composite treatments derived from the two (0, 1) treatment variables female and parent. The following composite treatment levels were used:
-
Treatment level 0—male non-parent (female = 0 and parent = 0)
-
Treatment level 1—female non-parent (female = 1 and parent = 0)
-
Treatment level 2—male parent (female = 0 and parent = 1)
-
Treatment level 3—both female and parent (female = 1 and parent = 1)
Absolute treatment effects were in comparison to the control group of treatment level 0 (male non-parents).
Relative effects compare:
-
(a)
Treatment level 1 (female non-parent) with treatment level 3 (female parent)
-
(b)
Treatment level 1 (female non-parent) with treatment level 2 (female parent)
-
(c)
Treatment level 2 (male parent) with treatment level 3 (female parent).
Table 9 presents the results of this analysis. For non-parents, the core (“like for like”) gender pay gap was statistically significant in both the October 2011 to March 2012 and the October 2017 to March 2018 samples (about 10% in the first sample and about 11% in the second). The effect of being a male parent (relative to comparable male non-parents) was estimated to result in a statistically significant wage premium of about 8% in the first sample and about 3% in the second. The (absolute) effect of being both female and a parent implies a wage disadvantage of about 5% compared with male non-parents in the first sample and about 11% in the second.
The relative effects are of particular interest. For females, as with males, the results suggest that a statistically significant wage premium exists for parents in relation to non-parents. This premium was estimated at just under 4% for both samples. Within the sub-sample of all parents, the results show a substantial wage disadvantage from being a female parent (in relation to male parents). This disadvantage was estimated at 14.2% for the first sample and 14.7% for the second. Lastly, the results suggest that the effect of parenthood is to widen the gender pay gap. The estimated treatment effect (in relation to all females) of being a male parent implied a gender wage gap of about 22% in the October 2011 to March 2012 sample and of about 24% in the October 2017 to March 2018 sample.
The finding that parenthood is a further source of wage disadvantage for females is, perhaps, not surprising but important to be supported with evidence. These findings do, however, need careful interpretation. The data include only those females in employment at the time of the relevant surveys. The CPS data identifies parents of children under 18 years at the time of survey. This means that they are not capable of incorporating past adverse effects on human capital for those parents whose offspring are now adults. Despite these limitations, the analysis offers evidence which supports the existing literature which emphasizes the role of female parenthood in understanding the gender pay gap.
6.4 With gender and youth as treatments
Table 10 presents the IPWRA analysis which considers composite treatments derived from the treatment variables female and youth (defined as age under 25). The following composite treatment levels were defined:
-
Treatment level 0—older male (female = 0 and youth = 0)
-
Treatment level 1—older female (female = 1 and youth = 0)
-
Treatment level 2—young male (female = 0 and youth = 1)
-
Treatment level 3—young female (female = 1 and youth = 1)
Absolute treatment effects were in comparison to the control group of treatment level 0 (older males).
Relative effects compare:
-
a)
Treatment level 1 (older female) with treatment level 3 (young female)
-
b)
Treatment level 1 (older female) with treatment level 2 (young male)
-
c)
Treatment level 2 (young male) with treatment level 3 (young female).
The results presented in Table 10 imply a gender pay gap for those aged 25 or over of about 12% in the October 20011 to March 2012 sample and of 12.5% for the October 2017 to March 2018 sample. For those aged under 25 years, there was also a statistically significant gender pay gap but of much smaller magnitude. For both samples, this was estimated at approximately 3%.
For males, the effect of being young, unsurprisingly, results in statistically significantly lower hourly wages compared with being older. For the earlier sample, the gap was estimated at about 25% and for the later sample at about 22%. For females, the comparable effect was a gap of about 21% for the earlier sample and around 20% for the later one. Given that both being young and being female involve lower hourly wages, it is not wholly surprising that both effects re-enforce each other to create a substantial wage gap between young females and older males. For the earlier sample, this gap was estimated at about 27% and for the later sample at just over 25%.
7 Conclusions
The existing literature on the gender pay gap is extensive and the range of potential causes very numerous. This study has, for example, only touched on a sub-set of the wide range of issues covered by Blau and Kahn (2017). However, there remains a scope for formal statistical analysis. Not all relevant propositions have been tested. Estimations of the gender pay gap through Oaxaca RIF wage decompositions are still beset with concerns relating to the unexplained component and heterogeneity within the sample. Matching estimators provide a stronger basis for controlling for heterogeneity. In a sense, they provide more reassurance that the “unexplained” gender pay gap is in fact not explained by observable characteristics such as part-time working or parenthood.
Despite the strengths of a matching approach in controlling for covariates other than gender, it is too easy to overlook that some of these are also relevant to understanding gender wage differences. Part of the contribution of this study is that it does not ignore many of the more relevant covariates. It shows that when the concentration of women in lower paid occupations and industries (gender segregation) are taken into account, then the gender pay gap increases. It shows that the gap in hourly wages is much smaller for part-time than for full-time workers and for younger than for older workers and, in some cases, not even statistically significant.
The main contribution of this study is in looking at how these key mechanisms by which females are further disadvantaged interact with the gender effect itself. The IPWRA analysis estimates (for October 2017 to March 2018) a gender pay gap of about 15% and a gap in hourly wages from working part time (compared to full time) of about 27%. For those individuals who are both a female and a part-time worker, the gap compared with that for full-time males was estimated at 31%. This shows that part-time working has as important an effect on gender wage differences as the direct “like for like” gender effect.
The matching analysis also showed the gender pay gap for unionized workers to be higher than that for non-unionized workers. It also showed that unionized workers of both genders benefit from a union wage premium. The IPWRA analysis shows that the net effect of union membership is that female union members face a smaller gender pay gap than other workers. That is, despite the gender pay gap being greater for unionized females than for non-unionized females, the existence of the union wage premium means that they face a lower gender pay gap overall.
This paper used a matching approach to obtain as close as possible a “like for like” estimate of the gender pay gap and then examined how the gender pay gap changes with respect to other influences on gender wage differences such as gender segregation, part-time working, and low female unionization. The extensive literature on gender pay means that these have all been discussed somewhere previously. The contribution of this paper is to provide explicit, soundly based estimates of these interactions. This offers a much richer understanding of the way in which different sources of disadvantage for females interact in the creation of gender pay differences. In some instances, it implies that it might be better not to think of a single gender pay gap but of a series of different pay gaps for different groups.
References
Arulampalam W, Booth AL, Bryan ML (2007) Is there a glass ceiling over Europe? Exploring the gender pay gap across the wage distribution. ILR Rev 60(2):163–186
Barón JD, Cobb-Clark DA (2010) Occupational segregation and the gender wage gap in private-and public-sector employment: a distributional analysis*. Econ Record 86(273):227–246
Beaudry P, Lewis E (2014) Do male-female wage differentials reflect differences in the return to skill? Cross-city evidence from 1980-2000. Am Econ J Appl Econ 6(2):178–194
Bertrand M, Goldin C, Katz LF (2010) Dynamics of the gender gap for young professionals in the financial and corporate sectors. Am Econ J Appl Econ 2(3):228–255
Blau FD, Kahn LM (1997) Swimming upstream: trends in the gender wage differential in the 1980s. J Labor Econ 15:1–42
Blau FD, Kahn LM (2013a) The feasibility and importance of adding measures of actual experience to cross-sectional data collection. J Labor Econ 31(S1):S17–S58
Blau FD, Kahn LM (2013b) Female labor supply: why is the United States falling behind? Am Econ Rev 103(3):251–256
Blau FD, Kahn LM (2017) The gender wage gap: extent, trends, and explanations. J Econ Lit 55(3):789–865
Blau FD, Brummund P, Liu AYH (2013) Trends in occupational segregation by gender 1970–2009: adjusting for the impact of changes in the occupational coding system. Demography 50(2):471–492
Blinder AS (1973) Wage discrimination: reduced form and structural estimates. J Human Resour 436–455
Borghans L, Ter Weel B, Weinberg BA (2014) People skills and the labor-market outcomes of underrepresented groups. ILR Rev 67(2):287–334
Cattaneo MD (2010) Efficient semiparametric estimation of multi-valued treatment effects under ignorability. J Econ 155(2):138–154
Cattaneo MD, Drukker DM, Holland AD (2013) Estimation of multivalued treatment effects under conditional independence. Stata J 13(3):407–450
Cobb-Clark DA, Moschion J (2017) Gender gaps in early educational achievement. J Popul Econ 30:1093–1134
Duncan OD, Duncan B (1955) A methodological analysis of segregation indexes. Am Sociol Rev 20(2):210–217
Ermisch JF, Wright RE (1993) Wage offers and full-time and part-time employment by British women. J Hum Resour 28:111–133
Firpo S, Fortin NM, Lemieux T (2009) Unconditional quantile regressions. Econometrica 77(3):953–973
Firpo S, Fortin N, Lemieux T (2018) Decomposing wage distributions using recentered influence function regressions. Econometrics 6(2):28
Flory JA, Leibbrandt A, List JA (2014) Do competitive workplaces deter female workers? A large-scale natural field experiment on job entry decisions. Rev Econ Stud 82(1):122–155
Fortin NM (2005) Gender role attitudes and the labour-market outcomes of women across OECD countries. Oxf Rev Econ Policy 21(3):416–438
Fortin NM, Lemieux T, Firpo S (2011) Decomposition methods. In O. Ashenfelter and D. Card, eds., Handbook of labor economics, Vol. 4A, chap. 1, pp. 1 102. North-Holland, Amsterdam
Frölich M (2007) Propensity score matching without conditional independence assumption—with an application to the gender wage gap in the United Kingdom. Econ J 10(2):359–407
Gauchat G, Kelly M, Wallace M (2012) Occupational gender segregation, globalization, and gender earnings inequality in US metropolitan areas. Gend Soc 26(5):718–747
Goldin C (2014) A grand gender convergence: its last chapter. Am Econ Rev 104(4):1091–1119
Hegewisch A, Liepmann H, Hayes J, Hartmann H (2010) Separate and not equal? Gender segregation in the labor market and the gender wage gap. IWPR Briefing Paper, 377
Hirano K, Imbens GW, Ridder G (2003) Efficient estimation of average treatment effects using the estimated propensity score. Econometrica 71(4):1161–1189
Humlum MK, Nandrup AB, Smith N (2019) Closing or reproducing the gender gap? Parental transmission, social norms and education choice. J Popul Econ 32(2):455–500
Iacus SM, King G, Porro G (2012) Causal inference without balance checking: coarsened exact matching. Polit Anal 20(1):1–24
Kassenboehmer SC, Sinning MG (2014) Distributional changes in the gender wage gap. ILR Rev 67(2):335–361
King G, Nielsen R (2016) Why propensity scores should not be used for matching. Copy at http://j. mp/1sexgVw Download Citation BibTex Tagged XML Download Paper, 378
Levanon A, England P, Allison P (2009) Occupational feminization and pay: assessing causal dynamics using 1950–2000 US census data. Soc Forces 88(2):865–891
Livanos I, Pouliakas K (2012) Educational segregation and the gender wage gap in Greece. J Econ Stud 39(5):554–575
Manning A, Swaffield J (2008) The gender gap in early-career wage growth. Econ J 118(530):983–1024
Menon N, Van der Meulen Rodgers Y (2009) International trade and the gender wage gap: new evidence from India’s manufacturing sector. World Dev 37(5):965–981
Ñopo H (2008) Matching as a tool to decompose wage gaps. Rev Econ Stat 90(2):290–299
Oaxaca, R. (1973). Male-female wage differentials in urban labor markets. Int Econ Rev 693–709
Olivetti C (2006) Changes in women’s hours of market work: the role of returns to experience. Rev Econ Dyn 9(4):557–587
Olsen W, Walby S (2004) Modelling gender pay gaps. Equal Opportunities Commission, Manchester
Oostendorp RH (2009) Globalization and the gender wage gap. World Bank Econ Rev 23(1):141–161
Pastore F (2010) The gender gap in early career in Mongolia. Int J Manpow 31(2):188–207
Pastore F, Tenaglia S (2013) Ora et non Labora? A test of the impact of religion on female labor supply, IZA DP No 7356
Pastore F, Verashchagina A (2011) When does transition increase the gender wage gap? Econ Transit 19(2):333–369
Pastore F, Sattar S, Sinha N, Tiongson ER (2016) When do gender wage differences emerge? A study of Azerbaijan’s labor market. World Bank policy research working paper 7613
Polachek SW (1975) Potential biases in measuring male-female discrimination. J Hum Resour 10:205–229
Polachek SW (1981) Occupational self-selection: a human capital approach to sex differences in occupational structure. Rev Econ Stat 63:60–69
Polachek SW (1985) Occupation segregation: a defense of human capital predictions. J Hum Resour 20(3):437–440
Polachek SW (2014) Equal pay legislation and the gender wage gap. IZA World of Labor
Sulis G (2012) Gender wage differentials in Italy: a structural estimation approach. J Popul Econ 25(1):53–87
Tomaskovic-Devey D, Skaggs S (2002) Sex segregation, labor process organization, and gender earnings inequality. Am J Sociol 108(1):102–128
Töpfer M (2017) Detailed RIF decomposition with selection: the gender pay gap in Italy (No. 26-2017). Hohenheim Discussion Papers in Business, Economics and Social Sciences
Walby S, Olsen W (2002) The impact of women’s position in the labour market on pay and implications for UK productivity. Women and Equality Unit, London
Weichselbaumer D, Winter-Ebmer R (2005) A meta-analysis of the international gender wage gap. J Econ Surv 19(3):479–511
Acknowledgement
The authors would like to thank the anonymous referees for helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Klaus F. Zimmermann
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix. Oaxaca RIF decomposition of the gender pay gap
Appendix. Oaxaca RIF decomposition of the gender pay gap
Basic model | Reweighted model | |||||
|---|---|---|---|---|---|---|
Q10 | Q50 | Q90 | Q10 | Q50 | Q90 | |
(A) Sample: October 2011 to March 2012 | ||||||
Crude difference | 0.0746 (0.0048373) | 0.2250 (0.0056578) | 0.2379 (0.0077645) | 0.0747 (0.0064611) | 0.2250 (0.0065456) | 0.2379 (0.0101065) |
Explained | 0.0862 (0.0049126) | 0.0744 (0.0051146) | − 0.0067 (0.0058823) | 0.0854 (0.0038475) | 0.0487 (0.0033514) | − 0.0161 (0.0029697) |
Unexplained | − 0.0116 (0.0065747) | 0.1506 (0.0059864) | 0.2446 (0.0089503) | − 0.0107 (0.0063301) | 0.1763 (0.006449) | 0.2540 (0.0104443) |
(B) Sample: October 2017 to March 2018 | ||||||
Crude difference | 0.1431 (0.0050697) | 0.1974 (0.0058705) | 0.2099 (0.0077877) | 0.1420 (0.00814) | 0.1974 (0.0059759) | 0.2100 (0.0093151) |
Explained | 0.0832 (0.0044984) | 0.0533 (0.0052463) | − 0.0162 (0.0052086) | 0.0586 (0.0028377) | 0.0265 (0.0030371) | − 0.0282 (0.0030015) |
Unexplained | 0.0599 (0.0067001) | 0.1441 (0.0062027) | 0.2262 (0.0087298) | 0.0834 (0.0085037) | 0.1709 (0.0059672) | 0.2382 (0.0094618) |
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Meara, K., Pastore, F. & Webster, A. The gender pay gap in the USA: a matching study. J Popul Econ 33, 271–305 (2020). https://doi.org/10.1007/s00148-019-00743-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00148-019-00743-8