Abstract
This paper presents development of a household Nash-bargaining model in an overlapping generation setting to analyze the intergenerational dynamics of education decisions and to analyze cooperatively bargained fertility within a family. A stronger preference by women for the welfare of children induces redistribution from women to men in exchange for higher educational investment in children, although the cost to women of child rearing is compensated by men when women care for their children. Subsequently, this paper presents description of the policy effects on the dynamics that arise from expansion of formal child-care coverage. The policy substitutes time costs that were previously borne by mothers, i.e., a policy targeted at mothers. If the education level of mothers is sufficiently high (low), then the policy lowers (raises) fertility and increases (decreases) investment in education for children in the long term. Most notable is the intermediate case: When a mother’s education level is not too high and not too low, the policy raises both the fertility rate and educational investment in daughters, while probably decreasing investment in sons. The quantity–quality tradeoff for children might not hold. The policy also raises the probability of marriage and the probability of having children.


Similar content being viewed by others
Notes
It is widely perceived that unitary models are not supported empirically (Lundberg et al. 1997; Duflo 2003; Blundell et al. 2007). There are two strands in the literature of family economics: Manser and Brown (1980) and McElroy and Horney (1981) present Nash bargaining models, whereas Chiappori (1988, 1992), Apps and Rees (1997), Komura (2013), and Kemnitz and Thum (2015) present collective approaches. Basu (2006) explains the difference between a collective approach and Nash bargaining.
See, for example, OECD Statistics (Social Expenditure, Public expenditure on family by type of expenditure, in % GDP, http://stats.oecd.org/. Accessed 10 June 2015). Another example is the limited accessibility to formal child care. For example, in Japan, the ratio of the number of children on a waiting list to use day nurseries (“Taiki-Jido” in Japanese) to the total number of children aged 0 to 4 was high, i.e., about 0.81%, in 2014 (Source: Ministry of Health, Labor and Welfare: http://www.mhlw.go.jp/stf/houdou/0000078441.html and National institute of Population and Social Security Research: http://www.ipss.go.jp/shoshika/tokei/Populr/P_Detail2016.asp?fname=T02-02.htm. Both accessed 15 June 2016).
Lundberg and Pollak (1993) proposed the plausibility of separate spheres bargaining.
Echevarria and Merlo (1999) do not discuss policy effects.
Although the feature of the model is counterfactual, the present analysis is meant to characterize the behavior of a representative couple, as described by Echevarria and Merlo (1999).
However, re-negotiations of family decisions have been studied in intertemporal maximization settings. Rasul (2008) uses the Malaysia Family Life Survey to show that spouses bargain without commitment. Mazzocco (2007) also uses US data to test intra-family commitment. Results show that non-commitment collective models might be appropriate for policy-making. Incomplete contracts models include those of Lundberg and Pollak (1993), Konrad and Lommerud (2000), and Rainer (2008).
A contractual solution for marriage market externality would require written contracts involving all families who might be linked through marriage at any future date, which cannot be done in the absence of perfect foresight of future marriages (Doepke and Tertilt 2009).
This assumption might not hold in reality, although it is usually made in the literature (e.g., Iyigun and Walsh 2007a).
The personal ideal numbers of children for women and men older than 15 are reported for OECD countries in Europe and some other countries by OECD Family Database (http://www.oecd.org/social/family/database.htm. Accessed 12 Jan 2017). They are not necessarily perfectly correlated. The database also shows that the OECD average ideal numbers of children are 2.22 for men and 2.28 for women. After surveying the literature related to developing countries, Mason and Taj (1987) conclude that gender differences in fertility goals tend to be smaller in modern, gender-equal conditions. Recently, Doepke and Kindermann (2016) report that a woman’s intention is the more important for having children, although her partner’s agreement greatly increases the probability of having a child.
More general specification makes it impossible to solve the solution analytically.
Psacharopoulos and Patrinos (2004) present a survey of the mean return rates of investment in education for women and men. For the secondary education level, the returns to women are higher, although the mean return to men is slightly higher on the overall education level.
The price of educational investment is taken to be pegged to the goods price, which is assumed to be unity without loss of generality.
We assume the existence of a symmetric equilibrium. Although the first-order conditions are not described in their general format, we make use of the symmetry nature of the equilibrium in deriving these conditions.
The causal relation between parents’ education levels and those of children cannot be readily derived. Black et al. (2005) conclude that high correlations are primarily attributable to family characteristics and inherited ability and not education spillovers. Currie and Moretti (2003) demonstrate that increases in maternal education over the past 30 years have had strong positive effects on birth outcomes such as birth weights. The benefits were estimated to include a reduction of $5.5 to $6 billion in health, education, and other costs. Sewell and Shah (1968) assert that when parents have discrepant levels of educational achievement, which parent’s education has greater effects on educational aspiration and achievement of children depends on the child’s gender and intelligence level and on each parent’s level of educational achievement.
Although Doepke and Tertilt (2009) assume human capital stock formation from generation to generation with intergenerationally external effects, we assume away the intergenerational externalities of human capital.
Nash (1953) showed that, for a unique feasible outcome to be selected, a bargaining solution should have the following four properties: (i) Pareto-optimality, (ii) symmetry, (iii) independence of equivalent utility representation, and (iv) independence of irrelevant alternatives (see Zhang 2005). Proof of the existence and uniqueness of the time path of the present problem (e ft , e mt , n t ) is given in Appendix 1. Stability is examined in Appendix 2.
One can assume a wage tax instead of lump-sum taxes, but the wage tax reduces the opportunity cost of child-rearing at home, thereby exerting positive effects on fertility.
This assumption is not necessary. Although a female worker can care for more than one child. Female workers must be trained specifically to care for children covered by the policy expansion. We assume that such costs are financed entirely by taxes. In reality, although all workers in the (public) child-care service sector might not necessarily be women, the ratio of men is fairly low even in developed countries. For example, see the Japan Gender Equality Bureau Cabinet Office (http//www.gender.go.jp/about_danjo/whitepaper/h26/zentai/html/column/clm_04.html. Accessed 1 January 2015) and the Japanese Embassy in Norway (http://www.no.emb-japan.go.jp/Japanese/Nikokukan/nikokukan_files/danjyobyoudou.pdf. Accessed 1 January 2015).
Otherwise, no individuals get married. For analytical purposes, it is necessary to have at least one married couple.
This wage function means that the wage rate of an individual is zero if his parents did not invest in him. We can instead assume that w(e) = θ ln(a + e) where a > 1, in which case the wage rate is positive even if his parents did not invest in him.
This assumption implies that an increase in the number of children of a generation will not, ceteris paribus, raise that of the next generation by less than the original increase, i.e., ∂n t + 1/∂n t < 1. It is noteworthy that the violation of the inequality does not render the results in the present paper invalid per se. The utility weight on the number of children, which can be equal to or greater than the utility weight on the welfare of offspring, is commonly used in the literature (e.g., de la Croix and Doepke 2003).
The steady state can be unstable if the second inequality is not satisfied. However, under the assumption of perfect foresight, the system is expected to jump to the steady state if it is unstable.
Condition (23) is equivalent to condition |T(J)| < 1 in Appendix 2.
The positive number of children derives from the specification of the utility function. Under a general form of utility function, individuals might have no child, as shown by Hirazawa et al. (2014).
Based on a “natural experiment,” Lundberg et al. (1997) report strong evidence that a substantial shift toward greater expenditures on women’s goods and children’s goods followed the transfer of a substantial child allowance to wives of the UK in the late 1970s. Attanasio and Lechene (2002) also used PROGRESA data of rural Mexico to find that a higher share of income for wives is associated, on average, with significantly higher budget shares of expenditures on clothing for children of both genders.
The transition is assessed in a numerical example presented in the next sub-section.
Controlling the percentages of female occupations and so on, O’Neill (2003) reports that the adjusted female–male wage ratio for ages 35–43 is 97.5% from the 2000 National Longitudinal Survey of Youth data, although the actual ratio was 82.5% in the US in 2014 (OECD Stat http://stats.oecd.org/index.aspx?queryid=54751#).
Even if women and men have the same preferences for children and the same wage functions, i.e., if γ f = γ m, ε f = ε m, and w f(e) = w m(e), we can obtain fundamentally equivalent results related to the policy effects. The assumption that mothers care for their children at home plays an important role in determining the long-term effects of a policy which targets mothers.
Doepke and Kindermann (2016) used the Generations and Gender Programme (GGP) data to show that policies which lower the child-care burden burden for mothers by providing public child care can be more than twice as effective as policies that provide general subsidies for childbearing. However, they do not consider some aspects of educational investment, such as the tradeoff between quantity and quality of children.
For derivation of (33), see Appendix 3.
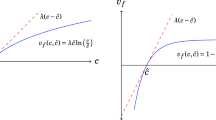
We assume here that the new steady state is sufficiently close to the initial one. The decrease in σ shifts line L to the upper-right in Fig. 1. The fertility rate and educational investment jump to a point on the shifted line.
Different from the analyses explained herein, Iyigun and Walsh (2007b) assert that asymmetries in the sex ratio in the marriage market can generate the difference in premarital investment between sexes in explanation of a rapid increase in the education of women in the USA.
Therefore, the “unmarried threat” is not credible in this case.
References
Alesina A, Giuliano P (2006) Divorce, fertility and the shot gun marriage. IZA Discussion paper No. 2157, Institute for the Study of Labor
Apps PF, Rees R (1997) Collective labor supply and household production. J Political Econ 105(1):178–190
Apps PF, Rees R (2004) Fertility, taxation and family policy. Scand J Econ 106(4):745–763
Attanasio O, Lechene V (2002) Tests of income pooling in household decisions. Rev Econ Dyn 5(4):720–748
Barro RJ, Becker GS (1989) Fertility choice in a model of economic growth. Econometrica 57(2):481–501
Basu K (2006) Gender and say: a model of household behavior with endogenously determined balance of power. Econ J 116(511):558–580
Becker GS, Barro RJ (1988) A reformulation of the economic theory of fertility. Quart J Econ 103(1):1–25
Becker GS, Lewis HG (1973) On the interaction between the quantity and quality of children. J Political Econ 81(2):S279–S288
Black SE, Devereux PJ, Salvanes KG (2005) Why the apple does not fall far: understanding the intergenerational transmission of human capital. Am Econ Rev 95(1):437–449
Blau D, Robins P (1988) Child care costs and family labor supply. Rev Econ Stat 70(3):374–381
Blundell R, Chiappori P-A, Magnac T, Meghir C (2007) Collective labor supply: heterogeneity and non-participation. Rev Econ Stud 74(2):417–445
Case A, Deaton A (1998) Large cash transfers to the elderly in South Africa. Econ J 108(450):1330–1361
Chiappori P-A (1988) Rational household labor supply. Econometrica 56(1):63–89
Chiappori P-A (1992) Collective labor supply and welfare. J Political Econ 100(3):437–467
Currie J, Moretti E (2003) Mother’s education and the intergenerational transmission of human capital: evidence from college openings. Quart J Econ 118(4):1495–1532
Day C (2012) Economic growth, gender wage gap and fertility rebound. Econ Rec 88(6):88–99
Day C (2016) Fertility and economic growth: the role of workforce skill composition and child care price. Oxf Econ Pap 68(2):546–565
De la Croix D, Doepke M (2003) Inequality and growth: why differential fertility matters. Am Econ Rev 93(4):1091–1113
De la Croix D, Donckt MV (2010) Would empowering women initiate the demographic transition in least developed countries? J Hum Cap 4(2):85–129
Doepke M, Kindermann F (2016) Bargaining over babies: theory, evidence, and policy implications. NBER Working Paper 22072, National Bureau of Economic Research
Doepke M, Tertilt M (2009) Women’s liberation: what’s in it for men? Quart J Econ 124(4):1541–1591
Duflo E (2003) Grandmothers and granddaughter: old-age pensions and intrahousehold allocation in South Africa. World Bank Econ Rev 17(1):1–25
Echevarria C, Merlo A (1999) Gender differences in education in a dynamic household bargaining model. Int Econ Rev 40(2):265–286
Feyrer J, Sacerdote B, Stern AD (2008) Will the stork return to Europe and Japan? Understanding fertility within developed nations. J Econ Perspect 22(3):3–22
Goldin C, Katz LF, Kuziemko I (2006) The home-coming of American college women: a reversal of the college gender gap. J Econ Perspect 20(4): 133–156
Hayashi F (1995) Is the Japanese extended family altruistically linked? A test based on Engel Curves. J Political Econ 103(3):661–674
Hazan M, Zoabi H (2015) Do highly educated women choose smaller families? Econ J 125(587):1191–1226
Heckman JJ (1974) Effects of child-care programs on women’s work effort. J Political Econ 82(2):S136–S163
Hirazawa M, Kitaura K, Yakita A (2014) Fertility, intra-generational redistribution, and social security. Can J Econ 47(1):98–114
Iyigun M, Walsh RP (2007a) Endogenous gender power, household labor supply and the demographic transition. J Dev Econ 82(2):138–155
Iyigun M, Walsh RP (2007b) Building the family nest: premarital investments, marriage markets, and spousal allocations. Rev Econ Stud 74(2):507–535
Janta B (2014) Caring for children in Europe: how childcare, parental leave and flexible working arrangements interact in Europe. RAND Europe. http://www.rand.org/content/dam/rand/pubs/research_reports/RR500/RR554/RAND_RR554.pdf. Accessed 26 May 2016
Kemnitz A, Thum M (2015) Gender power, fertility, and family policy. Scand J Econ 117(1):220–247
Komura M (2013) Fertility and endogenous gender bargaining power. J Popul Econ 26(3):943–961
Konrad KA, Lommerud KE (2000) The bargaining family revisited. Can J Econ 33(2):471–487
Luci-Greulich A, Thévenon O (2013) The impact of fertility policies on fertility trends in developed countries. Eur J Popul 29(4):387–416
Luci-Greulich A, Thévenon O (2014) Does economic advancement ‘cause’ a re-increase in fertility? An empirical analysis for OECD countries (1969–2007). Eur J Popul 30(2):187–221
Lundberg S, Pollak RA (1993) Separate spheres bargaining and the marriage market. J Political Econ 101(6):988–1010
Lundberg S, Pollak RA, Wales TJ (1997) Do husbands and wives pool their resources? Evidence from the United Kingdom child benefit. J Hum Resour 32(3):463–480
Manser M, Brown M (1980) Marriage and household decision-making: a bargaining analysis. Int Econ Rev 21(1):31–44
Mason KO, Taj AM (1987) Differences between women’s and men’s reproductive goals in developing countries. Popul Dev Rev 13(4):611–638
Mazzocco M (2007) Household intertemporal behavior: a collective characterization and a test of commitment. Rev Econ Stud 74(3):857–895
McElroy MB, Horney MJ (1981) Nash-bargained household decisions: toward a generalization of the theory of demand. Int Econ Rev 22(2):333–349
Miller G (2008) Women’s suffrage, political responsiveness, and child survival in American history. Quart. J Econ 123(3):1287–1327
Myrskylä M, Kohler H-P, Bolliari FC (2009) Advances in development reverse fertility declines. Nature 460:741–743
Nash J (1953) Two-person cooperative games. Econometrica 21(1):128–140
Olivetti C, Petrongolo B (2017) The economic consequences of family policies: lessons from a century of legislation in high-income countries. J Econ Perspect 31(1):205–230
O’Neill J (2003) The gender gap in wages, circa 200. Am Econ Rev 93(2):309–314
Organisation for Economic Co-operation and Development (OECD) (2012) Education Indicators in Focus: how are girls doing in school—and women doing in employment—around the world? Doi: https://doi.org/10.1787/5k9csf9bxzs7-en. (Accessed 23 June 2016)
Pitt M, Khandker S (1998) The impact of group-based programs on poor households in Bangladesh: does the gender of participants matter? J Political Econ 106(5):958–996
Pollak RA (2011) Family bargaining and taxes: a prolegomenon to the analysis of joint taxation. CESifo Econ Stud 57(2):216–244
Psacharopoulos G, Patrinos HA (2004) Returns to investment in education: a further update. Educ Econ 12(2):111–134
Rainer H (2008) Gender discrimination and efficiency in marriage: the bargaining family under scrutiny. J Popul Econ 21(2):305–329
Rasul I (2008) Household bargaining over fertility: theory and evidence from Malaysia. J Dev Econ 86(2):215–241
Sewell WH, Shah VP (1968) Parents’ education and children’s educational aspirations and achievements. Am Sociol Rev 33(2):191–209
Voena A (2015) Yours, mine, and ours: do divorce laws affect the intertemporal behavior of married couples? Am Econ Rev 105(8):2295–2332
Zhang D (2005) A logical model of Nash bargaining solution. IJCAI 2005. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.122.3236&rep=rep1&type=pdf. Accessed 15 June 2016
Acknowledgements
The author thanks two anonymous referees and the editor of this journal for their insightful comments and helpful suggestions. He is also greatly indebted to Ryo Ishida, Jun-ichi Itaya, Mizuki Komura, Kazutoshi Miyazawa, and seminar participants at The Center for Risk Research of Shiga University, the 2016 Fall Meeting of the Japan Association for Applied Economics, Hokkaido University, Nanzan University, and the Nagoya Macroeconomics Workshop for their comments.
Funding
This work was partially funded by the Japan Society for the Promotion of Science KAKENHI Grant (No. 16H03635).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflict of interest.
Additional information
Responsible editor: Alessandro Cigno
Appendices
Appendix 1 Existence and uniqueness of a family optimum
From (12) and (13), we can obtain e it + 1 as a function of n t , because w i(e it + 1) is monotonic, as
where
Using (34), one can rewrite (14) as
The left-hand side of (37) is decreasing in n t , although the right-hand side is also decreasing in n t . Because the left-hand side is the marginal benefit of an additional child and the left-hand side is the marginal cost, a sufficient condition for the uniqueness of the optimal number of children is
for a given e ft . This condition might be satisfied when the degree of concavity of u(n) or w(e) is sufficiently weak.
When condition (38) holds for relevant ranges of variables, the optimum can exist. From the assumptions for functions u(n) and w(e), the left-hand side of (37) approaches zero as n goes to infinity, although the right-hand side approaches σzw f > 0. Therefore, as long as (37) holds, both sides cross at one point n.
Appendix 2 Uniqueness and stability of steady states
The steady-state values of the number of children and educational investment in daughters, n and e f , are given respectively by the following equations.
To examine local uniqueness and stability of the steady state, linearizing the dynamic system (21) and (22) around the steady state, we obtain the Jacobian matrix as
Denoting the determinant and the trace of matrix J(n, e f ) by D(J) and T(J), we obtain
We have three cases: (i) if both |1 + D(J)| > |T(J)| and |D(J)| < 1 hold, then both eigenvalues are inside the unit interval. Furthermore, the two associated manifolds are stable around the steady state. (ii) If |1 + D(J)| > |T(J)| and |D(J)| > 1 hold, then both eigenvalues are outside of the unit interval, and the associated manifolds are unstable around the steady state. (iii) If |1 + D(J)| < |T(J)|, then one eigenvalue is inside of the unit interval. The other is outside of the unit interval. One stable and one unstable manifold exist around the steady state. The steady state is (saddle-point) unstable in this case.
In this dynamic system of (21) and (22), because we have |D(J)| = 0 and 1 > T(J) under the assumption that 2(ε m + ε f) − (θ m + θ f)(γ m + γ f) < 0, only case (i) is possible.
Next, from (21) and (22), one obtains
The fertility rate and mother’s education level in each period must satisfy condition (39), which is presented as a dotted line L in Fig. 1. Letting (n ∗, e f ∗) be the stable steady state, the dynamics can be shown by arrows in Fig. 1. Assuming that the initial condition is given as \( \left({n}_{t_0-1},{e}_{ft_0}\right) \) in period t 0 and that the initial point is not on line L, the fertility rate in period t 0 jumps to a point corresponding to \( {e}_{ft_0} \) on line L; then the system converges to the steady state S along the line. The steady state is unique and stable if it exists.
Appendix 3 Condition for marriage
In the steady state, we have
where we use (16) and (17). From (45) and (46), we obtain
For men to marry, both conditions V f(e f , em f ) > w f(e f ) − T/2 must hold, where T = (1 − σ)znw f(e f ). From (47), it follows that
where
The left-hand side of (49) is the utility derived from having children. The right-hand side represents the cost of rearing children. Similarly, using (48), it can be shown that condition V m(e m , e f ) > w m(e m ) − T/2 for women is also reduced to (49).
Rights and permissions
About this article
Cite this article
Yakita, A. Fertility and education decisions and child-care policy effects in a Nash-bargaining family model. J Popul Econ 31, 1177–1201 (2018). https://doi.org/10.1007/s00148-017-0675-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00148-017-0675-7