Endogenous fertility in a growth model with public and private health expenditures

Abstract

We build an overlapping-generations model that incorporates endogenous fertility choices, in addition to public and private expenditures on health. Following the seminal analysis of Bhattacharya and Qiao (J Econ Dyn Control 31:2519–2535, 2007) we assume that the effect of public health investment is complementary to private health expenditures. We find that this effect reinforces the positive impact of the capital stock on aggregate saving. Furthermore, we show that this complementarity can provide an additional explanation behind a salient feature of demographic transition; that is, the fertility decline along the process of economic growth.

Appendix

1.1 Proof to Proposition 1

Using Eq. 18, we can define

$$ J\left( {qn_t ,k_t } \right)=qn_t -\frac{\gamma }{1+\beta \left[ {1+\delta Z\left( {\tau \left( {1-\alpha } \right)Ak_t^\alpha \left( {1-qn_t } \right)^{1-\alpha }} \right)} \right]+\gamma }. $$

(36)

We can also use Eqs. 6, 10 and 15 to write

$$ \tau \left( {1-\alpha } \right)Ak_t^\alpha \left( {1-qn_t } \right)^{1-\alpha }=p_{t+1} . $$

(37)

From Eq. 36 we have

$$ J_{k_t}{\kern1pt} ({\cdot ,\cdot}) {\kern-1pt}={\kern-1pt}\frac{\gamma \beta \delta {Z}' {\kern-1pt}\left( {\tau {\kern-1pt}\left( {1{\kern-1pt}-{\kern-1pt}\alpha } \right){\kern-1pt} Ak_t^\alpha {\kern-1pt}\left( {1-qn_t } \right)^{1-\alpha }} \right){\kern-1pt}\tau{\kern-1pt}\left( {1{\kern-1pt}-{\kern-1pt}\alpha } \right)A\alpha k_t^{\alpha -1} \left( {1{\kern-1pt}-{\kern-1pt}qn_t } \right)^{1-\alpha }}{\left\{ {1{\kern-1pt}+{\kern-1pt}\beta \left[ {1{\kern-1pt}+{\kern-1pt}\delta Z\left( {\tau \left( {1{\kern-1pt}-{\kern-1pt}\alpha } \right)Ak_t^\alpha \left( {1{\kern-1pt}-{\kern-1pt}qn_t } \right)^{1-\alpha }} \right)} \right]{\kern-1pt}+{\kern-1pt}\gamma } \right\}^2}>0. $$

(38)

Alternatively, we can substitute Eq. 37 in Eq. 38 to write

$$ J_{k_t } \left( {\cdot ,\cdot } \right)=\frac{\gamma \beta \delta \alpha {Z}'\left( {p_{t+1} } \right)p_{t+1} }{\left\{ {1+\beta \left[ {1+\delta Z\left( {p_{t+1} } \right)} \right]+\gamma } \right\}^2k_t }>0. $$

(39)

From Eq. 36, we can also derive

$$ J_{qn_t } \left( {\cdot ,\cdot } \right)=1-\frac{\gamma \beta \delta {Z}'\left( {\tau \left( {1-\alpha } \right)Ak_t^\alpha \left( {1-qn_t } \right)^{1-\alpha }} \right)\tau \left( {1-\alpha } \right)^2Ak_t^\alpha \left( {1-qn_t } \right)^{-\alpha }}{\left\{ {1+\beta \left[ {1+\delta Z\left( {\tau \left( {1-\alpha } \right)Ak_t^\alpha \left( {1-qn_t } \right)^{1-\alpha }} \right)} \right]+\gamma } \right\}^2}, $$

(40)

to which we can substitute Eq. 37 to get

$$ J_{qn_t } \left( {\cdot ,\cdot } \right)=1-\frac{\gamma \beta \delta \left( {1-\alpha } \right){Z}'\left( {p_{t+1} } \right)p_{t+1} }{\left\{ {1+\beta \left[ {1+\delta Z\left( {p_{t+1} } \right)} \right]+\gamma } \right\}^2\left( {1-qn_t } \right)}. $$

(41)

Substituting Eqs. 18 and 37 in Eq. 41, we can write the latter as

$$ J_{qn_t } \left( {\cdot ,\cdot } \right)=1-\frac{\gamma }{1+\beta \left[ {1+\delta Z\left( {p_{t+1} } \right)} \right]+\gamma }\frac{\left( {1-\alpha } \right)\beta \delta {Z}'\left( {p_{t+1} } \right)p_{t+1} }{1+\beta \left[ {1+\delta Z\left( {p_{t+1} } \right)} \right]}>0, $$

(42)

which is positive because ${Z}^{\prime}\left( {p_{t+1} } \right)p_{t+1} <Z\left( {p_{t+1} } \right)$ holds. Now, we can combine the results in Eqs. 42 and 38, and apply the implicit function theorem to Eq. 36. This yields

$$ \frac{dqn_t }{dk_t }=-\frac{J_{k_t } \left( {\cdot ,\cdot } \right)}{J_{qn_t } \left( {\cdot ,\cdot } \right)}<0, $$

(43)

Therefore, given that q is a fixed parameter, we can conclude that $n_t =n\left( {k_t } \right)$ such that ${n}'\left( {k_t } \right)<0$. Finally, we can use the previous analysis to write Eq. 17 as

$$ \begin{array}{rll} s_t &=& \frac{\beta \big[ {1+\delta Z\big( {\tau \left( {1-\alpha } \right)Ak_t^\alpha \left( {1-qn\left( {k_t } \right)} \right)^{1-\alpha }} \big)} \big]}{1+\beta \big[ {1+\delta Z\big ( {\tau \left( {1-\alpha } \right)Ak_t^\alpha \left( {1-qn\left( {k_t } \right)} \right)^{1-\alpha }} \big)} \big]}\left( {1-\tau } \right)\left( {1-\alpha } \right) \\ && \times Ak_t^\alpha \left( {1-qn\left( {k_t } \right)} \right)^{1-\alpha }, \end{array} $$

from which it is straightforward to establish that ds _t /dk _t  > 0. □

1.2 Proof to Proposition 2

From Eqs. 18 and 20, we can establish that $n\left( 0 \right)=\frac{\gamma /q}{1+\beta \left( {1+\delta } \right)+\gamma }$ and $n\left( \infty \right)=\frac{\gamma /q}{1+\beta \left( {1+\delta \bar{{\varepsilon }}} \right)+\gamma }$. Combining these with Eq. 22, we see that $\psi \left( 0 \right)=0$ and $\psi \left( \infty \right)=\infty$. Furthermore, it is

$$ \begin{array}{rll} {\psi }'(k_t ) &=& \eta \left\langle {\frac{\beta \big[ {1+\delta Z\big( {\tau \left( {1-\alpha } \right)Ak_t^\alpha \left( {1-qn\left( {k_t } \right)} \right)^{1-\alpha }} \big)} \big]}{1+\beta \big[{1+\delta Z\big( {\tau \left( {1-\alpha } \right)Ak_t^\alpha \left( {1-qn\left( {k_t } \right)} \right)^{1-\alpha }} \big)} \big]}} \right. \\ &&{\kern13.5pt} \times \frac{\theta \left( {k_t } \right)}{n\left( {k_t } \right)} +\, \frac{k_t^\alpha \left( {1-qn\left( {k_t } \right)} \right)^{1-\alpha }}{n\left( {k_t } \right)} \\ &&{\kern13.5pt} \times \frac{\beta \delta {Z}'\big( {\tau \left( {1-\alpha } \right)Ak_t^\alpha \left( {1-qn\left( {k_t } \right)} \right)^{1-\alpha }} \big)\tau \left( {1-\alpha } \right)A\theta \left( {k_t } \right)}{\big\{1+\beta \big[1+\delta Z\big( {\tau (1-\alpha )Ak_t^\alpha \left( {1-qn\left( {k_t } \right)} \right)^{1-\alpha }} \big)\big]\big\}^2} \\ &&{\kern13.5pt} - \left. \frac{\beta \big[1+\delta Z\left( {\tau (1-\alpha )Ak_t^\alpha (1-qn(k_t ))^{1-\alpha }} \right)\big]}{1+\beta \big[1+\delta Z\left( {\tau (1-\alpha )Ak_t^\alpha (1-qn(k_t ))^{1-\alpha }} \right)\big]} \right. \\ &&{\kern13.5pt} \left. \times \frac{k_t^\alpha (1-qn(k_t ))^{1-\alpha }}{[n(k_t )]^2}{n}'(k_t ) \vphantom{{\frac{\beta \big[ {1+\delta Z\big( {\tau \left( {1-\alpha } \right)Ak_t^\alpha \left( {1-qn\left( {k_t } \right)} \right)^{1-\alpha }} \big)} \big]}{1+\beta \big[{1+\delta Z\big( {\tau \left( {1-\alpha } \right)Ak_t^\alpha \left( {1-qn\left( {k_t } \right)} \right)^{1-\alpha }} \big)} \big]}}}\right\rangle , \end{array} $$

(44)

where

$$\theta (k_t )=\alpha k_t^{\alpha -1} (1-qn(k_t ))^{1-\alpha }-k_t^\alpha (1-\alpha )q{n}'(k_t )(1-qn(k_t ))^{-\alpha }. $$

(45)

Clearly, ψ′(k _t ) > 0. Now, combine Eqs. 39 and 42 to write Eq. 43 as

$$ \begin{array}{rll} \frac{dqn_t }{dk_t } &{\kern-1pt}={\kern-1pt}& -\frac{\gamma \beta \delta \alpha {Z}'\left( {p_{t+1} } \right)p_{t+1} \{1+\beta [1+\delta Z\left( {p_{t+1} } \right)]\}}{\{1{\kern-1pt}+{\kern-1pt}\beta [1{\kern-1pt}+{\kern-1pt}\delta Z\left( {p_{t+1} } \right)]{\kern-1pt}+{\kern-1pt}\gamma \}\{1{\kern-1pt}+{\kern-1pt}\beta [1{\kern-1pt}+{\kern-1pt}\delta Z\left( {p_{t+1} } \right)]\}{\kern-1pt}-{\kern-1pt}\gamma \beta \delta (1{\kern-1pt}-{\kern-1pt}\alpha ){Z}'\left( {p_{t+1} } \right)p_{t+1} } \\ && \times \frac{1}{k_t \{1+\beta [1+\delta Z\left( {p_{t+1} } \right)]+\gamma \}}. \\ \end{array} $$

Given Z′(0) = ϕ and Z′( ∞ ) = 0, we can combine the expression above together with Eq. 37, $n(0)=\frac{\gamma /q}{1+\beta (1+\delta )+\gamma }$ and $n(\infty )=\frac{\gamma /q}{1+\beta (1+\delta \bar{{\varepsilon }})+\gamma }$ to establish that

$$ {n}'\left( {k_t } \right)=\left\{ {{\begin{array}{*{20}c} {-\infty } & {\mbox{for}} & {k_t =0} \\ 0 & {\mbox{for}} & {k_t \to \infty } \\ \end{array} }} \right.. $$

(46)

Combining Eqs. 45 and 46 with Eq. 44, we infer that

$$ {\psi }'\left( {k_t } \right)=\left\{ {{\begin{array}{*{20}c} \infty & {\mbox{for}} & {k_t =0} \\ 0 & {\mbox{for}} & {k_t \to \infty } \\ \end{array} }.} \right. $$

(47)

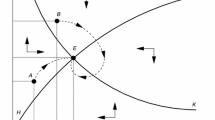
Thus, we conclude that there must be at least one $\hat{{k}}\in \left( {0,\infty } \right)$ such that $\hat{{k}}=\psi (\hat{{k}})$ and ${\psi}^{\prime}(\hat{{k}})<1$, i.e. $\hat{{k}}$ is a stable steady-state equilibrium. □