Abstract
Introduced by Samuelson (Int Econ Rev 16(3):531–538, 1975), the Serendipity Theorem states that the competitive economy will converge towards the optimum steady-state provided the optimum fertility rate is imposed. This paper aims at exploring whether the Serendipity Theorem still holds in an economy with risky lifetime. We show that, under general conditions, including a perfect annuity market with actuarially fair return, imposing the optimum fertility rate and the optimum survival rate leads the competitive economy to the optimum steady state. That Extended Serendipity Theorem is also shown to hold in economies where old adults work some fraction of the old age, whatever the retirement age is fixed or chosen by the agents.
Similar content being viewed by others
Notes
That assumption is clearly strong. We shall discuss that issue in more details below.
In other words, imposing the optimum fertility makes the competitive economy converge toward the most golden rule steady state, provided this one exists, is unique and stable. Otherwise, the convergence would not occur, and the social optimum could not be decentralized by means of the fertility rate.
Note that taking demographic variables as inputs does not necessarily legitimate an intervention by the State. It is the particular approach adopted by Samuelson that treats demographic variables as instruments of the government, allowing for the decentralization of the social optimum, by making the solutions of the optimization problems of the social planner and of the agents coincide (see below).
On the difficulties raised by population ethics, see Blackorby et al. (2005).
That function is used by De la Croix and Michel (2002, p. 4).
In the spirit of Samuelson’s work, we will focus mainly here on conditions characterizing an interior optimum. However, we will discuss the plausibility of a corner optimum survival rate below. Note also that we assume, like Samuelson, that the social optimum is unique, that is, that only one set of variables satisfy the above FOCs. This guarantees that our optimum is necessarily a global optimum.
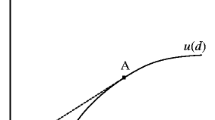
To illustrate the crucial role played by the shape of u(·), the Appendix, Electronic Supplementary Material concentrates on the case of a constant intertemporal elasticity of substitution (CIES) utility function with an intercept.
In that case, the low production capacity, by restraining consumption below a level making a life-period enjoyable, makes a short life better than a long life from the perspective of total lifetime welfare.
Actually, that case seems implausible for advanced economies with large production capacities.
See the Appendix, Electronic Supplementary Material for the derivation.
In the Appendix, Electronic Supplementary Material, we derive the FOCs and SOCs in the special case of a CIES utility function and a Cobb–Douglas production function and discuss the cases under which those conditions are satisfied.
That assumption, which is most common in the literature (see Chakraborty 2004), involves a strong simplification, since annuity markets are largely underdeveloped in the real world (see Brown 2007). Note, however, that the Serendipity Theorem concerns a perfectly competitive economy, so that assuming perfect annuity markets seems to be the most natural assumption for the purpose at hand.
Note that, in the case where the optimum survival rate π ⋆ is zero, this Extended Serendipity Theorem does not hold. Indeed, if the social planner imposes π ⋆ = 0 to individuals, these will not save any more. As a consequence, we have, at the steady state, k = 0, whereas the Serendipity Theorem focuses on steady states with a strictly positive capital level.
Note also that if agents could, at the laissez-faire, affect their survival probability (e.g., through health spending), then there may be a difference between the laissez-faire and the social optimum, as agents may ignore the effect of their health investment on the return of their savings, and choose a non-optimal level of health investment (see Becker and Philipson 1998). This possibility does not arise here, where agents take the demographic parameters n and π as given.
In that alternative framework, life expectancy is equal to 1 + h, against 1 + π in the present setting, but the difference is that survival curves would then be perfectly rectangular (see Jouvet et al. 2010).
Note also that there exists a third way to introduce longevity in a two-period setting: This consists of making agents face a probability π to enjoy a second period of length h, which yields a life expectancy equal to 1 + πh (see Ponthiere 2009). Under that alternative framework, the Extended Serendipity Theorem would still hold provided perfect annuity markets and average utilitarianism are assumed.
Under critical-level utilitarianism, the social objective function is not an average of individual utilities, but a sum of individual utilities net of a critical welfare level (which, by definition, makes a life neutral from the perspective of social welfare).
Actually, mortality, as introduced in Section 3, does not affect the proportion of current savers with respect to future workers, which is a key ratio explaining why the demography matters in the theory of optimal capital accumulation. We explore here what happens when π affects that ratio.
Note that there may exist other ways to introduce old-age labor in the present framework. Here we adopted the most convenient formalization.
That additional negative effect tends to counteract the standard intergenerational transfer effect mentioned in Section 3. Indeed condition 22 can be rewritten as
$$ -k^\star+ \frac{\pi^\star}{(n^\star)^{2}}\left(d^\star-\lambda F_{L}\left( k^\star,1+\frac{\lambda \pi^\star }{n^\star}\right)\right) =0 $$The standard intergenerational transfer effect (i.e., the second term) is here reduced by the fact that old agents do not only consume but also produce (under λ > 0), as shown by the second term in brackets.
See the Appendix, Electronic Supplementary Material for the derivation.
Note, however, that the agent’s objective function is, in our model, additive over time, so that the decision concerning the retirement age is necessarily time consistent.
However, that robustness of the Extended Serendipity Theorem remains conditional on the particular way in which old-age labor is modeled in our framework. The present work has thus no pretension to exhaustiveness and could be complemented by additional robustness studies (see below).
Note that, more generally, additional discussions on the normative foundations of Samuelson’s approach would also be welcome, since one may accuse such an instrumental use of demographic variables of excess normativism. But such discussions on the normative foundations of population economics would require an entire paper on their own and are thus left for future research.
References
Abio G (2003) Interiority of the optimal population growth rate with endogenous fertility. Econ Bull 10(4):1–7
Abio G, Mahieu C, Paxtot C (2004) On the optimality of PAYG pension systems in an endogenous fertility setting. J Pensions Econ Finance 3(1):35–62
Becker G, Philipson T (1998) Old-age longevity and mortality contingent claims. J Polit Econ 106(3):551–573
Blackburn K, Cipriani GP (2002) A model of longevity, fertility and growth. J Econ Dyn Control 26(2):187–204
Blackorby C, Bossert W, Donaldson, D (2005) Population issues in social choice theory, welfare economics and ethics. Econometric Society Monographs. Cambridge University Press, Cambridge
Brown JR (2007) Rational and behavioural perspectives on the role of annuities in retirement planning. NBER working paper 13537
Cervellati M, Sunde U (2007) Fertility, education, and mortality: a unified theory of the economic and demographic transition. Mimeo, IZA, Bonn
Chakraborty S (2004) Endogenous lifetime and economic growth. J Econ Theory 116:119–137
Deardorff AV (1976) The optimum growth rate for population: comment. Int Econ Rev 17(2):510–515
De la Croix D, Mahieu, G Rillaers A (2004) How should the allocation of resources adjust to the baby bust? J Public Econ Theory 6(4):607–636
De la Croix D, Michel P (2002) A theory of economic growth. Dynamics and policy in overlapping generations. Cambridge University Press, Cambridge
De la Croix D, Licandro O (2007) The child is the father of man—implications for the demographic transition. CORE discussion paper 2007-72
De la Croix D, Ponthiere G (2010) On the Golden Rule of capital accumulation under endogenous longevity. Math Soc Sci 59(2):227–238
Diamond P (1965) National debt in a neoclassical growth model. Am Econ Rev 55(5):1126–1150
Doepke M (2004) Accounting for fertility decline during the transition to growth. J Econ Growth 9(3):347–383
Galor O, Moav O (2005) Natural selection and the evolution of life expectancy, CEPR. Minerva Center for Economic Growth paper 02-05
Hu S (1979) Social security, the supply of labor, and capital accumulation. Am Econ Rev 69(3):274–283
Jaeger K, Kuhle W (2009) The optimum growth rate for population reconsidered. J Popul Econ 22(1):23–41
Jouvet PA, Pestieau P, Ponthiere G (2010) Longevity and environmental quality in an OLG model. J Econ 100(3):191–216
Michel P, Pestieau P (1993) Population growth and optimality: when does the serendipity hold. J Popul Econ 6(4):353–362
Parfit D (1984) Reasons and persons. Oxford University Press, Oxford
Ponthiere G (2009) Rectangularization and the rise of limit-longevity in a simple overlapping generations model. Manchester School 77(1):17–46
Samuelson P (1975) The optimum growth rate for population. Int Econ Rev 16(3):531–538
Acknowledgements
The authors are grateful to Raouf Boucekkine, Hyppolite d’Albis, Julio Davila, Wolfgang Kuhle, Bertrand Wigniolle, and two anonymous referees for their helpful comments on this paper. The first author acknowledges the financial support of the Belgian French speaking community (Grant ARC “Sustainability”) and the Belgian Federal Government (Grant PAI P6/07 Glonomics).
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editor: Junsen Zhang
Electronic Supplementary Material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
de la Croix, D., Pestieau, P. & Ponthière, G. How powerful is demography? The Serendipity Theorem revisited. J Popul Econ 25, 899–922 (2012). https://doi.org/10.1007/s00148-011-0362-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00148-011-0362-z