Abstract
We present a new multiparty protocol for the distributed generation of biprime RSA moduli, with security against any subset of maliciously colluding parties assuming oblivious transfer and the hardness of factoring. Our protocol is highly modular, and its uppermost layer can be viewed as a template that generalizes the structure of prior works and leads to a simpler security proof. We introduce a combined sampling-and-sieving technique that eliminates both the inherent leakage in the approach of Frederiksen et al. (Crypto’18) and the dependence upon additively homomorphic encryption in the approach of Hazay et al. (JCrypt’19). We combine this technique with an efficient, privacy-free check to detect malicious behavior retroactively when a sampled candidate is not a biprime and thereby overcome covert rejection-sampling attacks and achieve both asymptotic and concrete efficiency improvements over the previous state of the art.
Notes
Prior works generally consider RSA key generation and include steps for generating shares of e and d such that \(e\cdot d \equiv 1 \pmod {\varphi (N)}\). This work focuses only on the task of sampling the RSA modulus \(N\). Prior techniques can be applied to sample (e, d) after sampling \(N\), and the distributed generation of an RSA modulus has standalone applications, such as for generating the trusted setup required by verifiable delay functions [41, 50]; consequently, we omit further discussion of e and d.
The folklore technique involves invoking the protocol iteratively, each iteration eliminating one corrupt party until a success occurs. For a constant fraction of corruptions, the implied linear round complexity overhead can be reduced to super-constant (e.g., \(\log ^*{n}\)) [15].
In other words, a biprime of length \(2{\kappa } \) provides \({\lambda } \) bits of security.
Technically, Katz and Lindell specify that sampling failures are permitted with negligible probability, and require \(\mathsf {GenModulus} \) to run in strict polynomial time. We elide this detail.
Boneh and Franklin actually propose two variations, one of which has no false negatives; we choose the other variation, as it leads to a more efficient sampling protocol.
This technique is known in the literature of residue number systems as the Szabo–Tanaka method for RNS base extension [48].
This is accomplished by testing \(\gcd (z \bmod {N},N)=1\), which is equivalent as any factor of z and N also divides \(z\bmod {N}\).
Where \({\lambda } \) is a computational security parameter as described in Sect. 2.
Including the wires required to input the randomness for the GCD test.
Assuming the intermediate products inside each invocation of
 are taken to be of length \(2{\kappa } +|\max ({\varvec{\mathrm {m}}})|\), and that each party’s shares of \(p\) and \(q\) are taken to be \({\kappa }-\log _2n\) bits after their lengths are checked.
are taken to be of length \(2{\kappa } +|\max ({\varvec{\mathrm {m}}})|\), and that each party’s shares of \(p\) and \(q\) are taken to be \({\kappa }-\log _2n\) bits after their lengths are checked.\(O({\kappa } ^{\log _23})\) is the cost of Karatsuba multiplication on \({\kappa } \)-bit inputs.
We do not know the precise probability, nor does any prior work, including that of Boneh and Franklin [5] themselves, make a statement about it. It seems empirically that the probability is very low indeed. For analysis purposes we take it to be zero.
As described in their work, their circuit contains additional gates for calculating parts of the RSA key-pair other than the modulus. We omit these parts from our analysis, for the sake of fairness.
We calculate their circuit size using the building blocks we previously described in Table 3 and use their estimate of 6000 gates for the cost of a single AES call.
Assuming that in their case, the adversary never forces the rejection of valid candidates.
We define a function in order to express other costs in terms of this cost; note that the variables n, \({s} \) and \({\lambda } \) are assumed to be global, and thus for simplicity we do not include them among the function’s parameters.
Note that the constituent multipliers in this case admit cheats, which are caught later by the Cheater Check command, if it is invoked
See the first branch of Step 5 of
 for a detailed algorithm to sample such views.
for a detailed algorithm to sample such views.The emulated honest parties abort upon discovering that the candidate really was a biprime during the privacy-free consistency check.
Note that because the protocol does not permit the adversary to input shares of \(p\) or \(q\) with the wrong residues modulo 4, the abort in the Sampling phase of
 can never be triggered.
can never be triggered.
References
Joy Algesheimer, Jan Camenisch, and Victor Shoup. Efficient computation modulo a shared secret with application to the generation of shared safe-prime products. In Advances in Cryptology – CRYPTO 2002, pages 417–432, 2002.
Elaine Barker. Nist special publication 800-57, part 1, revision 4. https://doi.org/10.6028/NIST.SP.800-57pt1r4, 2016.
Michael Ben-Or and Ran El-Yaniv. Resilient-optimal interactive consistency in constant time. Distributed Computing, 16(4):249–262, 2003.
Dan Boneh and Matthew K. Franklin. Efficient generation of shared RSA keys. In Advances in Cryptology – CRYPTO 1997, pages 425–439, 1997.
Dan Boneh and Matthew K. Franklin. Efficient generation of shared RSA keys. Journal of the ACM, 48(4):702–722, 2001.
Elette Boyle, Geoffroy Couteau, Niv Gilboa, Yuval Ishai, Lisa Kohl, Peter Rindal, and Peter Scholl. Efficient two-round OT extension and silent non-interactive secure computation. In Proceedings of the 26th ACM Conference on Computer and Communications Security, (CCS), pages 291–308, 2019.
Ran Canetti. Universally composable security: A new paradigm for cryptographic protocols. In Proceedings of the 42nd Annual Symposium on Foundations of Computer Science (FOCS), pages 136–145, 2001.
Ran Canetti, Yehuda Lindell, Rafail Ostrovsky, and Amit Sahai. Universally composable two-party and multi-party secure computation. In Proceedings of the 34th Annual ACM Symposium on Theory of Computing (STOC), pages 494–503, 2002.
Megan Chen, Ran Cohen, Jack Doerner, Yashvanth Kondi, Eysa Lee, Schuyler Rosefield, and abhi shelat. Muliparty generation of an RSA modulus. In Advances in Cryptology – CRYPTO 2020, part III, pages 64–93, 2020.
Megan Chen, Carmit Hazay, Yuval Ishai, Yuriy Kashnikov, Daniele Micciancio, Tarik Riviere, abhi shelat, Muthuramakrishnan Venkitasubramaniam, and Ruihan Wang. Diogenes: Lightweight scalable RSA modulus generation with a dishonest majority. http://eprint.iacr.org/2020/374, 2020.
Clifford Cocks. Split knowledge generation of RSA parameters. In Proceedings of the 6th International Conference on Cryptography and Coding, pages 89–95, 1997.
Clifford Cocks. Split generation of RSA parameters with multiple participants. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.177.2600, 1998.
Ran Cohen, Sandro Coretti, Juan Garay, and Vassilis Zikas. Round-preserving parallel composition of probabilistic-termination cryptographic protocols. In Proceedings of the 44th International Colloquium on Automata, Languages, and Programming (ICALP), pages 37:1–37:15, 2017.
Ran Cohen, Sandro Coretti, Juan A. Garay, and Vassilis Zikas. Probabilistic termination and composability of cryptographic protocols. Journal of Cryptology, 32(3):690–741, 2019.
Ran Cohen, Iftach Haitner, Eran Omri, and Lior Rotem. From fairness to full security in multiparty computation. In Proceedings of the 11th Conference on Security and Cryptography for Networks (SCN), pages 216–234, 2018.
Ran Cohen and Yehuda Lindell. Fairness versus guaranteed output delivery in secure multiparty computation. Journal of Cryptology, 30(4):1157–1186, 2017.
Ronald Cramer, Ivan Damgård, and Yuval Ishai. Share conversion, pseudorandom secret-sharing and applications to secure computation. In Proceedings of the Second Theory of Cryptography Conference, TCC 2005, pages 342–362, 2005.
Ivan Damgård and Gert Læssøe Mikkelsen. Efficient, robust and constant-round distributed RSA key generation. In Proceedings of the 7th Theory of Cryptography Conference, TCC 2010, pages 183–200, 2010.
Jack Doerner, Yashvanth Kondi, Eysa Lee, and Abhi Shelat. Secure two-party threshold ECDSA from ECDSA assumptions. In Proceedings of the 39th IEEE Symposium on Security and Privacy, (S&P), pages 980–997, 2018.
Jack Doerner, Yashvanth Kondi, Eysa Lee, and Abhi Shelat. Threshold ECDSA from ECDSA assumptions: The multiparty case. In Proceedings of the 40th IEEE Symposium on Security and Privacy, (S&P), 2019.
Shimon Even, Oded Goldreich, and Abraham Lempel. A randomized protocol for signing contracts. Communications of the ACM, 28(6):637–647, 1985.
Yair Frankel, Philip D. MacKenzie, and Moti Yung. Robust efficient distributed RSA-key generation. In Proceedings of the 17th Annual ACM Symposium on Principles of Distributed Computing (PODC), page 320, 1998.
Tore Kasper Frederiksen, Yehuda Lindell, Valery Osheter, and Benny Pinkas. Fast distributed RSA key generation for semi-honest and malicious adversaries. In Advances in Cryptology – CRYPTO 2018, part II, pages 331–361, 2018.
Niv Gilboa. Two party RSA key generation. In Advances in Cryptology – CRYPTO 1999, pages 116–129, 1999.
Oded Goldreich. The Foundations of Cryptography - Volume 1: Basic Techniques. Cambridge University Press, 2001.
Oded Goldreich, Silvio Micali, and Avi Wigderson. How to play any mental game or A completeness theorem for protocols with honest majority. In Proceedings of the 19th Annual ACM Symposium on Theory of Computing (STOC), pages 218–229, 1987.
Shafi Goldwasser and Yehuda Lindell. Secure multi-party computation without agreement. Journal of Cryptology, 18(3):247–287, 2005.
Carmit Hazay, Gert Læssøe Mikkelsen, Tal Rabin, and Tomas Toft. Efficient RSA key generation and threshold Paillier in the two-party setting. In Topics in Cryptology - CT-RSA 2012 - The Cryptographers’ Track at the RSA Conference, pages 313–331, 2012.
Carmit Hazay, Gert Læssøe Mikkelsen, Tal Rabin, Tomas Toft, and Angelo Agatino Nicolosi. Efficient RSA key generation and threshold paillier in the two-party setting. Journal of Cryptology, 32(2):265–323, 2019.
Carmit Hazay, Peter Scholl, and Eduardo Soria-Vazquez. Low cost constant round MPC combining BMR and oblivious transfer. In Advances in Cryptology – ASIACRYPT 2017, part I, pages 598–628, 2017.
Russell Impagliazzo and Moni Naor. Efficient cryptographic schemes provably as secure as subset sum. Journal of Cryptology, 9(4):199–216, 1996.
Yuval Ishai, Rafail Ostrovsky, and Vassilis Zikas. Secure multi-party computation with identifiable abort. In Advances in Cryptology – CRYPTO 2014, part II, pages 369–386, 2014.
Marc Joye and Richard Pinch. Cheating in split-knowledge RSA parameter generation. In Workshop on Coding and Cryptography, pages 157–163, 1999.
Jonathan Katz and Yehuda Lindell. Introduction to Modern Cryptography, Second Edition, chapter Digital Signature Schemes, pages 443–486. Chapman & Hall/CRC, 2015.
Marcel Keller, Emmanuela Orsini, and Peter Scholl. Actively secure OT extension with optimal overhead. In Advances in Cryptology – CRYPTO 2015, part I, pages 724–741, 2015.
Donald E. Knuth. The Art of Computer Programming, Volume II: Seminumerical Algorithms. Addison-Wesley, 1969.
Michael Malkin, Thomas Wu, and Dan Boneh. Experimenting with shared RSA key generation. In Proceedings of the Internet Society’s 1999 Symposium on Network and Distributed System Security, pages 43–56, 1999.
Gary L. Miller. Riemann’s hypothesis and tests for primality. J. Comput. Syst. Sci., 13(3):300–317, 1976.
Payman Mohassel and Matthew K. Franklin. Efficiency tradeoffs for malicious two-party computation. In Proceedings of the 9th International Conference on the Theory and Practice of Public-Key Cryptography (PKC), pages 458–473, 2006.
Michele Orrù, Emmanuela Orsini, and Peter Scholl. Actively secure 1-out-of-n OT extension with application to private set intersection. In Topics in Cryptology - CT-RSA 2017 - The Cryptographers’ Track at the RSA Conference, pages 381–396, 2017.
Krzysztof Pietrzak. Simple verifiable delay functions. In Proceedings of the 10th Annual Innovations in Theoretical Computer Science (ITCS) conference, pages 60:1–60:15, 2019.
Guillaume Poupard and Jacques Stern. Generation of shared RSA keys by two parties. In Advances in Cryptology – ASIACRYPT 1998, pages 11–24, 1998.
Michael O. Rabin. Probabilistic algorithm for testing primality. Journal of Number Theory, 12(1):128–138, 1980.
Ronald L. Rivest. A description of a single-chip implementation of the RSA cipher, 1980.
Ronald L. Rivest. RSA chips (past/present/future). In Workshop on the Theory and Application of Cryptographic Techniques, pages 159–165. Springer, 1984.
Ronald L. Rivest, Adi Shamir, and Leonard M. Adleman. A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 21(2):120–126, 1978.
J. Barkley Rosser and Lowell Schoenfeld. Approximate formulas for some functions of prime numbers. Illinois J. Math., 6:64–94, 1962.
Richard I. Szabo and Nicholas S. Tanaka. Residue Arithmetic and Its Application to Computer Technology. McGraw-Hill, 1967.
Xiao Wang, Samuel Ranellucci, and John Katz. Global-scale secure multiparty computation. In Proceedings of the 24th ACM Conference on Computer and Communications Security, (CCS), pages 39–56, 2017.
Benjamin Wesolowski. Efficient verifiable delay functions. In Advances in Cryptology – EUROCRYPT 2019, part III, pages 379–407, 2019.
Kang Yang, Xiao Wang, and Jiang Zhang. More efficient MPC from improved triple generation and authenticated garbling. In Proceedings of the 27th ACM Conference on Computer and Communications Security, (CCS), 2020.
Acknowledgements
The authors thank Muthuramakrishnan Venkitasubramaniam for the useful conversations and insights he provided, Tore Frederiksen for reviewing and confirming our cost analysis of his protocol [23], Peter Scholl and Xiao Wang for providing detailed cost analyses of their respective protocols [30, 49], and Nigel Smart for pointing out the connection to Residue Number Systems. This research was supported in part by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Project Activity (IARPA) under contract number 2019-19-020700009 (ACHILLES). The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of ODNI, IARPA, DoI/NBC, or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Nigel Smart.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A preliminary version [9] of this work appeared in CRYPTO 2020.
Appendices
Appendix A. The UC Model and Useful Functionalities
1.1 Appendix A.1. Universal Composability
We give a high-level overview of the UC model and refer the reader to [7] for a further details.
The real-world experiment involves n parties \(\mathcal{P} _1,\ldots ,\mathcal{P} _n\) that execute a protocol \(\pi _{\mathsf {}} {}\), an adversary \(\mathcal{A} \) that can corrupt a subset of the parties, and an environment \(\mathcal{Z} \) that is initialized with an advice-string z. All entities are initialized with the security parameter \({\kappa } \) and with a random tape. The environment activates the parties involved in \(\pi _{\mathsf {}} {}\), chooses their inputs and receives their outputs, and communicates with the adversary \(\mathcal{A} \). A semi-honest adversary simply observes the memory of the corrupted parties, while a malicious adversary may instruct them to arbitrarily deviate from \(\pi _{\mathsf {}} {}\). In this work, we consider only static adversaries, who corrupt up to \(n-1\) parties at the beginning of the experiment. The real-world experiment completes when \(\mathcal{Z} \) stops activating parties and outputs a decision bit. Let \({{\textsc {real}}}_{\pi _{\mathsf {}} {}, \mathcal{A}, \mathcal{Z}}(z,{\kappa })\) denote the random variable representing the output of the experiment.
The ideal-world experiment involves n dummy parties \(\mathcal{P} _1,\ldots ,\mathcal{P} _n\), an ideal functionality \({\mathcal {F}}_{\mathsf {}} {}\), an ideal-world adversary \(\mathcal{S} \) (the simulator), and an environment \(\mathcal{Z} \). The dummy parties act as routers that forward any message received from \(\mathcal{Z} \) to \({\mathcal {F}}_{\mathsf {}} {}\) and vice versa. The simulator can corrupt a subset of the dummy parties and interact with \({\mathcal {F}}_{\mathsf {}} {}\) on their behalf; in addition, \(\mathcal S\) can communicate directly with \({\mathcal {F}}_{\mathsf {}} {}\) according to its specification. The environment and the simulator can interact throughout the experiment, and the goal of the simulator is to trick the environment into believing it is running in the real experiment. The ideal-world experiment completes when \(\mathcal{Z} \) stops activating parties and outputs a decision bit. Let \({{\textsc {ideal}}}_{{\mathcal {F}}_{\mathsf {}} {},\mathcal{S}, \mathcal{Z}}(z,{\kappa })\) denote the random variable representing the output of the experiment.
A protocol \(\pi _{\mathsf {}} {}\) UC-realizes a functionality \({\mathcal {F}}_{\mathsf {}} {}\) if for every probabilistic polynomial-time (PPT) adversary \(\mathcal{A} \) there exists a PPT simulator \(\mathcal{S} \) such that for every PPT environment \(\mathcal{Z} \)
If the above distributions are perfectly or statistically indistinguishable, then we say that \(\pi _{\mathsf {}} {}\) perfectly or statistically UC-realizes \({\mathcal {F}}_{\mathsf {}} {}\), respectively.
Communication model. We follow standard practice of MPC protocols: Every pair of parties can communicate via an authenticated channel, and in the malicious setting we additionally assume the existence of a broadcast channel. Formally, the protocols are defined in the \(({\mathcal {F}}_{\mathsf {auth}},{\mathcal {F}}_{\mathsf {bc}})\)-hybrid model (see [7, 8]). We leave this implicit in their descriptions.
1.2 Appendix A.2. Useful Functionalities
To realize  and
and  , we use a number of standard functionalities that have well-known realizations in the cryptography literature. For completeness, we give those functionalities in this section. First among them is a simple distributed coin-tossing functionality, which samples an element uniformly at random from an arbitrary domain.
, we use a number of standard functionalities that have well-known realizations in the cryptography literature. For completeness, we give those functionalities in this section. First among them is a simple distributed coin-tossing functionality, which samples an element uniformly at random from an arbitrary domain.

We also make use of a one-to-many commitment functionality, which we have taken directly from Canetti et al. [8].

In  (Protocol 5.2), we make use of a functionality for randomly sampling integer shares of zero. This functionality can be realized assuming two-party coin tossing via a slight modification of a protocol of Cramer et al. [17].
(Protocol 5.2), we make use of a functionality for randomly sampling integer shares of zero. This functionality can be realized assuming two-party coin tossing via a slight modification of a protocol of Cramer et al. [17].

In both  and
and  , we use a functionality for generic commit-and-compute multiparty computation. This functionality allows each party to commit to private inputs, after which the parties agree on one or more arbitrary circuits to apply to those inputs. It can be realized using many generic multiparty computation protocols.
, we use a functionality for generic commit-and-compute multiparty computation. This functionality allows each party to commit to private inputs, after which the parties agree on one or more arbitrary circuits to apply to those inputs. It can be realized using many generic multiparty computation protocols.

Finally, we use a delayed-transmission correlated oblivious transfer functionality as the basis of our multiplication protocols. This functionality can be realized by combining a standard OT protocol with a commitment scheme, as we discuss in Appendix B.1. Unlike an ordinary COT functionality, which allows the sender to associate a single correlation to each choice bit, this functionality allows the sender to associate an arbitrary number of correlations to each bit. The transfer action then commits the sender to the correlations, and the sender can later decommit them individually, at which point the receiver learns either a random pad, or the same pad plus the decommitted correlation, according to their choice. We suggest that this functionality be instantiated via either Silent OT-extension [6] or the KOS OT-extension protocol [35].

Appendix B. Instantiating Multiplication
In this section, we describe how to instantiate the  functionality and discuss the efficiency of our protocols. In Appendix B.1, we begin by using oblivious transfer and commitments to build delayed correlated oblivious transfer (
functionality and discuss the efficiency of our protocols. In Appendix B.1, we begin by using oblivious transfer and commitments to build delayed correlated oblivious transfer ( ). In Appendix B.2, we use
). In Appendix B.2, we use  to realize a two-party multiplier
to realize a two-party multiplier  that allows inputs to be reused and postpones the detection of malicious behavior. In Appendix B.3, we plug this into the classic GMW multiplication technique [26] in order to realize an n-party multiplier
that allows inputs to be reused and postpones the detection of malicious behavior. In Appendix B.3, we plug this into the classic GMW multiplication technique [26] in order to realize an n-party multiplier  , with the same properties of input-reuse and delayed cheat detection. Finally, in Appendix B.4, we combine this component with generic multiparty computation (
, with the same properties of input-reuse and delayed cheat detection. Finally, in Appendix B.4, we combine this component with generic multiparty computation ( ) via a simple MAC to realize
) via a simple MAC to realize  . We discuss security and give concrete efficiency analysis in parallel. In our efficiency analysis, we make the same assumptions and concessions as in Sect. 6.
. We discuss security and give concrete efficiency analysis in parallel. In our efficiency analysis, we make the same assumptions and concessions as in Sect. 6.
1.1 Appendix B.1. Delayed-Transmission Correlated Oblivious Transfer
Given groups \({\mathbb {G}}_1,\ldots ,{\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\), the functionality  with respect to \({\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\) can be realized in the
with respect to \({\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\) can be realized in the  -hybrid model, where
-hybrid model, where  is the standard oblivious-transfer functionality [8]. Our construction uses a collection of \({\ell _\mathsf {\scriptscriptstyle OT}}\) hash functions \(H_i:\{0,1\}^{\lambda } \rightarrow {\mathbb {G}}_i\) such that for \(r\leftarrow \{0,1\}^{\lambda } \), the vector \((H_1(r),\ldots ,H_{\ell _\mathsf {\scriptscriptstyle OT}}(r))\) is indistinguishable from \((g_1,\ldots ,g_{\ell _\mathsf {\scriptscriptstyle OT}})\leftarrow {\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\). This is trivial when each \(H_i\) is modeled as a random oracle.
is the standard oblivious-transfer functionality [8]. Our construction uses a collection of \({\ell _\mathsf {\scriptscriptstyle OT}}\) hash functions \(H_i:\{0,1\}^{\lambda } \rightarrow {\mathbb {G}}_i\) such that for \(r\leftarrow \{0,1\}^{\lambda } \), the vector \((H_1(r),\ldots ,H_{\ell _\mathsf {\scriptscriptstyle OT}}(r))\) is indistinguishable from \((g_1,\ldots ,g_{\ell _\mathsf {\scriptscriptstyle OT}})\leftarrow {\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\). This is trivial when each \(H_i\) is modeled as a random oracle.
-
1.
The sender samples two uniformly random messages \((r_0,r_1)\leftarrow \{0,1\}^{{\lambda }}\times \{0,1\}^{{\lambda }}\), and the receiver (who has an input bit \(\beta \in \{0,1\}\)) uses
 to receive \(r_\beta \).
to receive \(r_\beta \). -
2.
In order to commit to its input-correlation vector \({\varvec{\mathrm {\alpha }}}\), the sender sends \({\varvec{\mathrm {\alpha }}}_i-H_i(r_0)-H_i(r_1)\) for \(i\in [{\ell _\mathsf {\scriptscriptstyle OT}}]\) to
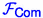 .
. -
3.
The sender and receiver use
 to sample an agreed-upon uniform vector \(\tilde{{\varvec{\mathrm {\rho }}}}\leftarrow {\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\). The sender outputs \({\varvec{\mathrm {\rho }}}:=\{H_i(r_0)+H_i({\varvec{\mathrm {\alpha }}}_i-H_i(r_0)-H_i(r_1))-\tilde{{\varvec{\mathrm {\rho }}}}_i\}_{i\in [{\ell _\mathsf {\scriptscriptstyle OT}}]}\) as its pads.
to sample an agreed-upon uniform vector \(\tilde{{\varvec{\mathrm {\rho }}}}\leftarrow {\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\). The sender outputs \({\varvec{\mathrm {\rho }}}:=\{H_i(r_0)+H_i({\varvec{\mathrm {\alpha }}}_i-H_i(r_0)-H_i(r_1))-\tilde{{\varvec{\mathrm {\rho }}}}_i\}_{i\in [{\ell _\mathsf {\scriptscriptstyle OT}}]}\) as its pads. -
4.
To implement the transfer instruction for index i, the sender instructs
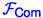 to decommit \(x\equiv {\varvec{\mathrm {\alpha }}}_i-H_i(r_0)-H_i(r_1)\), and then the receiver retrieves its output follows:
to decommit \(x\equiv {\varvec{\mathrm {\alpha }}}_i-H_i(r_0)-H_i(r_1)\), and then the receiver retrieves its output follows:-
If \(\beta =0\), then the receiver calculates its output as \(\tilde{{\varvec{\mathrm {\rho }}}}_i-H_i(r_0)-H_i(x)\). Note that this is equivalent to \(-{\varvec{\mathrm {\rho }}}_i\)
-
If \(\beta =1\), then the receiver calculates its output as \(x + \tilde{{\varvec{\mathrm {\rho }}}}_i+H_i(r_1)-H_i(x)\). Note that this is equivalent to \({\varvec{\mathrm {\alpha }}}_i-{\varvec{\mathrm {\rho }}}_i\).
-
It is clear to see that at the end of this protocol, the sender and receiver hold additive shares of \(\beta \cdot {\varvec{\mathrm {\alpha }}}_i\) for every index i that has been decommitted, and that the sender is committed to \({\varvec{\mathrm {\alpha }}}\).
Theorem B.1
Let \({\mathbb {G}}_1,\ldots ,{\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\) be groups and assume there exists a collection \(\{H_i:\{0,1\}^{\lambda } \rightarrow {\mathbb {G}}_i\}_{i\in [{\ell _\mathsf {\scriptscriptstyle OT}}]}\) as described above. Then, there exists a protocol in the  ,
, -hybrid model that UC-realizes
-hybrid model that UC-realizes  with respect to \({\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\) against a malicious PPT adversary that statically corrupts one party, and this protocol requires a single invocation of
with respect to \({\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\) against a malicious PPT adversary that statically corrupts one party, and this protocol requires a single invocation of  .
.
We note that with a particular usage pattern, there is a more efficient instantiation available, based upon a non-black-box usage of either Silent OT [6] or KOS OT [35], which we introduced in Sect. 6.2. In particular, assume there is some specific point in time, and that all correlations are decommitted either immediately after they are committed, or at that point. Both Silent OT and KOS OT involve sending a message from the receiver to the sender first, followed by a message from the sender to the receiver, where each bit in this latter message corresponds to one bit of the correlation(s) transferred (and any correlation bit can be recovered from only the one associated message bit). Thus,  can be realized in the following context-optimized way: the receiver sends its message, and then the sender sends the bits of its message associated with the correlations to be immediately released, and commits (using a single commitment) to the other bits of its message. These bits are decommitted later. This eliminates the potential overhead associated with transferring the \(r_0\) and \(r_1\) values in our above construction. Furthermore, if many
can be realized in the following context-optimized way: the receiver sends its message, and then the sender sends the bits of its message associated with the correlations to be immediately released, and commits (using a single commitment) to the other bits of its message. These bits are decommitted later. This eliminates the potential overhead associated with transferring the \(r_0\) and \(r_1\) values in our above construction. Furthermore, if many  instances are invoked at once, and the delayed-release correlations are released simultaneously across all instances, then the instances can share a single commitment. Our usage of
instances are invoked at once, and the delayed-release correlations are released simultaneously across all instances, then the instances can share a single commitment. Our usage of  matches this pattern, and so its cost is equal (up to a few bits) to that of either Silent OT or KOS OT. When calculating concrete efficiency figures, we assume the overhead is exactly zero.
matches this pattern, and so its cost is equal (up to a few bits) to that of either Silent OT or KOS OT. When calculating concrete efficiency figures, we assume the overhead is exactly zero.
1.2 B.2. Two-Party Reusable-Input Multiplier
Our basic two-party multiplication functionality  allows parties to input arbitrarily many values, whereafter, on request, it returns additive shares of the product of any pair of them. Unlike the standard two-party multiplication functionality, however, we allow the adversary to both request the honest party’s inputs and determine the output products. We then add two explicit check commands which the parties can agree to invoke. One notifies the honest party if the adversary has used its power to cheat, and the other opens the private inputs to the multiplication, while also, as a side effect, notifying the honest party if the adversary has used its power to cheat.
allows parties to input arbitrarily many values, whereafter, on request, it returns additive shares of the product of any pair of them. Unlike the standard two-party multiplication functionality, however, we allow the adversary to both request the honest party’s inputs and determine the output products. We then add two explicit check commands which the parties can agree to invoke. One notifies the honest party if the adversary has used its power to cheat, and the other opens the private inputs to the multiplication, while also, as a side effect, notifying the honest party if the adversary has used its power to cheat.

Theorem B.3
There exists a protocol in the  -hybrid model that statistically UC-realizes
-hybrid model that statistically UC-realizes  against a malicious adversary that statically corrupts one party.
against a malicious adversary that statically corrupts one party.
The proof of this theorem is via construction of a protocol  , which we sketch here, along with a security argument. We adapt the multiplication protocols of Doerner et al., and refer the reader to their work [20, Section 3] for a more in-depth technical explanation. Our main changes involve making the security parameter independent of the working field, separating the input, multiplication, and cheater check components into separate phases such that inputs can be reused and checks performed retroactively, and adding an input-opening phase not originally present. For any input the parties can choose to use either the cheater check or the input-opening mechanism, but not both. Along with the sketch of each phase of the protocol, we provide a cost analysis of that phase, and sketch a simulation strategy and security argument. We omit a formal proof of security via hybrid experiments, as it would closely resemble proofs already provided by Doerner et al. [19, 20].
, which we sketch here, along with a security argument. We adapt the multiplication protocols of Doerner et al., and refer the reader to their work [20, Section 3] for a more in-depth technical explanation. Our main changes involve making the security parameter independent of the working field, separating the input, multiplication, and cheater check components into separate phases such that inputs can be reused and checks performed retroactively, and adding an input-opening phase not originally present. For any input the parties can choose to use either the cheater check or the input-opening mechanism, but not both. Along with the sketch of each phase of the protocol, we provide a cost analysis of that phase, and sketch a simulation strategy and security argument. We omit a formal proof of security via hybrid experiments, as it would closely resemble proofs already provided by Doerner et al. [19, 20].
Common parameters and hybrid functionalities. The protocol  is parametrized by the statistical security parameter \({s} \) and a prime \(m\) such that \(|m|\in O(\log {s})\). For convenience, we define a batch-size \({\xi } :=2{s} + |m|\) and a repetition count \(r=\left\lceil {s}/|m| \right\rceil \). Looking ahead, Bob will encode his input via the inner product of \({\xi } \) random bits and a uniformly sampled vector \({\varvec{\mathrm {g}}}\). Intuitively, the parameter \({\xi } \) is set so that even if \({s} \) bits of his codeword are revealed to Alice, she has negligible advantage in guessing his input. Note that unlike in prior works, \({\varvec{\mathrm {g}}}\) is not fixed ahead of time, but chosen uniformly after Alice is committed to her inputs. The participating parties have access to the coin-tossing functionality
is parametrized by the statistical security parameter \({s} \) and a prime \(m\) such that \(|m|\in O(\log {s})\). For convenience, we define a batch-size \({\xi } :=2{s} + |m|\) and a repetition count \(r=\left\lceil {s}/|m| \right\rceil \). Looking ahead, Bob will encode his input via the inner product of \({\xi } \) random bits and a uniformly sampled vector \({\varvec{\mathrm {g}}}\). Intuitively, the parameter \({\xi } \) is set so that even if \({s} \) bits of his codeword are revealed to Alice, she has negligible advantage in guessing his input. Note that unlike in prior works, \({\varvec{\mathrm {g}}}\) is not fixed ahead of time, but chosen uniformly after Alice is committed to her inputs. The participating parties have access to the coin-tossing functionality  , the commitment functionality
, the commitment functionality  , and the delayed-transfer COT functionality
, and the delayed-transfer COT functionality  .
.
The Input and Multiplication phases of
 . For the sake of succinctness, we will describe the input and multiplication processes jointly: each party will supply exactly one input, and they will receive shares of the product, in a single step. Later, we will discuss how the protocol can be generalized to allow the parties to input values independently, and to reuse those input values. Alice begins the protocol with an input \(a\in [0,m)\), and Bob with an input \(b\in [0,m)\), and they both know a fresh, agreed-upon session ID \(\mathsf {sid}\). They take the following steps:
. For the sake of succinctness, we will describe the input and multiplication processes jointly: each party will supply exactly one input, and they will receive shares of the product, in a single step. Later, we will discuss how the protocol can be generalized to allow the parties to input values independently, and to reuse those input values. Alice begins the protocol with an input \(a\in [0,m)\), and Bob with an input \(b\in [0,m)\), and they both know a fresh, agreed-upon session ID \(\mathsf {sid}\). They take the following steps:

While the correctness of the above procedure is easy to verify when both parties follow the protocol, we note that it omits some of the consistency-check components of the protocols of Doerner et al. [19, 20], which will appear in the next protocol phase. In particular, the consistency-check vector \({{\tilde{\mathbf{a}}}}\) is committed by the end of the protocol, but it has not yet been transferred to Bob. This omission admits cheating behavior, such as a corrupt Alice using different values for \(a\) in each iteration of Step 4b. We model these attacks in  by allowing the ideal adversary to fully control the results of a multiplication, once it has explicitly notified
by allowing the ideal adversary to fully control the results of a multiplication, once it has explicitly notified  that it wishes to cheat.
that it wishes to cheat.
If the parties agree that Alice should be compelled to reuse an input in multiple different multiplications, then she must also reuse the same consistency-check vector \({{\tilde{\mathbf{a}}}}\) in all of those multiplications. The consistency-check mechanism (in the next protocol phase) that ensures the internal consistency of a single multiplication will also ensure the consistency of many multiplications.
If the parties agree that Bob should be compelled to reuse an input in multiple different multiplications, then the above protocol is run exactly once, and Alice combines her inputs for all of those multiplications (and their associated, independent consistency-check vectors) into a single array, which she commits to in Step 4b. She then repeats Step 4c, changing the index as appropriate to cause the transfer of each of her inputs (but not, for now, the consistency-check vectors). The remaining steps in the protocol are repeated once for each multiplication, except for Step 8, which is performed exactly once, for Bob’s one input.
In the case that Bob wishes to input a value to be used in one or more later (potentially dynamically chosen) multiplications, the parties can run the above protocol until Step 4a is complete and then pause the protocol until a multiplication using Bob’s input must be performed. In the case that Alice wishes to input a value to be used later, Bob must input a dummy value, and compulsory input reuse is employed (as previously described) to ensure she uses her input again in the appropriate multiplications, when they occur.
We observe that the dominant cost of the above protocol is incurred by the \({\xi } =2s+|m|\) invocations of  per multiplication, each invocation with a correlation of size \(|m|\). If we realize
per multiplication, each invocation with a correlation of size \(|m|\). If we realize  via Silent OT, then Alice must transmit \(|m|\cdot (|m|+2{s})+4{\lambda } \) bits in total and Bob must transmit \(2|m|+2{s} \) bits it total. If we realize
via Silent OT, then Alice must transmit \(|m|\cdot (|m|+2{s})+4{\lambda } \) bits in total and Bob must transmit \(2|m|+2{s} \) bits it total. If we realize  via KOS OT, then Alice must transmit \(|m|\cdot (|m|+2{s})+4{\lambda } \) bits in total and Bob must transmit \({\lambda } \cdot (|m|+2{s})+|m|\) bits in total. Regardless, they require three rounds if
via KOS OT, then Alice must transmit \(|m|\cdot (|m|+2{s})+4{\lambda } \) bits in total and Bob must transmit \({\lambda } \cdot (|m|+2{s})+|m|\) bits in total. Regardless, they require three rounds if  is realized non-interactively.
is realized non-interactively.
Simulator overview. Since our multiplication protocol has two asymmetric roles, we specify two separate simulation strategies: one against a corrupted Alice, and the other against a corrupted Bob. As in prior malicious-secure OT-based multipliers, Bob has few avenues via which he can cheat, and so his simulator is relatively straightforward. On the other hand, the division of the protocol into multiple independent phases and addition of a second cheater-checking mechanism has noticeably complicated simulation against Alice. Alice is committed to her inputs and to many components of the cheater-check mechanisms by the end of the input/multiplication phase. The simulation can thus analyze her cheats before returning an output to her. Based on certain attributes of her cheats, the simulator may decide to call the \(\texttt {cheat}\) interface of  , in which case the functionality will certainly abort when either the cheater check or input revelation phases is called, or the simulator may decide to avoid calling the \(\texttt {cheat}\) interface (thereby depriving the adversary of leakage and control over the output), and instead manually instruct
, in which case the functionality will certainly abort when either the cheater check or input revelation phases is called, or the simulator may decide to avoid calling the \(\texttt {cheat}\) interface (thereby depriving the adversary of leakage and control over the output), and instead manually instruct  to abort when one or both of the aforementioned phases is actually entered, or the simulator may not abort at all.
to abort when one or both of the aforementioned phases is actually entered, or the simulator may not abort at all.
Simulating Inputs and Multiplication. Simulation of this phase against a corrupt Bob is simple: he has no avenue for cheating, and his ideal input in any single instance of the above protocol is defined by \(b\equiv \delta +\langle {\varvec{\mathrm {g}}}, {\varvec{\mathrm {\beta }}} \rangle \pmod {m}\), which is available to the simulator. The only values that he receives during the course of the protocol are \({\varvec{\mathrm {g}}}\) and \({\varvec{\mathrm {z}}}_{{{\mathsf {B}}},*}\), which can be simulated by sampling them uniformly.
Simulating against a corrupt Alice is more involved: if she uses inconsistent values of \(a\) across the OT instances in Step 4b, then the simulator takes her most common value to be her ideal input (breaking ties arbitrarily). Let this ideal input be denoted by \(a\), and let the vector of (possibly inconsistent) she supplied in the OT instances be \({\varvec{\mathrm {\alpha }}}\). The length \({\varvec{\mathrm {\alpha }}}\) depends upon the number of multiplications in which Alice and Bob agreed that her input should be reused; for example \(|{\varvec{\mathrm {\alpha }}}|={\xi } \) if \(a\) was used in only one multiplication. Without loss of generality, we will assume one multiplication only for the rest of our simulator description, but note where generalizations must occur. Let c be the number of inconsistencies in \({\varvec{\mathrm {\alpha }}}\) with respect to \(a\), and let \({\varvec{\mathrm {I}}}\) be a vector of the indices of these inconsistencies; that is, a vector such that \(|{\varvec{\mathrm {I}}}|=c\) and \(\forall i\in [|{\varvec{\mathrm {\alpha }}}|], {\varvec{\mathrm {\alpha }}}_i \ne a\iff i\in {\varvec{\mathrm {I}}}\). We have two cases.
If \(c \ge {s} \), then the simulator activates the \(\texttt {cheat}\) interface of  and receives Bob’s inputs. Hereafter, the simulator can run Bob’s code in order to behave exactly as he would in the real world. Since neither the real Bob nor the
and receives Bob’s inputs. Hereafter, the simulator can run Bob’s code in order to behave exactly as he would in the real world. Since neither the real Bob nor the  aborts during the input and multiplication phases, regardless of Alice’s behavior, it is easy to see that the real and ideal world experiments are identically distributed insofar as those two phases are concerned. However, activating the \(\texttt {cheat}\) interface dooms
aborts during the input and multiplication phases, regardless of Alice’s behavior, it is easy to see that the real and ideal world experiments are identically distributed insofar as those two phases are concerned. However, activating the \(\texttt {cheat}\) interface dooms  to abort when the input-opening or cheater-check interfaces are used, and so it remains to prove that Bob aborts with overwhelming probability in the real word when the corresponding protocol phases are run. We will discuss this further in the relevant sections.
to abort when the input-opening or cheater-check interfaces are used, and so it remains to prove that Bob aborts with overwhelming probability in the real word when the corresponding protocol phases are run. We will discuss this further in the relevant sections.
If \(c < {s} \), then the simulator will not call the \(\texttt {cheat}\) interface of  , but will instead use the same interface as an honest Alice, compute and apply the effects of Alice’s inconsistencies locally, and potentially instruct
, but will instead use the same interface as an honest Alice, compute and apply the effects of Alice’s inconsistencies locally, and potentially instruct  to abort at a later time. The simulator begins by sampling \({\varvec{\mathrm {g}}}\leftarrow \smash {{\mathbb {Z}}_m^{|{\varvec{\mathrm {\alpha }}}|}}\) uniformly. It then computes a vector \({\varvec{\mathrm {\Delta }}}\) of the offsets by which Alice has cheated, one for each OT instance,
to abort at a later time. The simulator begins by sampling \({\varvec{\mathrm {g}}}\leftarrow \smash {{\mathbb {Z}}_m^{|{\varvec{\mathrm {\alpha }}}|}}\) uniformly. It then computes a vector \({\varvec{\mathrm {\Delta }}}\) of the offsets by which Alice has cheated, one for each OT instance,
after which it flips a coin for each location where Alice has cheated. That is, if we let \(\hat{{\varvec{\mathrm {\beta }}}}\) represent the simulator’s coins, then it samples \(\hat{{\varvec{\mathrm {\beta }}}}_i\leftarrow \{0,1\}\) for \(i\in {\varvec{\mathrm {I}}}\) and sets \(\hat{{\varvec{\mathrm {\beta }}}}_i:=\bot \) (where \(\bot \) is a special symbol indicating that no value has been chosen) otherwise.
Next, the simulator calls the input phase of  using \(a\) as its input value, and then, for each time that the input \(\varvec{\alpha }\) is supposed to be reused, it performs the following sequence of steps. First, it calls the multiply phase of
using \(a\) as its input value, and then, for each time that the input \(\varvec{\alpha }\) is supposed to be reused, it performs the following sequence of steps. First, it calls the multiply phase of  , and receives \({\hat{z}}_{{\mathsf {A}}} \) as output. In order to deliver a reply to Alice on behalf of
, and receives \({\hat{z}}_{{\mathsf {A}}} \) as output. In order to deliver a reply to Alice on behalf of  in Step 4b of the protocol, the simulator must apply Alice’s cheats. It samples a uniform \(\delta \leftarrow {\mathbb {Z}}_m\) and a set of ideal outputs for the OT instances; specifically, it finds a vector \(\smash {\hat{{\varvec{\mathrm {z}}}}_{{{\mathsf {A}}},*}\in {\mathbb {Z}}_m^{{\xi }}}\) such that
in Step 4b of the protocol, the simulator must apply Alice’s cheats. It samples a uniform \(\delta \leftarrow {\mathbb {Z}}_m\) and a set of ideal outputs for the OT instances; specifically, it finds a vector \(\smash {\hat{{\varvec{\mathrm {z}}}}_{{{\mathsf {A}}},*}\in {\mathbb {Z}}_m^{{\xi }}}\) such that
and using these values, the simulator computes the values that it must output to Alice on behalf of  :
:
Here again we have assumed that \(a\) is being used in only one multiplication, and so \(|{\varvec{\mathrm {\alpha }}}|=|\hat{{\varvec{\mathrm {\beta }}}}|=|{\varvec{\mathrm {\Delta }}}|={\xi } \); in generality, the simulator uses the appropriate slice of \({\varvec{\mathrm {\Delta }}}\) and \(\hat{{\varvec{\mathrm {\beta }}}}\) for each multiplication, and then concatenates the resulting vectors to form one unified vector \(\smash {{\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\in {\mathbb {Z}}_m^{|{\varvec{\mathrm {\alpha }}}|}}\). To simulate Step 4b of the protocol, the simulator sends each \(\smash {{\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i}}\) to Alice on behalf of the \(i^\text {th}\) instance of  .
.
In Step 6 of the protocol, the simulator receives \((a',{\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*})\) and \(({\varvec{\mathrm {\zeta }}},{\varvec{\mathrm {\psi }}})\) from Alice on behalf of  . Note that if Alice is honest, then \(a=a'\) and \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}={\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*}\), but in general Alice might cheat, and so these values are stored by the simulator for later. To simulate Step 7, the simulator sends \({\varvec{\mathrm {g}}}\) on behalf of
. Note that if Alice is honest, then \(a=a'\) and \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}={\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*}\), but in general Alice might cheat, and so these values are stored by the simulator for later. To simulate Step 7, the simulator sends \({\varvec{\mathrm {g}}}\) on behalf of  , which it previously sampled uniformly just as
, which it previously sampled uniformly just as  would. To simulate Step 8 of the protocol, the simulator sends the value \(\delta \) that it sampled previously to Alice on behalf of Bob. This completes the simulation for the input and multiplication phases of
would. To simulate Step 8 of the protocol, the simulator sends the value \(\delta \) that it sampled previously to Alice on behalf of Bob. This completes the simulation for the input and multiplication phases of  against a corrupt Alice, when \(c < {s} \).
against a corrupt Alice, when \(c < {s} \).
We will briefly argue for the indistinguishability of the real and ideal-world experiments with respect to adversaries corrupting Alice, when \(c<{s} \). The adversary’s view includes \({\varvec{\mathrm {\alpha }}}\), \(\delta \), \({\varvec{\mathrm {g}}}\), and \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\), and additionally, the environment determines the input \(b\) and receives the output \(z_{{\mathsf {B}}} \). We must analyze the joint distribution of these six variables. In both the real and ideal worlds, \({\varvec{\mathrm {g}}}\) is chosen uniformly and independently. In the ideal world, \(\delta \) is chosen uniformly and independently, but in the real world, it is chosen as the difference between \(b\) and the inner product of \({\varvec{\mathrm {g}}}\) and Bob’s choice bits \({\varvec{\mathrm {\beta }}}\). These two distributions are statistically indistinguishable as previously shown by Impagliazzo and Naor [31, Proposition 1.1] (see also [20, Lemma B.5]). Finally, in the ideal world, \(z_{{\mathsf {B}}} \) and \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) are chosen uniformly by  and the simulator, subject to the following constraints
and the simulator, subject to the following constraints
assuming that \(|{\varvec{\mathrm {\alpha }}}|=|\smash {\hat{{\varvec{\mathrm {\beta }}}}}|=|{\varvec{\mathrm {\Delta }}}|={\xi } \), as before. Substituting Eq. 8 into 7, and the result into 6 yields
and rearranging, we have
In the real world, on the other hand, \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) and \({\varvec{\mathrm {z}}}_{{{\mathsf {B}}},*}\) are chosen uniformly by  subject to
subject to
which implies that
Now, recall that \({\tilde{b}}\equiv b-\delta \pmod {m}\) and \(\left\langle {\varvec{\mathrm {g}}},{\varvec{\mathrm {\beta }}}\right\rangle \equiv {\tilde{b}}\pmod {m}\), which allows us to rewrite Eq. 10 by adding a zero-sum term to the right hand side:
where we take \(a\) to be the most common element of \({\varvec{\mathrm {\alpha }}}\), as in the ideal world. Rearranging, we have
Observe that Eqs. 9 and 11 are identical except for the difference between Bob’s choice bits \({\varvec{\mathrm {\beta }}}\) and the simulator’s simulated choice bits \(\smash {\hat{{\varvec{\mathrm {\beta }}}}}\). In the real world, Bob samples \({\varvec{\mathrm {\beta }}}\) uniformly. In the ideal world, the simulator samples \(\smash {\hat{{\varvec{\mathrm {\beta }}}}}\) uniformly at every index i where \({\varvec{\mathrm {\alpha }}}_i\ne a\). Thus, the constraints under which \(z_{{\mathsf {B}}} \) and \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) are sampled are equivalent in the real and ideal worlds, and the two worlds are statistically indistinguishable when \(c<{s} \).
The Cheater Check phase of
 . In this phase of the protocol, the parties perform a process analogous to the consistency check in the multiplication protocols of Doerner et al. [20]. This reveals to the honest parties any cheats in the protocol phases described above. As we have previously noted, Bob does not have an opportunity to cheat; thus this check verifies only Alice’s behavior, via the consistency-check vectors \({{\tilde{\mathbf{a}}}}\), \({\varvec{\mathrm {\zeta }}}\) and \({\varvec{\mathrm {\psi }}}\), to which she is committed. In addition to the consistency-check vector, Alice begins the protocol with an input \(a\), and both parties know a vector \({\textsf {sids}}\) of all the multiplications in which Alice was expected to use this input, along with a vector \(\textsf {bit-sids}\) of the individual
. In this phase of the protocol, the parties perform a process analogous to the consistency check in the multiplication protocols of Doerner et al. [20]. This reveals to the honest parties any cheats in the protocol phases described above. As we have previously noted, Bob does not have an opportunity to cheat; thus this check verifies only Alice’s behavior, via the consistency-check vectors \({{\tilde{\mathbf{a}}}}\), \({\varvec{\mathrm {\zeta }}}\) and \({\varvec{\mathrm {\psi }}}\), to which she is committed. In addition to the consistency-check vector, Alice begins the protocol with an input \(a\), and both parties know a vector \({\textsf {sids}}\) of all the multiplications in which Alice was expected to use this input, along with a vector \(\textsf {bit-sids}\) of the individual  instances (over all of the multiplications associated with \({\textsf {sids}}\)) in which she was expected to commit \(\{a\}\Vert {{\tilde{\mathbf{a}}}}\). Bob begins with a vector of choice bits, \({\varvec{\mathrm {\beta }}}\), one bit for each entry in \(\textsf {bit-sids}\). We assume for the sake of simplicity that Bob was not expected to reuse his inputs. The parties take the following steps:
instances (over all of the multiplications associated with \({\textsf {sids}}\)) in which she was expected to commit \(\{a\}\Vert {{\tilde{\mathbf{a}}}}\). Bob begins with a vector of choice bits, \({\varvec{\mathrm {\beta }}}\), one bit for each entry in \(\textsf {bit-sids}\). We assume for the sake of simplicity that Bob was not expected to reuse his inputs. The parties take the following steps:
-
1.
For each \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\), Alice sends \((\texttt {transfer},\textsf {bit-sids}_i,j+1)\) to
 , and as a consequence, Bob receives \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}\) such that \(0\le {\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}<m\). Note that if Alice has behaved honestly, then per the specification of
, and as a consequence, Bob receives \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}\) such that \(0\le {\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}<m\). Note that if Alice has behaved honestly, then per the specification of  , it holds for all \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\) that $$\begin{aligned} {\tilde{\mathbf{z}}}_{{{\mathsf {A}}},i,j}+{\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}\equiv {\varvec{\mathrm {\beta }}}_i \cdot {{\tilde{\mathbf{a}}}}_{j}\pmod {m} \end{aligned}$$
, it holds for all \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\) that $$\begin{aligned} {\tilde{\mathbf{z}}}_{{{\mathsf {A}}},i,j}+{\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}\equiv {\varvec{\mathrm {\beta }}}_i \cdot {{\tilde{\mathbf{a}}}}_{j}\pmod {m} \end{aligned}$$ -
2.
Alice instructs
 to decommit \(({\varvec{\mathrm {\zeta }}},{\varvec{\mathrm {\psi }}})\).
to decommit \(({\varvec{\mathrm {\zeta }}},{\varvec{\mathrm {\psi }}})\). -
3.
Bob verifies that for each \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\),
$$\begin{aligned} {\varvec{\mathrm {\zeta }}}_{i,j} + {\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}+{\varvec{\mathrm {e}}}_j\cdot {\varvec{\mathrm {z}}}_{{{\mathsf {B}}},i}\equiv {\varvec{\mathrm {\beta }}}_i\cdot {\varvec{\mathrm {\psi }}}_{j}\pmod {m} \end{aligned}$$and if this relationship does not hold, then he aborts.
The cheater check costs only one round and \(2{s} \cdot (|m|+2{s})\cdot |{\textsf {sids}}|\) bits of transmitted data for Alice, where \(|{\textsf {sids}}|\) is the number of multiplications in which the input to be checked was used.
Simulating the Cheater Check.Notice that in the foregoing procedure, Bob learns nothing about \(\alpha \) or \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\); all values derived from these are masked by Alice using uniformly sampled one-time pads before being transmitted to him. Notice furthermore that every value in Bob’s check in Step 3 is known to or determined by the simulator. Thus, simulation against Bob is trivial: the simulator can send Bob exactly the message that causes his check to pass, and then send the appropriate \(\texttt {check}\) message to  .
.
As before, simulation against Alice is more involved. Although Alice was instructed to reuse the same r-length vector \({{\tilde{\mathbf{a}}}}\) for all OT instances involving \(a\) in Step 4b of the input phase, she could have cheated and used different vectors in some OT instances. Thus, let \(\tilde{{\varvec{\mathrm {\alpha }}}}\in {\mathbb {Z}}_m^{|{\varvec{\mathrm {\alpha }}}|\times r}\) represent her actual inputs to the OTs, where \(\tilde{{\varvec{\mathrm {\alpha }}}}_{i,*} = \tilde{{\varvec{\mathrm {\alpha }}}}_{i',*} = {{\tilde{\mathbf{a}}}}\) for all \(i,i'\in [|{\varvec{\mathrm {\alpha }}}|]\) if Alice is honest. Note that \(|{\varvec{\mathrm {\alpha }}}|=|\textsf {bit-sids}|\). Upon the decommitment instruction from Alice on behalf of  , the simulator performs the following check for all \(i\in [|{\varvec{\mathrm {\alpha }}}|]\):
, the simulator performs the following check for all \(i\in [|{\varvec{\mathrm {\alpha }}}|]\):
-
1.
Let \({\varvec{\mathrm {J}}}\subseteq [r]\) be a vector containing every index j where the following equalities do not both hold:
$$\begin{aligned} {\varvec{\mathrm {\psi }}}_j&\equiv (\tilde{{\varvec{\mathrm {\alpha }}}}_{i,j}+{\varvec{\mathrm {e}}}_j\cdot {\varvec{\mathrm {\alpha }}}_{i}) \pmod {m}\\ {\varvec{\mathrm {\zeta }}}_{i,j}&\equiv ({\tilde{\mathbf{z}}}_{{{\mathsf {A}}},i,j}+{\varvec{\mathrm {e}}}_j\cdot {\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i}) \pmod {m} \end{aligned}$$Note that if Alice has acted honestly then these equalities will always hold.
-
2.
Compute \({\varvec{\mathrm {\beta }}}^*\in {\mathbb {Z}}_m^r\) such that
$$\begin{aligned} {\varvec{\mathrm {\beta }}}^*_j\equiv \left\{ \begin{aligned}&\frac{{\varvec{\mathrm {\zeta }}}_{i,j} - ({\tilde{\mathbf{z}}}_{{{\mathsf {A}}},i,j}+{\varvec{\mathrm {e}}}_j\cdot {\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i})}{{\varvec{\mathrm {\psi }}}_j - (\tilde{{\varvec{\mathrm {\alpha }}}}_{i,j}+{\varvec{\mathrm {e}}}_j\cdot {\varvec{\mathrm {\alpha }}}_{i})}\pmod {m}&\hbox { if}\ j\in {\varvec{\mathrm {J}}}\\&\bot&\hbox { if}\ j\not \in {\varvec{\mathrm {J}}} \end{aligned}\right. \end{aligned}$$where \(\bot \) is a special symbol used to indicate no value, and an additional special symbol \(\infty \) is used to indicate an undefined value due to division by zero.
-
3.
If there exists any index \(j\in [r]\) such that \({\varvec{\mathrm {\beta }}}^*_{j}\not \in \{0,1,\bot \}\), or any pair \((j,j')\) such that \({\varvec{\mathrm {\beta }}}^*_{j},{\varvec{\mathrm {\beta }}}^*_{j'}\in \{0,1\}\wedge {\varvec{\mathrm {\beta }}}^*_{j} \ne {\varvec{\mathrm {\beta }}}^*_{j'}\), then immediately instruct
 to abort. If the simulator continues past this point, it must be the case that either \({\varvec{\mathrm {\beta }}}^*\in \{0,\bot \}^r\) or \({\varvec{\mathrm {\beta }}}^*\in \{1,\bot \}^r\). This means that there exists a set of choice bits that would cause Bob’s check to pass in the real world.
to abort. If the simulator continues past this point, it must be the case that either \({\varvec{\mathrm {\beta }}}^*\in \{0,\bot \}^r\) or \({\varvec{\mathrm {\beta }}}^*\in \{1,\bot \}^r\). This means that there exists a set of choice bits that would cause Bob’s check to pass in the real world. -
4.
If \(i\in {\varvec{\mathrm {I}}}\) and there exists an index \(j\in [r]\) such that \({\varvec{\mathrm {\beta }}}^*_j\not \in \{\hat{{\varvec{\mathrm {\beta }}}}_i,\bot \}\), then immediately instruct
 to abort.
to abort. -
5.
If \(i\not \in {\varvec{\mathrm {I}}}\) and there exists an index \(j\in [r]\) such that \({\varvec{\mathrm {\beta }}}^*_j \ne \bot \), then flip a uniform coin and immediately instruct
 abort if it lands on heads.
abort if it lands on heads.
If the check passes (i.e., no abort instruction is issued) for all \(i\in [|{\varvec{\mathrm {\alpha }}}|]\), then the simulator sends the appropriate \(\texttt {check}\) message to  (which will abort at this point if the \(\texttt {cheat}\) instruction was previously issued), completing the simulation.
(which will abort at this point if the \(\texttt {cheat}\) instruction was previously issued), completing the simulation.
We will briefly argue for indistinguishability of the real and ideal-world experiments, with respect to adversaries corrupting Alice. During this phase, no values are transmitted to Alice, and thus the two worlds are distinguishable only by the distribution of aborts. In the real world, Bob aborts unless
for every \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\), per Step 3 of the protocol, and if we take \(a\) to be the most common input among Alice’s OT instances (breaking ties arbitrarily) and \({\varvec{\mathrm {\Delta }}}\) to be a vector of deviations from \(a\), then, rewriting, we have
On the other hand, in the ideal world, there are a number of abort conditions. We will argue that for every condition that triggers an abort in the ideal world, an abort is also observed by Alice in the real world with negligibly different probability.
-
1.
The abort condition in Step 3 of the simulator checks whether there exists any hypothetical set of choice bits that could allow Eq. 12 to hold, given Alice’s messages. If no such set of choice bits exists, then the simulator aborts, and clearly Bob must abort in the real world as well.
-
2.
The abort condition in Steps 4 and 5 of the simulator checks whether Eq. 12 holds, given a simulated set of Bob’s choice bits. The condition is split into two cases to ensure these choice bits are consistent with any simulated choice bits previously sampled when simulating the multiplication phase of the protocol, which the environment may have been able to infer from the outputs \(z_{{\mathsf {B}}} \) and \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) that it receives at the end of the multiplication phase. Regardless, the simulated choice bits are chosen uniformly in the ideal world after Alice is already committed to \({\varvec{\mathrm {\zeta }}}\) and \({\varvec{\mathrm {\psi }}}\), and the real choice bits are chosen uniformly by Bob and information-theoretically hidden from Alice until after her commitments are made, and thus the probability of abort is the same in both worlds. Notice that this case technically subsumes the first.
-
3.
The abort condition in the cheater check phase of
 is triggered at the end of the simulation if and only if \(c\ge {s} \), which implies the vector \({\varvec{\mathrm {\Delta }}}\) is nonzero (i.e., Alice cheated when supplying inputs to
is triggered at the end of the simulation if and only if \(c\ge {s} \), which implies the vector \({\varvec{\mathrm {\Delta }}}\) is nonzero (i.e., Alice cheated when supplying inputs to  ) at at least \(s\) locations. We argue that under this condition, Bob aborts with overwhelming probability in the real world as well.
) at at least \(s\) locations. We argue that under this condition, Bob aborts with overwhelming probability in the real world as well.
Notice first that Alice commits to \({\varvec{\mathrm {\alpha }}}\) and \(\tilde{{\varvec{\mathrm {\alpha }}}}\) before \({\varvec{\mathrm {e}}}\) is defined. After receiving \({\varvec{\mathrm {e}}}\), she commits to \({\varvec{\mathrm {\zeta }}}\) and \({\varvec{\mathrm {\psi }}}\), and only then does she receive \(\delta \) (and the environment receives \(z_{{\mathsf {B}}} \)), which might potentially allow \({\varvec{\mathrm {\beta }}}\) to be distinguished from uniform.
Consider Bob’s real-world check, Eq. 12. Since Alice knows every value on the left-hand side, and is permitted to freely choose \({\varvec{\mathrm {\zeta }}}_{i,j}\) after learning the others, the left-hand side is completely within her control. Now consider some index j and two indices i, \(i'\) such that \({\varvec{\mathrm {\Delta }}}_i\ne {\varvec{\mathrm {\Delta }}}_{i'}\). Due to the order in which values are committed and sampled, we have
regardless of how Alice samples her variables (again, assuming \({\varvec{\mathrm {\Delta }}}_i\ne {\varvec{\mathrm {\Delta }}}_{i'}\)). Over r independent repetitions, the probability that the above equality holds is \(1/m^r \le 2^{-{s}}\), and it follows that if there exists any pair of indices i and \(i'\) such that \({\varvec{\mathrm {\Delta }}}_i\ne {\varvec{\mathrm {\Delta }}}_{i'}\), then with probability overwhelming in \({s} \) there exists some index j such that
Without loss of generality, then, let us say that the left-hand predicate holds. Since \({\varvec{\mathrm {\beta }}}_i\in \{0,1\}\) is uniformly sampled and information-theoretically hidden from Alice at the time she commits to \({\varvec{\mathrm {\zeta }}}_{i,j}\) and \({\varvec{\mathrm {\psi }}}_{j}\), she can pass Bob’s check (Eq. 12) for index i and all \(j\in [r]\) with probability at most \(1/2+\mathsf {negl}({s})\).
Consider that either Alice’s most-common OT input \(a\) is also her majority input, in which case we can pair each of the c OT instances where she has cheated with one where she is honest, or she has no majority input, in which case \(c\ge {s} + \lceil |m|/2\rceil \) and no more than \({s} + \lfloor |m|/2\rfloor \) of her cheats are identical. In the latter case, her identical cheats can be paired with honest OT instances an non-identically cheated OT instances. Thus, we can always find at least c pairs of indices i and \(i'\) such that \({\varvec{\mathrm {\Delta }}}_i\ne {\varvec{\mathrm {\Delta }}}_{i'}\), and such that all pairs are disjoint. Since we have supposed that \(c\ge {s} \), Alice’s probability of satisfying Eq. 12 over all combinations of indices is at most \((1/2+\mathsf {negl}({s}))^{s} \in \mathsf {negl}({s})\). Thus, in the ideal world,  always aborts, and in the real world, Bob aborts with probability overwhelming in \({s} \), and it follows that the real and ideal worlds are statistically indistinguishable in this case.
always aborts, and in the real world, Bob aborts with probability overwhelming in \({s} \), and it follows that the real and ideal worlds are statistically indistinguishable in this case.
Finally, we note that the above three cases partition the real-world conditions under which Eq. 12 does not hold. In other words, for every abort observed in the real world, an abort is also observed in the ideal world with negligibly different probability, and so the real and ideal worlds are statistically indistinguishable.
The Input Revelation phase of
 . In this phase of the protocol, the parties can open their inputs to one another. This phase may be run in place of the cheater check phase, but they may not both be run. It has no analogue in the protocols of Doerner et al. [19, 20]. For the sake of simplicity, we assume that both parties wish to reveal their inputs simultaneously, though the protocol may be extended to allow independent release. Alice begins the protocol with her input \(a\) and a check vector \(\tilde{{\varvec{\mathrm {a}}}}\), and output vectors \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) and \(\tilde{{\varvec{\mathrm {z}}}}_{{{\mathsf {A}}},*}\). Furthermore, she has an outstanding commitment to \((a,{\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*})\) from Step 6 of the multiplication phase. Bob begins with an input \(b\), a vector of choice bits \({\varvec{\mathrm {\beta }}}\) and an output vector \({\varvec{\mathrm {z}}}_{{{\mathsf {B}}}}\). In addition, they both know the vector \(\textsf {bit-sids}\) of session IDs of all relevant
. In this phase of the protocol, the parties can open their inputs to one another. This phase may be run in place of the cheater check phase, but they may not both be run. It has no analogue in the protocols of Doerner et al. [19, 20]. For the sake of simplicity, we assume that both parties wish to reveal their inputs simultaneously, though the protocol may be extended to allow independent release. Alice begins the protocol with her input \(a\) and a check vector \(\tilde{{\varvec{\mathrm {a}}}}\), and output vectors \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) and \(\tilde{{\varvec{\mathrm {z}}}}_{{{\mathsf {A}}},*}\). Furthermore, she has an outstanding commitment to \((a,{\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*})\) from Step 6 of the multiplication phase. Bob begins with an input \(b\), a vector of choice bits \({\varvec{\mathrm {\beta }}}\) and an output vector \({\varvec{\mathrm {z}}}_{{{\mathsf {B}}}}\). In addition, they both know the vector \(\textsf {bit-sids}\) of session IDs of all relevant  instances (i.e., one instance for each of Bob’s bits, where Alice was expected to use the same input in all instances), and they both know the uniformly sampled vector \({\varvec{\mathrm {g}}}\). The parties take the following steps:
instances (i.e., one instance for each of Bob’s bits, where Alice was expected to use the same input in all instances), and they both know the uniformly sampled vector \({\varvec{\mathrm {g}}}\). The parties take the following steps:
-
1.
For each \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\), Alice sends \((\texttt {transfer},\textsf {bit-sids}_i,j+1)\) to
 as a consequence, Bob receives \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}\) such that \(0\le {\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}<m\).
as a consequence, Bob receives \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}\) such that \(0\le {\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}<m\). -
2.
In order to prove that he used b as his input, Bob sends b and \(({\varvec{\mathrm {\beta }}}_i,{\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,*})\) for every \(i\in [|\textsf {bit-sids}|]\) to Alice, who verifies that
$$\begin{aligned} \delta \equiv \langle {\varvec{\mathrm {g}}},{\varvec{\mathrm {\beta }}}\rangle -b\pmod {m} \end{aligned}$$and that
$$\begin{aligned} {\tilde{\mathbf{z}}}_{{{\mathsf {A}}},i,j}+{\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j} \equiv {\varvec{\mathrm {\beta }}}_i\cdot \tilde{{\varvec{\mathrm {a}}}}_{j}\pmod {m} \end{aligned}$$for every \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\).
The security of this step lies in the inherent committing nature of OT; Bob is able to pass the test while also lying about his choice bit (without loss of generality, \({\varvec{\mathrm {\beta }}}_i\)) only by outright guessing the value for \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,*}\) that will cause the test to pass. This is as hard as guessing \(\tilde{{\varvec{\mathrm {a}}}}\), and Bob succeeds with probability less than \(2^{-{s}}\).
-
3.
In order to prove that she used an input a for all
 instances associated with the session IDs in \(\textsf {bit-sids}\), Alice decommits \((a,{\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*})\) via
instances associated with the session IDs in \(\textsf {bit-sids}\), Alice decommits \((a,{\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*})\) via 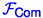 . Bob verifies that for each \(i\in [|\textsf {bit-sids}|]\), it holds that $$\begin{aligned} {\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i} + {\varvec{\mathrm {z}}}_{{{\mathsf {B}}},i} \equiv a\cdot {\varvec{\mathrm {\beta }}}_i \pmod {m} \end{aligned}$$
. Bob verifies that for each \(i\in [|\textsf {bit-sids}|]\), it holds that $$\begin{aligned} {\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i} + {\varvec{\mathrm {z}}}_{{{\mathsf {B}}},i} \equiv a\cdot {\varvec{\mathrm {\beta }}}_i \pmod {m} \end{aligned}$$Alice is able to subvert this check for some index i if and only if she correctly guesses Bob’s corresponding choice bit \({\varvec{\mathrm {\beta }}}_i\) during the input phase, and appropriately offsets \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i}\). Thus, her probability of success is negligible in the number of her cheats.
In the random oracle model, this protocol can be optimized by instructing Bob to send a \(2{s} \)-bit digest of his \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},*,*}\) values, instead of sending the values themselves, since Alice is able to recompute the same values herself using only \({\varvec{\mathrm {\beta }}}\) and the information already in her view. Under this optimization, the cost of this protocol is \(|m|+2{s} \) bits for Bob, \(|m|\cdot (|m|+2{s})\) bits for Alice, and 3 messages in total.
Simulating Input Revelation. Consider first a simulator against Bob. Recall that Bob has not thus far had an opportunity to cheat; each group of  instances commits him to an unambiguous input, which the simulator has previously extracted. The simulator sends a uniformly sampled vector \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},*,*}\) to Bob on behalf of
instances commits him to an unambiguous input, which the simulator has previously extracted. The simulator sends a uniformly sampled vector \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},*,*}\) to Bob on behalf of  , and aborts on behalf of Alice if any of the values it receives in Step 2 of the above protocol do not match the ones it has sent or extracted. On receiving Alice’s true input from
, and aborts on behalf of Alice if any of the values it receives in Step 2 of the above protocol do not match the ones it has sent or extracted. On receiving Alice’s true input from  , the simulator uses her input along with Bob’s extracted input and the values of \({\varvec{\mathrm {z}}}_{{{\mathsf {B}}},*}\) that it previously sent him to compute the correct value of \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) that it must send to Bob on behalf of
, the simulator uses her input along with Bob’s extracted input and the values of \({\varvec{\mathrm {z}}}_{{{\mathsf {B}}},*}\) that it previously sent him to compute the correct value of \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) that it must send to Bob on behalf of  . Under this simulation strategy, the ideal world is distinguishable from the real protocol to an adversary corrupting Bob only when Bob sends a combination of values in Step 2 that is incorrect (thus causing the simulator to abort) but nevertheless satisfies Alice’s check (avoiding an abort in the real world). The probability that he achieves this is negligible in the statistical parameter.
. Under this simulation strategy, the ideal world is distinguishable from the real protocol to an adversary corrupting Bob only when Bob sends a combination of values in Step 2 that is incorrect (thus causing the simulator to abort) but nevertheless satisfies Alice’s check (avoiding an abort in the real world). The probability that he achieves this is negligible in the statistical parameter.
Now consider simulation against Alice. Recall that if \(c\ge {s} \) (i.e., there were at least \({s} \) inconsistencies among Alice’s inputs to  in the input phase), then the simulator activated the \(\texttt {cheat}\) interface of
in the input phase), then the simulator activated the \(\texttt {cheat}\) interface of  and learned Bob’s input. If this happened, then we must prove that the real-world Bob always aborts during Input Revelation. If \(c<{s} \), then the simulator sampled a set of c simulated choice bits \(\hat{{\varvec{\mathrm {\beta }}}}\) (one bit for each location where Alice cheated) and used them to calculate Alice’s output in the multiplication phase. It is possible that the environment was able to learn those bits, and thus, we must prove that they are compatible with whatever input the simulator is required to reveal.
and learned Bob’s input. If this happened, then we must prove that the real-world Bob always aborts during Input Revelation. If \(c<{s} \), then the simulator sampled a set of c simulated choice bits \(\hat{{\varvec{\mathrm {\beta }}}}\) (one bit for each location where Alice cheated) and used them to calculate Alice’s output in the multiplication phase. It is possible that the environment was able to learn those bits, and thus, we must prove that they are compatible with whatever input the simulator is required to reveal.
As before, let \({\varvec{\mathrm {\alpha }}}\) and \(\tilde{{\varvec{\mathrm {\alpha }}}}\in {\mathbb {Z}}_m^{|{\varvec{\mathrm {\alpha }}}|\times r}\) represent Alice’s her actual inputs to the OTs, where \(|{\varvec{\mathrm {\alpha }}}|=|\textsf {bit-sids}|\) and where \({{\varvec{\mathrm {\alpha }}}}_{i} = {{\varvec{\mathrm {\alpha }}}}_{i'} = a\) and \(\tilde{{\varvec{\mathrm {\alpha }}}}_{i,*} = \tilde{{\varvec{\mathrm {\alpha }}}}_{i',*} = {{\tilde{\mathbf{a}}}}\) for all \(i,i'\in [|{\varvec{\mathrm {\alpha }}}|]\) if Alice was honest. Additionally, let \((a',{\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*})\) be the values to which Alice actually committed in Step 6 of the multiplication phase, where \(a'=a\) and \({\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*}={\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) if Alice was honest.
Let us first consider the case that \(c<{s} \). In this case, the simulator begins by sending an \(\texttt {open}\) message with the correct session ID to  , and in return it receives Bob’s input \(b\). In order to simulate Step 2 of the protocol, the simulator must sample a set of choice bits \({\varvec{\mathrm {\beta }}}\) such that
, and in return it receives Bob’s input \(b\). In order to simulate Step 2 of the protocol, the simulator must sample a set of choice bits \({\varvec{\mathrm {\beta }}}\) such that
for \(\delta \) and \(b\) and \({\varvec{\mathrm {g}}}\) that have previously been fixed. We can simplify the problem by rewriting it as follows: let \(b':=b+\delta -\langle {\varvec{\mathrm {g}}}, \hat{{\varvec{\mathrm {\beta }}}}\rangle \bmod {m}\) (recall that \(\hat{{\varvec{\mathrm {\beta }}}}_i=0\iff i\not \in {\varvec{\mathrm {I}}}\)), and let \(\smash {{\varvec{\mathrm {g}}}'\in {\mathbb {Z}}_m^{|{\varvec{\mathrm {g}}}|-c}}\) be the result of deleting from \({\varvec{\mathrm {g}}}\) each \({\varvec{\mathrm {g}}}_i\) with index \(i\in {\varvec{\mathrm {I}}}\). The simulator can clearly find \({\varvec{\mathrm {\beta }}}\) satisfying Eq. 13 if it can find \({\varvec{\mathrm {\beta }}}'\in \{0,1\}^{|{\varvec{\mathrm {g}}}|-c}\) such that \(\langle {\varvec{\mathrm {g}}}',{\varvec{\mathrm {\beta }}}'\rangle \equiv b'\pmod {m}\). We encapsulate the proof that the simulator can find such a \({\varvec{\mathrm {\beta }}}'\) efficiently into the following lemma:
Lemma B.4
There exists an algorithm \(\mathsf {Brute}\) such that for \(c\le {s} \) and any arbitrary \(b'\in [0, m)\),
where the probability is taken over the distribution of \({\varvec{\mathrm {g}}}'\) and the internal coins of \(\mathsf {Brute}\). If \(m\in O({s})\), then the running time of \(\mathsf {Brute}\) is in \(O({s} ^2)\).
Proof
The algorithm \(\mathsf {Brute}\) works by repeatedly guessing uniform values of \({\varvec{\mathrm {\beta }}}'\) until the predicate \(\smash {\langle {\varvec{\mathrm {g}}}',{\varvec{\mathrm {\beta }}}' \rangle \equiv b'\pmod {m}}\) is satisfied. Given a particular value of c, it follows from Impagliazzo and Naor [31, Proposition 1.1.2] that a single uniformly random assignment of \({\varvec{\mathrm {\beta }}}'\) satisfies the predicate with probability no less than
and since we have assumed that \(c\le {s} \), we have:
Thus, in order to find a satisfying assignment of \({\varvec{\mathrm {\beta }}}'\) with probability overwhelming in \({s} \), \(\mathsf {Brute}\) must make g guesses such that
Taking the natural log of both sides of this equation and using the fact that \(\ln (1+x)\ge x/(1+x)\) if \(x > -1\), we have
and it follows that if \(m\in O({s})\), then there is a sufficiently large value of g in \(O({s} ^2)\), and this determines the runtime of \(\mathsf {Brute}\). \(\square \)
Having found an appropriate set of choice bits \({\varvec{\mathrm {\beta }}}\) by brute force, the simulator sends it to Alice, along with the exact value of \(\tilde{{\varvec{\mathrm {z}}}}_{{{\mathsf {B}}},*,*}\) that will cause her check to pass (which the simulator can calculate, since it knows all other values used in her check), and thereby Step 2 of the protocol is simulated. To simulate Step 3 of the protocol, the simulator can simply evaluate Bob’s check exactly as he would, and then instruct  to abort if Bob’s check would fail. In the case that \(c<{s} \), the real and ideal world experiments are statistically indistinguishable.
to abort if Bob’s check would fail. In the case that \(c<{s} \), the real and ideal world experiments are statistically indistinguishable.
Now let us consider the case that \(c\ge {s} \). In this case, the simulator already knows Bob’s inputs, and thus, it can simulate his behavior exactly. Since  is doomed to abort in this case, we must prove that Bob aborts with overwhelming probability in the real world as well. Recall that \(|{\varvec{\mathrm {I}}}| = c\) and that \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i}+{\varvec{\mathrm {z}}}_{{{\mathsf {B}}},i} \equiv {\varvec{\mathrm {\beta }}}_i\cdot (a+{\varvec{\mathrm {\Delta }}}_i)\pmod {m}\) and that \({\varvec{\mathrm {\Delta }}}_i\ne 0\iff i\in {\varvec{\mathrm {I}}}\) and that \({\varvec{\mathrm {\beta }}}\) was uniformly sampled and information-theoretically hidden from Alice when she committed to \((a',{\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*})\). Given the value \(a'\) that she chooses, Alice must commit
is doomed to abort in this case, we must prove that Bob aborts with overwhelming probability in the real world as well. Recall that \(|{\varvec{\mathrm {I}}}| = c\) and that \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i}+{\varvec{\mathrm {z}}}_{{{\mathsf {B}}},i} \equiv {\varvec{\mathrm {\beta }}}_i\cdot (a+{\varvec{\mathrm {\Delta }}}_i)\pmod {m}\) and that \({\varvec{\mathrm {\Delta }}}_i\ne 0\iff i\in {\varvec{\mathrm {I}}}\) and that \({\varvec{\mathrm {\beta }}}\) was uniformly sampled and information-theoretically hidden from Alice when she committed to \((a',{\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*})\). Given the value \(a'\) that she chooses, Alice must commit
in order to pass Bob’s check at some index i. If \(a'-a-{\varvec{\mathrm {\Delta }}}_i\not \equiv 0\pmod {m}\), then she will have committed the correct value with probability at most 1/2. When \(c\ge {s} \), it must hold that \(a'-a-{\varvec{\mathrm {\Delta }}}_i\not \equiv 0\pmod {m}\) for at least c indices i (notice that setting \(a' \ne a\) can only hurt Alice), and she avoids an abort in the real world with probability no more than \(2^{-c}\le 2^{-{s}}\). Thus, the real world is statistically indistinguishable from the ideal world, when \(c\ge {s} \).
1.3 B.3. Multiparty Reusable-Input Multiplier
Plugging  into a GMW-style multiplication protocol [26] yields an n-party equivalent of the same functionality, i.e.,
into a GMW-style multiplication protocol [26] yields an n-party equivalent of the same functionality, i.e.,  . This flavor of composition is standard (it is used, for example, by Doerner et al. [20]), and the security argument follows along similar lines to prior work. Note that we give the ideal adversary slightly more power than strictly necessary, in order to simplify our description: when it cheats, it always learns the secret inputs of all honest parties; in the real protocol, on the other hand, the adversary may cheat on honest parties individually.
. This flavor of composition is standard (it is used, for example, by Doerner et al. [20]), and the security argument follows along similar lines to prior work. Note that we give the ideal adversary slightly more power than strictly necessary, in order to simplify our description: when it cheats, it always learns the secret inputs of all honest parties; in the real protocol, on the other hand, the adversary may cheat on honest parties individually.

We defer an efficiency analysis of the protocol that realizes this functionality to the next subsection.
1.4 B.4. Augmented Multiplication
Finally, we describe a protocol  that realizes
that realizes  in the
in the  ,
, -hybrid model. It comprises five phases. Its input, multiplication, and input revelation phases essentially fall through to
-hybrid model. It comprises five phases. Its input, multiplication, and input revelation phases essentially fall through to  . Its cheater check phase falls through to the cheater check phase of
. Its cheater check phase falls through to the cheater check phase of  , but also takes additional steps to securely evaluate an arbitrary predicate over the checked values, using generic MPC. Finally, it adds a sampling phase, which samples pairs of nonzero values by running a sequence of
, but also takes additional steps to securely evaluate an arbitrary predicate over the checked values, using generic MPC. Finally, it adds a sampling phase, which samples pairs of nonzero values by running a sequence of  instructions.
instructions.
Theorem B.6
The protocol  statistically UC-realizes
statistically UC-realizes  in the
in the  ,
,  -hybrid model against a malicious adversary that statically corrupts \(n-1\) parties.
-hybrid model against a malicious adversary that statically corrupts \(n-1\) parties.




We now discuss security and efficiency of  , phase-by-phase.
, phase-by-phase.
Input. The input phase of  defers directly to
defers directly to  , and therefore inherits its security. When realized as we have discussed in Sect. B.3, a single call to
, and therefore inherits its security. When realized as we have discussed in Sect. B.3, a single call to  among all parties corresponds to all pairs of parties making two calls each to
among all parties corresponds to all pairs of parties making two calls each to  . Recall that in
. Recall that in  , loading inputs from the party playing Bob is effectively free, and as a consequence, we need only count costs due to inputs loaded from Alice. The first party, \(\mathcal{P} _1\), plays Alice in all of its interactions with
, loading inputs from the party playing Bob is effectively free, and as a consequence, we need only count costs due to inputs loaded from Alice. The first party, \(\mathcal{P} _1\), plays Alice in all of its interactions with  , and pays a cost of \((n-1)\cdot (|m|\cdot (|m|+2{s})+4{\lambda })\) bits if
, and pays a cost of \((n-1)\cdot (|m|\cdot (|m|+2{s})+4{\lambda })\) bits if  is realized via Silent OT [6] or KOS OT [35]. The last party, \(\mathcal{P} _n\), always plays Bob, and pays a cost of \((n-1)\cdot (2|m|+2{s})\) bits if
is realized via Silent OT [6] or KOS OT [35]. The last party, \(\mathcal{P} _n\), always plays Bob, and pays a cost of \((n-1)\cdot (2|m|+2{s})\) bits if  is realized via Silent OT, or \((n-1)\cdot ({\lambda } \cdot (|m|+2{s})+|m|)\) bits if
is realized via Silent OT, or \((n-1)\cdot ({\lambda } \cdot (|m|+2{s})+|m|)\) bits if  is realized via KOS OT. The other parties play a mixture of the roles, and thus in general they each pay an average costFootnote 17 of
is realized via KOS OT. The other parties play a mixture of the roles, and thus in general they each pay an average costFootnote 17 of

transmitted bits with Silent OT or

transmitted bits with KOS OT. Regardless, three rounds are required.
Multiplication. The input phase of  defers directly to
defers directly to  . As we have noted in Sect. B.2, the multiplication and input phases of
. As we have noted in Sect. B.2, the multiplication and input phases of  cost the same; however, whereas the input phase of
cost the same; however, whereas the input phase of  corresponds costwise to one invocation of the input phase of
corresponds costwise to one invocation of the input phase of  for each pair of parties (due to Bob’s inputs being free), the multiplication phase of
for each pair of parties (due to Bob’s inputs being free), the multiplication phase of  corresponds to two invocations of the multiplication phase of
corresponds to two invocations of the multiplication phase of  for each pair of parties. Thus, the parties pay three rounds and an average cost of
for each pair of parties. Thus, the parties pay three rounds and an average cost of  transmitted bits per party. Note that as an optimization two input phases can be fused with one multiplication (in which they are used), and the inputs will consequently add no additional cost.
transmitted bits per party. Note that as an optimization two input phases can be fused with one multiplication (in which they are used), and the inputs will consequently add no additional cost.
Input revelation. The input revelation phase of  defers directly to
defers directly to  , and corresponds to two invocations of the
, and corresponds to two invocations of the  open command for each pair of parties (where each invocation opens both parties’ inputs). Thus, the cost of this phase is
open command for each pair of parties (where each invocation opens both parties’ inputs). Thus, the cost of this phase is

transmitted bits per party on average, and three rounds.
Sampling. This procedure is probabilistic. Specifically, each iteration succeeds with probability \(((m-1)/m)^3\). We will analyze the costs associated with iterating sequentially until a value is successfully sampled (as described in  ). So long as only a single instance of the sampling procedure is considered, the expected number of sequential iterations depends only on \(m\), but we note that when multiple instances of the sampling procedure are run concurrently, the expected maximum number of iterations among the concurrent instances grows with the number of instances [14]. Such concurrency is required in order to achieve biprime sampling in expected-constant or constant rounds, as discussed in Sect. 6.4. In order to avoid huge overhead costs, an elaborate analysis is required. We perform this analysis in Sect. 6.4 and, as we have said, focus here on the sequential case.
). So long as only a single instance of the sampling procedure is considered, the expected number of sequential iterations depends only on \(m\), but we note that when multiple instances of the sampling procedure are run concurrently, the expected maximum number of iterations among the concurrent instances grows with the number of instances [14]. Such concurrency is required in order to achieve biprime sampling in expected-constant or constant rounds, as discussed in Sect. 6.4. In order to avoid huge overhead costs, an elaborate analysis is required. We perform this analysis in Sect. 6.4 and, as we have said, focus here on the sequential case.
In the sequential case, \((m/(m-1))^3\) iterations are required in expectation. Each iteration requires two calls to the  multiplication command (we will assume that the
multiplication command (we will assume that the  input command is coalesced and therefore free, as described previously), and all iterations after the first require two invocations of the
input command is coalesced and therefore free, as described previously), and all iterations after the first require two invocations of the  open command. In addition, every party broadcasts a value in \({\mathbb {Z}}_m\) to the other parties in each iteration. Thus, the average cost per party is
open command. In addition, every party broadcasts a value in \({\mathbb {Z}}_m\) to the other parties in each iteration. Thus, the average cost per party is

transmitted bits, in expectation, and the expected round count is \(10(m/(m-1))^3 -3\). For values of \(m\) of any significant size, these costs converge to the cost of two sequential multiplications, plus one additional round.
With respect to security, we observe that the values \({\tilde{z}}_i\) for \(i\in [n]\) jointly reveal nothing about the secret values \(x_i\) and \(y_i\), because the latter pair of values have been masked by \(r_i\). Thus, the security of a successful iteration reduces directly to the security of the constituent multipliers.Footnote 18 In failed iterations, all values are opened and the computations are checked locally by each party. This ensures that the adversary cannot force sampling failures by cheating, and thereby prevent the protocol from terminating.
Predicate cheater check. Unlike the other protocol phases, this phase takes an input of flexible dimension and therefore its cost does not have a convenient closed-form cost. Consequently, we will describe the cost piecemeal. For each input to be checked, let \(m\) be the modulus with which the input is associated and let c be the number of multiplications in which it has been used. The parties engage in \(\lceil {s}/|m|\rceil \) additional invocations of the  Multiplication command, with inputs that have previously been loaded, and then run the Cheater Check command of
Multiplication command, with inputs that have previously been loaded, and then run the Cheater Check command of  , which implies running the Cheater Check command of
, which implies running the Cheater Check command of  in a pairwise fashion. Together, these operations incur a cost of
in a pairwise fashion. Together, these operations incur a cost of

transmitted bits per party, on average. Finally, for every input to be checked, the parties each input \(\lceil {s}/|m| + 1\rceil \cdot |m|\) bits into a generic MPC, and then run a circuit that performs \(3\cdot (n-1)\cdot \lceil {s}/|m|\rceil \) modular additions and \(\lceil {s}/|m|\rceil \) modular multiplications and equality tests over \({\mathbb {Z}}_m\). Using the circuit component sizes reported in Sect. 6.2, the size of this circuit comprises \((3\cdot (n-1)\cdot \mathsf {modadd}(|m|)+\mathsf {modmul}(|m|) + |m| )\cdot \lceil {s}/|m|\rceil \) AND gates, with \(|m|\) additional gates in the case that the input to be checked was sampled. In addition to these costs for each input to be checked, the generic MPC also evaluates the predicate f, comprising |f| AND gates, over the inputs already loaded. A handful of additional AND gates are required to combine the results from the predicate and the per-input checks, and the circuit has exactly one output wire.
With respect to security, we note that the protocol effectively uses a straightforward composition of secure parts to implement an information-theoretic MAC over the shared values corresponding to the inputs to be checked, in order to ensure that they are transferred into the circuit of the generic MPC faithfully. Forced reuse ensures that the MACs are applied to the correct values, and because each MAC has soundness error \(1/m=2^{-|m|}\), it is necessary to repeat the process \({s}/|m|\) times in order to achieve a soundness error of \(2^{-{s}}\). The multiplications (including those used to apply the MACs) are then checked for cheats, and the MACs are verified inside the circuit before the predicate f is evaluated.
Appendix C. Proof of Security for Our Biprime-Sampling Protocol
In this section, we provide the full proof of Theorem 4.6, showing that  realizes
realizes  in the malicious setting.
in the malicious setting.
Theorem 4.6
If factoring biprimes sampled by  is hard, then
is hard, then  UC-realizes
UC-realizes  in the
in the  -hybrid model against a malicious PPT adversary that statically corrupts up to \(n-1\) parties.
-hybrid model against a malicious PPT adversary that statically corrupts up to \(n-1\) parties.
Proof
We begin by describing a simulator  for the adversary \(\mathcal A\). Next, we prove by a sequence of hybrid experiments that no PPT environment can distinguish with more than negligible probability between running with the dummy adversary and real parties executing
for the adversary \(\mathcal A\). Next, we prove by a sequence of hybrid experiments that no PPT environment can distinguish with more than negligible probability between running with the dummy adversary and real parties executing  , and running with
, and running with  and dummy parties that interact with
and dummy parties that interact with  . Formally speaking, we show that
. Formally speaking, we show that

for all environments \(\mathcal{Z} \), assuming the hardness of factoring primes generated by  . Since the following simulator is quite long and involves complex state tracking, we invite the reader to revisit Sect. 4.4 for an overview of the simulation strategy.
. Since the following simulator is quite long and involves complex state tracking, we invite the reader to revisit Sect. 4.4 for an overview of the simulation strategy.







We now define our sequence of hybrid experiments. The output of each experiment is the output of the environment, \(\mathcal{Z} \). We begin with the real-world experiment, constructed per the standard formulation for UC-security.

Hybrid \(\mathcal {H}_{1}\). In this experiment, we replace the real honest parties with dummy parties. We then construct a simulator that plays the role of  in its interactions with the dummy parties, and also plays the roles of the honest parties in their interactions with the corrupt parties. Furthermore, the simulator plays the roles of
in its interactions with the dummy parties, and also plays the roles of the honest parties in their interactions with the corrupt parties. Furthermore, the simulator plays the roles of  and
and  in their interactions with the corrupt parties and with the adversary \(\mathcal A\). Internally, the simulator emulates each honest party by running its code, and it emulates
in their interactions with the corrupt parties and with the adversary \(\mathcal A\). Internally, the simulator emulates each honest party by running its code, and it emulates  and
and  similarly. By observing the output of each emulated honest party, the simulator can send the appropriate message to each dummy party on behalf of
similarly. By observing the output of each emulated honest party, the simulator can send the appropriate message to each dummy party on behalf of  , such that the outcome of the experiment for each dummy party matches the output for the corresponding honest party. The distribution of \(\mathcal {H}_{1}\) is thus clearly identical to that of \(\mathcal {H}_{0}\).
, such that the outcome of the experiment for each dummy party matches the output for the corresponding honest party. The distribution of \(\mathcal {H}_{1}\) is thus clearly identical to that of \(\mathcal {H}_{0}\).
Hybrid \(\mathcal {H}_{2}\). This hybrid experiment is identical to \(\mathcal {H}_{1}\), except that in \(\mathcal {H}_{2}\), the simulator does not internally emulate the honest parties for Steps 1 through 3 of  . Instead, the simulator takes one of the following two branches:
. Instead, the simulator takes one of the following two branches:
-
If \(\mathcal A\) sends a \(\texttt {cheat}\) message to
 before Step 4 of
before Step 4 of  , or if there is any \(i\in {{\varvec{\mathrm {P}}}^*} \) and \(j'\in [\ell +1,{\ell '}]\) such that
, or if there is any \(i\in {{\varvec{\mathrm {P}}}^*} \) and \(j'\in [\ell +1,{\ell '}]\) such that 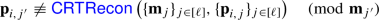
then at the time the cheat occurs, the simulator must retroactively construct views for the honest parties that are consistent with the outputs already delivered to the corrupt parties.Footnote 19 After this, the simulation is completed using the same strategy as in \(\mathcal {H}_{1}\) (i.e., the honest parties are internally emulated by the simulator). It follows immediately from the perfect security of additive secret sharing that \(\mathcal {H}_{2}\) and \(\mathcal {H}_{1}\) are identically distributed in this branch.
-
If \(\mathcal A\) does not send a \(\texttt {cheat}\) message to
 before Step 4 of
before Step 4 of  , and if for all \(i\in {{\varvec{\mathrm {P}}}^*} \) and \(j'\in [\ell +1,{\ell '}]\) it holds that
, and if for all \(i\in {{\varvec{\mathrm {P}}}^*} \) and \(j'\in [\ell +1,{\ell '}]\) it holds that 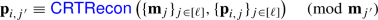
then before simulating Step 4, the simulator uses the corrupt parties’ inputs (which it received in its role as
 ) to compute
) to compute 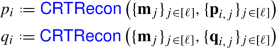
for \(i\in {{\varvec{\mathrm {P}}}^*} \). Next, the simulator runs
 internally, receives as output either \((\texttt {success}, p, q)\) or \((\texttt {failure}, p, q)\), and computes \(N:=p\cdot q\). With these values, the simulator retroactively constructs views for the honest parties by sampling \(({\varvec{\mathrm {p}}}_{i,j},{\varvec{\mathrm {q}}}_{i,j},{\varvec{\mathrm {N}}}_{i,j})\leftarrow {\mathbb {Z}}^3_{{\varvec{\mathrm {m}}} _j}\) uniformly for
internally, receives as output either \((\texttt {success}, p, q)\) or \((\texttt {failure}, p, q)\), and computes \(N:=p\cdot q\). With these values, the simulator retroactively constructs views for the honest parties by sampling \(({\varvec{\mathrm {p}}}_{i,j},{\varvec{\mathrm {q}}}_{i,j},{\varvec{\mathrm {N}}}_{i,j})\leftarrow {\mathbb {Z}}^3_{{\varvec{\mathrm {m}}} _j}\) uniformly for  and \(j\in [{\ell '}]\) subject to $$\begin{aligned} \sum _{i\in [n]} {\varvec{\mathrm {p}}}_{i,j}\equiv p\pmod {{\varvec{\mathrm {m}}} _j}&\qquad \text { and}\qquad \sum _{i\in [n]} {\varvec{\mathrm {q}}}_{i,j}\equiv q\pmod {{\varvec{\mathrm {m}}} _j} \\ \text {and}\qquad&\sum _{i\in [n]} {\varvec{\mathrm {N}}}_{i,j}\equiv N\pmod {{\varvec{\mathrm {m}}} _j} \end{aligned}$$
and \(j\in [{\ell '}]\) subject to $$\begin{aligned} \sum _{i\in [n]} {\varvec{\mathrm {p}}}_{i,j}\equiv p\pmod {{\varvec{\mathrm {m}}} _j}&\qquad \text { and}\qquad \sum _{i\in [n]} {\varvec{\mathrm {q}}}_{i,j}\equiv q\pmod {{\varvec{\mathrm {m}}} _j} \\ \text {and}\qquad&\sum _{i\in [n]} {\varvec{\mathrm {N}}}_{i,j}\equiv N\pmod {{\varvec{\mathrm {m}}} _j} \end{aligned}$$and then the simulator completes the simulation using the same strategy as in \(\mathcal {H}_{1}\) (i.e., it emulates the honest parties internally).
Recall that by construction
 samples from a distribution identical to that of
samples from a distribution identical to that of  , conditioned on honest behavior during the Candidate Sieving phase of the protocol. Consequently, it follows from the perfect security of additive secret sharing that \(\mathcal {H}_{2}\) and \(\mathcal {H}_{1}\) are identically distributed if this branch is taken. Note furthermore that in \(\mathcal {H}_{2}\) the output of
, conditioned on honest behavior during the Candidate Sieving phase of the protocol. Consequently, it follows from the perfect security of additive secret sharing that \(\mathcal {H}_{2}\) and \(\mathcal {H}_{1}\) are identically distributed if this branch is taken. Note furthermore that in \(\mathcal {H}_{2}\) the output of  will be \(\texttt {biprime}\) only if
will be \(\texttt {biprime}\) only if
 returns \(\texttt {success}\) or if there exists some \(i\in {{\varvec{\mathrm {P}}}^*} \) such that \(p_i\ne p'_i\) or \(q_i\ne q'_i\), where \(p'_i\) and \(q'_i\) are corrupt inputs to
returns \(\texttt {success}\) or if there exists some \(i\in {{\varvec{\mathrm {P}}}^*} \) such that \(p_i\ne p'_i\) or \(q_i\ne q'_i\), where \(p'_i\) and \(q'_i\) are corrupt inputs to  .
.
Hybrid \(\mathcal {H}_{3}\). This hybrid experiment is identical to \(\mathcal {H}_{2}\), except in the way that  is simulated in Step 6 of
is simulated in Step 6 of  . Recall that in \(\mathcal {H}_{2}\), the simulator runs the code of
. Recall that in \(\mathcal {H}_{2}\), the simulator runs the code of  internally, and in order to do this, it must know the factorization of the candidate biprime \(N\) in all cases. In \(\mathcal {H}_{3}\), if no cheating occurs until after the biprimality test, and the candidate is in fact a biprime, then the simulator does not use the factorization of the candidate biprime to simulate
internally, and in order to do this, it must know the factorization of the candidate biprime \(N\) in all cases. In \(\mathcal {H}_{3}\), if no cheating occurs until after the biprimality test, and the candidate is in fact a biprime, then the simulator does not use the factorization of the candidate biprime to simulate  .
.
If cheating occurs before Step 4 of  is simulated, then \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) are identical: the simulator simply emulates the honest parties internally (retroactively sampling their views as previously described). The experiments differ, however, if no cheating occurs before Step 4 of
is simulated, then \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) are identical: the simulator simply emulates the honest parties internally (retroactively sampling their views as previously described). The experiments differ, however, if no cheating occurs before Step 4 of  . Recall that in \(\mathcal {H}_{2}\), under this condition, the simulator runs
. Recall that in \(\mathcal {H}_{2}\), under this condition, the simulator runs  internally and receives \(p\) and \(q\) (plus an indication as to whether they are both primes), from which values it constructs honest-party views that are subsequently used to simulate
internally and receives \(p\) and \(q\) (plus an indication as to whether they are both primes), from which values it constructs honest-party views that are subsequently used to simulate  . In \(\mathcal {H}_{3}\), if no cheating occurs before Step 4 of
. In \(\mathcal {H}_{3}\), if no cheating occurs before Step 4 of  , then there are four cases. Let \(N'\) be the candidate biprime reconstructed in Step 4 of
, then there are four cases. Let \(N'\) be the candidate biprime reconstructed in Step 4 of  , which may not equal \(N\) if cheating occurs, and let \((\texttt {check-biprimality},\mathsf {sid},N^{\prime \prime }_i,p'_i,q'_i)\) be the message received on behalf of
, which may not equal \(N\) if cheating occurs, and let \((\texttt {check-biprimality},\mathsf {sid},N^{\prime \prime }_i,p'_i,q'_i)\) be the message received on behalf of  from \(\mathcal{P} _i\) for every \(i\in {{\varvec{\mathrm {P}}}^*} \) in Step 6 of
from \(\mathcal{P} _i\) for every \(i\in {{\varvec{\mathrm {P}}}^*} \) in Step 6 of  . The four cases are as follows.
. The four cases are as follows.
-
1.
If
 reports that \(N\) is a biprime, and the adversary continues to behave honestly (i.e., in Steps 4 and 6 of
reports that \(N\) is a biprime, and the adversary continues to behave honestly (i.e., in Steps 4 and 6 of  , the corrupt parties transmit values that add up to the expected sums), then the simulator outputs \(\texttt {biprime}\) to \(\mathcal A\) on behalf of
, the corrupt parties transmit values that add up to the expected sums), then the simulator outputs \(\texttt {biprime}\) to \(\mathcal A\) on behalf of  , and reports the same outcome to the corrupt parties if it receives \(\texttt {proceed}\) from \(\mathcal A\) in reply. Note that knowledge of \(p\) and \(q\) is not used in this eventuality. If \(\mathcal A\) instead replies to
, and reports the same outcome to the corrupt parties if it receives \(\texttt {proceed}\) from \(\mathcal A\) in reply. Note that knowledge of \(p\) and \(q\) is not used in this eventuality. If \(\mathcal A\) instead replies to  with \(\texttt {cheat}\), then \(p\) and \(q\) are used to formulate the correct response.
with \(\texttt {cheat}\), then \(p\) and \(q\) are used to formulate the correct response. -
2.
If the previous case does not occur, and
 reports that \(N\) is a biprime, but there exists some \(i\in {{\varvec{\mathrm {P}}}^*} \) such that \(N^{\prime \prime }_i\ne N'\), then the simulator sends \(\texttt {non-biprime}\) to the corrupt parties on behalf of
reports that \(N\) is a biprime, but there exists some \(i\in {{\varvec{\mathrm {P}}}^*} \) such that \(N^{\prime \prime }_i\ne N'\), then the simulator sends \(\texttt {non-biprime}\) to the corrupt parties on behalf of  .
. -
3.
If neither of previous cases occurs, and
 reports that \(N\) is a biprime, and \(N^{\prime \prime }_i=N\) for all \(i\in {{\varvec{\mathrm {P}}}^*} \), but $$\begin{aligned} \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}p'_i\ne \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}p_i \qquad \text { or}\qquad \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}q'_i\ne \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}q_i\end{aligned}$$
reports that \(N\) is a biprime, and \(N^{\prime \prime }_i=N\) for all \(i\in {{\varvec{\mathrm {P}}}^*} \), but $$\begin{aligned} \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}p'_i\ne \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}p_i \qquad \text { or}\qquad \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}q'_i\ne \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}q_i\end{aligned}$$then the simulator sends \(\texttt {non-biprime}\) to the corrupt parties on behalf of
 .
. -
4.
If none of the previous cases occur, and
 reports that \(N\) is not a biprime, or for all \(i\in {{\varvec{\mathrm {P}}}^*} \) it holds that \(N^{\prime \prime }_i=N'\ne N\), then the simulator constructs honest-party views from \(p\) and \(q\) and runs the code of
reports that \(N\) is not a biprime, or for all \(i\in {{\varvec{\mathrm {P}}}^*} \) it holds that \(N^{\prime \prime }_i=N'\ne N\), then the simulator constructs honest-party views from \(p\) and \(q\) and runs the code of  , as in \(\mathcal {H}_{2}\).
, as in \(\mathcal {H}_{2}\).
It is easy to see that \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) are identically distributed in first, second, and fourth cases above, and also in the case that cheating occurs before Step 4 of  . It remains only to analyze the third case. In \(\mathcal {H}_{3}\), it leads to an unconditional abort,Footnote 20 whereas in \(\mathcal {H}_{2}\), the adversary can avoid an abort by sending \(p'_i\) and \(q'_i\) for \(i\in {{\varvec{\mathrm {P}}}^*} \) such that
. It remains only to analyze the third case. In \(\mathcal {H}_{3}\), it leads to an unconditional abort,Footnote 20 whereas in \(\mathcal {H}_{2}\), the adversary can avoid an abort by sending \(p'_i\) and \(q'_i\) for \(i\in {{\varvec{\mathrm {P}}}^*} \) such that
which can be achieved without falling into the first case by finding values of \(p'_i\) and \(q'_i\) such that the factors supplied to  are effectively switched relative to their honest order. This is the only condition under which \(\mathcal {H}_{3}\) differs observably from \(\mathcal {H}_{2}\), and thus the environment’s advantage in distinguishing the two hybrids is determined exclusively by the probability that the adversary triggers this condition. We wish to show that the two hybrids are computationally indistinguishable under the assumption that biprimes drawn from the distribution of
are effectively switched relative to their honest order. This is the only condition under which \(\mathcal {H}_{3}\) differs observably from \(\mathcal {H}_{2}\), and thus the environment’s advantage in distinguishing the two hybrids is determined exclusively by the probability that the adversary triggers this condition. We wish to show that the two hybrids are computationally indistinguishable under the assumption that biprimes drawn from the distribution of  are hard to factor. We begin by giving a simpler description of the adversary’s task in the form of a game that is won by the adversary if the following experiment outputs 1.
are hard to factor. We begin by giving a simpler description of the adversary’s task in the form of a game that is won by the adversary if the following experiment outputs 1.

Note that a reduction from winning the  game to distinguishing between \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) exists by construction and there is no loss of advantage. Now consider a variation on the classic factoring game (see Experiment 3.1) in which
game to distinguishing between \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) exists by construction and there is no loss of advantage. Now consider a variation on the classic factoring game (see Experiment 3.1) in which  is used in place of \(\mathsf {GenModulus}\), and the adversary supplies a set of corrupt shares to
is used in place of \(\mathsf {GenModulus}\), and the adversary supplies a set of corrupt shares to  .
.

We will show a lossless reduction from winning the  game to winning the
game to winning the  game, which implies as a corollary that any adversary enabling the environment to distinguish \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) can be used to factor biprimes produced by
game, which implies as a corollary that any adversary enabling the environment to distinguish \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) can be used to factor biprimes produced by  with adversarial shares.
with adversarial shares.
Lemma C.4
For every PPT adversary \(\mathcal{A} \), there exists a PPT adversary \(\mathcal{B} \) such that for all \({\kappa },n\in {\mathbb {N}}\) and \({{\varvec{\mathrm {P}}}^*} \subset [n]\), it holds that

Proof
Our reduction plays the role of \(\mathcal{B} \) in Experiment C.3, and the role of the challenger in Experiment C.2. It works as follows.
-
1.
When invoked as \(\mathcal{B} \) with inputs \({\kappa } \) and \({{\varvec{\mathrm {P}}}^*} \) in Experiment C.3, invoke \(\mathcal{A} (1^{\kappa },{{\varvec{\mathrm {P}}}^*})\) in Experiment C.2. On receiving \(p_i\) and \(q_i\) for \(i\in {{\varvec{\mathrm {P}}}^*} \) from \(\mathcal{A} \), forward them to the challenger in Experiment C.3.
-
2.
On receiving \(N\) as \(\mathcal{B} \) in Experiment C.3, forward it to \(\mathcal{A} \) in Experiment C.2. Receive \(p'_i\) and \(q'_i\) for \(i\in {{\varvec{\mathrm {P}}}^*} \)
-
3.
Try to solve the following system of equations for unknowns \(p_\mathcal{H} \) and \(q_\mathcal{H} \)
$$\begin{aligned} \left( p_\mathcal{H} +\sum _{i\in {{\varvec{\mathrm {P}}}^*}}p_i\right) \cdot \left( q_\mathcal{H} + \sum _{i\in {{\varvec{\mathrm {P}}}^*}}q_i\right) = \left( p_\mathcal{H} +\sum _{i\in {{\varvec{\mathrm {P}}}^*}}p'_i\right) \cdot \left( q_\mathcal{H} + \sum _{i\in {{\varvec{\mathrm {P}}}^*}}q'_i\right) = N\end{aligned}$$and if exactly one valid pair \((p_\mathcal{H},q_\mathcal{H})\) exists, then send
$$\begin{aligned} p':=p_\mathcal{H} +\sum _{i\in {{\varvec{\mathrm {P}}}^*}}p'_i\qquad \text { and}\qquad q':=q_\mathcal{H} +\sum _{i\in {{\varvec{\mathrm {P}}}^*}}q'_i \end{aligned}$$to the challenger in Experiment C.3. Otherwise, send \(\bot \) to the challenger.
This reduction is correct and lossless by construction. \(\mathcal{A} \) succeeds in Experiment C.2 only if it holds that
which implies exactly one solution to the system of equations in Step 3 of our reduction when \(\mathcal{A} \) succeeds. It follows easily by inspection that Experiment C.3 outputs 1 if and only if Experiment C.2 outputs 1, and so the reduction is perfect. \(\square \)
It remains only to apply Lemma 3.7 (see Sect. 3.1), which asserts that any PPT algorithm that factors biprimes produced by  with adversarial shares can be used (with polynomial loss in the probability of success) to factor biprimes produced by
with adversarial shares can be used (with polynomial loss in the probability of success) to factor biprimes produced by  without adversarial shares. Thus, if we assume factoring biprimes from the distribution of
without adversarial shares. Thus, if we assume factoring biprimes from the distribution of  to be hard, then we must conclude that \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) are computationally indistinguishable.
to be hard, then we must conclude that \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) are computationally indistinguishable.
Hybrid \(\mathcal {H}_{4}\). This experiment is identical to \(\mathcal {H}_{3}\), except in the way that the privacy-preserving check is simulated in Step 7 of  (the privacy-free check is simulated as in \(\mathcal {H}_{3}\)). In \(\mathcal {H}_{3}\), the simulator emulates both
(the privacy-free check is simulated as in \(\mathcal {H}_{3}\)). In \(\mathcal {H}_{3}\), the simulator emulates both  and the honest parties internally, using its knowledge of \(p\) and \(q\). Specifically, in \(\mathcal {H}_{3}\), the emulated honest parties abort during the check if
and the honest parties internally, using its knowledge of \(p\) and \(q\). Specifically, in \(\mathcal {H}_{3}\), the emulated honest parties abort during the check if  or
or  for any \(i\in {{\varvec{\mathrm {P}}}^*} \), or if a \(\texttt {cheat}\) instruction was sent to
for any \(i\in {{\varvec{\mathrm {P}}}^*} \), or if a \(\texttt {cheat}\) instruction was sent to  at any point, or if
at any point, or if

In \(\mathcal {H}_{4}\), the simulator avoids using knowledge of \(p\) or \(q\) when the privacy-preserving check is run. It does not emulate the honest parties or  . The simulation instead aborts on behalf of the honest parties if \(N'\ne N\) or if there exists any \(j\in [\ell +1,{\ell '}]\) such that
. The simulation instead aborts on behalf of the honest parties if \(N'\ne N\) or if there exists any \(j\in [\ell +1,{\ell '}]\) such that
We will argue that this new predicate is equivalent to the former one.
First, consider a protocol state such that the check in Eq. 15 fails. Without loss of generality, assume that the first half (dealing with \(p\)) fails, but an analogous argument exists for \(q\). If we define a vector of offset values \({\varvec{\mathrm {p}}}^\Delta \) such that \({\varvec{\mathrm {p}}}^{\Delta }_{i,j}=({p_{i}} - {{\varvec{\mathrm {p}}}_{i,j}})\bmod {{\varvec{\mathrm {m}}} _{j}}\) for every \(i\in {{\varvec{\mathrm {P}}}^*} \) and \(j\in [\ell +1,{\ell '}]\), then it is clear that when the parties behave honestly, \({\varvec{\mathrm {p}}}^{\Delta }_{i,j} = 0\) for every pair (i, j). On the other hand, a violation of Eq. 15 implies that there must exist some pair (i, j) such that \({\varvec{\mathrm {p}}}^{\Delta }_{i,j}\ne 0\). If we let
and we define \({\varvec{\mathrm {p}}}^{\Delta }_{i,j} = 0\) for \(i\in {{\varvec{\mathrm {P}}}^*} \) and \(j\in [\ell ]\) then we find that

where it is certain that \(p_i<M\). Notice by inspection of the  algorithm that it must hold that
algorithm that it must hold that  . Since it also clearly holds that \(M'\equiv 0 \pmod {M}\), we can conclude that
. Since it also clearly holds that \(M'\equiv 0 \pmod {M}\), we can conclude that

where the equality is taken over the integers. Thus, if the check in Eq. 15 fails in \(\mathcal {H}_{4}\), causing \(\mathcal {H}_{4}\) to abort, then the range check in \(\mathcal {H}_{3}\) must also fail, causing \(\mathcal {H}_{3}\) to abort. The converse also holds: Since honest behavior cannot yield  , it must be the case that if the range check in \(\mathcal {H}_{3}\) fails, then there exists some (i, j) such that \({\varvec{\mathrm {p}}}^{\Delta }_{i,j}\ne 0\), and thus the check in Eq. 15 fails in \(\mathcal {H}_{4}\).
, it must be the case that if the range check in \(\mathcal {H}_{3}\) fails, then there exists some (i, j) such that \({\varvec{\mathrm {p}}}^{\Delta }_{i,j}\ne 0\), and thus the check in Eq. 15 fails in \(\mathcal {H}_{4}\).
Now, consider a protocol state such that the check in Eq. 15passes. It is easy to see that in this case

which trivially yields

and thus, we can conclude that the two predicates are equivalent, and \(\mathcal {H}_{4}\) is distributed identically to \(\mathcal {H}_{3}\).
Hybrid \(\mathcal {H}_{5}\). During the entire sequence of hybrids thus far, our simulator has played the role of  . In this hybrid, the simulator instead interacts with the real
. In this hybrid, the simulator instead interacts with the real  as a black box. In particular, whenever the simulator would have called
as a black box. In particular, whenever the simulator would have called  in \(\mathcal {H}_{4}\), it instead sends \((\texttt {adv-sample}, \mathsf {sid}, i, {p_{i}}, {q_{i}})\) to
in \(\mathcal {H}_{4}\), it instead sends \((\texttt {adv-sample}, \mathsf {sid}, i, {p_{i}}, {q_{i}})\) to  for every \(i\in {{\varvec{\mathrm {P}}}^*} \) in \(\mathcal {H}_{5}\). Whereas
for every \(i\in {{\varvec{\mathrm {P}}}^*} \) in \(\mathcal {H}_{5}\). Whereas  outputs factors of the candidate it sampled, regardless of whether that candidate is a biprime,
outputs factors of the candidate it sampled, regardless of whether that candidate is a biprime,  returns factors only if the candidate is not a biprime, and if the candidate is a biprime, then
returns factors only if the candidate is not a biprime, and if the candidate is a biprime, then  outputs the biprime itself.Footnote 21 Recall that in \(\mathcal {H}_{4}\), if the candidate is a biprime, and no cheating occurs, then the simulator does not use knowledge of the factors in its simulation. Thus, in \(\mathcal {H}_{5}\), it has enough information to simulate when
outputs the biprime itself.Footnote 21 Recall that in \(\mathcal {H}_{4}\), if the candidate is a biprime, and no cheating occurs, then the simulator does not use knowledge of the factors in its simulation. Thus, in \(\mathcal {H}_{5}\), it has enough information to simulate when  returns a biprime, until a cheat occurs. If a cheat occurs, and the simulator requires knowledge of the factors to continue, then the simulator sends \((\texttt {cheat},\mathsf {sid})\) to
returns a biprime, until a cheat occurs. If a cheat occurs, and the simulator requires knowledge of the factors to continue, then the simulator sends \((\texttt {cheat},\mathsf {sid})\) to  , which returns the factors and aborts. If no cheat occurs, then the simulator sends \((\texttt {proceed},\mathsf {sid})\) to
, which returns the factors and aborts. If no cheat occurs, then the simulator sends \((\texttt {proceed},\mathsf {sid})\) to  at the end of the simulation, so that it releases its output to the honest parties.
at the end of the simulation, so that it releases its output to the honest parties.
Since  simply calls
simply calls  internally, it is easy to see that \(\mathcal {H}_{5}\) is distributed identically to \(\mathcal {H}_{4}\). It is somewhat more difficult but nevertheless possible to see that our simulator is now identical to
internally, it is easy to see that \(\mathcal {H}_{5}\) is distributed identically to \(\mathcal {H}_{4}\). It is somewhat more difficult but nevertheless possible to see that our simulator is now identical to  as previously described; all remaining differences between the two are purely syntactic. Thus,
as previously described; all remaining differences between the two are purely syntactic. Thus,

and by the sequence of hybrids we have just shown, it holds that

for the adversary \(\mathcal{A} \) and all environments \(\mathcal{Z} \), assuming the hardness of factoring primes generated by  . \(\square \)
. \(\square \)
Rights and permissions
About this article
Cite this article
Chen, M., Doerner, J., Kondi, Y. et al. Multiparty Generation of an RSA Modulus. J Cryptol 35, 12 (2022). https://doi.org/10.1007/s00145-021-09395-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00145-021-09395-y


 are taken to be of length
are taken to be of length  for a detailed algorithm to sample such views.
for a detailed algorithm to sample such views. can never be triggered.
can never be triggered. to receive
to receive  .
. to sample an agreed-upon uniform vector
to sample an agreed-upon uniform vector  to decommit
to decommit  , and as a consequence, Bob receives
, and as a consequence, Bob receives  , it holds for all
, it holds for all  to decommit
to decommit  to abort. If the simulator continues past this point, it must be the case that either
to abort. If the simulator continues past this point, it must be the case that either  to abort.
to abort. abort if it lands on heads.
abort if it lands on heads. is triggered at the end of the simulation if and only if
is triggered at the end of the simulation if and only if  ) at at least
) at at least  as a consequence, Bob receives
as a consequence, Bob receives  instances associated with the session IDs in
instances associated with the session IDs in  . Bob verifies that for each
. Bob verifies that for each  before Step
before Step  , or if there is any
, or if there is any 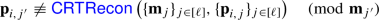
 before Step
before Step  , and if for all
, and if for all 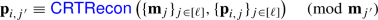
 ) to compute
) to compute 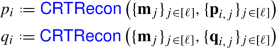
 internally, receives as output either
internally, receives as output either  and
and  samples from a distribution identical to that of
samples from a distribution identical to that of  , conditioned on honest behavior during the Candidate Sieving phase of the protocol. Consequently, it follows from the perfect security of additive secret sharing that
, conditioned on honest behavior during the Candidate Sieving phase of the protocol. Consequently, it follows from the perfect security of additive secret sharing that  will be
will be  returns
returns  .
. reports that
reports that  , the corrupt parties transmit values that add up to the expected sums), then the simulator outputs
, the corrupt parties transmit values that add up to the expected sums), then the simulator outputs  , and reports the same outcome to the corrupt parties if it receives
, and reports the same outcome to the corrupt parties if it receives  with
with  reports that
reports that  .
. reports that
reports that  .
. reports that
reports that  , as in
, as in