Everlasting Multi-party Computation

Abstract

A protocol has everlasting security if it is secure against adversaries that are computationally unlimited after the protocol execution. This models the fact that we cannot predict which cryptographic schemes will be broken, say, several decades after the protocol execution. In classical cryptography, everlasting security is difficult to achieve: even using trusted setup like common reference strings or signature cards, many tasks such as secure communication and oblivious transfer cannot be achieved with everlasting security. An analogous result in the quantum setting excludes protocols based on common reference strings, but not protocols using a signature card. We define a variant of the Universal Composability framework, everlasting quantum-UC, and show that in this model, we can implement secure communication and general multi-party computation using signature cards as trusted setup.

1 Introduction

Everlasting Security Computers and algorithms improve over time and so does the ability of an adversary to break cryptographic complexity assumptions and protocols. It may be feasible to make a good estimate as to which computational problems are hard today, and which encryption schemes unbroken. But it is very difficult to make more than an educated guess as to which cryptographic schemes will be secure, say, ten years from now. Key length recommendations (e.g., [3, 15, 29]) can only be made based on the assumption that progress continues at a similar rate as today; unexpected algorithmic progress and future technologies like quantum computers can render even the most paranoid choices for the key length obsolete.

This situation is very problematic if we wish to run cryptographic protocols on highly sensitive data such as medical or financial data or government secrets. Such data often has to stay confidential for many decades. But an adversary might intercept messages from a protocol that is secure today, store them, and some decades later, when the underlying cryptosystems have been broken, decrypt them. For highly sensitive data, this would not be an acceptable risk.

One way out is to use protocols with unconditional (information-theoretical) security that are not based on any computational hardness assumptions. For many tasks, however, unconditionally secure protocols simply do not exist (in particular if we cannot assume a majority of honest participants). A compromise is the concept of everlasting security. In a nutshell, a protocol is everlastingly secure if it cannot be broken by an adversary that becomes computationally unlimited after the protocol execution. This guarantees that all assumptions need only to hold during the protocol execution, sensitive data is not threatened by possible future attacks on today’s schemes. We only need to reliably judge the current state of the art, not future technologies.

Unfortunately, also for everlasting security, we have strong impossibility results. It is straightforward to see that everlastingly secure public key encryption is not possible, symmetric encryption needs keys as long as the transmitted messages, and most secure multi-party computations (MPC) are impossible (e.g., oblivious transfer, see Sect. 4).

Quantum Cryptography Since the inception of quantum key distribution (QKD) by Bennett and Brassard [2], it has been known that quantum cryptography can achieve tasks that are impossible in a classical setting: a shared key can be agreed upon between two parties such that even a computationally unlimited eavesdropper does not learn that key. Classically, this is easily seen to be impossible. Crépeau and Kilian [11] showed how, given only a commitment scheme, we can securely realize an oblivious transfer (OT), which in turn, using ideas from Kilian [23] can be used to implement arbitrary unconditionally secure MPC. Classically, given only a commitment, it is impossible to construct arbitrary unconditionally secure MPC (or even everlastingly secure ones, see Sect. 4). Initial enthusiasm was, however, dampened by strong impossibility results. Mayers [26] showed that it is impossible to construct an unconditionally secure commitment from scratch. Similar impossibilities hold for OT and many other function evaluations (Lo [24]). So the goal to get unconditionally secure MPC is not achievable, even with quantum cryptography.

Also, the usefulness of QKD has been challenged (e.g., by Bernstein [5], who also raises other concerns than the following). To run a QKD protocol, an authenticated channel is needed. But how to implement such a channel? If we use a public key infrastructure for signing messages, we lose unconditional security and thus the main advantage of QKD. If we use shared key authentication, a key needs to be exchanged beforehand. (And, if we exchange an authentication key in a personal meeting, why not just exchange enough key material for one-time pad encryption—storage is cheap.)

Everlasting Quantum Security A simple change of focus resolves the problems described in the previous paragraph. Instead of seeing the goal of quantum cryptography in achieving unconditional security, we can see it as achieving everlasting security. For example, if we run a QKD protocol and authenticate all messages using signatures and a public key infrastructure, then we do not get an unconditionally secure protocol, but we do get everlasting security: only the signatures are vulnerable to unlimited adversaries, but breaking the security of the signatures after the protocol execution does not help the adversary to recover the key. (Experience and the discussion on composition below show that one has to be careful: we need to check that signatures and QKD indeed play together well and compose securely. We answer this positively in Sect. 5: we achieve everlastingly secure universally composable security.)

What about secure MPC? Recall that for constructing unconditionally secure MPC in the quantum setting, the only missing ingredient was a commitment. Once we have a commitment, unconditionally secure MPC protocols exist [34]. Unconditionally secure commitments do not exist, but everlastingly secure ones do! Consider a statistically hiding commitment. That is, the binding property may be subject to computational assumptions, but the hiding property holds with respect to unlimited adversaries. Such a scheme is in fact everlastingly secure. Being able to break the binding property of a commitment after the protocol end is of no use—the recipient of the commitment is not listening any more. And the hiding property, i.e., the secrecy of the committed data, holds forever. So a statistically hiding commitment is in fact everlastingly secure. It seems that we have all ingredients for everlastingly secure quantum MPC. The next paragraph, however, shows that the situation is considerably more subtle.

We stress that neither the concept of everlasting security nor the idea of combining it with quantum cryptography is original to this paper. For example, [1] already suggested to combine QKD with computational authenticated, albeit without proof or analysis of composition problems.

Everlasting Security and Composition—A Ccautionary Tale As discussed above, statistically hiding commitments are in fact everlastingly secure, and there are quantum protocols that construct unconditionally secure OT (among other things). Thus, composing a statistically hiding commitment with such a protocol will give us an everlastingly secure OT in the bare model (i.e., not using any trusted setup). But it turns out that this reasoning is wrong! Lo’s impossibility of OT [24] can be easily modified to show that unconditional OT is impossible, even if we consider only passive (semi-honest) adversaries. But everlasting security implies unconditional security against passive adversaries: A passive adversary is one that during the protocol follows the protocol (and thus in particular is computationally bounded) but after the protocol may perform unlimited computations. Thus, Lo’s impossibility excludes the existence of everlastingly secure OTs.

What happened? The problem is that although statistically hiding commitments are everlastingly secure on their own, they lose their security when composed. Composition problems are common in cryptography, but we find this case particularly instructive: the commitment does not lose its security only when composed with some contrived protocol, but instead in a natural construction. And not only does a particular construction break down, we are faced with a general impossibility. And the resulting protocol is insecure in a strong sense: an unlimited adversary can guess either Alice’s or Bob’s input. (As opposed to a situation where the “break” consists solely of the nonexistence of a required simulator.)

One may be tempted to suggest that the failure is not related to the everlasting security, but to the non-composability of the commitments. Damgård and Nielsen [14] present commitment schemes that are universally composable (we elaborate on this notion below, it is a security notion that essentially guarantees “worry-free” composition), that only need a predistributed common reference strings (CRS), and that are statistically hiding.¹ Yet, when using these commitments to get everlastingly secure OT, we run into the same problem again: we would get an everlastingly secure OT using a CRS, but a generalization of Lo’s impossibility shows that no everlastingly secure OT protocols exist even given a CRS (see Sect. 4).²

Quantum Everlasting Universal Composability The preceding paragraph shows that, in the setting of everlasting security, it is vital to find definitions that guarantee composability. One salient approach is the Universal Composability (UC) framework by Canetti [7]. In the UC framework, we compare a protocol $\pi$ against a so-called ideal functionality $\mathcal F$ which describes what $\pi$ should ideally do. (E.g., $\mathcal F$ could be a commitment functionality that registers the value Alice commits to, but forwards it to Bob only when Alice requests an open.) We say $\pi$ UC emulates $\mathcal F$ if for any adversary $\mathrm {Adv}$ (that attacks $\pi$) there is a simulator $\mathrm {Sim}$ (that “attacks” $\mathcal F$) such that no machine $\mathcal Z$ (the environment) can distinguish $\pi$ running with $\mathrm {Adv}$ (real model) from $\mathcal F$ running with $\mathrm {Sim}$ (ideal model). The intuition behind this is that $\mathrm {Adv}$ can perform only attacks that can be mimicked by $\mathrm {Sim}$. Since $\mathcal F$ is secure by definition, $\mathrm {Adv}$ can perform no “harmful” attacks. A salient property of the UC framework is that UC secure protocols can be composed in arbitrary ways (universal composition). By tweaking the details of the definition, we get various variants of UC: if $\mathcal Z$, $\mathrm {Sim}$, $\mathrm {Adv}$ are polynomial-time, we have computational UC. If they are unlimited, statistical UC (modeling unconditional security). Unlimited quantum machines lead to the definition of statistical quantum-UC [34].

Müller-Quade and Unruh [27] showed that the UC framework can also be adapted to the setting of everlasting security: we quantify over $\mathcal Z$, $\mathrm {Sim}$, $\mathrm {Adv}$ that are polynomial-time, but we say that $\mathcal Z$ distinguishes the real and ideal model if the distribution of $\mathcal Z$’s output is not statistically indistinguishable. That is, a protocol is considered insecure if one can distinguish real and ideal model when being polynomial-time during the protocol, but unlimited afterward (statistical indistinguishability means that no unlimited machine can distinguish).

The ideas from [27] can be easily adapted to the quantum case. In Sect. 3, we introduce everlasting quantum-UC (eqUC). Here $\mathcal Z$, $\mathrm {Sim}$, $\mathrm {Adv}$ are quantum-polynomial-time machines (representing the fact that adversaries are limited during the protocol run), but we require that the quantum state output by $\mathcal Z$ in the real and ideal model is trace-indistinguishable (two quantum states are trace-indistinguishable iff no unlimited quantum machine can distinguish them). The eqUC-security notion inherits all composability properties from the UC notion. Also, protocols that are secure with respect to statistical classical or statistical quantum-UC are also eqUC-secure. In particular, known quantum protocols for constructing MPC from commitments [34] are also eqUC-secure.³ Thus, if we find an eqUC-secure commitment protocol, we immediately get eqUC-secure MPC protocols by composition.

Everlasting Quantum-UC Commitments The problem of everlasting UC commitments in the classical setting was already studied in [27]. Their protocol uses a signature card as trusted setup.⁴ Here a signature card is a trusted device (modeled as a functionality) such that the owner of the card can sign messages, everyone can access the public key, and no-one (not even the owner) can get the secret key.⁵ Their protocol is, however, only known to be secure in the classical setting. In fact, when we try to prove the protocol secure in a quantum setting, we stumble upon an interesting difficulty in the interplay of zero-knowledge proofs of knowledge and signature schemes.

A core step in the protocol is that Alice performs a proof of knowledge P showing that she knows a certain signature $\sigma$. In the security proof, we then show that Alice must have obtained $\sigma$ from the signature card: assume Alice successfully performs P without requesting $\sigma$ first. Since P is a proof of knowledge, there is an extractor E (using Alice and indirectly the signing oracle as a black box) that returns a valid witness, i.e., the signature $\sigma$. Since E returns the signature without requesting it from the signing oracle, we have a contradiction to the unforgeability of the signature scheme.

It seems that the same reasoning applies against quantum adversaries if we use quantum proofs of knowledge instead. Unfortunately, this is not the case. In a quantum proof of knowledge (as defined by Unruh [36]), an extractor with black-box access to the prover executes both the prover (modeled as a unitary operation) as well as its inverse (i.e., the inverse of that unitary). This is the quantum analogue of classical rewinding. So the extractor E will invoke not only the signing oracle, but also its inverse! But unforgeability will not guarantee that there are no forgeries when the adversary accesses the inverse of the signing oracle. Hence, the security proof fails.

To avoid this problem, we need a new protocol which does not require rewinding in the same places of the security proof where we use the unforgeability of the signature scheme. We present such a protocol; it is considerably more involved than the one from [27]. We believe that our approach is of independent interest because it shows one way around the limitations of quantum proofs of knowledge.

Bounded Quantum Storage Model We quickly compare the concept of everlasting security in this paper with the bounded quantum storage model (BQSM; [13]). The BQSM achieves very similar goals. Security in the BQSM guarantees that the protocol cannot be broken by an adversary that has limited quantum memory during the protocol execution and unlimited quantum memory after the execution. The BQSM is thus analogous to everlasting security as discussed here, except that it considers quantum memory where we consider computational power. The advantage of the BQSM over our model is that when using a BQSM protocol, we only need to make assumptions about the power of the adversary (its quantum memory). In contrast, in our model we need to assume that the computational power is limited and that certain mathematical problems are hard. In our view, the main disadvantage of the BQSM is that it might be useful only for a limited time: currently, we may assume a small limit on the adversary’s quantum memory. Should quantum technology advance, though, quantum memory might become cheap, and at that point BQSM protocols must not be used any more. In contrast, with everlasting security as in this paper, if an assumption we use in a protocol is broken, it is likely that there still are other assumptions that can be used—we can then fix the protocol by switching the underlying problem. Also, BQSM protocols tend to have a high communication complexity, and composition is more involved (in particular when we wish for universal composability [35]). Then again, our approach requires trusted setup (signature cards). An interesting goal would be protocols that are simultaneously secure in our model and the BQSM.

In the classical setting, the bounded storage model can also be used [25] but has very high communication complexity (quadratic in the memory bound). [18] shows that if we combine bounded storage with temporary computational assumptions, then in the random oracle model we can achieve lower communication complexity (but they also show impossibilities when not using the random oracle model). In contrast, our work uses quantum communication and temporary computational assumptions, but no bounded storage.

Further Related Work [8] also considers the problem of using an unconditionally hiding computationally binding commitment to construct a quantum OT (as opposed to using directly a functionality). They show that with such a commitment, OT can be realized (no impossibility results are given). However, their OT protocol only computationally hides the sender’s inputs (although one may be tempted to assume otherwise as the commitments that are used are unconditionally hiding). In fact, our impossibility results imply that their OT cannot be everlastingly secure.

Organization & Contribution In Sect. 3 we present the everlasting quantum-UC model and the corresponding composition theorem. In Sect. 4 we show the impossibility of everlastingly secure OT in the classical and the quantum setting using various functionalities. In Sect. 5 we show that using signature cards or a public key infrastructure, an everlastingly quantum-UC-secure channel can be implemented. In Sect. 6 we show how to implement arbitrary everlastingly quantum-UC-secure multi-party computation using signature cards.

2 Preliminaries

General A nonnegative function $\mu$ is called negligible if for all $c>0$ and all sufficiently large k, $\mu (k)<k^{-c}$. A nonnegative function f is called overwhelming if $f\ge 1-\mu$ for some negligible $\mu$. Keywords in typewriter font (e.g., environment) are assumed to be fixed but arbitrary distinct non-empty words in $\{0,1\}^{*}$. $\varepsilon \in \{0,1\}^{*}$ denotes the empty word. Given a sequence $x=x_1,\dots , x_n$, and a set $I\subseteq \{1,\dots ,n\}$, $x_{|I}$ denote the sequence x restricted to the indices $i\in I$.

Quantum Systems We can only give a terse overview over the formalism used in quantum computing. For a thorough introduction, we recommend the textbook by Nielsen and Chuang [28, Chap. 1–2]. A (pure) state in a quantum system is described by a vector ${\left| {\psi }\right\rangle }$ in some Hilbert space $\mathcal H$. In this work, we only use Hilbert spaces of the form $\mathcal H=\mathbb {C}^N$ for some countable set N, usually $N=\{0,1\}$ for qubits or $N=\{0,1\}^{*}$ for bitstrings. We always assume a designated orthonormal basis $\{{\left| {x}\right\rangle }:x\in N\}$ for each Hilbert space, called the computational basis. The basis states ${\left| {x}\right\rangle }$ represent classical states (i.e., states without superposition). Given several separate subsystems $\mathcal H_1=\mathbb {C}^{N_1},\dots ,\mathcal H_n=\mathbb {C}^{N_n}$, we describe the joint system by the tensor product $\mathcal H_1\otimes \dots \otimes \mathcal H_n=\mathbb {C}^{N_1\times \dots \times N_n}$. We write ${\left\langle {\Psi }\right| }$ for the linear transformation mapping ${\left| {\Phi }\right\rangle }$ to the scalar product $\langle \Psi \vert \Phi \rangle$. Consequently, ${\left| {\Psi }\right\rangle }{\left\langle {\Psi }\right| }$ denotes the orthogonal projector on ${\left| {\Psi }\right\rangle }$. We set ${\left| {0}\right\rangle }_+:={\left| {0}\right\rangle }$, ${\left| {1}\right\rangle }_+:={\left| {1}\right\rangle }$, ${\left| {0}\right\rangle }_\times :=\frac{1}{\sqrt{2}}({\left| {0}\right\rangle }+{\left| {1}\right\rangle })$, and ${\left| {1}\right\rangle }_\times :=\frac{1}{\sqrt{2}}({\left| {0}\right\rangle }-{\left| {1}\right\rangle })$. For $x\in \{0,1\}^{n}$ and $\theta \in \{+,\times \}^n$, we define ${\left| {x}\right\rangle }_\theta :={\left| {x_1}\right\rangle }_{\theta _1}\otimes \dots \otimes {\left| {x_n}\right\rangle }_{\theta _n}$.

Mixed States If a system is not in a single pure state, but instead is in the pure state ${\left| {\Psi _i}\right\rangle }\in \mathcal H$ with probability $p_i$ (i.e., it is in a mixed state), we describe the system by a density operator $\rho =\sum _i p_i{\left| {\Psi _i}\right\rangle }{\left\langle {\Psi _i}\right| }$ over $\mathcal H$. This representation contains all physically observable information about the distribution of states, but some distributions are not distinguishable by any measurement and thus are represented by the same mixed state. The set of all density operators is the set of all positive⁶ operators $\mathcal H$ with trace 1 and is denoted $\mathcal P(\mathcal H)$. Composed systems are described by operators in $\mathcal P(\mathcal H_1\otimes \dots \otimes \mathcal H_n)$. In the following, when speaking about (quantum) states, we always mean mixed states in the density operator representation. A mapping $\mathcal E:\mathcal P(\mathcal H_1)\rightarrow \mathcal P(\mathcal H_2)$ represents a physically possible operation (realizable by a sequence of unitary transformations, measurements, and initializations and removals of qubits) iff it is a completely positive trace preserving map.⁷ We call such mappings superoperators. The superoperator $\mathcal E_{{ init }}^m$ on $\mathcal P(\mathcal H)$ with $\mathcal H:=\mathbb {C}^{\{0,1\}^{*}}$ and $m\in \{0,1\}^{*}$ is defined by $\mathcal E_{{ init }}^m(\rho ):={\left| {m}\right\rangle }{\left\langle {m}\right| }$ for all $\rho$. By ${\mathrm {TD}}(\rho ,\rho ')$ we denote the trace distance between $\rho$ and $\rho '$. Intuitively, the trace distance is the probability with which an unlimited distinguisher can distinguish $\rho$ and $\rho '$ with a single measurement.

Composed Systems Given a superoperator $\mathcal E$ on $\mathcal P(\mathcal H_1)$, the superoperator $\mathcal E\otimes id$ operates on $\mathcal P(\mathcal H_1\otimes \mathcal H_2)$. Instead of saying “we apply $\mathcal E\otimes id$,” we say “we apply $\mathcal E$ to $\mathcal H_1$.” If we say “we initialize $\mathcal H$ with m,” we mean “we apply $\mathcal E_{{ init }}^m$ to $\mathcal H$.” Given a state $\rho \in \mathcal P(\mathcal H_1\otimes \mathcal H_2)$, let $\rho _x:=({\left| {x}\right\rangle }{\left\langle {x}\right| }\otimes id )\rho ({\left| {x}\right\rangle }{\left\langle {x}\right| }\otimes id )$. Then the outcome of measuring $\mathcal H_1$ in the computational basis is x with probability ${{\mathrm{tr}}}\rho _x$, and after measuring x, the quantum state is $\frac{\rho _x}{{{\mathrm{tr}}}\rho _x}$. Since we will only perform measurements in the computational basis in this work, we will omit the qualification “in the computational basis.” The terminology in this paragraph generalizes to systems composed of more than two subsystems.

Classical States Classical probability distributions $P:N\rightarrow [0,1]$ over a countable set N are represented by density operators $\rho \in \mathcal P(\mathbb {C}^N)$ with $\rho =\sum _{x\in N}P(x){\left| {x}\right\rangle }{\left\langle {x}\right| }$ where $\{{\left| {x}\right\rangle }\}$ is the computational basis. We call a state classical if it is of this form. We thus have a canonical isomorphism between the classical states over $\mathbb {C}^N$ and the probability distributions over N. We call a superoperator $\mathcal E:\mathcal P(\mathbb {C}^{N_1})\rightarrow \mathcal P(\mathbb {C}^{N_2})$ classical iff there is a randomized function $F:N_1\rightarrow N_2$ such that $\mathcal E(\rho )=\sum _{{\begin{array}{c} x\in N_1\\ y\in N_2 \end{array}}}\Pr [F(x)=y]\cdot {\left\langle {x}\right| }\rho {\left| {x}\right\rangle }\cdot {\left| {y}\right\rangle }{\left\langle {y}\right| }$. Classical superoperators describe what can be realized with classical computations. An example of a classical superoperator on $\mathcal P(\mathbb {C}^N)$ is $\mathcal E_{{ class }}:\rho \mapsto \sum _x{\left\langle {x}\right| }\rho {\left| {x}\right\rangle }\cdot {\left| {x}\right\rangle }{\left\langle {x}\right| }$. Intuitively, $\mathcal E_{{ class }}$ measures $\rho$ in the computational basis and then discards the outcome, thus removing all superpositions from $\rho$.

3 Everlasting Quantum-UC

We now present our everlasting quantum-UC-framework. Our definition is based on the modeling of UC in the quantum case from [34]. For a reader familiar with their definition: the new concepts in this section are the definition of $\mathrm {QExec}$ (Page 10), of trace-indistinguishability (Page 10), and of everlasting quantum-UC (Definition 3).

3.1 The Basic Model

Machine Model A machine M is described by an identity $id _M$ in $\{0,1\}^{*}$ and a sequence of superoperators $\mathcal {E}^{(\eta )}_{M}$ ($\eta \in \mathbb {N}$) on $\mathcal H^{{ \mathrm state }}\otimes \mathcal H^{{ \mathrm class }}\otimes \mathcal H^{{ \mathrm quant }}$ with $\mathcal H^{{ \mathrm state }},\mathcal H^{{ \mathrm class }},\mathcal H^{{ \mathrm quant }}:=\mathbb {C}^{\{0,1\}^{*}}$ (the state transition operators). The index $\eta$ in $\mathcal {E}^{(\eta )}_{M}$ denotes the security parameter. The Hilbert space $\mathcal H^{{ \mathrm state }}$ represents the state kept by the machine between invocations, and $\mathcal H^{{ \mathrm class }}$ and $\mathcal H^{{ \mathrm quant }}$ are used both for incoming and outgoing messages. Any message consists of a classical part stored in $\mathcal H^{{ \mathrm class }}$ and a quantum part stored in $\mathcal H^{{ \mathrm quant }}$. If a machine $id _{ sender }$ wishes to send a message with classical part m and quantum part ${\left| {\Psi }\right\rangle }$ to a machine $id _{ rcpt }$, the machine $id _{ sender }$ initializes $\mathcal H^{{ \mathrm class }}$ with $( id _{ sender }, id _{ rcpt },m)$ and $\mathcal H^{{ \mathrm quant }}$ with ${\left| {\Psi }\right\rangle }$. (See the definition of the network execution below for details.) The separation of messages into a classical and a quantum part is for clarity only, all information could also be encoded directly in a single register. If a machine does not wish to send a message, it initializes $\mathcal H^{{ \mathrm class }}$ and $\mathcal H^{{ \mathrm quant }}$ with $\varepsilon$.

A network $\mathbf N$ is a set of machines with pairwise distinct identities containing a machine $\mathcal Z$ with $id _\mathcal Z=\mathtt {environment}$. We write $ids _\mathbf N$ for the set of the identities of the machines in $\mathbf N$.

We call a machine M quantum-polynomial-time if there is a uniform⁸ sequence of quantum circuits $C_\eta$ such that for all $\eta$, the circuit $C_\eta$ implements the superoperator $\mathcal {E}^{(\eta )}_{M}$.

Network Execution The state space $\mathcal H_\mathbf N$ of a network $\mathbf N$ is defined as $\mathcal H_\mathbf N:= \mathcal H^{{ \mathrm class }}\otimes \mathcal H^{{ \mathrm quant }}\otimes \bigotimes _{ id \in ids _\mathbf N}\mathcal H^{{ \mathrm state }}_ id$ with $\mathcal H^{{ \mathrm state }}_ id ,\mathcal H^{{ \mathrm class }},\mathcal H^{{ \mathrm quant }}:=\mathbb {C}^{\{0,1\}^{*}}$. Here $\mathcal H^{{ \mathrm state }}_ id$ represents the local state of the machine with identity $id$ and $\mathcal H^{{ \mathrm class }}$ and $\mathcal H^{{ \mathrm quant }}$ represent the state spaces used for communication. ($\mathcal H^{{ \mathrm class }}$ and $\mathcal H^{{ \mathrm quant }}$ are shared between all machines. Since only one machine is active at a time, no conflicts occur.)

A step in the execution of $\mathbf N$ is defined by a superoperator $\mathcal E:=\mathcal {E}^{(k)}_{\mathbf N}$ operating on $\mathcal H_\mathbf N$. This superoperator performs the following steps: first, $\mathcal E$ measures $\mathcal H^{{ \mathrm class }}$ in the computational basis and parses the outcome as $( id _{{{ \mathrm sender }}}, id _{{ rcpt }},m)$. Let M be the machine in $\mathbf N$ with identity $id _{ rcpt }$. Then $\mathcal E$ applies $\mathcal {E}^{(\eta )}_{M}$ to $\mathcal H^{{ \mathrm state }}_{ id _{{ rcpt }}}\otimes \mathcal H^{{ \mathrm class }}\otimes \mathcal H^{{ \mathrm quant }}$. Then $\mathcal E$ measures $\mathcal H^{{ \mathrm class }}$ and parses the outcome as $( id _{{{ \mathrm sender }}}', id _{{ rcpt }}',m')$. If the outcome could not be parsed, or if $id _{{{ \mathrm sender }}}'\ne id _{{ rcpt }}$, initialize $\mathcal H^{{ \mathrm class }}$ with ${(\varepsilon ,\mathtt {environment},\varepsilon )}$ and $\mathcal H^{{ \mathrm quant }}$ with $\varepsilon$. (This ensures that the environment is activated if a machine sends no or an ill-formed message.)

The output of the network $\mathbf N$ on input z and security parameter $\eta$ is described by the following algorithm: let $\rho \in \mathcal P(\mathcal H_\mathbf N)$ be the state that is initialized to ${(\varepsilon ,\mathtt {environment},z)}$ in $\mathcal H^{{ \mathrm class }}$, and to the empty word $\varepsilon$ in all other registers. Then repeat the following two steps indefinitely: apply $\mathcal {E}^{(k)}_{\mathbf N}$ to $\rho$. Measure $\mathcal H^{{ \mathrm class }}$. If the outcome is of the form $(\mathtt {environment},\varepsilon , out )$, return $out$ and terminate. Otherwise, continue the loop. The probability distribution of the return value $out$ is denoted by $\mathrm {Exec}_\mathbf N(\eta ,z)$.

Furthermore, by $\mathrm {QExec}_\mathbf N(\eta ,z)$, we denote the state of the environment after sending $out$. That is, $\mathrm {QExec}_\mathbf N(\eta ,z)$ is the density operator resulting from tracing out all systems except $\mathcal H^{{ \mathrm state }}_\mathtt {environment}$ from $\rho$.

Corruptions To model corruptions, we introduce corrupted parties, special machines that follow the instructions given by the adversary. When invoked, the corrupted party $P^C_ id$ with identity $id$ measures $\mathcal H^{{ \mathrm class }}$ and parses the outcome as $( id _{{{ \mathrm sender }}}, id _{{ rcpt }},m)$. If $id _{{{ \mathrm sender }}}=\mathtt {adversary}$, $\mathcal H^{{ \mathrm class }}$ is initialized with m. (In this case, m specifies both the message and the sender/recipient. Thus, the adversary can instruct a corrupted party to send to arbitrary recipients.) Otherwise, $\mathcal H^{{ \mathrm class }}$ is initialized with $( id ,\mathtt {adversary},( id _{{{ \mathrm sender }}}, id _{{ rcpt }},m))$. (The message is forwarded to the adversary.) Note that, since $P^C_ id$ does not touch the $\mathcal H^{{ \mathrm quant }}$, the quantum part of the message is forwarded.

Given a network $\mathbf N$, and a set of identities C, we write $\mathbf N^C$ for the set resulting from replacing each machine $M\in \mathbf N$ with identity $id \in C$ by $P^C_ id$.

Security Model A protocol $\pi$ is a set of machines with $\mathtt {environment},\mathtt {adversary}\notin ids (\pi )$. We assume a set of identities $parties _\pi \subseteq ids (\pi )$ to be associated with $\pi$. $parties _\pi$ denotes which of the machines in the protocol are actually protocol parties (as opposed to incorruptible entities such as ideal functionalities).

An environment is a machine with identity $\mathtt {environment}$, an adversary or a simulator is a machine with identity $\mathtt {adversary}$ (there is no formal distinction between adversaries and simulators, the two terms refer to different intended roles of a machine).

In the following we call two networks $\mathbf N,\mathbf N'$ indistinguishable if there is a negligible function $\mu$ such that for all $z\in \{0,1\}^{*}$ and $\eta \in \mathbb {N}$, $| \Pr [\mathrm {Exec}_\mathbf N(\eta ,z)=1] - \Pr [\mathrm {Exec}_{\mathbf N'}(\eta ,z)=1] | \le \mu (\eta )$. We speak of perfect indistinguishability if $\mu =0$.

We call two networks $\mathbf N,\mathbf N'$ trace-indistinguishable if there is a negligible function $\mu$ such that for all $z\in \{0,1\}^{*}$ and $\eta \in \mathbb {N}$, ${\mathrm {TD}}( \mathrm {QExec}_\mathbf N(\eta ,z), \mathrm {QExec}_{\mathbf N'}(\eta ,z) ) \le \mu (\eta )$. We speak of perfect trace-indistinguishability if $\mu =0$.

Definition 1

(Statistical quantum-UC-security) Let protocols $\pi$ and $\rho$ be given. We say $\pi$ statistically quantum-UC emulates $\rho$ iff for every set $C\subseteq parties _\pi$ and for every adversary $\mathrm {Adv}$ there is a simulator $\mathrm {Sim}$ such that for every environment $\mathcal Z$, the networks $\pi ^C\cup \{\mathrm {Adv},\mathcal Z\}$ (called the real model) and $\rho ^C\cup \{\mathrm {Sim},\mathcal Z\}$ (called the ideal model) are indistinguishable. We furthermore require that if $\mathrm {Adv}$ is quantum-polynomial-time, so is $\mathrm {Sim}$.

Definition 2

(Computational quantum-UC-security) Let protocols $\pi$ and $\rho$ be given. We say $\pi$ computationally quantum-UC emulates $\rho$ iff for every set $C\subseteq parties _\pi$ and for every quantum-polynomial-time adversary $\mathrm {Adv}$ there is a quantum-polynomial-time simulator $\mathrm {Sim}$ such that for every quantum-polynomial-time environment $\mathcal Z$, the networks $\pi ^C\cup \{\mathrm {Adv},\mathcal Z\}$ and $\rho ^C\cup \{\mathrm {Sim},\mathcal Z\}$ are indistinguishable.

We can now define everlasting quantum-UC-security. The fact that in this definition, we require the networks to be trace-indistinguishable (i.e., even an unlimited machine cannot distinguish the output states of $\mathcal Z$ in real and ideal model), models the fact that in everlasting security, we allow unlimited computations after the protocol execution. During the protocol execution, environment, adversary, and simulator are quantum-polynomial-time.

Definition 3

(Everlasting quantum-UC-security) Let protocols $\pi$ and $\rho$ be given. We say $\pi$ everlastingly quantum-UC emulates (short eqUC emulates) $\rho$ iff for every set $C\subseteq parties _\pi$ and for every quantum-polynomial-time adversary $\mathrm {Adv}$ there is a quantum-polynomial-time simulator $\mathrm {Sim}$ such that for every quantum-polynomial-time environment $\mathcal Z$, the networks $\pi ^C\cup \{\mathrm {Adv},\mathcal Z\}$ and $\rho ^C\cup \{\mathrm {Sim},\mathcal Z\}$ are trace-indistinguishable.

Note that although $\mathrm {Exec}_{\pi ^C\cup \{\mathrm {Adv},\mathcal Z\}}(\eta ,z)$ may return arbitrary bitstrings, we only compare whether the return value of $\mathcal Z$ is 1 or not. This effectively restricts $\mathcal Z$ to returning a single bit. This can be done without loss of generality (see [7] for a discussion of this issue; their arguments also apply to the quantum case) and simplifies the definition.

In our framework, any communication between two parties is perfectly secure since the network model guarantees that they are delivered to the right party and not leaked to the adversary. To model a protocol with insecure channels instead, one would explicitly instruct the protocol parties to send all messages through the adversary. Authenticated channels can be realized by introducing an ideal functionality (see the next section) that realizes an authenticated channel. For simplicity, we only consider protocols with secure channels in this work.

Lemma 1

Let $\pi$ and $\rho$ be protocols. If $\pi$ statistically quantum-UC emulates $\rho$, then $\pi$ eqUC emulates $\rho$.

If $\pi$ eqUC emulates $\rho$, then $\pi$ computationally quantum-UC emulates $\rho$.

If non-uniformly quantum one-way functions and non-uniformly quantum pseudo-random generators exist, these implications are strict.

Proof

The implications are immediate from the definitions.

To show that the implications are strict, let f be a non-uniform quantum one-way function, and let $G:\{0,1\}^{\ell }\rightarrow \{0,1\}^{\ell +1}$ be a non-uniform quantum pseudo-random generator (here $\ell$ may depends on the security parameter).

Consider the following two one-party protocols: in protocol $\pi _1$, Alice outputs f(m) for uniformly random $m\in \{0,1\}^{\eta }$ to the environment. When receiving $m'$ with $f(m')=f(m)$ from the environment she answers with 1. In protocol $\rho _1$, Alice outputs a f(m) for uniformly random $m\in \{0,1\}^{\eta }$ to the environment. $\pi _1$ does not statistically UC emulate $\rho _1$: the distinguishing environment just sends a preimage of f(m) to Alice. But $\pi _1$ eqUC emulates $\rho _1$: for adversary $\mathrm {Adv}$, we use simulator $\mathrm {Sim}:=\mathrm {Adv}$, a polynomial-time environment will make Alice send 1 only with negligible probability. Thus, the first implication is strict.

Consider the following two one-party protocols: in protocol $\pi _2$, Alice sends $r:=G(m)$ for uniformly random $m\in \{0,1\}^{\ell }$ to the environment. In protocol $\rho _2$, Alice sends a uniformly random $r\in \{0,1\}^{\ell +1}$. $\pi _2$ does not eqUC emulate $\rho _2$: in $\rho _2$, with probability at least $\frac{1}{2}$, r will not be in the range of G, so to distinguish the environment just outputs r in its final output. But $\pi _2$ computationally quantum-UC emulates $\rho _2$, since the environment cannot distinguish between pseudo-random and random r. Thus, the second implication is strict. $\square$

3.2 Ideal Functionalities

In most cases, the behavior of the ideal model is described by a single machine $\mathcal F$ , the so-called ideal functionality. We can think of this functionality as a trusted third party that perfectly implements the desired protocol behavior. For example, the functionality $\mathcal F_\mathrm {OT}$ for oblivious transfer would take as input from Alice two bitstrings $m_0,m_1$, and from Bob a bit c, and send to Bob the bitstring $m_c$. Obviously, such a functionality constitutes a secure oblivious transfer. We can thus define a protocol $\pi$ to be a secure OT protocol if $\pi$ quantum-UC emulates $\mathcal F_\mathrm {OT}$ where $\mathcal F_\mathrm {OT}$ denotes the protocol consisting only of one machine, the functionality $\mathcal F_\mathrm {OT}$ itself. There is, however, one technical difficulty here. In the real protocol $\pi$, the bitstring $m_c$ is sent to the environment $\mathcal Z$ by Bob, while in the ideal model, $m_c$ is sent by the functionality. Since every message is tagged with the sender of that message, $\mathcal Z$ can distinguish between the real and the ideal model merely by looking at the sender of $m_c$. To solve this issue, we need to ensure that $\mathcal F$ sends the message $m_c$ in the name of Bob (and for analogous reasons, that $\mathcal F$ receives messages sent by $\mathcal Z$ to Alice or Bob). To achieve this, we use so-called dummy-parties [7] in the ideal model. These are parties with the identities of Alice and Bob that just forward messages between the functionality and the environment.

Definition 4

(Dummy-party) Let a machine P and a functionality $\mathcal F$ be given. The dummy-party $\tilde{P}$ for P and $\mathcal F$ is a machine that has the same identity as P and has the following state transition operator: let $id _\mathcal F$ be the identity of $\mathcal F$. When activated, measure $\mathcal H^{{ \mathrm class }}$. If the outcome of the measurement is of the form $(\mathtt {environment}, id _P,m)$, initialize $\mathcal H^{{ \mathrm class }}$ with $( id _P, id _\mathcal F,m)$. If the outcome is of the form $( id _\mathcal F, id _P,m)$, initialize $\mathcal H^{{ \mathrm class }}$ with $( id _P,\mathtt {environment},m)$. In all cases, the quantum communication register is not modified (i.e., the message in that register is forwarded).

Note the strong analogy to the corrupted parties (Page 10).

Thus, if we write $\pi$ quantum-UC emulates $\mathcal F$, we mean that $\pi$ quantum-UC emulates $\rho _\mathcal F$ where $\rho _\mathcal F$ consists of the functionality $\mathcal F$ and the dummy-parties corresponding to the parties in $\pi$. More precisely:

Definition 5

Let $\pi$ be a protocol and $\mathcal F$ be a functionality. We say that $\pi$ statistically/computationally quantum-UC emulates $\mathcal F$ if $\pi$ statistically/computationally quantum-UC emulates $\rho _\mathcal F$ where $\rho _\mathcal F:=\{\tilde{P}:P\in parties _\pi \}\cup \{\mathcal F\}$.

For more discussion of dummy-parties and functionalities, see [7].

Using the concept of an ideal functionality, we can specify a range of protocol tasks by simply defining the corresponding functionality. Below, we give the definitions of various functionalities. All these functionalities are classical; we therefore do not explicitly describe when the registers $\mathcal H^{{ \mathrm class }}$ and $\mathcal H^{{ \mathrm quant }}$ are measured/initialized but instead describe the functionality in terms of the messages sent and received.

Definition 6

(Commitment) Let A and B be two parties. The functionality $\mathcal F_\mathrm {COM}^{A\rightarrow B,\ell }$ behaves as follows: upon (the first) input $(\mathtt {commit},x)$ with $x\in \{0,1\}^{\ell (k)}$ from A, send $\mathtt {committed}$ to B. Upon input $\mathtt {open}$ from A send $(\mathtt {open},x)$ to B. All communication/input/output is classical.

We call A the sender and B the recipient.

Definition 7

(Oblivious transfer (OT)) Let A and B be two parties. The functionality $\mathcal F_\mathrm {OT}^{A\rightarrow B,\ell }$ behaves as follows: when receiving input $(s_0,s_1)$ from A with $s_0,s_1\in \{0,1\}^{\ell (k)}$ and $c\in \{0,1\}$ from B, send $s:=s_c$ to B. All communication/input/output is classical.

We call A the sender and B the recipient.

Definition 8

(Coin-toss) Let A and B be two parties. Let $\mathcal D$ be a distribution on $\{0,1\}^{*}$. The functionality $\mathcal F_\mathrm {CT}^{A, B,\mathcal D}$ behaves as follows: After having received $\mathtt {init}$ from both A and B, a value r is chosen according to $\mathcal D$, and then r is sent to A, B, and $\mathrm {Adv}$. All communication/input/output is classical.

We write $\mathcal F_\mathrm {CT}^{A, B,\ell }$ for the special case where $\mathcal D$ is the uniform distribution on $\{0,1\}^{\ell }$.

Definition 9

(CRS) Let A and B be two parties. Let $\mathcal D$ be a distribution on $\{0,1\}^{*}$. The functionality $\mathcal F_\mathrm {CRS}^{\mathcal D}$ (common reference string) behaves as follows: in its first activation, a bitstring r is chosen according to $\mathcal D$. Whenever receiving $\mathtt {getcrs}$ from a party P, the bitstring r is sent to P. All communication/input/output is classical.

Definition 10

(EPR functionality) Let A and B be two parties. The functionality $\mathcal F_\mathrm {EPR}^{A,B}$ behaves as follows: in its first activation, an EPR pair is chosen and stored in quantum registers $X_A,X_B$. When receiving $\mathtt {getepr}$ from $P\in \{A,B\}$ for the first time, $X_P$ is sent to P.

Definition 11

(Signature card) Let $\mathfrak S=(\mathrm {KG},\mathrm {Sign},\mathrm {Verify})$ be a signature scheme. Let A be a party. Then the functionality $\mathcal F_\mathrm {SC}^{\mathfrak S,A}$ (signature card for scheme $\mathfrak S$ with owner A) behaves as follows: upon the first activation, $\mathcal F_\mathrm {SC}^{\mathfrak S,A}$ chooses a verification/signing key pair $( pk , sk )$ using the key generation algorithm $\mathrm {KG}(1^\lambda )$. Upon a message $(\mathtt {getpk})$ from a party P or the adversary, it sends $pk$ to P or the adversary, respectively. Upon a message $(\mathtt {sign},m)$ from A $\mathcal F_\mathrm {SC}^{\mathfrak S,A}$ computes $\sigma \leftarrow \mathrm {Sign}( pk ,m)$ and sends $( pk ,\sigma )$ to A.

All communication/input/output is classical.

Definition 12

(Public key infrastructure) Let $\mathrm {KG}$ be a distribution on $\{0,1\}^{*}\times \{0,1\}^{*}$. The functionality $\mathcal F_\mathrm {PKI}^{A,\mathcal D}$ behaves as follows: in its first activation, a pair $( pk , sk )$ is chosen according to $\mathrm {KG}$. Whenever receiving $\mathtt {getkey}$ for a party $P\ne A$ or from $\mathrm {Adv}$, it sends $pk$ to P or $\mathrm {Adv}$, respectively. Whenever getting $\mathtt {getkey}$ from A, it sends $( pk , sk )$ to A.

Definition 13

(One-use authenticated channel) The functionality $\mathcal F_\mathrm {auth}^{A\rightarrow B}$ behaves as follows: when receiving the first message m from some party A, then m is sent to $\mathrm {Adv}$. Then, when receiving $\mathtt {deliver}$ from $\mathrm {Adv}$, m is sent to B. All communication/input/output is classical.

Definition 14

(One-use secure channel) The functionality $\mathcal F_\mathrm {secchan}^{A\rightarrow B}$ behaves as follows: when receiving the first message m from some party A, then $|m|$ is sent to $\mathrm {Adv}$. Then, when receiving $\mathtt {deliver}$ from $\mathrm {Adv}$, m is sent to B. All communication/input/output is classical.

Definition 15

(Key exchange) Let A and B be two parties. Let $\ell$ be an integer. The functionality $\mathcal F_\mathrm {KE}^{A,B,\ell }$ behaves as follows: when receiving $\mathtt {init}$ from A (for the first time), a uniformly random $K\in \{0,1\}^{\ell }$ is chosen (except if A or B is corrupted, in this case the adversary is asked for K). Then K is sent to A and B. All communication/input/output is classical.

The following definition allows to construct functionalities out of simpler ones. For example, a multi-use authenticated channel from A to B would be $(\mathcal F_\mathrm {auth}^{A\rightarrow B})^*$, and a bidirectional one would be $(\mathcal F_\mathrm {auth}^{A\rightarrow B})^*+(\mathcal F_\mathrm {auth}^{B\rightarrow A})^*$.

Definition 16

(Combined functionalities) Given functionalities $\mathcal F_1$ and $\mathcal F_2$, we define $\mathcal F_1+\mathcal F_2$ to be the functionality that internally simulates $\mathcal F_1$ and $\mathcal F_2$. Upon message (i, m) with $i=1,2$, m is sent to $\mathcal F_i$. When $\mathcal F_i$ sends m, the message is forwarded as (i, m).

Given a functionality $\mathcal F$, we defined ${\mathcal F^*}$ to be the functionality that internally simulates an instance $\mathcal F_ sid$ of $\mathcal F$ for every bitstring $sid$ (initialized upon first use). Upon message $( sid ,m)$, m is sent to $\mathcal F_ sid$. When $\mathcal F_ sid$ sends m, the message is forwarded as $( sid ,m)$.

3.3 Elementary Properties of UC-Security

Lemma 2

(Reflexivity, transitivity) Let $\pi$, $\rho$, and $\sigma$ be protocols. Then $\pi$ eqUC emulates $\pi$. If $\pi$ eqUC emulates $\rho$ and $\rho$ eqUC emulates $\sigma$, then $\pi$ eqUC emulates $\sigma$.

Proof

For any quantum-polynomial-time adversary $\mathrm {Adv}$ and any set C, with $\mathrm {Sim}:=\mathrm {Adv}$, we have that $\pi ^C\cup \{\mathrm {Adv},\mathcal Z\}$ and $\pi ^C\cup \{\mathrm {Sim},\mathcal Z\}$ are equal and hence perfectly trace-indistinguishable for all $\mathcal Z$. If $\mathrm {Adv}$ is quantum-polynomial-time, so is $\mathrm {Sim}=\mathrm {Adv}$. Thus, $\pi$ eqUC emulates $\pi$.

Assume that $\pi$ eqUC emulates $\rho$ and $\rho$ eqUC emulates $\sigma$. Fix a quantum-polynomial-time adversary $\mathrm {Adv}$ and a set C. Then there is a quantum-polynomial-time simulator $\mathrm {Sim}$ such that for all quantum-polynomial-time $\mathcal Z$, $\pi ^C\cup \{\mathrm {Adv},\mathcal Z\}$ and $\rho ^C\cup \{\mathrm {Sim},\mathcal Z\}$ are trace-indistinguishable. Furthermore, for the quantum-polynomial-time adversary $\mathrm {Adv}':=\mathrm {Sim}$, there is a quantum-polynomial-time simulator $\mathrm {Sim}'$ such that $\rho ^C\cup \{\mathrm {Sim},\mathcal Z\}=\rho ^C\cup \{\mathrm {Adv}',\mathcal Z\}$ and $\sigma ^C\cup \{\mathrm {Sim}',\mathcal Z\}$ are trace-indistinguishable for all quantum-polynomial-time $\mathcal Z$. From the triangle inequality of the trace distance, we have that trace-indistinguishability is transitive. Hence, $\pi ^C\cup \{\mathrm {Adv},\mathcal Z\}$ and $\sigma ^C\cup \{\mathrm {Sim}',\mathcal Z\}$ are indistinguishable for all quantum-polynomial-time $\mathcal Z$. Thus, $\pi$ eqUC emulates $\sigma$. $\square$

Dummy-Adversary In the definition of UC-security, we have three entities interacting with the protocol: the adversary, the simulator, and the environment. Both the adversary and the environment are all-quantified; hence, we would expect that they do, in some sense, work together. This intuition is backed by the following fact which was first noted by Canetti [7]: without loss of generality, we can assume an adversary that is completely controlled by the environment. This so-called dummy-adversary only forwards messages between the environment and the protocol. The actual attack is then executed by the environment.

Definition 17

(Dummy-adversary $\mathrm {Adv}_{ \mathrm dummy }$) When activated, the dummy-adversary $\mathrm {Adv}_{ \mathrm dummy }$ measures $\mathcal H^{{ \mathrm class }}$; call the outcome m. If m is of the form $(\mathtt {environment},\mathtt {adversary}, m')$, initialize $\mathcal H^{{ \mathrm class }}$ with $m'$. Otherwise initialize $\mathcal H^{{ \mathrm class }}$ with $(\mathtt {adversary},\mathtt {environment},m)$. In all cases, the quantum communication register is not modified (i.e., the message in that register is forwarded).

Note the strong analogy to the dummy-parties (Definition 4) and the corrupted parties (Page 10).

Lemma 3

(Completeness of the dummy-adversary) Assume that $\pi$ eqUC emulates $\rho$ with respect to the dummy-adversary (i.e., instead of quantifying over all adversaries $\mathrm {Adv}$, we fix $\mathrm {Adv}:=\mathrm {Adv}_{ \mathrm dummy }$). Then $\pi$ eqUC emulates $\rho$.

Proof

Assume that $\pi$ eqUC emulates $\rho$ with respect to the dummy-adversary. Fix a quantum-polynomial-time adversary $\mathrm {Adv}$. We have to show that there exists a quantum-polynomial-time simulator $\mathrm {Sim}$ such that for all quantum-polynomial-time environments $\mathcal Z$ we have that $\pi \cup \{\mathrm {Adv},\mathcal Z\}$ and $\rho \cup \{\mathrm {Sim},\mathcal Z\}$ are trace-indistinguishable.

For a given quantum-polynomial-time environment $\mathcal Z$, we construct a quantum-polynomial-time environment $\mathcal Z_\mathrm {Adv}$ that is supposed to interact with $\mathrm {Adv}_{ \mathrm dummy }$ and internally simulates $\mathcal Z$ and $\mathrm {Adv}$, and that routes all messages sent by the simulated $\mathrm {Adv}$ to $\pi$ through $\mathrm {Adv}_{ \mathrm dummy }$ and vice versa. Then $\pi \cup \{\mathrm {Adv},\mathcal Z\}$ and $\pi \cup \{\mathrm {Adv}_{ \mathrm dummy },\mathcal Z_\mathrm {Adv}\}$ are perfectly trace-indistinguishable. (Cf. networks (I) and (II) in Fig. 1.) Since $\pi$ eqUC emulates $\rho$ with respect to the dummy-adversary, we have that $\pi \cup \{\mathrm {Adv}_{ \mathrm dummy },\mathcal Z_\mathrm {Adv}\}$ and $\rho \cup \{\mathrm {Sim}',\mathcal Z_\mathrm {Adv}\}$ are indistinguishable for some quantum-polynomial-time $\mathrm {Sim}'$ and all $\mathcal Z$. (Cf. networks (II) and (III).) Since $\mathrm {Adv}_{ \mathrm dummy }$ is quantum-polynomial-time, so is $\mathrm {Sim}'$. We construct a quantum-polynomial-time machine $\mathrm {Sim}$ that internally simulates $\mathrm {Sim}'$ and $\mathrm {Adv}$ (network (IV)). Then $\rho \cup \{\mathrm {Sim}',\mathcal Z_\mathrm {Adv}\}$ and $\rho \cup \{\mathrm {Sim},\mathcal Z\}$ are perfectly trace-indistinguishable. Summarizing, $\pi \cup \{\mathrm {Adv},\mathcal Z\}$ and $\rho \cup \{\mathrm {Sim},\mathcal Z\}$ are trace-indistinguishable for all quantum-polynomial-time environments $\mathcal Z$. Thus, $\pi$ eqUC emulates $\rho$. $\square$

Fig. 1

Completeness of the dummy-adversary: proof steps

3.4 Universal Composition

For some protocol $\sigma$, and some protocol $\pi$, by $\sigma ^\pi$ we denote the protocol where $\sigma$ invokes (up to polynomially many) instances of $\pi$. That is, in $\sigma ^\pi$ the machines from $\sigma$ and from $\pi$ run together in one network, and the machines from $\sigma$ access the inputs and outputs of $\pi$. (That is, $\sigma$ plays the role of the environment from the point of view of $\pi$. In particular, $\mathcal Z$ then talks only to $\sigma$ and not to the subprotocol $\pi$ directly.) A typical situation would be that $\sigma ^\mathcal F$ is some protocol that makes use of some ideal functionality $\mathcal F$, say a commitment functionality, and then $\sigma ^\pi$ would be the protocol resulting from implementing that functionality with some protocol $\pi$, say a commitment protocol. (We say that $\sigma ^\mathcal F$ is a protocol in the $\mathcal F$-hybrid model.) One would hope that such an implementation results in a secure protocol $\sigma ^\pi$. That is, we hope that if $\pi$ eqUC emulates $\mathcal F$ and $\sigma ^\mathcal F$ eqUC emulates $\mathcal G$, then $\sigma ^\pi$ eqUC emulates $\mathcal G$. Fortunately, this is the case:

Theorem 1

(Universal Composition Theorem) Let $\pi$, $\rho$, and $\sigma$ be quantum-polynomial-time protocols. Assume that $\pi$ eqUC emulates $\rho$. Then $\sigma ^\pi$ eqUC emulates $\sigma ^\rho$.

If we additionally have that $\sigma ^\rho$ eqUC emulates $\mathcal G$, from the transitivity of eqUC emulation (Lemma 2), it immediately follows that $\sigma ^\pi$ eqUC emulates $\mathcal G$.

The composition guarantee given by Theorem 1 is often called universal composability. One should not confuse universal composability with UC-security. Although UC-security implies universal composability, it has been shown by Hofheinz and Unruh [19, 20, 33] that —in the classical setting at least—universal composability is a strictly weaker notion than UC-security.

Fig. 2

Networks occurring in the proof sketch of Theorem 1. Network (I) represents the real model, (II) the ideal model, and (III) the hybrid case. To avoid cluttering, in (III), the connections to $\pi _{i-1}$, $\mathrm {Sim}'_{i+1}$, and $\rho _{i+1}$ have been omitted

Proof of Theorem 1

Our goal is to prove that under the assumptions of Theorem 1, $\sigma ^\pi$ eqUC emulates $\sigma ^\rho$. Since $\sigma$ is quantum-polynomial-time, $\sigma$ invokes at most a polynomial number n of instances of its subprotocol $\pi$ or $\rho$. Since $\pi$ eqUC emulates $\rho$, there is a quantum-polynomial-time simulator $\mathrm {Sim}'$ such that for all quantum-polynomial-time environments $\mathcal Z$ we have that $\pi \cup \{\mathrm {Adv}_{ \mathrm dummy },\mathcal Z\}$ and $\rho \cup \{\mathrm {Sim}',\mathcal Z\}$ are trace-indistinguishable. In the following, we call $\mathrm {Sim}'$ the dummy-simulator.

Let a quantum-polynomial-time adversary $\mathrm {Adv}$ be given (that is supposed to attack $\sigma ^\pi$). We construct a simulator $\mathrm {Sim}$ that internally simulates the adversary $\mathrm {Adv}$ and n instances $\mathrm {Sim}'_1,\dots ,\mathrm {Sim}'_n$ of the dummy-simulator $\mathrm {Sim}'$. The simulated adversary $\mathrm {Adv}$ is connected to the environment and to the protocol $\sigma$, but all messages between $\mathrm {Adv}$ and the i-th instance $\pi _i$ of $\pi$ are routed through the dummy-simulator-instance $\mathrm {Sim}'_i$ (which is then supposed to transform these messages into a form suitable for instances of $\rho$). The simulator $\mathrm {Sim}$ is depicted by the dashed box in network (II) in Fig. 2.

We have to show that for any quantum-polynomial-time environment $\mathcal Z$ we have that $\sigma ^\pi \cup \{\mathrm {Adv},\mathcal Z\}$ and $\sigma ^\rho \cup \{\mathrm {Sim},\mathcal Z\}$ are trace-indistinguishable (networks (I) and (II) in Fig. 2).

For this, we construct a hybrid environment $\mathcal Z_{\sigma ,i}$. ($\mathcal Z_{\sigma ,i}$ is depicted as the dashed box in network (III) in Fig. 2.) This environment internally simulates the machines $\mathcal Z$, $\mathrm {Adv}$, the protocol $\sigma$, instances $\pi _1,\dots ,\pi _{i-1}$ of the real protocol $\pi$, and instances $\mathrm {Sim}'_{i+1},\dots ,\mathrm {Sim}'_n$ and $\rho _{i+1},\dots ,\rho _n$ of the dummy-simulator $\mathrm {Sim}'$ and the ideal protocol $\rho$, respectively. The communication between $\mathcal Z$, $\mathrm {Adv}$, and $\sigma$ is directly forwarded by $\mathcal Z_{\sigma ,i}$. Communication between $\mathrm {Adv}$ and the j-th protocol instance is forwarded as follows: if $j<i$, the communication is simply forwarded to $\pi _j$. If $j>i$, the communication is routed through the corresponding dummy-simulator $\mathrm {Sim}'_j$ (which is then supposed to transform these messages into a form suitable for $\rho _j$). And finally, if $j=i$, the communication is passed to the adversary/simulator outside of $\mathcal Z_{\sigma ,i}$. Communication between $\sigma$ and the instances of $\pi$ or $\rho$ is directly forwarded.

We will now show that there is a negligible function $\mu$ such that ${\mathrm {TD}}(\mathrm {QExec}_{\pi \cup \{\mathrm {Adv}_{ \mathrm dummy },\mathcal Z_{\sigma ,i}\}}(\eta ,z),\mathrm {QExec}_{\rho \cup \{\mathrm {Sim}',\mathcal Z_{\sigma ,i}\}}(\eta ,z))\le \mu (k)$ for any security parameter $\eta$ and any $i=1,\dots ,n$. For this, we construct an environment $\mathcal Z_\sigma$ which expects as its initial input a pair (i, z), and then runs $\mathcal Z_{\sigma ,i}$ with input z. Since $\pi \cup \{\mathrm {Adv}_{ \mathrm dummy },\mathcal Z\}$ and $\rho \cup \{\mathrm {Sim}',\mathcal Z\}$ are trace-indistinguishable for all quantum-polynomial-time environments $\mathcal Z$, there exists a negligible function $\mu$ such that the trace distance of $\mathrm {QExec}_{\pi \cup \{\mathrm {Adv}_{ \mathrm dummy },\mathcal Z_{\sigma ,i}\}}(\eta ,z) = \mathrm {QExec}_{\pi \cup \{\mathrm {Adv}_{ \mathrm dummy },\mathcal Z_{\sigma }\}}(\eta ,(i,z))$ and $\mathrm {QExec}_{\rho \cup \{\mathrm {Sim}',\mathcal Z_{\sigma ,i}\}}(\eta ,z) =\mathrm {QExec}_{\rho \cup \{\mathrm {Sim}',\mathcal Z_{\sigma }\}}(\eta ,(i,z))$ is bounded by $\mu (k)$ for all i, k, z.

The game $\mathrm {QExec}_{\pi \cup \{\mathrm {Adv}_{ \mathrm dummy },\mathcal Z_{\sigma ,i}\}}(\eta ,z)$ is depicted as network (III) in Fig. 2 (except that we wrote $\pi _i$ instead of $\pi$). Observe that $\mathrm {QExec}_{\rho \cup \{\mathrm {Sim}',\mathcal Z_{\sigma ,i+1}\}}(\eta ,z)$ (note the changed index $i+1$) contains the same machines as $\mathrm {QExec}_{\pi \cup \{\mathrm {Adv}_{ \mathrm dummy },\mathcal Z_{\sigma ,i}\}}(\eta ,z)$ (when unfolding the simulation performed by $\mathcal Z_{\sigma ,i}$ into individual machines) except for the difference that the communication with the i-th instance of $\pi$ is routed through the dummy-adversary $\mathrm {Adv}_{ \mathrm dummy }$. However, the latter just forwards messages, so $\pi \cup \{\mathrm {Adv}_{ \mathrm dummy },\mathcal Z_{\sigma ,i}\}$ and $\rho \cup \{\mathrm {Sim}',\mathcal Z_{\sigma ,i+1}\}$ are perfectly trace-indistinguishable.

Using the triangle inequality for the trace distance, it follows that ${\mathrm {TD}}(\mathrm {QExec}_{\pi \cup \{\mathrm {Adv}_{ \mathrm dummy },\mathcal Z_{\sigma ,n}\}}(\eta ,z), \mathrm {QExec}_{\rho \cup \{\mathrm {Sim}',\mathcal Z_{\sigma ,1}\}}(\eta ,z))$ is bounded by $n\cdot \mu (k)$ which is negligible. Moreover, $\mathrm {QExec}_{\pi \cup \{\mathrm {Adv}_{ \mathrm dummy },\mathcal Z_{\sigma ,n}\}}(\eta ,z)$ and $\mathrm {QExec}_{\sigma ^\pi \cup \{\mathrm {Adv},\mathcal Z\}}(\eta ,z)$ describe the same game (up to unfolding of simulated submachines and up to one instance of the dummy-adversary). Similarly, $\mathrm {QExec}_{\rho \cup \{\mathrm {Sim}',\mathcal Z_{\sigma ,1}\}}(\eta ,z)$ and $\mathrm {QExec}_{\sigma ^\rho \cup \{\mathrm {Sim},\mathcal Z\}}(\eta ,z)$ describe the same game (up to unfolding of simulated submachines). Thus, ${\mathrm {TD}}(\mathrm {QExec}_{\sigma ^\pi \cup \{\mathrm {Adv},\mathcal Z\}}(\eta ,z), \mathrm {QExec}_{\sigma ^\rho \cup \{\mathrm {Sim},\mathcal Z\}}(\eta ,z))$ is negligible and thus $\sigma ^\pi \cup \{\mathrm {Adv},\mathcal Z\}$ and $\sigma ^\rho \cup \{\mathrm {Sim},\mathcal Z\}$ are trace-indistinguishable. Furthermore, since $\mathrm {Adv}$ and $\mathrm {Sim}'$ are quantum-polynomial-time, so is $\mathrm {Sim}$.

Since this holds for all $\mathcal Z$, and the construction of $\mathrm {Sim}$ does not depend on $\mathcal Z$, we have that $\sigma ^\pi$ eqUC emulates $\sigma ^\rho$. $\square$

4 Impossibilities

In Sect. 6, we show that by using signature cards and a quantum channel, we can construct general everlastingly secure MPC protocols. The question arises whether both signature cards and quantum channels are needed. We answer this question positively by showing that (a) in the classical setting, most typical trusted setup (including signature cards) is not sufficient to implement everlasting OT and that (b) in the quantum setting, typical trusted setup such as a CRS is not sufficient to implement everlasting OT. The impossibilities even apply if we do not try to achieve UC-security but only to implement a stand-alone OT.

4.1 Classical Impossibilities

We first give a short overview of our technique. The basic observation underlying our impossibility result is that a protocol that is everlastingly secure is also secure against unlimited passive adversaries. This is due to the fact that a passive adversary follows the protocol during the protocol execution (and is thus polynomial-time) and only after the protocol execution performs an unlimited computation. Thus, if an unlimited passive adversary could break the protocol, the protocol would not be everlastingly secure either.

We call a functionality $\mathcal F$ passively realizable if there is a protocol that realizes $\mathcal F$ with respect to unlimited passive adversaries. We show that the following functionalities are passively realizable: the coin-toss $\mathcal F_\mathrm {CT}$, the common reference string $\mathcal F_\mathrm {CRS}$, the public key infrastructure $\mathcal F_\mathrm {PKI}$, the commitment $\mathcal F_\mathrm {COM}$, and the signature card $\mathcal F_\mathrm {SC}$.

Assume now an everlastingly secure OT protocol $\pi$ that uses a passively realizable functionality $\mathcal F$. Then $\pi$ is also secure against passive unlimited adversaries. Let $\rho$ be the protocol that realizes $\mathcal F$ (passively). Then $\pi '$, resulting from replacing $\mathcal F$ by $\rho$, will still be an OT secure against passive unlimited adversaries. (Here, of course, we have to be careful with our definition of passively realizing a functionality—the notion needs to compose such that $\pi '$ is still secure.) But $\pi '$ does not use any functionality, and we know that no OT protocol in the bare model can be secure against unlimited passive adversaries.

Concluding, we get:

Theorem 2

(Simplified, see Corollary 1) There is no everlastingly secure OT protocol which only uses arbitrarily many instances of $\mathcal F_\mathrm {CT}$ (coin-toss), $\mathcal F_\mathrm {CRS}$ (common reference string), $\mathcal F_\mathrm {COM}$ (commitment), $\mathcal F_\mathrm {PKI}$ (public key infrastructure), and $\mathcal F_\mathrm {SC}$ (signature cards).

We now present the details of the above argumentation:

For a set C of machine identities and a network $\mathbf N$ of classical machines, let $\mathrm {Exec}^C_\mathbf N(\eta ,z)$ denote the random variable describing the (classical) states of the machines in $C\cup \{\mathtt {environment}\}$ after the execution of $\mathbf N$.

A non-erasing dummy-party is defined like a dummy-party, except that it stores all messages it gets and sends in its state. (This only makes sense in a classical setting, of course.) A non-erasing machine is a machine that stores all messages it sends and receives and all its intermediate states in its state. For a functionality $\mathcal F$, we write $\rho _\mathcal F':=\{\tilde{P}':P\in parties _\pi \}\cup \{\mathcal F\}$ where $\tilde{P}'$ denotes the non-erasing dummy-party for P. (Cf. Definition 5.) We call a protocol non-erasing if it consists only of non-erasing machines. We call a protocol $\pi$ functionality-free if $parties _\pi = ids _\pi$ (i.e., all machines are parties).

We first define the notion of passively realizable functionalities. Roughly, a functionality is passively realizable if there is a protocol that implements this functionality with respect to passive adversaries. We will show that any such passively realizable functionality is essentially useless for implementing everlastingly secure OT in a classical setting.

Definition 18

Fix classical protocols $\pi$ and $\rho$ with $parties _\pi = parties _\rho$. We say $\pi$ passively emulates  $\rho$ iff:

• For any (possibly unbounded) environment $\mathcal Z$, $\mathrm {Exec}^{\varnothing }_{\pi \cup \{\mathcal Z\}}(\eta ,z)$ and $\mathrm {Exec}^{\varnothing }_{\rho \cup \{\mathcal Z\}}(\eta ,z)$ are statistically indistinguishable.

• There exists a probabilistic function $S_A$ such that for any (possibly unbounded) environment $\mathcal Z$, the random variables $\mathrm {Exec}^{A}_{\pi \cup \{\mathcal Z\}}(\eta ,z)$ and $\bar{S}_A(\mathrm {Exec}^{A}_{\rho \cup \{\mathcal Z\}}(\eta ,z))$ are statistically indistinguishable. Here $\bar{S}_A:= id \times S_A$ denotes the function that is the identity on $\mathcal Z$’s state and applies $S_A$ to A’s state.

• The same with B instead of A.

We call a functionality $\mathcal F$ passively realizable if there is a (possibly unbounded) non-erasing functionality-free protocol $\pi$ such that $\pi$ passively emulates $\rho _\mathcal F'$.

Lemma 4

The following functionalities are passively realizable: $\mathcal F_\mathrm {CT}$ (coin-toss), $\mathcal F_\mathrm {CRS}$ (common reference string), $\mathcal F_\mathrm {COM}$ (commitment), $\mathcal F_\mathrm {PKI}$ (public key infrastructure), $\mathcal F_\mathrm {SC}$ (signature cards).

Proof

For each of the functionalities listed in the lemma, we need to give a protocol satisfying Definition 18.

For $\mathcal F_\mathrm {CT}$, the protocol $\pi _{\mathcal F_\mathrm {CT}}$ consists of Alice choosing the random value r and sending it to Bob. The function $S_A$ takes the state of the Alice-dummy-party which contains the coins r and produces the state that Alice would have after choosing r at random and sending it to Bob. The function $S_B$ takes the state of the Bob-dummy-party which contains the coins r and produces the state that Bob would have after receiving r from Alice.

For $\mathcal F_\mathrm {CRS}$, the situation is analogous to $\mathcal F_\mathrm {CT}$.

For $\mathcal F_\mathrm {COM}$, the protocol $\pi _{\mathcal F_\mathrm {COM}}$ is the following: upon input $(\mathtt {commit},x)$, Alice sends $\mathtt {committed}$ to Bob. Upon a later input $\mathtt {open}$, Alice sends $(\mathtt {open},x)$ to B. When receiving $\mathtt {committed}$ or $(\mathtt {open},x)$ from Alice, Bob outputs $\mathtt {committed}$ or $(\mathtt {open},x)$, respectively, to the environment. The function $S_A$ replaces the outgoing messages $\mathtt {committed}$ and $(\mathtt {open},x)$ in Alice’s state by $(\mathtt {commit},x)$ and $\mathtt {open}$, respectively. The function $S_B$ does not change the messages received/sent by Bob.

For $\mathcal F_\mathrm {PKI}^{\mathrm {KG},A}$, the protocol $\pi _{\mathcal F_\mathrm {PKI}}$ is the following: A selects $( pk , sk )$ according to $\mathrm {KG}$. When a party P requests the public key, A sends the public key to that party. In addition to $pk , sk$ which are obtained from $\mathcal F_\mathrm {PKI}$, the function $S_A$ needs to compute the randomness used by $\mathrm {KG}$ to compute $( pk , sk )$. This randomness is sampled uniformly from all possible values that lead to $( pk , sk )$.

For $\mathcal F_\mathrm {SC}^{\mathfrak S,A}$, the protocol $\pi _{\mathcal F_\mathrm {PKI}}$ is the follows. A selects $( pk , sk )$ according to the key generation algorithm of $\mathfrak S$ and produces all signatures on its own. When another party requests the public key, A provides it. As with $\mathcal F_\mathrm {PKI}$, $S_A$ needs to produce the randomness that was used to produce the keys and the signatures, this randomness is sampled randomly from those randomnesses that lead to the keys and signatures that were produced by $\mathcal F_\mathrm {SC}$. $\square$

Definition 19

(Minimally secure OT) We call a two-party protocol $\pi$ a minimally secure OT if the following properties hold:

• Correctness: If Alice and Bob are honest, and Alice has input $m_0,m_1\in \{0,1\}$, and Bob has input $c\in \{0,1\}$, then Bob gets output $m_c$ with overwhelming probability.

• Alice-security: For any adversary $B^*$ we have that $B^*$ cannot guess both Alice’s inputs with overwhelming probability. More precisely, let Alice get uniformly distributed inputs $m_0,m_1\in \{0,1\}$ and $c\in \{0,1\}$. Let the output of $B^*$ be $(m_0^*,m_1^*)$ after interacting with Alice. Then $\Pr [(m_0^*,m_1^*)=(m_0,m_1)]$ is not overwhelming.

• Bob-security: For any adversary $A^*$ we have that $A^*$ cannot distinguish between Bob with input 0 and Bob with input 1. More precisely, let Alice get uniformly distributed inputs $m_0,m_1\in \{0,1\}$ and $c\in \{0,1\}$. Let $P_c$ be the probability that $A^*$ outputs 1 when interacting with Bob. Then $|P_0-P_1|$ is negligible in the security parameter.

We distinguish between minimally secure everlasting OT in which we only consider adversaries $A^*$ and $B^*$ that are computationally bounded during the protocol execution and unlimited afterward, and minimally secure passive OT in which the adversaries $A^*$ and $B^*$ are unbounded but passive (semi-honest).⁹

Lemma 5

There is no functionality-free minimally secure passive OT protocol.

The fact is well known, but we are not aware of a reference. Lemma 5 does follow directly from the quantum case (Lemma 9 below), though.

Lemma 6

If $\mathcal F$ and $\mathcal G$ are passively realizable then $\mathcal F+\mathcal G$ and ${\mathcal F^*}$ are passively realizable.

Proof

Let $\pi _\mathcal F$ and $\pi _\mathcal G$ be the non-erasing functionality-free protocols that passively emulate $\rho '_{\mathcal F}$ and $\rho '_{\mathcal G}$, respectively. It is easy to see that then $\pi _\mathcal F+\pi _\mathcal G$ (the non-erasing functionality-free protocol constructed by combining each party of $\pi _\mathcal F$ with the corresponding party of $\pi _\mathcal G$) passively emulates $\rho '_{\mathcal F+\mathcal G}$, and similarly ${\pi _\mathcal F^*}$ passively emulates $\rho '_{{\mathcal F^*}}$. $\square$

Lemma 7

There is no minimally secure passive OT protocol which only uses passively realizable functionalities (even if we allow it to use several different passively realizable functionalities and arbitrarily many instances of each).

Proof

By Lemma 6, it is sufficient to show that there is no minimally secure passive OT protocol $\rho$ which only uses a single instance of a passively realizable functionality $\mathcal F$.

Fix a protocol $\rho$ using a single instance of a passively realizable functionality $\mathcal F$. We will show that $\rho$ is not a minimally secure passive OT protocol.

Let $\pi _\mathcal F$ be the non-erasing functionality-free protocol that passively emulates $\mathcal F$ by Definition 18. Let $\sigma$ be the protocol resulting from $\rho$ by replacing invocations of $\mathcal F$ by invocations of the subprotocol $\pi _\mathcal F$. Then also $\sigma$ is non-erasing and functionality-free. Then by Lemma 5, $\sigma$ is not a minimally secure passive OT protocol.

Thus, one of the three conditions from Definition 19 is not satisfied.

Assume that the Alice-security is not fulfilled. That is, there is a passive adversary $B^*$ that guesses Alice’s inputs with overwhelming probability. More formally: let $\mathcal Z$ be the environment that chooses uniformly random $m_0,m_1,c\in \{0,1\}$ and provides these values to Alice and Bob and that keeps just $(m_0,m_1)$ as its final state. Then there is a probabilistic function f such that

$$\begin{aligned} \text {for } ( st _\mathcal Z, st _B)\leftarrow (\mathrm {Exec}^B_{\sigma \cup \{\mathcal Z\}}(\eta ,z)) \text { we have } st _\mathcal Z=f( st _B) \text { with overwhelming probability.} \end{aligned}$$

(1)

Now, since $\pi _\mathcal F$ passively emulates $\mathcal F$, and since we can consider the machines in $\sigma$ that are not part of the subprotocol $\pi _\mathcal F$ as part of a new environment $\mathcal Z'$ (simulating the original $\mathcal Z$ and those machines), we have that there is a function $S_B$ such that $\mathrm {Exec}^B_{\sigma \cup \{\mathcal Z\}}$ and $\bar{S}_B(\mathrm {Exec}^B_{\rho \cup \{\mathcal Z\}})$ are statistically indistinguishable. (Here $\bar{S}_B$ is defined as in Definition 18.)

With (1), we get that for $( st _\mathcal Z, st _B)\leftarrow (\mathrm {Exec}^B_{\rho \cup \{\mathcal Z\}}(\eta ,z))$ we have $st _\mathcal Z=f(S_B( st _B))$ with overwhelming probability.

This, however, implies that $\rho$ is not a minimally secure passive OT protocol (because it breaks the Alice-security of $\rho$).

If we assume that the Bob-security of $\sigma$ is not fulfilled, we analogously get that the Bob-security of $\rho$ is not fulfilled. (By corrupting Alice instead of Bob.) And finally if the correctness of $\sigma$ is not fulfilled, the correctness of $\rho$ is not fulfilled.

Since $\sigma$ is not minimally secure, it follows that one of the three properties is not fulfilled, and thus $\rho$ is not minimally secure, either. $\square$

Theorem 3

There is no polynomial-time minimally secure everlasting OT protocol which only uses passively realizable functionalities (even if we allow it to use several different passively realizable functionalities and arbitrarily many instances of each).

Proof

For a polynomial-time protocol, any passive adversary is computationally bounded during the protocol execution (since he only has to execute the protocol). Thus, the adversaries considered in minimally secure everlasting OT are a superset of those considered in minimally secure passive OT. $\square$

Corollary 1

There is no polynomial-time minimally secure everlasting OT protocol which only uses arbitrarily many instances of $\mathcal F_\mathrm {CT}$ (coin-toss), $\mathcal F_\mathrm {CRS}$ (common reference string), $\mathcal F_\mathrm {COM}$ (commitment), $\mathcal F_\mathrm {PKI}$ (public key infrastructure), and $\mathcal F_\mathrm {SC}$ (signature cards).

Proof

Immediate from Theorem 3 and Lemma 4. $\square$

4.2 Quantum Impossibilities

The impossibility in the quantum case follows similar lines. However, the classical notion of passive adversaries does not make sense in the quantum case. (A passive adversary copies all data, this is not possible in the quantum case.) To solve this issue, we consider only protocols that perform no measurements (unitary protocols). Any protocol can be transformed into such a protocol at the expense of additional quantum memory. We call a functionality $\mathcal F$ quantum-passively realizable if there is a unitary protocol $\pi$ that realizes $\mathcal F$ with respect to quantum-passive unlimited adversaries (meaning adversaries that follow the protocol exactly and do not even copy information). Notice that the requirement that $\pi$ has to be unitary has the effect that the protocol cannot just throw away information.¹⁰ Thus, an adversary that is quantum-passive will still have some information left over after the protocol execution. The following functionalities turn out to be quantum-passively realizable: coin-toss $\mathcal F_\mathrm {CT}$, predistributed EPR pairs $\mathcal F_\mathrm {EPR}$, public key infrastructure $\mathcal F_\mathrm {PKI}$ (assuming the secret key is uniquely determined by the public key). However, signature cards and commitments are not! (The reason being that signature cards and commitments do not allow to commit/sign superpositions of messages and thus enforce measurements. This cannot be realized with a unitary protocol.)

Then we can proceed as in the classical case: assume an everlasting quantum OT protocol $\pi$ using a quantum-passively realizable functionality $\mathcal F$. This protocol is also secure against unlimited quantum-passive adversaries (in the above sense). By replacing $\mathcal F$ by the protocol $\rho$ that realizes $\mathcal F$, we get a quantum OT protocol $\pi '$ not using any functionality that is secure against unlimited quantum-passive adversaries. But Lo [24] shows that such protocols do not exist. Thus we get:

Theorem 4

(Simplified, see Corollary 2) There is no quantum-polynomial-time everlastingly secure OT protocol which only uses arbitrarily many instances of $\mathcal F_\mathrm {CT}$ (coin-toss), $\mathcal F_\mathrm {CRS}$ (common reference string), $\mathcal F_\mathrm {EPR}$ (predistributed EPR pair), $\mathcal F_\mathrm {PKI}$ (public key infrastructure; assuming that the secret key is uniquely determined by the public key).

We now present the details of the above argumentation:

For a set C of machine identities and a network $\mathbf N$ of machines, let $\mathrm {QExec}^C_\mathbf N(\eta ,z)$ denote the joint state of the machines in $C\cup \{\mathtt {environment}\}$ after the execution of $\mathbf N$.

A unitary machine is a machine whose state transition operator is unitary. We call a protocol unitary if it consists only of unitary machines.

In order to get a result analogous to the classical impossibility result from Theorem 3, we need a definition analogous to the classical notion of passive realizability. The classical notion of passive (semi-honest) behavior does not make sense in the quantum setting, a machine cannot store copies of its state in every step of the interaction. Instead, we opt for the next best thing: we require machines to be unitary. This implies that they will not be able to destroy information (though they can lose some information if the protocol requires them to send it to some other machine).

Definition 20

Fix quantum protocols $\pi$ and $\rho$ with $parties _\pi = parties _\rho$. We say $\pi$ quantum-passively emulates $\rho$ iff:

• For any (possibly unbounded) environment $\mathcal Z$, $\mathrm {QExec}^{\varnothing }_{\pi \cup \{\mathcal Z\}}(\eta ,z)$ and $\mathrm {QExec}^{\varnothing }_{\rho \cup \{\mathcal Z\}}(\eta ,z)$ are trace-indistinguishable.

• There exists a superoperator $\mathcal E_A$ such that for any (possibly unbounded) environment $\mathcal Z$, the random variables $\mathrm {QExec}^{A}_{\pi \cup \{\mathcal Z\}}(\eta ,z)$ and $\bar{\mathcal E}_A(\mathrm {QExec}^{A}_{\rho \cup \{\mathcal Z\}}(\eta ,z))$ are trace-indistinguishable. Here $\bar{\mathcal E}_A:= id \otimes \mathcal E_A$ denotes the superoperator that is the identity on $\mathcal Z$’s state and applies $\mathcal E_A$ to A’s state.

• The same with B instead of A.

We call a machine $\tilde{P}^u$ a unitary dummy-party for $\mathcal F$ and P if $\tilde{P}^u$ is unitary and $\{\tilde{P}^u,\mathcal F\}$ is indistinguishable from $\{\tilde{P},\mathcal F\}$ where $\tilde{P}$ is the dummy-party for $\mathcal F$ and P.

We call a functionality $\mathcal F$ quantum-passively realizable if there is a (possibly unbounded) unitary functionality-free protocol $\pi$ and for each $P\in parties _\pi$ there exists a unitary dummy-party $\tilde{P}^u$ for $\mathcal F$ and P such that $\pi$ quantum-passively emulates $\{\mathcal F,\tilde{P}^u\ (P\in parties _\pi )\}$.

Lemma 8

The following functionalities are quantum-passively realizable: $\mathcal F_\mathrm {CT}$ (coin-toss), $\mathcal F_\mathrm {CRS}$ (common reference string), $\mathcal F_\mathrm {EPR}$ (predistributed EPR pair), $\mathcal F_\mathrm {PKI}$ (public key infrastructure; assuming that the secret key is uniquely determined by the public key).

Notice that $\mathcal F_\mathrm {COM}$ and $\mathcal F_\mathrm {SC}$ are not listed here. These are not quantum-passively realizable, even though they are passively realizable. In fact, as we show below, quantum-passively realizable functionalities are useless for implementing everlastingly secure OT, but commitment is sufficient for constructing even statistically secure OT protocols [4] (see [34] for a proof in the quantum-UC-setting). And in Sect. 6 we show that with signature cards we can construct everlastingly secure OTs.

Proof

For each of the functionalities $\mathcal F$ listed in the lemma, we need to give a protocol $\pi _\mathcal F$ satisfying Definition 20.

For $\mathcal F_\mathrm {EPR}$, the protocol $\pi _{\mathcal F_\mathrm {EPR}}$ consists of Alice producing an EPR pair and sending the second half of it to Bob (over a secure channel). Since for producing an EPR pair, no ancillae or measurements are needed, the states of Alice and Bob after outputting their halves of the EPR pairs are empty. Thus, the superoperators $\mathcal E_A$ and $\mathcal E_B$ (as in Definition 20) can be chosen to be the identity, and the unitary dummy-parties $\tilde{A}^u$ and $\tilde{B}^u$ to be machines that just forward their outputs (without measuring).

Fig. 3

Circuit for computing a CRS

For $\mathcal F_\mathrm {CRS}^{\mathcal D}$, let f be a function and $\ell$ be an integer such that f(r) is distributed according to $\mathcal D$ for a uniformly chosen $r\in \{0,1\}^{\ell }$. Let k be the length needed for encoding outputs of $\mathcal D$. Alice evaluates the quantum circuit described in Fig. 3. Then she outputs the first register as CRS, keeps the second, and sends the third and fourth register to Bob. Bob outputs the fourth register as CRS and keeps the third. We use dummy-parties $\tilde{A}^u$ and $\tilde{B}^u$ that use CNOT to “copy” the CRS. More precisely, before forwarding the CRS from $\mathcal F_\mathrm {CRS}$ to $\mathcal Z$, $\tilde{A}^u$ applies $U:{\left| {x,y}\right\rangle }\mapsto {\left| {x,x\oplus y}\right\rangle }$ to the CRS and a fresh ${\left| {0^k}\right\rangle }$-initialized quantum register.

Consider the case that Alice is corrupted. In this case, in the ideal model, the joint state consisting of Alice’s and Bob’s output (the CRS) and Alice’s state is:

$$\begin{aligned} \rho ^I=\sum _d\mathcal D(d)\cdot {\left| {d}\right\rangle }{\left\langle {d}\right| }\otimes {\left| {d}\right\rangle }{\left\langle {d}\right| }\otimes {\left| {d}\right\rangle }{\left\langle {d}\right| } \end{aligned}$$

where $\mathcal D(d)$ denotes the probability that $\mathcal D$ assigns to d. In the real model, that state is

$$\begin{aligned} \rho ^R = \sum _r 2^{-\ell }{\left| {f(r)}\right\rangle }{\left\langle {f(r)}\right| }\otimes {\left| {f(r)}\right\rangle }{\left\langle {f(r)}\right| }\otimes {\left| {r}\right\rangle }{\left\langle {r}\right| }. \end{aligned}$$

We need to find a superoperator $\mathcal E_A$ such that $( id \otimes id \otimes \mathcal E_A)\rho ^I=\rho ^R$. This is satisfied by any superoperator $\mathcal E_A$ that maps ${\left| {d}\right\rangle }{\left\langle {d}\right| }$ to $\sum _{r:f(r)=d}\frac{1}{|\{r:f(r)=d\}|}{\left| {r}\right\rangle }{\left\langle {r}\right| }$. This shows that $\pi _{\mathcal F_\mathrm {CRS}}$ quantum-passively emulates $\mathcal F_\mathrm {CRS}$ in the case of corrupted Alice. The case of corrupted Bob is analogous.

For $\mathcal F_\mathrm {CT}$, the proof is analogous to that for $\mathcal F_\mathrm {CRS}$.

For $\mathcal F_\mathrm {PKI}^{\mathrm {KG},A}$, the proof is analogous to that for $\mathcal F_\mathrm {CRS}$, except that we use two different functions $f_A,f_B$ for computing Alice’s and Bob’s output. $f_A(r)$ is distributed like the output $( pk , sk )$ of the key generation, $f_B(r)$ is the first component of $f_A(r)$. Since we assume that the secret key $sk$ can be computed (inefficiently) from the public key $pk$, we have that $f_A(r)$ and $f_B(r)$ contain the same information about r. $\square$

Definition 21

(Minimally secure quantum OT) We introduce two further variants of the definition of minimally secure OT (Definition 19): in minimally secure quantum everlasting OT, we consider quantum adversaries $A^*$ and $B^*$ that are computationally bounded during the protocol execution and unlimited afterward. In minimally secure quantum-passive OT the quantum adversaries $A^*$ and $B^*$ are unbounded but quantum-passive, more precisely, $A^*$ and $B^*$ behave like Alice and Bob, respectively, during the protocol execution, and may apply an arbitrary measurement to their state after the protocol execution for determining their output.

Lemma 9

There is no functionality-free minimally secure quantum-passive OT protocol.

This was shown in [24] (although no formal statement of the actual result was given).

Lemma 10

If $\mathcal F$ and $\mathcal G$ are quantum-passively realizable then $\mathcal F+\mathcal G$ and ${\mathcal F^*}$ are quantum-passively realizable.

Proof

Let $\pi _\mathcal F$ and $\pi _\mathcal G$ be the unitary functionality-free protocols that quantum-passively emulate $\rho _{\mathcal F}$ and $\rho _{\mathcal G}$, respectively. It is easy to see that then $\pi _\mathcal F+\pi _\mathcal G$ (the unitary functionality-free protocol constructed by combining each party of $\pi _\mathcal F$ with the corresponding party of $\pi _\mathcal G$) quantum-passively emulates $\rho _{\mathcal F+\mathcal G}$, and similarly ${\pi _\mathcal F^*}$ quantum-passively emulates $\rho _{{\mathcal F^*}}$. $\square$

Lemma 11

There is no minimally secure quantum-passive OT protocol which only uses quantum-passively realizable functionalities (even if we allow it to use several different quantum-passively realizable functionalities and arbitrarily many instances of each).

Proof

By Lemma 10, it is sufficient to show that there is no minimally secure quantum-passive OT protocol $\rho$ which only uses a single instance of a quantum-passively realizable functionality $\mathcal F$.

Fix a protocol $\rho$ using a single instance of a quantum-passively realizable functionality $\mathcal F$. We will show that $\rho$ is not a minimally secure quantum-passive OT protocol.

Let $\pi _\mathcal F$ be the unitary functionality-free protocol that quantum-passively emulates $\mathcal F$ by Definition 20. Let $\sigma$ be the protocol resulting from $\rho$ by replacing invocations of $\mathcal F$ by invocations of the subprotocol $\pi _\mathcal F$. Then also $\sigma$ is unitary and functionality-free. Then by Lemma 9, $\sigma$ is not a minimally secure quantum-passive OT protocol.

Thus, one of the three conditions from Definition 19 is not satisfied.

Assume that the Alice-security is not fulfilled. That is, there is a quantum-passive adversary $B^*$ that guesses Alice’s inputs with overwhelming probability. More formally: let $\mathcal Z$ be the environment that chooses uniformly random $m_0,m_1,c\in \{0,1\}$ and provides these values to Alice and Bob and that keeps just $(m_0,m_1)$ as its final state. Then there is a measurement $\mathcal M$ such that

$$\begin{aligned} \text {for } ( st _\mathcal Z,\rho _B)\leftarrow (\mathrm {QExec}^B_{\sigma \cup \{\mathcal Z\}}(\eta ,z)) \text { we have } st _\mathcal Z=\mathcal M(\rho _B) \text { with overwhelming probability.} \end{aligned}$$

(2)

Note that here we can treat $\mathcal Z$’s output as a classical value $st _\mathcal Z$ because it consists only of the values $m_0,m_1$. $\mathcal M(\rho _B)$ denotes the measurement outcome after applying $\mathcal M$ to Bob’s output state $\rho _B$.

Now, since $\pi _\mathcal F$ quantum-passively emulates $\mathcal F$, and since we can consider the machines in $\sigma$ that are not part of the subprotocol $\pi _\mathcal F$ as part of a new environment $\mathcal Z'$ (simulating the original $\mathcal Z$ and those machines), we have that there is a superoperator $\mathcal E_B$ such that $\mathrm {QExec}^B_{\sigma \cup \{\mathcal Z\}}$ and $\bar{\mathcal E}_B(\mathrm {QExec}^B_{\rho \cup \{\mathcal Z\}})$ are trace-indistinguishable. (Here $\bar{\mathcal E}_B$ is defined as in Definition 20.)

With (2), we get that for $( st _\mathcal Z,\rho _B)\leftarrow (\mathrm {QExec}^B_{\rho \cup \{\mathcal Z\}}(\eta ,z))$ we have $st _\mathcal Z=\mathcal M(\mathcal E_B( st _B))$ with overwhelming probability.

This, however, implies that $\rho$ is not a minimally secure quantum-passive OT protocol (because it breaks the Alice-security of $\rho$).

If we assume that the Bob-security of $\sigma$ is not fulfilled, we analogously get that the Bob-security of $\rho$ is not fulfilled. (By corrupting Alice instead of Bob.) And finally if the correctness of $\sigma$ is not fulfilled, the correctness of $\rho$ is not fulfilled.

Since $\sigma$ is not minimally secure, it follows that one of the three properties is not fulfilled, and thus $\rho$ is not minimally secure, either. $\square$

Theorem 5

There is no quantum-polynomial-time minimally secure quantum everlasting OT protocol which only uses quantum-passively realizable functionalities (even if we allow it to use several different quantum-passively realizable functionalities and arbitrarily many instances of each).

Proof

For a quantum-polynomial-time protocol, any quantum-passive adversary is computationally bounded during the protocol execution (since he only has to execute the protocol). Thus, the adversaries considered in minimally secure quantum everlasting OT are a superset of those considered in minimally secure quantum-passive OT. $\square$

Corollary 2

There is no quantum-polynomial-time minimally secure everlasting OT protocol which only uses arbitrarily many instances of $\mathcal F_\mathrm {CT}$ (coin-toss), $\mathcal F_\mathrm {CRS}$ (common reference string), $\mathcal F_\mathrm {EPR}$ (predistributed EPR pair), $\mathcal F_\mathrm {PKI}$ (public key infrastructure; assuming that the secret key is uniquely determined by the public key).

Proof

Immediate from Theorem 5 and Lemma 8.$\square$

5 Everlasting Quantum Key Distribution

The first application of quantum everlasting security we present in this paper is a new view on quantum key distribution (QKD). Instead of thinking of QKD as a method for getting unconditionally secure message transmission (but then being stuck with the problem of how to realize authenticated channels), we can combine QKD with a computationally secure authenticated channel to get everlastingly secure message transmission. This was already suggested in [1, Section 3.1], but no formal statement or proof was given, and composition was not considered. The first step is to implement an authenticated channel from, say, a signature card. (All results in this section also hold with a normal public key infrastructure instead of a signature card.)

Lemma 12

(Authenticated channels from signature cards) Let $\mathfrak S$ be a non-uniformly quantum existentially unforgeable signature scheme. Then there is a polynomial-time classical protocol $\pi$ using one instance of $\mathcal F_\mathrm {SC}^{\mathfrak S,A}$ such that $\pi$ eqUC emulates $(\mathcal F_\mathrm {auth}^{A\rightarrow B})^*$.

Proof

The protocol $\pi$ is the following: for each value $sid$, upon the first input $( sid ,m)$ with that $sid$, Alice obtains a signature $\sigma$ on $( sid ,m)$ from $\mathcal F_\mathrm {SC}$ and sends $( sid ,m,\sigma )$ to Bob. (Subsequent inputs $( sid ,m)$ with the same $sid$ are ignored.) When Bob receives a message $( sid ,m,\sigma )$, he checks whether $\sigma$ is a valid signature on $( sid ,m)$. If so, he outputs $( sid ,m)$.

We claim that this protocol $\pi$ eqUC emulates $(\mathcal F_\mathrm {auth}^{A\rightarrow B})^*$. We only show the case with no corruptions (i.e., both Alice and Bob are honest), the other cases are trivial (when sender or recipient is corrupted, $\mathcal F_\mathrm {auth}$ does not provide any guarantees anyway).

Fix a quantum-polynomial-time environment $\mathcal Z$ and a quantum-polynomial-time adversary $\mathrm {Adv}$. The real model then consists of $\mathcal Z$, honest Alice A, honest Bob B, the signature card $\mathcal F_\mathrm {SC}$ and the adversary who intercepts the communication between A and B (and who may communicate with $\mathcal Z$ and can get the public key from $\mathcal F_\mathrm {SC}$). The environment $\mathcal Z$ provides input $( sid ,m)$ to Alice which triggers session $sid$ of the protocol $\pi$, and the environment also gets Bob’s output $( sid ,m)$. (Cf. Fig. 4a.)

Fig. 4

Networks occurring in the proof of Lemma 12

The ideal model consists of $\mathcal Z$, dummy-parties $\tilde{A}$ and $\tilde{B}$ who forward inputs/outputs to and from $(\mathcal F_\mathrm {auth}^{A\rightarrow B})^*$, and simulator $\mathrm {Sim}$ which we will describe below. (Cf. Fig. 4b.)

We have to show that the real model and the ideal model are trace-indistinguishable.

Without loss of generality, we assume that $\mathcal Z$ sends only one message $( sid ,m)$ for each $sid$ to $\mathcal F_\mathrm {auth}^*$. More messages would be ignored anyway.

We use the following quantum-polynomial-time simulator $\mathrm {Sim}$: $\mathrm {Sim}$ internally simulates the machines A, B, and $\mathrm {Adv}$ and forwards communication between them. Communication between $\mathrm {Adv}$ and $\mathcal Z$ is forwarded to the external $\mathcal Z$. Whenever $\mathrm {Sim}$ gets a message $( sid ,m)$ from $\mathcal F_\mathrm {auth}^*$ (meaning that Alice submitted the message m for delivery), $\mathrm {Sim}$ gives input $( sid ,m)$ to the simulated A. When the simulated B outputs $( sid ',m')$ for some $sid '$, then $\mathrm {Sim}$ sends $( sid ',\mathtt {deliver})$ to $\mathcal F_\mathrm {auth}^*$ (causing the message to be delivered that was scheduled for sending in the session $sid$ of $\mathcal F_\mathrm {auth}^*$).

It is easy to see that the real model and ideal model behave identically as long as the following holds in the ideal model: whenever the simulated B outputs $( sid ',m')$, then the session $sid '$ of $\mathcal F_\mathrm {auth}^*$ holds the message $m'$ for delivery.

Hence, we have to show that with overwhelming probability, when B outputs $( sid ',m')$, then $( sid ',m')$ was sent to $\mathcal F_\mathrm {auth}^*$ by $\mathcal Z$ at some earlier point. (And that the message $m'$ was not delivered yet in session $sid '$, but that follows immediately from the construction of Bob: he only outputs one message $( sid ',m')$ for each value for $sid '$.)

Thus, assume that Bob outputs $( sid ',m')$ such that $( sid ',m')$ was never sent to $\mathcal F_\mathrm {auth}^*$. By construction of Bob, this means that he got a message $( sid ',m',\sigma )$ where $\sigma$ is a valid signature on $( sid ',m')$. And by construction of Alice, no signature on $( sid ',m')$ has been requested from $\mathcal F_\mathrm {SC}$ (as Alice only requests such a message after input $( sid ',m')$ to $\mathcal F_\mathrm {SC}$). Thus, Bob got a valid signature on a message that was never signed, in contradiction to the existential unforgeability of $\mathfrak S$. Hence, Bob will output $( sid ',m')$ that was not sent to $\mathcal F_\mathrm {auth}^*$ only with negligible probability; hence, real and ideal models are trace-indistinguishable, and security follows.$\square$

Lemma 13

(Authenticated channels from a PKI) Let $\mathfrak S$ be a quantum existentially unforgeable signature scheme. Let $KG$ denote the key generation algorithm of $\mathfrak S$. There is a polynomial-time classical protocol $\pi$ using one instance of $\mathcal F_\mathrm {PKI}^{A, KG }$ and $\mathcal F_\mathrm {PKI}^{B, KG }$ each such that $\pi$ eqUC emulates $(\mathcal F_\mathrm {auth}^{A \rightarrow B})^*$.

Proof

Analogous to the proof of Lemma 12, except that Alice signs the messages herself (using the secret key from $\mathcal F_\mathrm {PKI}$). $\square$

Lemma 14

(Key exchange from authenticated channels) Let A and B be two parties. Let $\ell$ be an integer. Then there is a polynomial-time protocol $\pi$ using polynomially many instances of $\mathcal F_\mathrm {auth}^{A\rightarrow B}$ and $\mathcal F_\mathrm {auth}^{B\rightarrow A}$ such that $\pi$ eqUC emulates $\mathcal F_\mathrm {KE}^{A,B,\ell }$.

Proof

This was shown to hold for statistical quantum-UC-security (in a slightly different but equivalent model) in [6, 31]. Since statistical quantum-UC-security implies everlasting quantum-UC-security, the lemma follows.$\square$

Lemma 15

(Secure channel from key exchange) Then there is a polynomial-time classical protocol $\pi$ using an instance of $\mathcal F_\mathrm {KE}^{A,B,\eta }$ such that $\pi$ eqUC emulates $\mathcal F_\mathrm {secchan}^{A\rightarrow B}$.

Proof

[32] show that a protocol $\pi$ exists that statistically classically UC emulates $\mathcal F_\mathrm {secchan}^{A\rightarrow B}$. [34] shows that a statistical classical-UC-security implies statistical quantum-UC-security. Finally, statistical quantum-UC-security implies everlasting quantum-UC-security.$\square$

Corollary 3

(Secure channels from signature cards) Let $\mathfrak S$ be a quantum existentially unforgeable signature scheme. There is a polynomial-time protocol $\pi$ using one instance of $\mathcal F_\mathrm {SC}^{A,\mathfrak S}$ and $\mathcal F_\mathrm {SC}^{B,\mathfrak S}$ each such that $\pi$ eqUC emulates $(\mathcal F_\mathrm {secchan}^{A\rightarrow B})^* +(\mathcal F_\mathrm {secchan}^{B\rightarrow A})^*$. (I.e., we have a bidirectional multi-message secure channel.)

Proof

By composing the protocols from Lemma 14 and Lemma 15, we get a protocol $\pi '$ that uses polynomially many instances of $\mathcal F_\mathrm {auth}^{A\rightarrow B}$ and $\mathcal F_\mathrm {auth}^{B\rightarrow A}$ and that eqUC emulates $(\mathcal F_\mathrm {secchan}^{A\rightarrow B})^* + (\mathcal F_\mathrm {secchan}^{B\rightarrow A})^*$. Instead of polynomially many instances of $\mathcal F_\mathrm {auth}^{A\rightarrow B}$ and $\mathcal F_\mathrm {auth}^{B\rightarrow A}$, we can just use one instance of $(\mathcal F_\mathrm {auth}^{A\rightarrow B})^*$ and $(\mathcal F_\mathrm {auth}^{B\rightarrow A})^*$ each. Composing $\pi '$ with the protocol from Lemma 12 (one instance for realizing $(\mathcal F_\mathrm {auth}^{A\rightarrow B})^*$ and one for realizing $(\mathcal F_\mathrm {auth}^{B\rightarrow A})^*$), we get a protocol $\pi$ using one instance of one instance of $\mathcal F_\mathrm {SC}^{A,\mathfrak S}$ and $\mathcal F_\mathrm {SC}^{B,\mathfrak S}$ each and that eqUC emulates $(\mathcal F_\mathrm {secchan}^{A\rightarrow B})^* + (\mathcal F_\mathrm {secchan}^{B\rightarrow A})^*$.$\square$

6 Everlasting Quantum Multi-party Computation

Classical everlasting UC commitments In the classical setting, Müller-Quade and Unruh [27] presented a protocol that everlastingly classical-UC emulates (called “long-term UC emulates” there, ecUC emulates in the following) the commitment functionality $\mathcal F_\mathrm {COM}$ and that uses a signature card $\mathcal F_\mathrm {SC}$. There protocol cannot be proven secure in the quantum setting (at least we do not know how), but it is instructive to understand their protocol before we present ours.¹¹

In order for a commitment protocol to be everlastingly UC secure, we need to achieve the following: obviously, it needs to be statistically hiding and computationally binding. Furthermore, we need that the protocol is extractable: a simulator who controls the signature card can find out what value Alice committed to. And the protocol needs to be equivocal: a simulator who controls the signature card can cheat the binding property and open to a different value. The simulators need to behave in a way that is statistically indistinguishable from the honest behavior of the parties.

The difficulty lies in the extractability. If the committed value can be extracted by the simulator from the interaction, then it must be somehow contained in that interaction, and an unlimited entity can extract it. But that would contradict the statistical hiding property. The approach is to use the signature card $\mathcal F_\mathrm {SC}^A$. When Alice wishes to commit to a value m, we force her to obtain a signature on m. Since the simulator controls $\mathcal F_\mathrm {SC}$, and since Alice can only sign using $\mathcal F_\mathrm {SC}$ (even the owner of the signature card does not know the secret key), the simulator will learn m. How do we force Alice to sign m? First, Alice commits to m using a commitment $\mathrm {COM}$. Then Alice obtains a signature $\sigma$ on (m, u) from $\mathcal F_\mathrm {SC}$ where u is the opening information for $\mathrm {COM}(m)$. And then Alice proves that she knows a signature $\sigma$ on (m, u) for some u that opens $\mathrm {COM}(m)$ as m. (Here $\mathrm {COM}$ is statistically hiding, and the proof is a statistically witness-indistinguishable argument of knowledge.)

We now have extractability: Alice can only succeed in the proof if she gets a signature on (m, u). But then all the simulator has to do is to check which query (m, u) to $\mathcal F_\mathrm {SC}$ opens the commitment c, and then he knows m. (We explain the “or I know the secret key”-part in a moment.) In the open phase, we cannot just send u, then we would not have equivocality. Instead, Alice proves that she could open c as m:

Now, if the simulator wishes to equivocate, he simply commits to 0, and later he produces a fake proof that he can open c as m. To produce this fake proof, we have added the “or I know the secret key $sk$”-part. Since the simulator knows $sk$ (he controls $\mathcal F_\mathrm {SC}$), he can always perform the proof using $sk$ as witness. (While Alice, not knowing $sk$, is forced to prove the part of the statement before the “or.”)

Difficulties in the Quantum Case Now assume we wish to prove the above protocol secure in the quantum case. Then instead of an argument of knowledge, we need to use a quantum argument of knowledge. But then we run into problems when showing extractability. To show extractability, we need to show that Alice cannot perform the first proof without first sending (m, u) to $\mathcal F_\mathrm {SC}$. To do so, consider an execution where Alice performs the proof without sending (m, u) to $\mathcal F_\mathrm {SC}$. We can then consider Alice as a prover $A^{\mathcal O}$ with access to a signing oracle $\mathcal O$. (That is, when queried with a message m, $\mathcal O$ returns a signature on m.) Applying the extractor E from the argument of knowledge to Alice, we get that $E^{A^{\mathcal O}}$ outputs a witness to the statement that is proven. I.e., either a signature on (m, u) or the secret key $sk$ of $\mathcal O$. Since $E^{A^\mathcal O}$ has only black-box access to $\mathcal O$, and since $A^\mathcal O$ and thus also $E^{A^\mathcal O}$ never signs (m, u), both possibilities contradict the existential unforgeability of the signature scheme. This reasoning works in the classical case. In the quantum case (following [36]), however, the extractor $E^{A^\mathcal O}$, while rewinding, does the following: it applies both U and $U^{-1}$ where U is the unitary transformation describing the operation of $A^\mathcal O$. Thus, indirectly $E^{A^\mathcal O}$ invokes not only $\mathcal O$, but also its inverse. Existential unforgeability makes no statement in this case. It could well be that given access to the inverse of $\mathcal O$, we can efficiently construct forgeries or even extract the secret key.

Note: At a first glance, it might seem that invoking the inverse of $\mathcal O$ is not a problem due to the following reasoning. An oracle $\mathcal O$ implementing a function f(x) is usually modeled as a unitary mapping ${\left| {x}\right\rangle }{\left| {y}\right\rangle }$ to ${\left| {x}\right\rangle }{\left| {y\oplus f(x)}\right\rangle }$. That unitary is self-inverse, so applying $\mathcal O^{-1}$ is equivalent to applying $\mathcal O$.

However, if the signing oracle $\mathcal O$ is modeled in this way, then it can be queried on superposition. Instead, $\mathcal O$ should measure the message to be signed first. This could be realized by copying the message (using CNOTs) into fresh ancillae bits. But then $\mathcal O$ is not self-inverse any more. Furthermore, to formulate the existential unforgeability, $\mathcal O$ additionally needs to keep track of all messages that were signed (otherwise it is not possible to define a “fresh” forgery). Applying the inverse of $\mathcal O$ will remove messages from this list, making the notion of a fresh message meaningless.

Another (quantum) view on the problem. It has been pointed out (by an anonymous reviewer) that in the quantum case, the problem is actually the following: using a standard unconditionally hiding commitment scheme fails to achieve everlasting security when using it to construct an OT. But this is not due to composability issues, but to the fact that commitment schemes do not force the committer to commit to a classical value, allowing commitments to superpositions instead. In contrast, an ideal commitment functionality would not allow the commit to occur in superposition. This also matches what we do in our quantum-secure protocol below: The signature card forces the committed message to be classical.

We believe this view to be correct, too. Indeed, our protocol would not work if the signature card would allow the adversary to sign superpositions of messages. Yet, this view only partially explains the situation: even in the purely classical case described above, standard commitments are not sufficient. But in the classical case, the possibility of committing to superpositions obviously cannot be the reason for the problem, indicating that composition is at least part of the problem. In fact, we believe that non-composition and the possibility to commit to superpositions might actually be two sides of the same coin. For example, composition usually requires extractability, i.e., the fact that the adversary can only commit to values he knows. But if the adversary can commit to superpositions, he cannot know what he commits to. It would be interesting (but beyond the scope of this work) to explore this connection further.

Fig. 5

The commitment protocol based on signature cards—overview. Proof 1 is a witness-indistinguishable argument of knowledge, proof 2 is a statistically witness-indistinguishable argument

Our Approach To solve this problem, we need to construct a new protocol in whose security proof we do not need to rewind the signing oracle. A protocol overview is given in Fig. 5. We now explain the intuition behind the protocol. As explained above, the main challenge is the extractability of the protocol: Alice commits to m using a commitment scheme $\mathrm {COMB}$, the unveil information is $u_m$. We need to make sure that Alice is forced to sign $(m,u_m)$ in order to complete the protocol. We cannot just perform a proof of knowledge that Alice knows such a signature $\sigma$ on $(m,u_m)$—it might be that Alice proves that she knows a signatures without actually knowing it. To force Alice to actually know the signature, we use the following approach: During the commit phase, Alice commits to $(\sigma ,m,u_m)$ using a commitment scheme $\mathrm {COMX}$. ($c_\sigma :=\mathrm {COMX}((\sigma ,m,u_m))$.) And additionally, we let Alice prove (“proof 2” in Fig. 5) that the resulting commitment $c_\sigma$ indeed contains a valid signature $\sigma$ on $(m,u_m)$. However, we seem to have the same problem as before: how do we guarantee that Alice knows the content of the resulting commitment $c_\sigma$? We cannot use rewinding for the same reason as before. Instead, we use a so-called dual-mode commitment for $c_\sigma$. A dual-mode commitment $\mathrm {COMX}$ depends on a public parameter $crs$: If $crs$ is honestly chosen, then $\mathrm {COMX}$ is statistically hiding. (We need this as otherwise the overall protocol would not be statistically hiding and thus not everlastingly secure). But $crs$ can also be chosen in a special way together with a trapdoor $td$ such that using $td$, we can efficiently compute $(\sigma ,m,u_m)$ given $c_\sigma =\mathrm {COMX}( crs ,(\sigma ,m,u_m))$.

Then we can prove extractability of the eqUC commitment protocol roughly as follows:

• 1. For extracting, the simulator looks at the list of signing queries to $\mathcal F_\mathrm {SC}$ and finds a suitable pair $(m,u_m)$. We need to show that if Alice opens successfully, there must have been such a signing query for $(m,u_m)$ during the commit phase.

• 2. To show that, consider a game consisting of an execution with corrupted Alice and that simulator. We change the game such that instead of picking $crs$ honestly, we pick it together with a trapdoor $td$. (We discuss below how to do that.)

  Note: the new game will only be computationally indistinguishable from the preceding one. But this does not contradict everlasting security: we are in a side-arm of the proof in order to bound the probability of a certain event (“Alice opens without signing $(m,u_m)$”). The extracting simulator will still be statistically indistinguishable from an honest recipient of the commitment since the extracting simulator just passively looks at the signing queries.

• 3. We use the soundness of “proof 2” to show that $c_\sigma$ contains with overwhelming probability a valid signature $\sigma$ on $(m,u_m)$. (In the full proof, we need to additionally exclude that Alice proves the alternative option that $c_ sk$ contains the secret key.)

  Note: we do not claim at this point that Alice knows $\sigma$, we only show that whatever is extracted from $c_\sigma$ using $td$ is a valid signature on $(m,u_m)$. In particular, we do not use the unforgeability of the signature scheme in this step.

• 4. Now we use the unforgeability: we have derived that extracting $c_\sigma$ using $td$ produces a signature on $(m,u_m)$. If this would be the case without having sent $(m,u_m)$ to $\mathcal F_\mathrm {SC}$, we would have produced a forgery, contradicting unforgeability.

• 5. So Alice always signs $(m,u_m)$; hence, the simulator from Step 1 succeeds with overwhelming probability in extracting.

One thing is missing in this description: how to pick $crs$ in a way that we can choose it together with a trapdoor in Step 2? For this, we have the setup phase in Fig. 5. Here $crs$ is chosen using a coin-toss that is designed such that Bob, if he knows a signature on a special message $\mathtt {msg1}$, can cheat and choose $crs$ arbitrarily. In Step 2, this allows us to pick $crs$ together with a trapdoor by requesting a signature $\mathtt {msg1}$ from $\mathcal F_\mathrm {SC}$. (Here $\mathtt {msg1}$ is an arbitrary fixed bitstring, but syntactically different from all other messages occurring in the protocol.)

Notice that “proof 1” in the coin-toss protocol needs to be “of knowledge” (more precisely, a witness-indistinguishable argument of knowledge). However, we do not run into problems with the combination of rewinding and unforgeability this time, because during the execution of “proof 1,” the signature card is not accessed by the honest verifier Alice. (And thus the signing oracle is not accessed by the extractor at all.)

Thus, the protocol from Fig. 5 is extractable.

Finally, we need to see how to achieve equivocality. Fortunately, this is easy: the equivocating simulator commits to the secret key $sk$ of $\mathcal F_\mathrm {SC}$ in the commitment $c_ sk$ (he knows it since he controls $\mathcal F_\mathrm {SC}$) and commits to 0 in $c_\sigma$. Then, in the open phase, to open as an arbitrary m, the simulator just performs “proof 2” using the fact that $c_ sk$ indeed contains $sk$. Thus, the protocol is equivocal, too. (No fake CRS is needed in this case.)

The actual proof of eqUC-security can be nicely structured as a sequence of game transformation and is presented in the next section.

6.1 Protocol Description and Proof

We fix the following notation for interactive commitment schemes: if $\mathrm {COM}$ is a commitment scheme, we denote by $(c,u)\leftarrow \mathrm {COM}_{C,R}(1^\eta ,m)$ an execution of the commit phase with sender C and recipient R where C commits to the message m. After the protocol execution, both C and R know the value c (e.g., c could be the protocol transcript), intuitively c represents the commitment itself. Furthermore, C gets the value u, the opening information. We assume that the opening phase consists of C sending (m, u), and R verifying the open phase via a deterministic function $\mathrm {COMVerify}(c,m,u)$. For commitments that take a public parameter $crs$, we add this parameter as an additional argument to $\mathrm {COM}_{C,R}$ and $\mathrm {COMVerify}$.

We now give a definition of dual-mode commitments. The definition is close to that of dual-mode commitments in [12]. The main difference is that we additionally require that the honestly chosen CRS is uniformly chosen from a set $CRS$. As discussed in [12], dual-mode commitments (also according to our definition) can be constructed from Regev’s cryptosystem [30].

Definition 22

A dual-mode commitment $\mathrm {COM}$ is an interactive commitment with a public common reference string $crs$ and which has the following properties:

• The common reference string $crs$ is chosen from a set $CRS$ such that one can efficiently sample elements of $CRS$ that are statistically indistinguishable from uniform, and such that $CRS$ is endowed with an arbitrary group operation $*$ (e.g., $CRS$ could be $\{0,1\}^{n}$ or $\mathbb {Z}_n$ for some n). The operation $*$ is efficiently computable, and inverses with respect to $*$ are efficiently computable.

• Statistical hiding: For $crs$ chosen uniformly from $CRS$, $\mathrm {COM}$ is statistically hiding.

• Fake CRS: There is an algorithm $( crs , td )\leftarrow \mathrm {COMFakeCRS}(1^\eta )$ such that $crs$ is non-uniformly quantum-computationally indistinguishable from being uniformly distributed on $CRS$.

• Extractability: There is an efficient algorithm $\mathrm {COMExtract}$ such that for any non-uniform quantum-polynomial-time A, we have that the following probability is negligible:

  

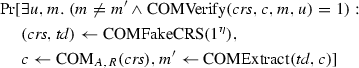
  Here $c\leftarrow \mathrm {COM}_{A,R}( crs )$ stands, in abuse of notation, for a commit phase between the adversary A and an honest recipient R. And c denotes the value that R gets at the end of the commit phase.

Furthermore, we will need a signature scheme $\mathfrak S$ that has some (very natural) additional properties besides quantum existential unforgeability. First, we will need deterministic verification. This just means that the verification algorithm is not randomized. Second, we will need that $\mathfrak S$ has a $\mathrm {matchingKeys}$-predicate. This means that there is a predicate $\mathrm {matchingKeys}$ that can be decided in deterministic polynomial-time, and such that for $pk , sk$ chosen according to the key generation algorithm, we have $\mathrm {matchingKeys}( pk , sk )=1$ with overwhelming probability. And given $pk$ as chosen by the key generation, a quantum-polynomial-time algorithm outputs $sk$ with $\mathrm {matchingKeys}( pk , sk )=1$ only with negligible probability. (Intuitively, this just means that there is a well-defined concept of whether a given secret key matches a given public key.)

Fig. 6

The commitment protocol based on signature cards

$\mathrm {WIAOK}_{ ct }$ is a quantum-computationally witness-indistinguishable quantum argument of knowledge for the relation $R_{ ct }$. $\mathrm {SWIA}_{ com }$ is a statistically witness-indistinguishable argument for the relation $R_{ com }$. $\mathrm {COMH}$ is a statistically hiding quantum-computationally binding commitment. $\mathrm {COMB}$ is a quantum-computationally hiding perfectly binding commitment. $\mathrm {COMX}$ is a dual-mode commitment

Theorem 6

(Commitments from signature cards) Let A and B be parties. Let $\ell$ be an integer. Assume the existence of (all computational assumptions against non-uniform adversaries): quantum-computationally witness-indistinguishable quantum arguments of knowledge, statistically witness-indistinguishable quantum arguments,¹² statistically hiding quantum-computationally binding commitments, quantum-computationally hiding perfectly binding commitments, dual-mode commitments. Assume that $\mathfrak S$ is a quantum existentially unforgeable signature scheme with deterministic verification and with $\mathrm {matchingKeys}$-predicate.

Then there is a protocol $\pi$ using secure channels and one instance of $\mathcal F_\mathrm {SC}^{A,\mathfrak S}$ such that $\pi$ eqUC emulates $(\mathcal F_\mathrm {COM}^{A\rightarrow B,\ell })^*$.

(Here $(\mathcal F_\mathrm {COM}^{A\rightarrow B,\ell })^*$ is the functionality consisting of many instances of $\mathcal F_\mathrm {COM}^{A\rightarrow B,\ell }$. I.e., we can perform many commitments using a single signature card.)

Proof

Fix a bitstrings $\texttt {msg1}$. We assume that tuples are encoded such that $\texttt {msg1}$ is distinct from any tuple. Let $\mathrm {COMB}$ denote a perfectly binding and quantum-computationally hiding commitment scheme. Let $\mathrm {COMH}$ denote a statistically hiding quantum-computationally binding commitment scheme. Furthermore, let $\mathrm {COMX}$ be a dual-mode commitment. Let $CRS$ denote the set from which the parameter of $\mathrm {COMX}$ is chosen. We assume that the message space of $\mathrm {COMH}$ contains $\{0,1\}^{\ell }$, that the message space of $\mathrm {COMX}$ is chosen large enough to commit on triples $(\sigma ,m,u)$ where $m\in \{0,1\}^{\ell }$, u is the opening information of $(c,u)\leftarrow \mathrm {COMH}(m)$, and $\sigma$ is a signature on (m, u), and that the message space of $\mathrm {COMX}$ is large enough to commit to the secret key of the signature card. Finally, we assume that the message space of $\mathrm {COMB}$ contains $CRS$. (Notice that the message space can be assumed to be arbitrarily large, because we can just concatenate several commitments of smaller message space to get a bigger one.)

Let $\mathrm {Verify}$ be the verification algorithm of $\mathfrak S$. We define the following NP-relations $R_{ ct }$ and $R_{ com }$:

Let $\mathrm {WIAOK}_{ ct }$ be a quantum-computationally witness-indistinguishable quantum argument of knowledge for the relation $R_{ ct }$. Let $\mathrm {SWIA}_{ com }$ be a statistically witness-indistinguishable quantum argument for the relation $R_{ com }$.

We describe our commitment protocol $\pi$ in Fig. 6. We claim that $\pi$ is a eqUC-secure commitment protocol (that allows to perform many commitments), i.e., $\pi$ eqUC emulates $(\mathcal F_\mathrm {COM}^{A\rightarrow B,\ell })^*$.

Corrupted Bob We first show security in the case of Bob being corrupted. The real model and ideal model in this case are as follows:

In the real model, we have the environment $\mathcal Z$, the adversary $\mathrm {Adv}$, the honest party A (Alice), the corrupted party $B^C$. A and $B^C$ can communicate with the signature card $\mathcal F_\mathrm {SC}$ (only A can sign). The adversary controls the corrupted party $B^C$, so effectively he controls the communication between Alice and Bob and can get the public key from $\mathcal F_\mathrm {SC}$ via $B^C$. The environment provides Alice’s inputs $( sid ,\mathtt {commit},v)$ and $( sid ,\mathtt {open})$. In the following, we omit the argument $sid$ for readability. One should, however, always keep in mind that the commit and open phases of several sessions can be running concurrently (but only one setup phase). See Fig. 7a.

Fig. 7

Networks occurring in the case of corrupted Bob

In the ideal model, we have the environment $\mathcal Z$, the simulator $\mathrm {Sim}$ (to be defined below), the dummy-party $\tilde{A}$, the corrupted party $B^C$, and the commitment functionality $\mathcal F_\mathrm {COM}$. The inputs $(\mathtt {commit},v)$ and $\mathtt {open}$ of $\mathcal F_\mathrm {COM}$ are provided by the dummy-party $\tilde{B}$ and thus effectively by the environment $\mathcal Z$. The simulator $\mathrm {Sim}$ controls the corrupted party $B^C$ and hence gets the outputs $\mathtt {committed}$ and $(\mathtt {open},v)$ of $\mathcal F_\mathrm {COM}$. See Fig. 7b.

Fix a quantum-polynomial-time adversary $\mathrm {Adv}$. To show security, we need to find a quantum-polynomial-time simulator $\mathrm {Sim}$ such that, for any quantum-polynomial-time environment $\mathcal Z$, the real model and the ideal model are trace-indistinguishable.

To show that the real and the ideal model are trace-indistinguishable, we start with the real model, and change the machines in the real model step-by-step until we end up with the ideal model. In each step, we show that the network before and after that step is trace-indistinguishable. We describe the simulator $\mathrm {Sim}$ in the last step of the proof.

As the simulator will have to simulate the messages sent by Alice, but does not know the committed message m before the open phase, the simulator will have to “cheat” in the commitment by first committing to an arbitrary value and later opening this value as m (equivocality). In order to arrive at such a simulator, we step-by-step transform Alice in the honest execution into an Alice that also “cheats,” this Alice can then be used directly to construct the simulator in the end.

Thus, for the following sequence of games, fix a quantum-polynomial-time environment $\mathcal Z$ and a quantum-polynomial-time adversary $\mathrm {Adv}$. In slight abuse of notation, we call two games trace-indistinguishable if the states output by $\mathcal Z$ in both games is trace-indistinguishable.

We describe the differences between the games in terms of changes of the behavior of Alice. It is understood that all these changes apply to all sessions of the protocol.$\square$

Game 1

An execution of the real model as in Fig. 7a. $\square$

Game 2

Like Game 1, except that in step C3, Alice executes $(c_{ sk },u_{ sk })\leftarrow \mathrm {COMX}_{A,B}( crs , sk )$ instead of $(c_{ sk },u_{ sk })\leftarrow \mathrm {COMX}_{A,B}( crs ,0)$. (Here $sk$ is the secret key maintained by the ideal functionality $\mathcal F_\mathrm {SC}$.) $\square$

Notice that in this game, Alice is not a valid protocol machine because her behavior depends on $sk$ which is a local variable of $\mathcal F_\mathrm {SC}$. It is, however, not necessary that Game 2 is a valid protocol execution in our model as long as it is well-defined. The final game in our sequence (involving a simulator) will again be a valid execution in the ideal model.

From the statistical hiding property of dual-mode commitments, it follows that there exists a negligible function $\mu _1$ and a set $H\subseteq CRS$ of common reference strings (where H may depend on the security parameters) such that: $|H|/| CRS |\ge 1-\mu _1(\eta )$ (i.e., with overwhelming probability, a CRS in H will be chosen) and for any fixed $crs \in H$, we have that $\mathrm {COMX}( crs ,\cdot )$ is statistically hiding (with trace distance at most $\mu _1$).

Let $P_{i}^H$ denote the probability that $\mathrm {WIAOK}_{ ct }$ in step S5 succeeds and for the $crs$ computed in step S6 of the setup phase in the execution of Game i it holds that $crs \notin H$. Then if $P^H_1$ is negligible, Game 1 and Game 2 are trace-indistinguishable (notice that the opening information $u_ sk$ is never used).

Game 3

Like Game 2, except that in step O2, in the $\mathrm {SWIA}_{ com }$, Alice uses the witness $(0, sk ,0,0,u_ sk )$ instead of $(\sigma ,0,u_m,u_\sigma ,0)$. $\square$

Both $(0, sk ,0,0,u_ sk )$ instead of $(\sigma ,0,u_m,u_\sigma ,0)$ are valid witnesses for the statement $( crs , pk ,c_m,c_\sigma ,c_ sk ,m)$. Thus, the statistical witness-indistinguishability of $\mathrm {SWIA}_{ com }$ implies that Game 2 and Game 3 are trace-indistinguishable. (Since several instances of the $\mathrm {SWIA}_{ com }$ are executed, we use a standard hybrid-argument.)

Game 4

Like Game 3, except that in step C3, Alice executes $(c_\sigma ,u_\sigma )\leftarrow \mathrm {COMX}_{A,B}( crs ,0)$ instead of $(c_\sigma ,u_\sigma )\leftarrow \mathrm {COMX}_{A,B}( crs ,(\sigma ,m,u_m))$. $\square$

Analogous to the trace-indistinguishability of Game 1 and Game 2, we have that if $P^H_{3}$ is negligible, Game 3 and Game 4 are trace-indistinguishable (notice that due to the change of witness in Game 3, the opening information $u_\sigma$ is never used).

Game 5

Like Game 4, except that step C2 is omitted. (I.e., Alice does not obtain the signature $\sigma$.) $\square$

Notice that in Game 4, the signature $\sigma$ is never used. (We removed it from the witness of $\mathrm {SWIA}_{ com }$ in Game 3, and from the commitment $c_\sigma$ in Game 4.) Thus, the output state of $\mathcal Z$ in Game 4 and Game 5 is equal.

Game 6

Like Game 5, except that in step C1 of the commit phase, Alice executes $(c_m,u_m)\leftarrow \mathrm {COMH}_{A,B}(0)$ instead of $(c_m,u_m)\leftarrow \mathrm {COMH}_{A,B}(m)$. $\square$

Since the opening information $u_m$ is never used (we removed it from the witness in Game 3, and from the commitment $c_\sigma$ in Game 4, and from the message sent to $\mathcal F_\mathrm {SC}$ in Game 5), and since $\mathrm {COMH}$ is statistically hiding, Game 5 and Game 6 are trace-indistinguishable. (Since several instances of the $\mathrm {COMH}$ are executed, we use a standard hybrid-argument.)

Notice that in Game 6, Alice uses the value m only during the open phase. We can thus construct a simulator $\mathrm {Sim}$ that does the following: it internally simulates the modified Alice from Game 6 together with the ideal functionality $\mathcal F_\mathrm {SC}$. When $\mathrm {Sim}$ gets the message $\mathtt {committed}$ from $\mathcal F_\mathrm {COM}$ (this happens if $\mathcal Z$ sends $(\mathtt {commit},m)$ to Alice), he invokes the modified Alice with input $(\mathtt {commit},*)$. When $\mathrm {Sim}$ gets the message $(\mathtt {open},m)$ from $\mathcal F_\mathrm {COM}$, he puts the correct value of m into Alice’s state (m instead of $*$) invokes the Alice with input $\mathtt {open}$. Communication of Alice with Bob is forwarded to the environment (as the dummy-adversary $\mathrm {Adv}$ would do in the real model and Game 6).

Game 7

An execution of the ideal model as in Fig. 7b using the simulator $\mathrm {Sim}$ we just defined. $\square$

Game 7 executes the same steps as Game 6. The only difference is that some computations are performed by different machines (e.g., $\mathrm {Sim}$ takes over the computations of $\mathcal F_\mathrm {SC}$ and Alice). Thus, $\mathcal Z$’s output state in Game 6 and Game 7 is identical.

Thus, if $P^H_{1}$ and $P^H_{}$ are negligible, then Game 1 and Game 7 are trace-indistinguishable, and hence, $\pi$ eqUC emulates $(\mathcal F_\mathrm {COM}^{A\rightarrow B,\ell })^*$ in the case of corrupted Bob.

It remains to show that $P^H_{1}$ and $P^H_{}$ are negligible. We show this for $P^H_{1}$, the case for $P^H_{}$ is completely analogous. Assume that $P^H_{1}$ is non-negligible. The following sequence of games will then lead to a contradiction.

Game 8

Like Game 1, except that we abort the game after the setup phase (i.e., after step S6). $\square$

Whether $crs \in H$ holds is determined at the end of the setup phase. Thus, aborting after the setup phase does not change whether $crs \in H$ holds. Hence, $P^H_{1}=P^H_{8}$ and thus $P^H_{8}$ is non-negligible.

Since $\mathrm {COMB}$ is perfectly binding, there is a (not necessarily efficiently computable) function $f^B$ that extracts the committed value a commitment. More precisely, for any c, m, and u, we have $\mathrm {COMBVerify}(c,m,u)=1\Longrightarrow f^B(c)=m$. (If c cannot be opened, then the value of $f^B(c)$ does not matter to us.)

Since $k_1$ is chosen uniformly from $CRS$ after $c_k$ has been chosen, and since $|H|/| CRS |$ is overwhelming, we have that $\Pr [f^B(c_k)*k_1\in H:Game~8]$ is overwhelming. Furthermore, since $crs =k_0*k_1$, by definition of $P^H_{8}$, we have that $\Pr [k_0*k_1\notin H\wedge \mathrm {WIAOK}_{ ct }\text { succeeds}:Game~8]$ is non-negligible. Together, this gives that $\Pr [k_0\ne f^B(c_k)\wedge \mathrm {WIAOK}_{ ct }\text { succeeds}:Game~8]$ is non-negligible.

Observe that the execution of Game 8 can be split into two phases as follows: the first phase consists of an execution of the real model until step S4 inclusive. We denote the execution of the first phase by an efficient algorithm $G_0$. $G_0$ uses a signing oracle $\mathcal O$ whenever $\mathcal F_\mathrm {SC}$ produces a signature. $G_0$ returns the values $pk ,c_k,k_0$ and its final state $\rho _0$.

The second phase consists of the execution of $\mathrm {WIAOK}_{ ct }$ with honest verifier (using statement $( pk ,c_k,k_0)$) and some efficient, potentially malicious prover $P^*(\rho _0)$ (that includes all machines in the game except for Alice). Note that in the second phase the signature card is never used for signing. (Only Alice can sign, and the protocol does not instruct Alice to sign during the setup phase.) Thus, $P^*$ does not need access to $\mathcal O$. Furthermore, without loss of generality, we can assume $P^*$ to be unitary. We can thus reformulate Game 8 as follows:

Game 9

Let $\mathcal O$ be a signing oracle. Let V denote the honest verifier of $\mathrm {WIAOK}_{ ct }$. Execute $(\rho _0, pk ,c_k,k_0)\leftarrow G_0^\mathcal O$. Execute $ok \leftarrow \langle P^*(\rho _0),V( pk ,c_k,k_0)\rangle$. (That is, $ok$ represents V’s output.) $\square$

(The notation $\langle A,B\rangle$ denotes the output of B after an interaction between A and B.) Then $\Pr [k_0\ne f^B(c_k)\wedge ok =1:Game~xm{9}]= \Pr [k_0\ne f^B(c_k)\wedge \mathrm {WIAOK}_{ ct }\text { succeeds}:Game~8]$ is non-negligible.

Game 10

Execute $(\rho _0, pk ,c_k,k_0)\leftarrow G_0^\mathcal O$. Execute $(u,\sigma )\leftarrow E^{P^*}(\rho _0^{( pk ,c_k,k_0)})$. Here E is the extractor of $\mathrm {WIAOK}_{ ct }$. $\square$

For any value of $pk ,c_k,k_0$, let $\rho _0^{( pk ,c_k,k_0)}$ be the state output by $G_0^\mathcal O$ when $G_0^\mathcal O$ outputs $pk ,c_k,k_0$. And let $\Pr _{ pk ,c_k,k_0}$ denote the probability that $G_0^\mathcal O$ outputs these values $pk ,c_k,k_0$. Since $\mathrm {WIAOK}_{ ct }$ is a quantum argument of knowledge, there is an integer $d\ge 1$ and a negligible function $\mu$ such that for all $pk ,c_k,k_0$

$$\begin{aligned}&\Pr [(( pk ,c_k,k_0),(u,\sigma ))\in R_{ ct }: (u,\sigma )\leftarrow E^{P^*}(\rho _0^{( pk ,c_k,k_0)})] \nonumber \\&\quad \ge \bigl (\Pr [ ok =1 : ok \leftarrow \langle P^*(\rho _0),V( pk ,c_k,k_0),]\rangle \bigr )^d -\mu \end{aligned}$$

(3)

We abbreviate the first probability by $\Pr _E^{( pk ,c_k,k_0)}$ and the second as $\Pr _V^{( pk ,c_k,k_0)}$. Averaging over the different possible values of $( pk ,c_k,k_0)$, we get

Here $(*)$ uses Jensen’s inequality. Since we have shown above that $\Pr [k_0\ne f^B(c_k)\wedge ok =1:Game~9]$ is non-negligible, with (4) we get that $\Pr [ k_0\ne f^B(c_k) \wedge (( pk ,c_k,k_0),(u,\sigma ))\in R_{ ct }: Game~10]$ is non-negligible, too.

By definition of $f^B$, we have that if $k_0\ne f^B(c_k)$, then $\mathrm {COMBVerify}(c_k,k_0,u)=0$. Thus, $k_0\ne f^B(c_k) \wedge (( pk ,c_k,k_0),(u,\sigma ))\in R_{ ct }$ implies $\mathrm {Verify}( pk ,\sigma ,\mathtt {msg1})=1$ by definition of $R_{ ct }$. Thus, $\Pr [\mathrm {Verify}( ok ,\sigma ,\mathtt {msg1})=1 : Game~10]$ is non-negligible.

In Game 10, the signing oracle $\mathcal O$ is only queried by $G_0^\mathcal O$. By construction of $G_0$, this means that $\mathcal O$ only signs messages that Alice would send to $\mathcal F_\mathrm {SC}$. Alice never sends $\mathtt {msg1}$ to $\mathcal F_\mathrm {SC}$ (since $\mathtt {msg1}$ is distinct from any tuple $(m,u_m)$.). Thus in Game 10, the message $\texttt {msg1}$ is never sent to the signing oracle $\mathcal O$. Thus, the existential quantum unforgeability of $\mathfrak S$ implies that $\Pr [\mathrm {Verify}( ok ,\sigma ,\mathtt {msg1})=1 : Game~10]$ is negligible. Thus, we reached a contradiction. Hence, our assumption that $P^H_{1}$ is non-negligible (see the paragraph before Game 8) was wrong. Hence $P^H_{1}$ is negligible. Analogously we show that $P^H_{}$ is negligible. After Game 7 we concluded, that if $P^H_{1}$ and $P^H_{}$ are negligible, $\pi$ eqUC emulates $(\mathcal F_\mathrm {COM}^{A\rightarrow B,\ell })^*$ in the case of corrupted Bob.

Thus, we have shown that $\pi$ eqUC emulates $(\mathcal F_\mathrm {COM}^{A\rightarrow B,\ell })^*$ in the case of corrupted Bob.

Corrupted Alice First, we describe the structure of the real and the ideal model in the case that the party A (Alice) is corrupted:

In the real model, we have the environment $\mathcal Z$, the adversary $\mathrm {Adv}$, the corrupted party $A^C$, and the honest party B (Bob). $A^C$ and B can communicate with the signature card $\mathcal F_\mathrm {SC}$ (only $A^C$ can sign). The adversary controls the corrupted party $A^C$, so effectively he controls the communication between Alice and Bob and can access $\mathcal F_\mathrm {SC}$ in Alice’s name. The environment gets Bob’s outputs $( sid ,\mathtt {committed})$ and $( sid ,\mathtt {open},v)$. In the following, we omit the argument $sid$ for readability. One should, however, always keep in mind that the commit and open phases of several sessions can be running concurrently (but only one setup phase). See Fig. 8a.

Fig. 8

Networks occurring in the case of corrupted Alice

In the ideal model, we have the environment $\mathcal Z$, the simulator $\mathrm {Sim}$ (to be defined below), the corrupted party $A^C$, the dummy-party $\tilde{B}$, and the commitment functionality $\mathcal F_\mathrm {COM}$. The inputs $(\mathtt {commit},v)$ and $\mathtt {open}$ of $\mathcal F_\mathrm {COM}$ are provided by the corrupted party $A^C$ and thus effectively by the simulator $\mathrm {Sim}$. The environment $\mathcal Z$ controls the dummy-party $\tilde{B}$ and hence gets the outputs $\mathtt {committed}$ and $(\mathtt {open},v)$ of $\mathcal F_\mathrm {COM}$. See Fig. 8b.

Fix a quantum-polynomial-time adversary $\mathrm {Adv}$. To show security, we need to find a quantum-polynomial-time simulator $\mathrm {Sim}$ such that for any environment $\mathcal Z$, the real model and the ideal model are trace-indistinguishable.

Before we will describe the simulator $\mathrm {Sim}$, we first investigate the real model further. In an execution of the protocol, for a given session id $sid$, we call a pair (m, u) $sid$-valid if $\mathrm {COMHVerify}(c_m,m,u)=1$ where $c_m$ is the commitment from C1 in session $sid$. We call a triple $(\sigma ,m,u)$ $sid$-valid if (m, u) is $sid$-valid and $\mathrm {Verify}( pk ,\sigma ,(m,u))=1$ where $pk$ is the public key of $\mathcal F_\mathrm {SC}$. Let $sigqueries$ denote the list of messages that have been sent to the $\mathcal F_\mathrm {SC}$ for signing. (Notice that one list $sigqueries$ is shared between all sessions because it is not possible to tell which signing query belongs to which session.)

$\mathsf {ExtrFail}$ denotes the following event: in some session $sid$, Bob accepts the opening phase (i.e., Bob accepts the proof $\mathrm {SWIA}_{ com }$) with opened message m, and there either is no $sid$-valid pair $(\tilde{m},\tilde{u})$ in $sigqueries$, or the first $sid$-valid pair $(\tilde{m},\tilde{u})$ in $sigqueries$ has $\tilde{m}\ne m$.

Assuming that $\mathsf {ExtrFail}$ occurs only with negligible probability in the real model, then we can easily construct a simulator $\mathrm {Sim}$ for the ideal model. $\mathrm {Sim}$ simulates $\mathrm {Adv}$, Bob and $\mathcal F_\mathrm {SC}$ internally. The communication between $\mathrm {Adv}$ and the environment is forwarded by $\mathrm {Sim}$. When B outputs $\mathtt {committed}$, the simulator looks for the first $sid$-valid pair $(m',u)$ in $sigqueries$ and sends $(\mathtt {commit},m')$ to $\mathcal F_\mathrm {COM}$.

By construction of $\mathrm {Sim}$, we immediately have that the real model and the ideal model are trace-indistinguishable if $\mathsf {ExtrFail}$ occurs with negligible probability in the real model.

Thus, all we have to show is that $\Pr [\mathsf {ExtrFail}]$ is negligible in the following game.

Game 11

An execution of the real model as in Fig. 8a. $\square$

To bound $\Pr [\mathsf {ExtrFail}:Game~11]$, we again construct a sequence of games.

Game 12

Like Game 11, except that in step S5, Bob computes $\sigma _\mathtt {msg1}\leftarrow \mathrm {Sign}( sk ,\mathtt {msg1})$ using the secret key $sk$ of $\mathcal F_\mathrm {SC}$ and then uses $(0,\sigma _\mathtt {msg1})$ as witness for the $\mathrm {WIAOK}_{ ct }$. $\square$

Notice that in this game, Bob is not a valid protocol machine because her behavior depends on $sk$ which is a local variable of $\mathcal F_\mathrm {SC}$. It is, however, not necessary that Game 12 is a valid protocol execution in our model as long as it is well-defined.

Since $\mathrm {WIAOK}_{ ct }$ is quantum-computationally witness-indistinguishable, and both the witness $(u_k,0)$ used by the Bob in Game 11 as well as the witness $(0,\sigma _\mathtt {msg1})$ used by Bob in Game 12 are valid witnesses with respect to $R_{ ct }$ for the statement $( pk ,c_k,k_0)$, we have that $\bigl |\Pr [\mathsf {ExtrFail}:Game~11]- \Pr [\mathsf {ExtrFail}:Game~12]\bigr |$ is negligible.

Game 13

Like Game 12, except that in step S2, Bob executes $(c_k,u_k)\leftarrow \mathrm {COMB}_{B,A}(1^\eta ,0)$ instead of $(c_k,u_k)\leftarrow \mathrm {COMB}_{B,A}(1^\eta ,k_0)$. $\square$

Since the commitment $\mathrm {COMB}$ is quantum-computationally hiding, and its opening information $u_k$ is never used (we removed it from the witness of the $\mathrm {WIAOK}_{ ct }$ in Game 12), we have that $\bigl |\Pr [\mathsf {ExtrFail}:Game~12] - \Pr [\mathsf {ExtrFail}:Game~13]\bigr |$ is negligible.

Game 14

Like Game 13, except that instead of choosing $k_0\in CRS$ already in step S1, Bob chooses $k_0$ only in step S4 as follows: he chooses $crs '\in CRS$ uniformly at random and computes $k_0:= crs '*k_1^{-1}$ where $k_1^{-1}$ is the inverse of $k_1$ with respect to the group operation $*$. $\square$

Since $*$ is a group operation on $CRS$, $k_0:= crs '*k_1^{-1}$ has the same distribution as a uniformly chosen $k_0\in CRS$. Hence $\bigl |\Pr [\mathsf {ExtrFail}:Game~13]- \Pr [\mathsf {ExtrFail}:Game~14]\bigr |$ is negligible (a negligible error may be introduced if we can only efficiently pick elements from $CRS$ with almost uniform distribution).

Notice that the value $crs =k_0*k_1$ that is computed in step S6 equals the value $crs '$ chosen by Bob in step S4.

Game 15

Like Game 14, except that in step S4, instead of choosing $crs '\in CRS$ uniformly, Bob computes $( crs ', td )\leftarrow \mathrm {COMFakeCRS}(1^\eta )$.

Furthermore, in each session, after getting $c_\sigma$ and $c_ sk$ in step C3, Bob computes $(\sigma ^*,m^*,u^*_m):=\mathrm {COMXExtract}( td ,c_\sigma )$ and $sk ^* := \mathrm {COMXExtract}( td ,c_ sk )$. $\square$

The fake CRS property of dual-mode commitments (Definition 22) implies that $crs$ as chosen in Game 14 and in Game 15 are quantum-computationally indistinguishable. (Since $\sigma ^*,m^*,u^*_m, sk ^*$ are never used, the fact that Bob additionally computes these values has no effect.) Hence, $\bigl |\Pr [\mathsf {ExtrFail}:Game~14]- \Pr [\mathsf {ExtrFail}:Game~15]\bigr |$ is negligible.

Summarizing, we have that $|\Pr [\mathsf {ExtrFail}:Game~11]-\Pr [\mathsf {ExtrFail}:Game~ 15]|$ is negligible. Thus, to show that $\Pr [\mathsf {ExtrFail}:Game~11]$ is negligible (which then concludes the proof), we have to show that $\Pr [\mathsf {ExtrFail}:Game~15]$ is negligible.

For the remainder of the proof, all probabilities refer to Game 15, e.g., $\Pr [\mathsf {ExtrFail}]$ means $\Pr [\mathsf {ExtrFail}:Game~15]$.

We define the following events:

• $\mathsf {UnsoundSWIAcom}$: the statement proven in the $\mathrm {SWIA}_{ com }$ is not true. More precisely, in some session $sid$, Bob accepts an execution of $\mathrm {SWIA}_{ com }$ in step O2 with statement $s:=( crs , pk ,c_m,c_\sigma ,s_ sk ,m)$ such that no witness w with $(s,w)\in R_{ com }$ exists.

• $\mathsf {ExtractSK}$: Bob extracts a valid secret key $c_ sk$. Formally, in some session $sid$, $\mathrm {matchingKeys}( pk , sk ^*)=1$.

• $\mathsf {SigForge}$: Bob extracts a forged signature from $c_\sigma$. More precisely, in some session $sid$, $\mathrm {Verify}( pk ,\sigma ^*,(m^*,u^*))=1$ and $(m^*,u^*)\notin sigqueries$.

• $\mathsf {COMHBreak}$: for some session id $sid$, there are two $sid$-valid pairs $(m_1,u_1),(m_2,u_2)\in sigqueries$ with $m_1\ne m_2$.

• $\mathsf {COMXWrongExtr}$ : the commitment $c_\sigma$ or $c_ sk$ can be opened to a value different from what Bob extracted. More precisely, in some session $sid$, there exist $\tilde{u},\tilde{m}$ such that (a) $\mathrm {COMXVerify}( crs ,c_\sigma ,\tilde{m},\tilde{u})=1$ and $\tilde{m}\ne (\sigma ^*,m^*,u^*_m)$ or (b) $\mathrm {COMXVerify}( crs ,c_ sk ,\tilde{m},\tilde{u})=1$ and $\tilde{m}\ne sk ^*$.

The event $\mathsf {UnsoundSWIAcom}$ occurs only with negligible probability since $\mathrm {SWIA}_{ com }$ is a quantum argument.

If $\mathrm {matchingKeys}( pk , sk ^*)=1$, $sk ^*$ could be used to produce arbitrary signatures (that pass verification with respect to $pk$). This contradicts the quantum unforgeability of $\mathfrak S$. Thus, $\mathsf {ExtractSK}$ occurs only with negligible probability.

In Game 15, the secret key $sk$ of $\mathcal F_\mathrm {SC}$ is only used to sign the messages sent to $\mathcal F_\mathrm {SC}$ and to sign the message $\mathtt {msg1}$. Thus, if $\mathsf {SigForge}$ occurs, a signature of a message $(m^*,u^*)$ has been produced that was never honestly signed (we have $(m^*,u^*)\ne \texttt {msg1}$ since $\texttt {msg1}$ is distinct from any pair). Since $\mathfrak S$ is quantum existentially unforgeable, this happens only with negligible probability. Hence, $\mathsf {SigForge}$ occurs with negligible probability.

By definition of $sid$-valid pairs, $(m_1,u_1),(m_2,u_2)\in sigqueries$ with $m_1\ne m_2$ contradicts the quantum-computational binding property of $\mathrm {COMH}$. Thus, $\mathsf {COMHBreak}$ has negligible probability.

Since $(\sigma ^*,m^*,u^*_m)=\mathrm {COMXExtract}( td ,c_\sigma )$, and $sk ^* = \mathrm {COMXExtract}( td ,c_ sk )$, and $( crs ', td )= \mathrm {COMFakeCRS}(1^\eta )$, and $crs '= crs$, we have that the extractability of $\mathrm {COMX}$ (as defined in Definition 22) implies that $\mathsf {COMXWrongExtr}$ has negligible probability.

We proceed to show that in any execution, the following holds:

$$\begin{aligned}&\lnot \mathsf {UnsoundSWIAcom}\wedge \lnot \mathsf {ExtractSK}\wedge \lnot \mathsf {SigForge}\nonumber \\&\quad \wedge \lnot \mathsf {COMHBreak}\wedge \lnot \mathsf {COMXWrongExtr}\Longrightarrow \lnot \mathsf {ExtrFail}\end{aligned}$$

(5)

To show (5), assume an execution in which $\lnot \mathsf {UnsoundSWIAcom}$, $\lnot \mathsf {ExtractSK}$, $\lnot \mathsf {SigForge}$, $\lnot \mathsf {COMHBreak}$, and $\lnot \mathsf {COMXWrongExtr}$ hold. Fix some session $sid$. Let $\mathsf {ExtrFail}_ sid$ denote the event that $\mathsf {ExtrFail}$ occurs in session $sid$. If the $\mathrm {SWIA}_{ com }$ from session $sid$ is not accepted by Bob, we trivially have $\lnot \mathsf {ExtrFail}_ sid$. Thus, we can assume that the $\mathrm {SWIA}_{ com }$ is accepted by Bob. By definition of $R_{ com }$, $\lnot \mathsf {UnsoundSWIAcom}$ then implies that one of the following holds:

• (a) There are values $\sigma ,u_m,u_\sigma$ such that $\mathrm {COMHVerify}(c_m,m,u_m)=1$ and $\mathrm {COMXVerify}( crs ,c_\sigma ,(\sigma ,m,u_m),u_\sigma )=1$ and $\mathrm {Verify}( pk ,\sigma ,(m,u_m))=1$.

• (b) There are values $sk ,u_ sk$ such that $\mathrm {COMXVerify}(c_{ sk }, sk ,u_{ sk })=1$ and $\mathrm {matchingKeys}( pk , sk )=1$.

Since we have $\lnot \mathsf {COMXWrongExtr}$, this implies that one of the following holds:

• (a’) $m=m^*$ and $\mathrm {COMHVerify}(c_m,m^*,u_m^*)=1$ and $\mathrm {Verify}( pk ,\sigma ^*,(m^*,u_m^*))=1$.

• (b’) $\mathrm {matchingKeys}( pk , sk ^*)=1$.

Case (b’) would contradict $\lnot \mathsf {ExtractSK}$. Hence we have $\mathrm {COMHVerify}(c_m,m^*,u_m^*)=1$ and $\mathrm {Verify}( pk ,\sigma ^*,(m^*,u_m^*))=1$. Since $\lnot \mathsf {SigForge}$ holds, $\mathrm {Verify}( pk ,\sigma ^*,(m^*,u_m^*))=1$ implies $(m^*,u_m^*)\in sigqueries$. $\mathrm {COMHVerify}(c_m,m^*,u_m^*)=1$ implies that $(m^*,u_m^*)$ is $sid$-valid. Then, since $\lnot \mathsf {COMHBreak}$, there is no $sid$-valid pair $(m_2,u_2)\in sigqueries$ with $m^*\ne m_2$. Thus, there is a $sid$-valid pair $(\tilde{m},\tilde{u})$ in $sigqueries$, and the first such pair satisfies $\tilde{m}=m^*=m$. Hence, we have $\lnot \mathsf {ExtrFail}_ sid$. Since this holds for any session $sid$, we have shown (5).

Since $\mathsf {UnsoundSWIAcom}$, $\mathsf {ExtractSK}$, $\mathsf {SigForge}$, $\mathsf {COMHBreak}$, and $\mathsf {COMXWrongExtr}$ happen with negligible probability, by (5) $\mathsf {ExtrFail}$ occurs with negligible probability. As shown above, this implies that the real and the ideal models are trace-indistinguishable. Hence, $\pi$ eqUC emulates $(\mathcal F_\mathrm {COM}^{A\rightarrow B,\ell })^*$ in the case of corrupted Alice.

6.2 Two-Party Computation

Corollary 4

(Everlasting two-party computation) Let A and B be parties. Let $\mathcal G$ be a well-formed¹³ classical probabilistic-polynomial-time functionality involving A and B. Under the conditions from Theorem 6, there is a protocol $\pi _{\mathcal G}$ using one instance of $\mathcal F_\mathrm {SC}^{A,\mathfrak S}$ such that $\pi _\mathcal G$ eqUC emulates $\mathcal G^*$.

Proof

In [22], it is shown that there is a classical protocol using polynomially many instances of $\mathcal F_\mathrm {OT}^{A\rightarrow B,1}$ and $\mathcal F_\mathrm {OT}^{B\rightarrow A,1}$ that statistically classical-UC emulates $\mathcal G^*$.

In [39], it is shown that there is a classical protocol using one instance of $\mathcal F_\mathrm {OT}^{B\rightarrow A,1}$ that statistically classical-UC emulates $\mathcal F_\mathrm {OT}^{A\rightarrow B,1}$ (OT reversal).

By composing the protocols from [22] and [39], we get a protocol $\pi _1$ that uses polynomially many instances of $\mathcal F_\mathrm {OT}^{B\rightarrow A,1}$ and statistically classical-UC emulates $\mathcal G^*$.

In [34] it is shown that statistical classical-UC-security implies statistical quantum-UC-security. Thus, $\pi _1$ statistical quantum-UC emulates $\mathcal G^*$.

In [34], it is shown that there is a protocol using polynomially many instances of $\mathcal F_\mathrm {COM}^{A\rightarrow B}$ that statistically quantum-UC emulates $\mathcal F_\mathrm {OT}^{B\rightarrow A,1}$.

By composing $\pi _1$ and the protocol from [34], we get a protocol $\pi _2$ that uses $(\mathcal F_\mathrm {COM}^{A\rightarrow B})^*$ and statistically quantum-UC emulates $\mathcal G^*$ and thus eqUC emulates $\mathcal G^*$.

By composing the protocol $\pi _2$ with the protocol from Theorem 6, we get a protocol $\pi$ using a single instance of $\mathcal F_\mathrm {SC}^{A,\mathfrak S}$ and that eqUC emulates $\mathcal G^*$.$\square$

6.3 Improvements & Future Work

• (a) Give protocols for multi-party computation. We have only discussed two-party computation. Corollary 4 can easily be extended to multi-party computation by running an instance of the protocol from Theorem 6 for each pair of parties. But then we end up with a protocol where every party needs one signature card for each communication partner. To get eqUC multi-party computation with only one signature card per party, we need to show that a signature card can be shared between instances of the protocol that run with different communication partners (we have only analyzed the case where it is shared between different instances with the same communication partner). We foresee no difficulties, but the analysis becomes somewhat more complex because one needs to make sure that the argument of knowledge from the setup phase (Step S5) in one instance does not run concurrently with the signing in the commit phase (Step C2) of another instance—otherwise we will again have the problem that we rewind a prover that accesses the signing oracle.

• (b) With our protocol, the signature card must be used exclusively by our protocol. No guarantees are made if the same signature card is used in other protocols. For example, if we wish to implement the secure channels in the two-party computation protocol using the QKD-based protocol from Corollary 3, we end up with a protocol that needs two signature cards for Alice instead of one. Also, in many cases a user cannot get several signature cards (for example if the signature card is part of his national ID document).

  To cope with these cases, we need to make sure that the protocol stays secure even if the signature card is also used by other protocols. This can be achieved by adapting the GUC model [9] to the everlasting quantum-UC case. In the GUC model (or equivalently UC with catalysts [21]), the trusted setup used by the protocol (the signature card in our case) can concurrently be accessed by other protocols. Of course, our protocol immediately becomes insecure in this case. For example, Bob might obtain a signature on $\mathtt {msg1}$ through some other protocol and use this to cheat in the setup phase. This can be avoided by not using a fixed message $\mathtt {msg1}$ but letting Alice choose what message $m_1$ is to be signed instead. And additionally we need to make sure that Bob cannot obtain a signature on $m_1$ after Alice announces $m_1$. This can be achieved by using the locking approach from [21]: they show how to get GUC-security with signature cards by implementing a locking mechanism that restricts access by other protocol instances in critical protocol steps. (In our case, the lock would need to be in place starting from the point where Alice announces $m_1$ till the end of the proof in Step S5.)

  Notice that this approach will also immediately solve the problem described in (a): the GUC composition theorem allows us to share the same signature card between different instances of the protocol, even when they run with different communication partners.

• (c) Can the original protocol from [27] be shown secure in the quantum setting? Perhaps any quantum unforgeable signature scheme is still unforgeable when the adversary is given access to the inverse of the signing oracle?