Tightly Secure Signatures From Lossy Identification Schemes

Abstract

In this paper, we present three digital signature schemes with tight security reductions in the random oracle model. Our first signature scheme is a particularly efficient version of the short exponent discrete log-based scheme of Girault et al. (J Cryptol 19(4):463–487, 2006). Our scheme has a tight reduction to the decisional short discrete logarithm problem, while still maintaining the non-tight reduction to the computational version of the problem upon which the original scheme of Girault et al. is based. The second signature scheme we construct is a modification of the scheme of Lyubashevsky (Advances in Cryptology—ASIACRYPT 2009, vol 5912 of Lecture Notes in Computer Science, pp 598–616, Tokyo, Japan, December 6–10, 2009. Springer, Berlin, 2009) that is based on the worst-case hardness of the shortest vector problem in ideal lattices. And the third scheme is a very simple signature scheme that is based directly on the hardness of the subset sum problem. We also present a general transformation that converts what we term $lossy$ identification schemes into signature schemes with tight security reductions. We believe that this greatly simplifies the task of constructing and proving the security of such signature schemes.

1 Introduction

Due to the widespread use of digital signature schemes in practical applications, their construction and security analysis comprises an important area of modern cryptography. While there exist many digital signatures that are secure in the standard model (e.g., [7, 8, 12, 19, 29]), they are usually less efficient than those that are proved secure in the random oracle model and so are not as suitable for practical applications. Signature schemes secure in the random oracle model generally fall into one of two categories. In the first category are schemes constructed using the full domain hash (FDH) approach [5], and in the second are schemes based on the Fiat-Shamir technique [16]. Our current work focuses on the latter type.

Proving the security of schemes that are designed using the Fiat-Shamir heuristic (e.g., [26, 28, 51]) generally involves an invocation of the forking lemma [47]. Reductions with this feature entail getting one forgery from the adversary, rewinding him back to a particular point, and then re-running the adversary from that point with the hope of getting another forgery. Using these two related forgeries, the reduction can extract an answer to some underlying hard problem such as discrete log or factorization. Due to the fact that one needs to guess on which of his $q_\mathrm{h}$ random oracle queries the adversary will forge on, a reduction using an adversary that succeeds with probability $\varepsilon$ in forging a signature will have probability $\varepsilon /q_\mathrm{h}$ of breaking the hardness assumption. Asymptotically, this does not cause a problem, since the reduction only incurs a polynomial loss in the success probability. The reduction does not, however, provide us with useful guidance for setting concrete parameters because it is unclear whether the efficiency loss is just an artifact of the proof or whether it represents an actual weakness of the scheme. It is therefore preferable to construct protocols that have a tight proof of security by avoiding the use of the forking lemma.

1.1 Related Work and Contributions

Constructing number-theoretic signature schemes with tight security reductions has received some attention in the past. The first work in this direction is due to Bellare and Rogaway [5], who proposed an RSA-based signature scheme known as PSS whose security is tightly related to the security of the RSA function. Later, in the context of signature schemes based on the Fiat-Shamir heuristic, Micali and Reyzin [43] showed that it is sometimes possible to modify the Fiat-Shamir transform in order to achieve tighter reductions. In more recent work, Goh and Jarecki [21] and Katz and Wang [22, 32] constructed digital signatures with tight security reductions based on the computational and decisional Diffie-Hellman problems. These latter two schemes are versions of the Schnorr signature scheme and thus inherit most of its characteristics. In particular, the scheme based on the DDH problem has a very simple construction and a rather short signature size. There are other signature schemes, though, that possess other desirable features, but do not yet have a tight security reduction. A notable example of such a scheme is the one of Girault, Poupard, and Stern [26], which is extremely efficient when the signer is allowed to perform preprocessing before receiving the signature. One of the contributions of this paper is a construction of a scheme that possesses all the advantages of the scheme in [26] in addition to having a tight security reduction.

As far as we are aware, there has not been any previous work that specifically considered tight reductions for lattice-based signatures. Similar to number-theoretic constructions, lattice-based signatures secure in the random oracle model are built using either the full domain hash [27, 42, 55] or the Fiat-Shamir [31, 37–39, 44] methodologies. While FDH-based lattice signatures have tight reductions, the currently most efficient lattice-based schemes (in terms of both the signature size and the running time) are those based on the Fiat-Shamir framework [38, 39]. And so it is an interesting problem whether it is possible to construct an efficient Fiat-Shamir-based scheme that has tight reductions. The construction of such a scheme is another contribution of this work, though it is unfortunately a little less efficient than the ones in [38, 39].

The third scheme that we construct in our work is based on the hardness of the low-density subset sum problem. Due to a known reduction from subset sum to lattice problems [15, 34], all signature schemes based on lattices are already based on subset sum. The aforementioned reduction, however, incurs a loss, and so, the lattice-based schemes are not based on as hard a version of subset sum as we achieve in this paper by building a scheme directly on subset sum. Additionally, our scheme is surprisingly simple (to describe and to prove), and we believe that it could be of theoretical interest.

Proving schemes secure using the Fiat-Shamir heuristic is usually done by first building a three-move identification scheme secure against passive adversaries and then applying the Fiat-Shamir transformation, which was proven in [1] to yield provably secure signatures. The advantage of building schemes using this modular approach is that one does not have to deal with any (usually messy) issues pertaining to random oracles when building the identification scheme—all mention of random oracles is delegated to the black-box transformation. For signature schemes with tight security reductions, however, this construction method does not work. The reason is that the transformation of [1] inherently loses a factor of $q_\mathrm{h}$ in the success probability of the impersonator to the ID scheme in relation to the forger of the signature scheme, which results in a non-tight security reduction.

In this paper, we give a black-box transformation analogous to that of [1] that converts what we call, lossy identification schemes into signature schemes with tight security reductions. Roughly speaking, a lossy identification scheme is a three-move commit-challenge-response identification scheme that satisfies the following four simple properties:

• 1. Completeness: The verification algorithm must accept a valid interaction with non-negligible probability.

• 2. Simulatability: There is a simulator, who does not have access to the secret key, who is able to produce valid interaction transcripts that are statistically indistinguishable from real ones.

• 3. Key-indistinguishability: There is an algorithm that produces lossy keys that are computationally indistinguishable from the real keys.

• 4. Lossiness: When the keys are lossy, it is statistically impossible to provide a valid response to a random challenge after making a commitment.

Properties 1 and 2 are generally true of all identification schemes, whereas properties 3 and 4 are particular to the lossy case and are crucially required for obtaining a tight black-box transformation. Our transformation converts a lossy identification scheme into a signature scheme and proves that a successful forger can be converted into a successful impersonator to the identification scheme. Since the only non-statistical property in the definition above is property 3, it means that the successful impersonator breaks this property, which is where we will plant the instance of the hard problem that we are trying to solve. We demonstrate the usefulness and generality of this approach by building our signature schemes in this way.

1.2 Overview of Our Signature Schemes

1.2.1 Construction Based on the (Decisional) Short Discrete Logarithm Problem

The (computational) $c$-discrete logarithm with short exponent ($c$-DLSE) problem in a cyclic group ${\mathbb {G}}$ with generator $g$ is the well-studied problem of recovering the discrete logarithm $x$ of a given group element $g^x$ when $x$ is a $c$-bit long integer, $c$ being typically much smaller than the bit-size of ${\mathbb {G}}$. Pollard’s kangaroo algorithm [48] solves this problem in time $O(2^{c/2})$, but when ${\mathbb {G}}$ is a subgroup of prime order in $\mathbb {Z}_p^*$ and $c$ is at least twice the security parameter ($c=160$ for the $80$-bit security level, say), the $c$-DLSE problem is believed to be as hard as the full-length discrete logarithm problem [45, 56]. A number of cryptographic schemes are based on the hardness of the $c$-DLSE problem, including pseudorandom bit generators [17, 18, 45], key agreement protocols [23] and signature schemes including Girault–Poupard–Stern (GPS) signatures [26, 49].

Like other discrete log-based schemes [9, 32, 51], GPS is an online/offline scheme in the sense of Even, Goldreich and Micali [13, 14]: When preprocessing can be done prior to receiving the message to be signed, signature generation becomes very efficient. The main advantage of GPS signatures, however, is that this online signature generation step does not even require a modular reduction, which according to the work of [52] can save as much as 60 % of the signing time, which makes the scheme extremely well suited for situations where processing time is at a premium.

Our scheme, described in Sect. 4, is very similar to the scheme of [26], but with some tweaks making it possible to choose smaller parameters. Moreover, while the security proof for GPS is a very loose reduction to the computational $c$-DLSE problem, our security proof provides a tight reduction, which is, however, to the decisional short discrete log problem ($c$-DSDL). Informally, the $c$-DSDL problem asks to distinguish between a pair $(g,g^x)$ where $x$ is $c$-bit long and a pair $(g,h)$ where $h$ is uniformly random. No better algorithm is known for solving this problem than actually computing the discrete logarithm and checking whether it is small—in fact, a search-to-decision reduction was established by Koshiba and Kurosawa [33].

Given the pair $(g,g^x)$, we set it as the public key, which by our assumption is computationally indistinguishable from $(g,g^x)$ where $x$ is random (i.e., not small). We then build an identification scheme that satisfies our simulatability requirement and furthermore show that it is information-theoretically impossible to respond to a random challenge if $x$ is not small. Using our transformation to signatures, this implies that if a forger can produce a valid forgery, then he can respond to a random challenge, which would mean that $x$ is small.

In the end, we obtain a tightly secure scheme which is quite efficient in terms of size (signatures are around $320$-bits long at the $80$-bit security level) and speed, especially when used with coupons (in which case, signature generation only requires a single multiplication between integers of $80$ and $160$ bits, respectively).

1.2.2 Construction Based on the Shortest Vector Problem in Ideal Lattices

In Section 5, we give a construction of a signature scheme based on the hardness of the approximate worst-case shortest vector problem in ideal lattices. Our scheme is a modification of the scheme in [38] that eliminates the need to use the forking lemma. The scheme in [38] was shown to be secure based on the hardness of the $\text{ Ring-SIS }$ problem, which was previously shown to be as hard as worst-case ideal lattice problems [35, 46]. In this work, we construct a similar scheme, but instead have it based on the hardness of the $\text{ Ring-LWE }$ problem, which was recently shown to also be as hard as the worst-case shortest vector problem under quantum reductions [36].

The secret key in our scheme consists of two vectors $\mathbf{s}_1,\mathbf{s}_2$ with small coefficients in the ring $\mathcal {R}=\mathbb {Z}_q[\mathbf{x}]/(\mathbf{x}^n+1)$, and the public key consists of a random element $\mathbf{a}\in \mathcal {R}^\times$ and $\mathbf{t}=\mathbf{a}\mathbf{s}_1+\mathbf{s}_2$. The $\text{ Ring-LWE }$ reduction states that distinguishing $(\mathbf{a},\mathbf{t})$ from a uniformly random pair in $\mathcal {R}^\times \times \mathcal {R}$ is as hard as solving worst-case lattice problems. In our identification scheme, the commitment is the polynomial $\mathbf{a}\mathbf{y}_1+\mathbf{y}_2$ where $\mathbf{y}_1,\mathbf{y}_2$ are elements in $\mathcal {R}$ chosen with a particular distribution. The challenge is an element $\mathbf{c}\in \mathcal {R}$ with small coefficients, and the response is $(\mathbf{z}_1,\mathbf{z}_2)$ where $\mathbf{z}_1=\mathbf{y}_1+\mathbf{s}_1\mathbf{c}$ and $\mathbf{z}_2=\mathbf{y}_2+\mathbf{s}_2\mathbf{c}$. As in [38], the procedure sometimes aborts in order to make sure that the distribution of $(\mathbf{z}_1,\mathbf{z}_2)$ is independent of the secret keys. The verification procedure checks that $\mathbf{z}_1,\mathbf{z}_2$ have “small” coefficients and that $\mathbf{a}\mathbf{z}_1+\mathbf{z}_2-\mathbf{c}\mathbf{t}=\mathbf{a}\mathbf{y}_1+\mathbf{y}_2$.

The crux of the security proof lies in showing that whenever $(\mathbf{a},\mathbf{t})$ is truly random, it is information-theoretically impossible to produce a valid response to a random challenge. Proving this part in our security reduction requires analyzing the ideal structure of the ring $\mathcal {R}$ using techniques similar to the ones in [40]. This analysis is somewhat loose, however, so that the resulting signature scheme is not as efficient as the one in [38]. We believe that improving the analysis (possibly using some recent techniques in [53]) and obtaining a more efficient signature scheme is an interesting research direction.

1.2.3 Construction Based on Subset Sum

In Section 6, we present a very simple scheme based on the hardness of the subset sum problem. The secret key consists of a matrix $\mathbf{X}\in \{0,1\}^{n\times k}$, and the public key consists of a random vector $\mathbf{a}\in \mathbb {Z}_M^n$, as well as a $k$-dimensional vector of subset sums $\mathbf{t}=\mathbf{a}^T\mathbf{X}\mod M$ that use $\mathbf{a}$ as weights. The main idea for constructing the lossy identification scheme is to achieve the property that if the vector $\mathbf{t}$ is uniformly random, rather than being a vector of valid subset sums, then it should be impossible (except with a small probability) to produce a valid response to a random challenge. And so an adversary who is able to break the resulting signature scheme can be used to distinguish vectors $\mathbf{t}$ that are valid subset sums of the elements in $\mathbf{a}$ from those that are just uniformly random. We defer further details to Sect. 6.

2 Preliminaries

2.1 The Decisional Short Discrete Logarithm Problem

Let ${\mathbb {G}}$ be a finite, cyclic group of prime order $q$ whose group operation is noted multiplicatively, and $g$ a fixed generator of ${\mathbb {G}}$. Let further $c$ be a size parameter. The $c$-decisional discrete logarithm ($c$-DSDL) problem may be informally described as the problem of distinguishing between tuples of the form $(g,h)$ for a uniformly random $h\in {\mathbb {G}}$ and tuples of the form $(g,g^x)$ with $x$ uniformly random in $\{0,\dots ,2^c-1\}$. More precisely:

Definition 1

A distinguishing algorithm $\fancyscript{D}$ is said to $(t,\varepsilon )$-solve the $c$-DSDL problem in group ${\mathbb {G}}$ if $\fancyscript{D}$ runs in time at most $t$ and satisfies:

$$\begin{aligned} \big | \Pr \left[ x\overset{\$}{\leftarrow }\mathbb {Z}_q : \fancyscript{D}(g,g^x)=1\right] - \Pr \left[ x\overset{\$}{\leftarrow }\{0,\dots ,2^c-1\} : \fancyscript{D}(g,g^x)=1\right] \big | \ge \varepsilon \end{aligned}$$

We say that ${\mathbb {G}}$ is a $(t,\varepsilon )$-$c$-DSDL group if no algorithm $(t,\varepsilon )$-solves the $c$-DSDL problem in ${\mathbb {G}}$.

This problem is related to the well-known (computational) $c$-discrete logarithm with short exponent ($c$-DLSE) problem. In fact, for the groups where that problem is usually considered, namely prime-order subgroups of $\mathbb {Z}_p^*$ where $p$ is a safe prime, a search-to-decision reduction is known for all $c$ [33]: If the $c$-DLSE problem is hard, then so is the $c$-DSDL problem. The reduction is not tight, however, so while the signature scheme presented in Sect. 4 admits a tight reduction to the decisional problem, there is a polynomial loss in the reduction to the search problem.

2.2 The Ring-LWE Problem and Lattices

For any positive integer $n$ and any positive real $\sigma$, the distribution $D_{\mathbb {Z}^n,\sigma }$ assigns the probability proportional to $e^{-\pi \Vert \mathbf{y}\Vert ^2/\sigma ^2}$ to every $\mathbf{y}\in \mathbb {Z}^n$ and $0$ everywhere else. For any odd prime $p$, the ring $\mathcal {R}=\mathbb {Z}_p[\mathbf{x}]/(\mathbf{x}^n+1)$ is represented by polynomials of degree at most $n-1$ with coefficients in the range $\left[ -\frac{p-1}{2},\frac{p-1}{2}\right]$. As an additive group, $\mathcal {R}$ is isomorphic to $\mathbb {Z}_p^n$, and we use the notation $\mathbf{y}\overset{\$}{\leftarrow }D_{\mathcal {R},\sigma }$ to mean that a vector $\mathbf{y}$ is chosen from the distribution $D_{\mathbb {Z}^n,\sigma }$ and then mapped to a polynomial in $\mathcal {R}$ in the natural way (i.e., position $i$ of the vector corresponds to the coefficient of the $\mathbf{x}^i$ term of the polynomial).

The (decisional) ring learning with errors problem $(\text{ Ring-LWE })$ over the ring $\mathcal {R}$ with standard deviation $\sigma$ is to distinguish between the following two oracles: $\mathcal {O}_0$ outputs random elements in $\mathcal {R}\times \mathcal {R}$, while the oracle $\mathcal {O}_1$ has a secret $\mathbf{s}\in \mathcal {R}$ where $\mathbf{s}\overset{\$}{\leftarrow }D_{\mathcal {R},\sigma }$, and on every query, it chooses a uniformly random element $\mathbf{a}\overset{\$}{\leftarrow }\mathcal {R}, \mathbf{e}\overset{\$}{\leftarrow }D_{\mathcal {R},\sigma }$, and outputs $(\mathbf{a},\mathbf{a}\mathbf{s}+\mathbf{e})$. The $\text{ Ring-LWE }$ problem is a natural generalization of the $\text{ LWE }$ problem [50] to rings, and it was recently shown in [36] that if $p=\hbox {poly}(n)$ is a prime congruent to $1\mod 2n$, then solving the $\text{ Ring-LWE }$ problem over the ring $\mathcal {R}$ with standard deviation¹ $\sigma$ is as hard as finding an approximate shortest vector in all ideal lattices in the ring $\mathbb {Z}[\mathbf{x}]/(\mathbf{x}^n+1)$. Intuitively, the smaller the ratio between $p$ and $\sigma$ is, the smaller the vector the reduction is able to find, and thus, it is preferable to keep this ratio low.

Note also that for such a choice of parameters ($p\equiv 1\mod 2n$, which implies in particular $p = \varOmega (n)$ and $\mathcal {R}\cong \mathbb {Z}_p^n$), the $\text{ Ring-LWE }$ problem as defined above is equivalent to the same decisional problem, but where the element $\mathbf{a}$ is chosen as a uniformly random invertible element of $\mathcal {R}$ instead, and the adversary has to distinguish $(\mathbf{a},\mathbf{a}\mathbf{s}+\mathbf{e})$ from a uniformly random element of $\mathcal {R}^\times \times \mathcal {R}$. This is because the fraction $(1-1/p)^n$ of elements of $\mathcal {R}$ which are invertible is constant. In this paper, we will refer to both equivalent variants of the problem as $\text{ Ring-LWE }$.

2.3 The Subset Sum Problem

In the search version of the modular random subset sum problem, $\text{ SS }(n,M)$, one is given $n$ elements $a_i$ generated uniformly at random in $\mathbb {Z}_M$ (in this paper, we will only deal with low-density instances of the problem, where $M>2^n$) and an element $t=\sum {a_is_i} \mod M$, where the $s_i$ are randomly chosen from $\{0,1\}$, and is asked to find the $s_i$ (with high probability, there is only one possible set of $s_i$). The decision version of the problem, which was shown to be as hard as the search version [30, 41], is to distinguish an instance $(a_1,\ldots ,a_n,t)$ where $t=a_1x_1+\cdots +a_ns_n \mod M$ from the instance $(a_1,\ldots ,a_n,t)$ where $t$ is uniformly random in $\mathbb {Z}_M$. The low-density $\text{ SS }(n,M)$ problem is hardest when $M\approx 2^n$, in which case the best algorithm runs in time $2^{\varOmega (n)}$ (see for example [3]), but the best-known algorithms for the problem, when $M=n^{O(n)}$, still require time $2^{\varOmega (n)}$. As $M$ increases, however, the problem becomes easier, until it is solvable in polynomial time when $M=2^{\varOmega (n^2)}$ [15, 34].

2.4 Signature Schemes

Definition 2

A signature scheme $\mathsf {Sig}$ is composed of three probabilistic polynomial-time algorithms $({\mathsf {KeyGen}},{\mathsf {Sign}},{\mathsf {Verify}})$ such that:

• The key generation algorithm ${\mathsf {KeyGen}}$ takes as input the security parameter in unary notation and outputs a pair $(pk,sk)$ containing the public verification key and the secret signing key.

• The signing algorithm ${\mathsf {Sign}}$ takes as input a message $m$ and the signing key $sk$ and outputs a signature $\sigma$. This algorithm can be probabilistic so that many signatures can be computed for the same message.

• The verification algorithm ${\mathsf {Verify}}$ takes as input a message $m$, a signature $\sigma$ and the public key $pk$ and outputs $1$ if the signature is correct and $0$ otherwise.

The standard security notion for signature scheme is existential unforgeability against adaptive chosen-message attacks [24], which informally means that, after obtaining signatures on polynomially many arbitrary messages of his choice, an adversary cannot produce a valid signature for a new message.

Definition 3

Let $\mathsf {Sig}= ({\mathsf {KeyGen}},{\mathsf {Sign}},{\mathsf {Verify}})$ be a signature scheme and let $H$ be a random oracle. We say that $\mathsf {Sig}$ is $(t,q_h,q_s,\varepsilon )$-existentially unforgeable against adaptive chosen-message attacks, if there is no algorithm $\mathcal {F}$ that runs in time at most $t$, while making at most $q_h$ hash queries and at most $q_s$ signing queries, such that

$$\begin{aligned}&\Pr [(pk,sk)\leftarrow {\mathsf {KeyGen}}(1^k); (m,\sigma )\leftarrow \mathcal {F}^{{\mathsf {Sign}}(sk,\cdot ),H(\cdot )}(pk):\\&\quad m \notin {\mathcal {S}} \wedge {\mathsf {Verify}}(m,\sigma ,pk)=1] \ge \varepsilon , \end{aligned}$$

where ${\mathcal {S}}$ is the set of messages queried to the signing oracle.

Furthermore, we say that a signature scheme satisfies strong existential unforgeability against adaptive chosen-message attacks if, after obtaining signatures on polynomially many arbitrary messages of his choice, an adversary cannot produce a new valid signature, even for a message $m$ for which he already knows a correct signature.

Definition 4

Let $\mathsf {Sig}= ({\mathsf {KeyGen}},{\mathsf {Sign}},{\mathsf {Verify}})$ be a signature scheme and let $H$ be a random oracle. We say that $\mathsf {Sig}$ is $(t,q_h,q_s,\varepsilon )$ strongly existentially unforgeable against adaptive chosen-message attacks, if there is no algorithm $\mathcal {F}$ that runs in time at most $t$, while making at most $q_h$ hash queries and at most $q_s$ signing queries, such that

$$\begin{aligned}&\Pr [(pk,sk)\leftarrow {\mathsf {KeyGen}}(1^k); (m,\sigma )\leftarrow \mathcal {F}^{{\mathsf {Sign}}(sk,\cdot ),H(\cdot )}(pk):\\&\quad (m,\sigma )\notin {\mathcal {S}} \wedge {\mathsf {Verify}}(m,\sigma ,pk)=1] \ge \varepsilon , \end{aligned}$$

where ${\mathcal {S}}$ is the set of message–signature pairs obtained via queries to the signing oracle.

3 Lossy Identification Schemes

In order to unify the security proofs of our signature schemes without sacrificing the tightness of the reduction, we introduce in this section a new class of identification schemes, called lossy identification schemes. In these schemes, the public key associated with the prover can take one of two indistinguishable forms, called normal and lossy. When the public key is normal, the scheme behaves as a standard identification scheme with similar security guarantees against impersonation attacks. However, in the lossy case, the public key may not have a corresponding secret key and no prover (even computationally unbounded ones) should be able to make the verifier accept with non-negligible probability.

As with other identification schemes used to build signature schemes via the Fiat-Shamir transform, the identification schemes that we consider in this paper consist of a canonical three-move protocol, as defined in [1]. In these protocols, the verifier’s move consists in choosing a random string from the challenge space and sending it to the prover. Moreover, its final decision is a deterministic function of the conversation transcript and the public key. Since our results can be seen as a generalization of the results of Abdalla et al. [1] to the lossy setting, we use their definitions as the basis for ours below.

Definition 5

A lossy identification scheme $\mathsf {ID}$ is defined by a tuple $({\mathsf {KeyGen}}, {\mathsf {LosKeyGen}}, {\mathsf {Prove}}, c, {\mathsf {Verify}})$ such that:

• ${\mathsf {KeyGen}}$ is the normal key generation algorithm, which takes as input the security parameter $k$ in unary notation and outputs a pair $(pk,sk)$ containing the publicly available verification key and the prover’s secret key.

• ${\mathsf {LosKeyGen}}$ is the lossy key generation algorithm, which takes as input the security parameter $k$ in unary notation and outputs a lossy verification key $pk$.

• ${\mathsf {Prove}}$ is the prover algorithm, which takes as input the secret key $sk$ and the current conversation transcript and outputs the next message to be sent to the verifier.

• $c(k)$ is a function of the security parameter $k$, which determines the length of the challenge sent by the verifier.

• ${\mathsf {Verify}}$ is a deterministic algorithm, which takes the verification key $pk$ and the conversation transcript as input and outputs $1$ to indicate acceptance or $0$ otherwise.

Following [1], we associate to $\mathsf {ID}, k$, and $(pk,sk)$ a randomized transcript generation oracle $\mathsf {Tr}^{\mathsf {ID}}_{pk,sk,k}$, which takes no inputs and returns a random transcript of an “honest” execution. However, to adapt it to specific setting of our schemes, we modify to the original definition to take into account the possibility that the prover may fail and output $\bot$ as response during the execution of the identification protocol. Moreover, when this happens, instead of returning $(cmt,ch,\bot )$, our transcript generation oracle will simply output a triplet $(\bot ,\bot ,\bot )$ to simulate the scenario in which the verifier simply forgets failed identification attempts. Interestingly, as we show later in this section, this weaker requirement is sufficient for building secure signature schemes as failed impersonation attempts will be kept hidden from the adversary since the tasks of generating the commitment and challenge are performed by the signer. More precisely, the transcript generation oracle $\mathsf {Tr}^{\mathsf {ID}}_{pk,sk,k}$ is defined as follows:

Definition 6

An identification scheme is said to be lossy if it has the following properties:

• 1. Completeness of normal keys. We say that $\mathsf {ID}$ is $\rho$-complete, where $\rho$ is a non-negligible function of $k$, if for every security parameter $k$ and all honestly generated keys $(pk,sk)\overset{\$}{\leftarrow }{\mathsf {KeyGen}}(1^k), {\mathsf {Verify}}(pk,cmt,ch,rsp)=1$ holds with probability $\rho$ when $(cmt,ch,rsp) \overset{\$}{\leftarrow }\mathsf {Tr}^{\mathsf {ID}}_{pk,sk,k}()$.

• 2. Simulatability of transcripts. Let $(pk,sk)$ be the output of ${\mathsf {KeyGen}}(1^k)$ for a security parameter $k$. Then, we say that $\mathsf {ID}$ is $\varepsilon$-simulatable if there exists a PPT algorithm $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk,k}$ with no access to the secret key $sk$ which can generate transcripts $\{(cmt,ch,rsp)\}$ whose distribution is statistically indistinguishable from the transcripts output by $\mathsf {Tr}^{\mathsf {ID}}_{pk,sk,k}$, where $\varepsilon$ is an upper bound for the statistical distance. When $\varepsilon =0$, then $\mathsf {ID}$ is said to be perfectly simulatable.

• 3. Indistinguishability of keys. Consider the experiments $\mathbf {Exp}_{{\mathsf {ID},\fancyscript{D}}}^\mathrm {ind\hbox {-}keys\hbox {-}real}(k)$ and $\mathbf {Exp}_{{\mathsf {ID},\fancyscript{D}}}^\mathrm {ind\hbox {-}keys\hbox {-}lossy}(k)$ in which we generate $pk$ via ${\mathsf {KeyGen}}(1^k)$, respectively ${\mathsf {LosKeyGen}}(1^k)$, and provide it as input to the distinguishing algorithm $\fancyscript{D}$. We say that $\fancyscript{D}$ can $(t,\varepsilon )$-solve the key-indistinguishability problem if $\fancyscript{D}$ runs in time $t$ and

  $$\begin{aligned} \big | {\Pr \left[ \,{\mathbf {Exp}_{{\mathsf {ID},\fancyscript{D}}}^\mathrm {ind\hbox {-}keys\hbox {-}real}(k)=1}\,\right] } - {\Pr \left[ \,{\mathbf {Exp}_{{\mathsf {ID},\fancyscript{D}}}^\mathrm {ind\hbox {-}keys\hbox {-}lossy}(k)=1}\,\right] } \big | \ge \varepsilon . \end{aligned}$$

  Furthermore, we say that $\mathsf {ID}$ is $(t,\varepsilon )$-key-indistinguishable if no algorithm $(t,\varepsilon )$-solves the key-indistinguishability problem.

• 4. Lossiness. Let $\fancyscript{I}$ be an impersonator, $st$ be its state, and $k$ be a security parameter. Let $\mathbf {Exp}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k)$ be the following experiment played between $\fancyscript{I}$ and a hypothetical challenger:

  

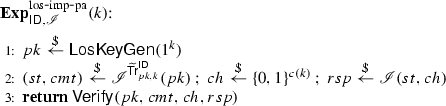
  We say $\fancyscript{I}\varepsilon$-solves the impersonation problem with respect to lossy keys if

  $$\begin{aligned} {\Pr \left[ \,{\mathbf {Exp}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k)=1}\,\right] } \ge \varepsilon . \end{aligned}$$

  Furthermore, we say that $\mathsf {ID}$ is $\varepsilon$-lossy if no (computationally unrestricted) algorithm $\varepsilon$-solves the impersonation problem with respect to lossy keys.

Unlike the definition of identification schemes in [1], our definition of lossy identification schemes does require the scheme to be zero-knowledge and, as such, it can be seen as a special type of honest-verifier zero-knowledge proof [6, 11, 25].

While our new definition could be generalized to consider the case in which the lossy key generation additionally outputs a lossy secret key, as in the case of lossy encryption [4], we opted not to do so for ease of exposition and because none of our instantiations require such generalization.

Moreover, as in [1], we need to use the concept of min-entropy [10] to measure the maximum likelihood that a commitment generated by the prover collides with a fixed value. The precise definition of min-entropy can be found in Definition 3.2 in [1], which is restated in the context of lossy identification schemes in Appendix 2.

In order to prove that a signature scheme obtained via the Fiat-Shamir transform is strongly existentially unforgeable, the underlying identification scheme will need to satisfy an additional property, called uniqueness, which states that, given a valid transcript $(cmt, ch, rsp)$ with respect to a public key $pk$, the probability that there exists a new response value $rsp' \not = rsp$ for which $(cmt, ch, rsp')$ is a valid transcript is negligible.

Definition 7

Let $\mathsf {ID}=({\mathsf {KeyGen}}, {\mathsf {LosKeyGen}}, {\mathsf {Prove}}, c, {\mathsf {Verify}})$ be a lossy identification scheme and let $pk$ be the output of ${\mathsf {LosKeyGen}}(1^k)$ for a security parameter $k$. Let $(cmt, ch, rsp)$ be a valid transcript output by a lossy transcript generation function $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk,k}()$. We say that $\mathsf {ID}$ is $\varepsilon$-unique with respect to lossy keys if the probability that there exists a new response value $rsp' \not = rsp$ for which ${\mathsf {Verify}}(pk, cmt, ch, rsp') = 1$ is at most $\varepsilon$, and perfectly unique if no such response value exists at all.

3.1 Transform

The signature schemes that we consider in this paper are built from lossy identification schemes via the Fiat-Shamir transform [16], in which the challenge becomes the hash of the message together with the commitment. However, since we do not assume perfect completeness of normal keys for the underlying lossy identification scheme, the signing algorithm will differ slightly from those considered in [1] in order to decrease the probability of abort during signing. More precisely, let $\mathsf {ID}=({\mathsf {KeyGen}}, {\mathsf {LosKeyGen}}, {\mathsf {Prove}}, c, {\mathsf {Verify}})$ be a lossy identification scheme and let $H$ be a random oracle. Let $\ell$ be a parameter defining the maximum number of signing attempts. We can construct a signature scheme $\mathsf {Sig}[\mathsf {ID},\ell ]=({\mathsf {KeyGen}},{\mathsf {Sign}},{\mathsf {Verify}})$, as depicted in Fig. 1.

Fig. 1

Description of our signature scheme $\mathsf {Sig}[\mathsf {ID},\ell ]=({\mathsf {KeyGen}},{\mathsf {Sign}},{\mathsf {Verify}})$, where $\mathsf {ID}=({\mathsf {KeyGen}}, {\mathsf {LosKeyGen}}, {\mathsf {Prove}}, c, {\mathsf {Verify}})$ is a lossy identification scheme, $H$ is a random oracle, and $\ell$ is a bound on the number of signing attempts

We remark that the signature length of the scheme in Fig. 1 can sometimes be optimized by setting $\sigma = (ch, rsp)$. However, this is only possible when the commitment value $cmt$ is uniquely defined by $(ch,rsp)$, which is the case for all the schemes considered in this paper.

Theorem 1

Let $\mathsf {ID}=({\mathsf {KeyGen}}, {\mathsf {LosKeyGen}}, {\mathsf {Prove}}, c, {\mathsf {Verify}})$ be a lossy identification scheme whose commitment space has min-entropy $\beta (k)$, let $H$ be a random oracle, and let $\mathsf {Sig}[\mathsf {ID}]= ({\mathsf {KeyGen}}, {\mathsf {Sign}}, {\mathsf {Verify}})$ be the signature scheme obtained via the transform in Fig. 1. If $\mathsf {ID}$ is $\varepsilon _{s}$-simulatable, $\rho$-complete, $(t',\varepsilon _{k})$-key-indistinguishable, and $\varepsilon _{\ell }$-lossy, then $\mathsf {Sig}[\mathsf {ID}]$ is $(t,q_h,q_s,\varepsilon )$-existentially unforgeable against adaptive chosen-message attacks in the random oracle model for:

$$\begin{aligned} \varepsilon&= \varepsilon _{k} + q_s \varepsilon _{s} + (q_h+1) \varepsilon _{\ell } + \ell (q_s+q_h+1) q_s /2^{\beta } \\ t&\approx t' - O(q_s\cdot t_{{\mathsf {Sign}}}) \end{aligned}$$

where $t_{{\mathsf {Sign}}}$ denotes the average signing time. Furthermore, if $\mathsf {ID}$ is $\varepsilon _{c}$-unique, then $\mathsf {Sig}[\mathsf {ID}]$ is $(t,q_h,q_s,\varepsilon )$ strongly existentially unforgeable against adaptive chosen-message attacks in the random oracle model for:

$$\begin{aligned} \varepsilon&= \varepsilon _{k} + q_s (\varepsilon _{s}+\varepsilon _{c}) + (q_h+1) \varepsilon _{\ell } + \ell (q_s+q_h+1) q_s /2^{\beta } \\ t&\approx t' - O(q_s\cdot t_{{\mathsf {Sign}}}) \end{aligned}$$

Finally, the probability that $\mathsf {Sig}[\mathsf {ID}]$ outputs a valid signature is $1 - (1-\rho )^\ell$.

Remark 1

This is indeed a tight reduction, in the sense that the probability $\varepsilon$ of breaking the unforgeability of $\mathsf {Sig}[\mathsf {ID}]$ is tightly related to the probability $\varepsilon _k$ of breaking the underlying computational assumption. The other epsilon terms $\varepsilon _s,\varepsilon _\ell ,\varepsilon _c$ are statistical and hence unrelated to computational hardness.

3.2 Proof Overview

In order to prove the security of the signature scheme based on the security properties of the underlying lossy identification scheme, the main idea is to use honest transcripts generated by the identification scheme to answer signature queries made the adversary by appropriately programming the random oracle. More precisely, let $(cmt,ch,rsp)$ be a valid transcript (i.e., ${\mathsf {Verify}}(pk,cmt,ch,rsp)=1)$. To answer a query $m$ to the signing oracle, we need to program the random oracle to set $H(cmt,m)=ch$ so that $(cmt,rsp)$ is a valid signature for $m$. Unfortunately, this programming may conflict with previous values output by the hash oracle. To address this problem, the first step of the proof is to show that such collisions happen with probability at most $\ell (q_s+q_h+1) q_s /2^{\beta }$.

Next, we make a sequence of small changes to the security experiment to be able to bound the success probability of the forger. The first significant modification is to change the simulation of the signing oracle so that it no longer uses the secret key. This is done by replacing the transcript generation oracle $\mathsf {Tr}^{\mathsf {ID}}_{pk,sk,k}$ with its simulated version $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk,k}$. Since we make at most $q_s$ calls to $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk,k}$, the difference in the success probability of the forger changes by at most $q_s \varepsilon _{s}$ due to the simulatability of $\mathsf {ID}$.

The second important modification is to replace the key generation algorithm with its lossy version. Since the secret key is no longer needed in the simulation of the signing oracle, the difference in the success probability of the forger changes by at most $\varepsilon _{k}$ due to the key-indistinguishability of $\mathsf {ID}$.

The third significant modification, which only applies to the case of the proof of strong existential unforgeability, is to abort whenever the adversary outputs a valid forgery $(m,(cmt,rsp))$ for which $(cmt,rsp')$ was one of the values returned by the signing oracle on input $m$ and $rsp'\not =rsp$. Clearly, the difference in the success probability of the forger changes by at most $q_s \varepsilon _{c}$ due to the uniqueness of $\mathsf {ID}$.

Finally, we can bound the success probability of the forger in this final experiment by relating this probability with that of solving the impersonation problem with respect to lossy keys. Since we need to guess the hash query which will be used in the forgery to be able to break the underlying impersonation problem, we lose a factor $q_h+1$ in the reduction, resulting in the term $(q_h+1) \varepsilon _{\ell }$ in the theorem.

3.3 Proof Details

In order to prove Theorem 1, we will use a sequence $\mathbf {Exp}_0, \ldots , \mathbf {Exp}_6$ of hybrid experiments, where $\mathbf {Exp}_0$ is the actual experiment defining the strong existential unforgeability of the signature scheme and $\mathbf {Exp}_6$ is an experiment, in which we can easily bound the success probability of the forger. For $i=0,\ldots ,6$, we also define an event $\delta _i$ which corresponds to the probability that the adversary $\mathcal {F}$ successfully outputs a valid forgery in experiment $\mathbf {Exp}_i$.

For simplicity, we will assume in the remainder of the proof that the set of hash queries made by adversary against the strong existential unforgeability of the signature scheme always includes the pair $(cmt,m)$ involved in the forgery. This is without loss of generality since, given an adversary that does not ask such query to the hash oracle, we can always build another adversary with the same success probability and approximately the same running time, which will always ask such query. This will, however, increase the total number of hash queries by 1.

$\mathbf {Exp}_0$. In this experiment, the (hypothetical) challenger runs $(pk,sk) \overset{\$}{\leftarrow }{\mathsf {KeyGen}}(1^k)$, sets the hash $(hc)$ and sign counters $(sc)$ to $0$, initializes the list of hash queries and responses to empty, and returns $pk$ to the forger $\mathcal {F}$.

Whenever $\mathcal {F}$ asks a hash query $(cmt,m)$, the challenger checks if this query has already been asked and returns the same answer if this is the case. If this is a new query, then the challenger chooses a random string $ch$ from the challenge space and returns it to $\mathcal {F}$. It also increments $hc$ by 1 and adds $(cmt,m)$ and $ch$ to the list of hash queries and responses.

Whenever $\mathcal {F}$ asks for a sign query $m$, the challenger computes the signature $\sigma$ as in the signing algorithm (i.e., $\sigma \overset{\$}{\leftarrow }{\mathsf {Sign}}(sk,m))$, increments $sc$ by 1 and returns $\sigma =(cmt,rsp)$ to $\mathcal {F}$. In doing so, it checks whether $H(cmt,m)$ has already been defined. If it has not, then the challenger chooses a new value $ch$ from the challenge space, sets $H(cmt,m)=ch$ and computes $rsp$ using this value.

Finally, when $\mathcal {F}$ outputs a forgery $(m,\sigma )$, where $\sigma$ was not outputted by the signing oracle on input $m$, the challenger returns ${\mathsf {Verify}}(pk,m,\sigma )$ as the output of the experiment. By definition, we have ${\Pr \left[ \,{\delta _0}\,\right] } = \varepsilon$.

$\mathbf {Exp}_1$. Let $\mathsf {bad}$ be a boolean variable initially set to $\mathsf {false}$. In this experiment, the challenger changes the simulation of the signing oracle so that it sets $\mathsf {bad}$ to $\mathsf {true}$ whenever $H(cmt,m)$ has already been defined (i.e., $H(cmt,m)\not =\bot$). Moreover, when $\mathsf {bad}$ is set, the challenger chooses a random value $ch$ from the challenge space and uses it (instead of predefined value $H(cmt,m)$) to compute the response. If $\mathsf {bad}$ is not set, then the challenger proceeds with the simulation as in $\mathbf {Exp}_0$.

Let $\mathsf {Bad}$ define the event that a hash query causes the experiment to set $\mathsf {bad}$ to $\mathsf {true}$. Clearly, the difference in the success probability between $\mathbf {Exp}_0$ and $\mathbf {Exp}_1$ can be upper-bounded by ${\Pr \left[ \,{\mathsf {Bad}}\,\right] }$ since these experiments only differ after $\mathsf {bad}$ is set. To compute this probability, we can assume the worst-case, in which all $q_h+1$ hash queries are asked at the beginning of the experiment. In this worst-case scenario, the probability that the $i$-th signing query causes the experiment to set $\mathsf {bad}$ to $\mathsf {true}$ is $(\ell (i-1)+q_h+1)/2^{\beta }$, where the factor $\ell$ is due to the fact that signing oracle may attempt to generate a response up to $\ell$ times. By summing up over all $q_s$ signing queries, we have ${\Pr \left[ \,{\mathsf {Bad}}\,\right] } \le \ell (q_s+q_h+1) q_s /2^{\beta }$. As a result, we have

$$\begin{aligned} \big | {\Pr \left[ \,{\delta _1}\,\right] } - {\Pr \left[ \,{\delta _0}\,\right] } \big | \le \ell (q_s+q_h+1) q_s /2^{\beta }. \end{aligned}$$

$\mathbf {Exp}_2$. In this experiment, the challenger changes the simulation of the signing oracle so that it no longer sets the variable $\mathsf {bad}$. Since the latter does not change the output of the experiment, we have ${\Pr \left[ \,{\delta _2}\,\right] } = {\Pr \left[ \,{\delta _1}\,\right] }$.

$\mathbf {Exp}_3$. In this experiment, the challenger changes the simulation of the signing oracle so that the values $(cmt,ch,rsp)$ are computed using the transcript generation function $\mathsf {Tr}^{\mathsf {ID}}_{pk,sk,k}$ as a subroutine. Since the challenge values used to answer signing queries are chosen uniformly at random and independently of previous hash queries since $\mathbf {Exp}_1$, this change does not affect the output of the experiment. Hence, ${\Pr \left[ \,{\delta _3}\,\right] } = {\Pr \left[ \,{\delta _2}\,\right] }$.

$\mathbf {Exp}_4$. In this experiment, the challenger changes the simulation of the signing oracle so that the values $(cmt,ch,rsp)$ used to answer signing queries are computed right after the generation of the public and secret keys, still using the transcript generation function $\mathsf {Tr}^{\mathsf {ID}}_{pk,sk,k}$ as a subroutine. Since this change does not affect the output of the experiment, we have ${\Pr \left[ \,{\delta _4}\,\right] } = {\Pr \left[ \,{\delta _3}\,\right] }$.

$\mathbf {Exp}_5$. In this experiment, the challenger computes the values $(cmt,ch,rsp)$ used to answer signing queries using the simulated transcript generation function $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk,k}$ as a subroutine. Since we make at most $q_s$ calls to $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk,k}$ and since the statistical distance between the distributions output by $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk,k}$ and $\mathsf {Tr}^{\mathsf {ID}}_{pk,sk,k}$ is at most $\varepsilon _{s}$ due to the simulatability of $\mathsf {ID}$, we have

$$\begin{aligned} \big | {\Pr \left[ \,{\delta _5}\,\right] } - {\Pr \left[ \,{\delta _4}\,\right] } \big | \le q_s \varepsilon _{s}. \end{aligned}$$

We note that at this point, the secret key is no longer needed in the experiment and all hash queries are answered with random values in the challenge space. Moreover, all the values $(cmt,ch,rsp)$ used to answer signing queries are computed via the simulated transcript generation function $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk,k}$ at the beginning of the experiment (after the key generation step) and independently of the hash queries.

$\mathbf {Exp}_6$. In this experiment, the challenger generates $(pk,\bot )$ via ${\mathsf {LosKeyGen}}(1^k)$. Since the secret key is no longer needed in the experiment and the values $(cmt, ch, rsp)$ are computed using $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk,k}$ as a subroutine, it is easy to build an adversary $\mathcal B$ that $(t',\varepsilon ')$ solves the key-indistinguishability of $\mathsf {ID}$ if $|{\Pr \left[ \,{\delta _6}\,\right] } - {\Pr \left[ \,{\delta _5}\,\right] }| = \varepsilon '$, where $t'\approx t + O(q_s\cdot t_{{\mathsf {Sign}}})$. Since, $\mathsf {ID}$ is $(t',\varepsilon )$-key-indistinguishable by assumption, we have

$$\begin{aligned} \big | {\Pr \left[ \,{\delta _6}\,\right] } - {\Pr \left[ \,{\delta _5}\,\right] } \big | \le \varepsilon _{k}. \end{aligned}$$

$\mathbf {Exp}_{7}$. In this experiment, the challenger aborts whenever the adversary outputs a valid forgery $(m,(cmt,rsp))$ for which $(cmt,rsp')$ was one of the values returned by the signing oracle on input $m$ and $rsp'\not =rsp$. Since such forgeries are not considered valid under the existential unforgeability security notion, we have that ${\Pr \left[ \,{\delta _7}\,\right] } = {\Pr \left[ \,{\delta _6}\,\right] }$ in the case of the proof of existential unforgeability. Moreover, in the case of the proof of strong existential unforgeability, the difference in the success probability of the forger changes by at most $q_s \varepsilon _{c}$ due to the uniqueness of $\mathsf {ID}$. Hence, $\big | {\Pr \left[ \,{\delta _7}\,\right] } - {\Pr \left[ \,{\delta _6}\,\right] } \big | \le q_s \varepsilon _{c}$ in the latter case.

We now claim that ${\Pr \left[ \,{\delta _7}\,\right] } \le (q_h + 1) \varepsilon _{\ell }$. To prove this, it suffices to show that we can use the forger $\mathcal {F}$ in $\mathbf {Exp}_7$ to build an adversary $\fancyscript{I}$ that $\varepsilon$ solves the impersonation problem with respect to lossy keys. Let $pk$ be the lossy key that $\fancyscript{I}$ receives as input in $\mathbf {Exp}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k)$. Next, $\fancyscript{I}$ chooses a random index $i$ in $\{1,\ldots ,q_h+1\}$ and runs $\mathcal {F}$ on input $pk$. As in $\mathbf {Exp}_7, \fancyscript{I}$ computes the values $(cmt, ch, rsp)$ using its transcript generation oracle $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk,k}$. Whenever $\mathcal {F}$ asks a $j$-th hash query $(cmt_j,m_j), \fancyscript{I}$ first checks if $i=j$. If this is not the case, then $\fancyscript{I}$ chooses a value $ch$ uniformly at random from the challenge space and returns it to $\mathcal {F}$ as in $\mathbf {Exp}_7$. However, if $i=j$, then $\fancyscript{I}$ saves its internal state in $st$ and returns $cmt_i$ to its challenger in $\mathbf {Exp}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k)$. Let $(st,ch^*)$ be the input that $\fancyscript{I}$ gets back from the challenger. $\fancyscript{I}$ then sets $H(cmt_i,m_i)=ch^*$ and returns it to $\mathcal {F}$. It then continues the simulation exactly as in $\mathbf {Exp}_7$. Eventually, $\mathcal {F}$ outputs a forgery $(m^*, (cmt^*,rsp^*)). \fancyscript{I}$ then returns $rsp^*$ as its output in $\mathbf {Exp}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k)$.

Clearly, $\fancyscript{I}$ simulates $\mathcal {F}$’s environment exactly as in $\mathbf {Exp}_7$. Moreover, if $(cmt^*,m^*)=(cmt_i,m_i)$, then the probability that $\mathbf {Exp}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k)$ outputs $1$ is exactly the probability that $\mathbf {Exp}_7$ outputs $1$. Since this happens with probability $1/(q_h+1)$ and since $\mathsf {ID}$ is $\varepsilon _{\ell }$-lossy, it follows that

$$\begin{aligned} {\Pr \left[ \,{\delta _7}\,\right] } \le (q_h + 1) \varepsilon _{\ell }. \end{aligned}$$

To conclude the proof, we point out that, since $\mathsf {ID}$ is $\rho$ complete, the signing algorithm may fail to produce a valid signature with probability $(1-\rho )^\ell$.$\square$

4 A Signature Scheme Based on the DSDL Problem

In this section, we describe our short discrete log-based signature scheme. While it looks similar to the prime-order version of the Girault–Poupard–Stern identification scheme [20, 26, 49], the proof strategy is in fact closer to the one used by Katz and Wang for their DDH-based signature scheme [22, 32]. We first present a lossy identification scheme and then use the generic transformation from the previous section to obtain the signature scheme.

4.1 Description of the Lossy Identification Scheme

The full description of our lossy identification scheme based on the DSDL problem is provided in Fig. 2. The public parameters of the identification scheme are a cyclic group ${\mathbb {G}}$ of prime order $q$ (typically chosen as the subgroup of order $q$ in $\mathbb {Z}_p^*$ where $p$ is prime²), a generator $g$ of ${\mathbb {G}}$, and size parameters $c,k,k'$. The secret key is a small (relative to $q$) integer $x$, and the public key consists of a single group element $h = g^x\mod p$. The prover’s first move is to generate a small (but larger than $x$) random integer $y$ and send $u = g^y$ as a commitment to the verifier. Next, the (honest) verifier picks a value $e$ uniformly in $\{0,\ldots ,2^k-1\}$ and sends it to the prover. After receiving $e$ from the verifier, the prover computes $z=ex+y$ (without any modular reduction) and checks whether $z$ is in the range $\{2^{k+c},\dots ,2^{k+k'+c}-1\}$. If $z$ is in the “correct” range, then the prover sends $z$ to the verifier, who can check the verifying equation $u = g^z/h^e$ to authenticate the prover. If $z$ is outside the correct range, the prover sends $\bot$ to indicate failure—as in [37, 38], this check is important to ensure that the distribution of the value $z$ is independent of the secret key $x$; it is worth noting that the original GPS scheme did not require such checks, but required a larger “masking parameter” $y$.

Fig. 2

A lossy identification scheme based on DSDL

4.2 Security of the Identification Scheme

As noted above, the scheme in Fig. 2 is a secure lossy ID scheme. More precisely, we establish the following theorem.

Theorem 2

If ${\mathbb {G}}$ is a $(t,\varepsilon )-c$-DSDL group, then the identification scheme in Fig. 2 is perfectly simulatable, $\rho$-complete, $(t,\varepsilon )$-key-indistinguishable and $\varepsilon _{\ell }$-lossy for:

$$\begin{aligned} \rho&= 1-2^{-k'} \\ \varepsilon _{\ell }&\le 2^{2k+k'+c+2}/q + 1/2^k. \end{aligned}$$

It is also perfectly unique with respect to lossy keys.

We first establish the following lemma.

Lemma 1

Let all the variables and their distributions be as in Fig. 2. Then, the probability that $z = ex+y$ computed by the prover belongs to the correct interval $\{2^{k+c},\dots ,2^{k+k'+c}-1\}$ is $1-2^{-k'}$. In particular, the expected number of iterations required to identify the prover is $1/(1-2^{-k'})$. Moreover, the value $z$ in the transcript is uniformly distributed in $\{2^{k+c},\dots ,2^{k+k'+c}-1\}$.

Proof

Since the distribution of $e$ is independent of that of $y$, the value $z = ex+y$ is uniformly distributed in the set $\{ex,ex+1, \dots , ex+2^{k+k'+c}-1\}$, which is of cardinality $2^{k+k'+c}$ and properly contains $G = \{2^{k+c},\dots ,2^{k+k'+c}-1\}$. Therefore, the probability that $z$ belongs to $G$ is exactly $|G|/2^{k+k'+c} = 1-2^{-k'}$ as required. The expected number of iterations in the identification scheme follows immediately.

Furthermore, for any element $z_0\in G$, we have:

$$\begin{aligned} \Pr [ z=z_0 | z\in G] = \frac{\Pr [ z=z_0 ]}{\Pr [ z\in G ]} = \frac{1/2^{k+k'+c}}{|G|/2^{k+k'+c}} = \frac{1}{|G|} \end{aligned}$$

and thus provided that $z$ passes the test in the verification step, and we know that it is uniformly distributed in $G$, hence the final claim. $\square$

With these lemmas, we are ready to establish the stated properties from Figs. 6 and 7, namely completeness, simulatability of the transcripts, indistinguishability of the keys, lossiness and uniqueness.

Completeness. If the public and secret keys are generated with the “normal” key generation algorithm, then the interaction with an honest verifier should result in acceptance with significant probability. Lemma 1 shows that this probability is exactly $1-2^{-k'}$.

Simulatability of the transcripts. Let $\mathsf {Tr}^{\mathsf {ID}}_{pk,sk}$ be the honest transcript generation function corresponding to a key pair $(pk,sk)$ generated by the “normal” key generation algorithm. Recall from Sect. 3 that it outputs the full transcript $(cmt, ch, rsp)$ if $rsp\ne \bot$ and $(\bot , \bot , \bot )$ otherwise. Then, there should exist an efficient transcript generation simulator $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk}$ depending only on $pk$ (not on $sk$) producing transcripts whose distribution is statistically close to that of $\mathsf {Tr}^{\mathsf {ID}}_{pk,sk}$. We construct $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk}$ as follows. The public key $pk$ consists of a single group element $h = g^x\in {\mathbb {G}}$. To generate a “simulated” transcript, $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk}$ picks $z$ uniformly at random in the range $\{2^{k+c},\ldots , 2^{k+k'+c}-1\}$ and chooses $e$ uniformly at random in the range $\{0, \ldots ,2^k-1\}$. Then, it computes $u$ as $g^z/h^e$. Finally, it returns $(u,e,z)$ with probability $1-2^{-k'}$ and $(\bot , \bot , \bot )$ otherwise.

Then, according to Lemma 1, if $pk= h$ is a correct public key (of the form $g^x$ with $0\le x\le 2^c-1$), the output distribution of $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk}$ is exactly the same as that of $\mathsf {Tr}^{\mathsf {ID}}_{pk,sk}$.

Indistinguishability of keys. The public key generated by a “lossy” key generation algorithm should be indistinguishable from that generated by the “normal” key generation algorithm. The indistinguishability of the lossy and normal key is exactly decisional assumption that it is difficult to distinguish short discrete logs.

Lossiness. Given a lossy public key $h$ (which is thus of the form $g^x$ for $x$ uniformly random in $\mathbb {Z}_q$), we have to show that the probability that an impersonator interacting with an honest verifier generates a valid response is negligible.

Let $\fancyscript{I}$ be an impersonator for the $\mathbf {Exp}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k)$ experiment described in Fig. 6. We first claim that, with high probability over the choice of $x$, for any choice of $u\in {\mathbb {G}}$, there is at most one value $e$ such that $u$ can be written as $g^z\cdot h^{-e}$ for some $z$ in the appropriate interval. Indeed, if two pairs $(z,e)\ne (z',e')$ exist, we have $g^z\cdot h^{-e} = g^{z'}\cdot h^{-e'}$, i.e., $z-xe \equiv z'-xe' \pmod q$. This implies that:

$$\begin{aligned} x \equiv \frac{z-z'}{e-e'} \pmod q \end{aligned}$$

which means that $x$ can be written as a modular ratio between an element of $\{-2^{k+k'+c}+1,\dots ,2^{k+k'+c}-1\}$ and an element of $\{-2^k+1,\dots ,2^k-1\}$. But there are at most $2^{2k+k'+c+2}$ such ratios. Thus, two pairs can only exist with probability at most $2^{2k+k'+c+2}/q$.

Assume that $x$ does not satisfy that relation. Then, for any possible commitment, the impersonator $\fancyscript{I}$ makes, there is at most one value of the uniformly random challenge $e\in \{0,\dots ,2^k-1\}$ for which a valid response can be constructed. Thus, the success probability of $\fancyscript{I}$ is not higher than $1/2^k$.

As a result, we obtain the required bound on the advantage of $\fancyscript{I}$ in the experiment $\mathbf {Exp}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k)$:

$$\begin{aligned} \big | \mathbf {Adv}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k) \big | =\big | {\Pr \left[ \,{\mathbf {Exp}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k)=1}\,\right] }\big | \le 2^{2k+k'+c+2}/q + 1/2^k. \end{aligned}$$

Uniqueness. Finally, all it remains to establish is that, given $pk$ a public key output by ${\mathsf {LosKeyGen}}(1^k)$ and $(u,e,z)$ a valid transcript output by the transcript generation function $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk,k}()$, there never exists a new response $z'\ne z$ for which ${\mathsf {Verify}}(pk,u,e,z') = 1$. But this is clear: The verification equation implies $g^{z'}/h^e = u = g^{z}/h^e$, hence $g^{z'} = g^z$, and thus $z'=z$, a contradiction. $\square$

4.3 Conversion to a Signature Scheme

In order to obtain our signature scheme based on the DSDL problem, we apply the transform provided in the previous section to the identification scheme in Fig. 2. The full description of the resulting scheme is provided in Fig. 3. In addition to those of the underlying identification scheme, the public parameters of the signature scheme also include the maximum number of signing attempts $\ell$ and a random oracle $H:\{0,1\}^*\rightarrow \{0,\dots ,2^k-1\}$. The key pair is as before. To sign a message $m$, we generate a small (but larger than $x$) random integer $y$ and compute $e \leftarrow H(g^y\mod p,m)$. Finally, we set $z=ex+y$ and check whether $z$ is in the correct range. If it is not, we restart the signature process. In case of $\ell$ failures, the signing algorithm simply outputs $(\bot ,\bot )$ to indicate failure. Otherwise, the signature will consist of the pair $\sigma =(z,e)$. Since the probability that $z$ is not in the correct range is smaller than $1/2^{k'}$, the signing algorithm will fail with probability at most $(1-1/2^{k'})^{\ell }$. Moreover, the average number of iterations is $1/(1- 1/2^{k'})$.

Fig. 3

DSDL-based signature scheme

As a direct consequence of Theorems 1 and 2, we get:

Theorem 3

If ${\mathbb {G}}$ is a $(t',\varepsilon ')-c$-DSDL group, then this signature scheme is $(t,q_h,q_s,\varepsilon )$ strongly existentially unforgeable against adaptive chosen-message attacks in the random oracle model for:

$$\begin{aligned} \varepsilon&= \varepsilon ' + (q_h+1)\cdot \frac{2^{2k+k'+c+2}}{q} + \ell (q_s+q_h+1) \cdot \frac{q_s}{2^k} \\ t&\approx t' - O(q_s\cdot t_1) \end{aligned}$$

(where $t_1$ is the cost of an exponentiation in ${\mathbb {G}}$), and it outputs a valid signature with probability $1 - 2^{k'\ell }$.

Remarks

• 1. The scheme in Fig. 3 uses $(z,e)$ instead of $(z,g^y)$ as the signature since $(z,e)$ can be used to recover $g^y$, but the length of $e$ is shorter than that of $g^y$.

• 2. This is an online/offline signature scheme: It can be used with coupons by precomputing $(y,g^y\mod p)$ independently of the message. In the rare case when $z$ is not in the right interval (which can be checked without even computing a multiplication), it suffices to use another coupon.

• 3. As in [22], it is possible to eliminate the terms depending on $q_s$ in $\varepsilon$, making the security reduction even tighter, by ensuring that the masking parameter $y$ is always the same for a given message. This can be done either by making the scheme stateful (keeping track of the randomness on signed messages) or by generating $y$ as a deterministic, pseudorandom function of the signed message and the private key, as seen in Fig. 4 (but the resulting scheme is no longer online/offline).

Fig. 4

Fully tight DSDL-based signature scheme

4.4 Suggested Parameters

In Table 1, we propose parameters for an instantiation of our scheme at the $80$-bit security level. The size of the public key $g^x\mod p$ is $1024$ bits, and the size of the signature $(z,e)$ is $k+k'+c+k=328$ bits. With those parameters, there is a $1/2^{k'}=1/256$ chance that the signing algorithm will have to be repeated (or another coupon will have to be used), but this has little effect on the expected running time. If a lower probability of rejection is preferred, it is possible to increase $k'$ to $16$ or $24$, for a relatively insignificant increase in signature size and online signature cost.

Table 1 Example parameters for the DSDL scheme

A detailed efficiency comparison of our scheme with other existing signature schemes in $\mathbb {Z}_p^*$ with tight reductions in the random oracle model (Goh–Jarecki [21], Chevallier-Mames [9] and Katz–Wang [32]) is provided in Table 2. In particular, a full signature computation requires a single exponentiation of $248$ bits in $\mathbb {Z}_p^*$ with fixed base, which is at least as efficient as comparable schemes, and when used with coupons, the scheme is possibly the fastest option available, with an online cost of one single integer multiplication between a $80$-bit number and a $160$-bit number, and no modular reduction.

Table 2 Efficiency comparison between known signature schemes with tight reductions in the random oracle model, when instantiated over $\mathbb {Z}_p^*$ for $p$ a $1024$-bit prime ($80$-bit security level)

5 A Signature Scheme Based on Lattices

In this section, we present a signature scheme whose security is based on the hardness of the $\text{ Ring-LWE }$ problem. Toward this goal, we first describe a lossy identification scheme based on the $\text{ Ring-LWE }$ problem and then use our generic transformation in Sect. 3 to obtain the signature scheme.

5.1 Description of the Lossy Identification Scheme

The full description of our lossy identification scheme based on lattices is described in Fig. 5, and for convenience, we list the notation used in the scheme in Table 3. The secret key consists of two polynomials $\mathbf{s}_1,\mathbf{s}_2$ with “small” coefficients chosen from the distribution $D_{\mathcal {R},\sigma }$ (as defined in Sect. 2.2), and the public key consists of a randomly chosen element $\mathbf{a}\in \mathcal {R}^\times$ and of the value $\mathbf{t}=\mathbf{a}\mathbf{s}_1+\mathbf{s}_2$. Under the $\text{ Ring-LWE }$ assumption in the ring $\mathcal {R}$, the public key is thus indistinguishable from a uniformly random element in $\mathcal {R}^\times \times \mathcal {R}$.

Fig. 5

A lossy identification scheme based on lattices

Table 3 Parameters for the lattice-based scheme

In our protocol, the prover’s first move is to create two “small” polynomials $\mathbf{y}_1,\mathbf{y}_2$ (larger than $\mathbf{s}_1,\mathbf{s}_2$ by a factor $\approx n$) from the set $\mathcal {M}$ and then send the value $\mathbf{u}= \mathbf{a}\mathbf{y}_1+\mathbf{y}_2$ to the verifier. Upon receipt of $\mathbf{u}$, the (honest) verifier chooses a value $\mathbf{c}$ uniformly at random in the set $\mathcal {C}$ and sends it to the prover. After receiving $\mathbf{c}$ from the verifier, the prover sets $\mathbf{z}_1\leftarrow \mathbf{s}_1\mathbf{c}+\mathbf{y}_1$ and $\mathbf{z}_2\leftarrow \mathbf{s}_2\mathbf{c}+\mathbf{y}_2$ and checks whether the $\mathbf{z}_i$s are both in $\mathcal {G}$. If they are, the prover then sends the response $(\mathbf{z}_1,\mathbf{z}_2)$ to the verifier. If one (or both) of the $\mathbf{z}_i$ is outside of $\mathcal {G}$ (which happens with probability approximately $1-1/e^2$), then the prover simply sends $(\bot ,\bot )$. Finally, the verifier simply checks whether the $\mathbf{z}_i$s are in $\mathcal {G}$ and that $\mathbf{a}\mathbf{z}_1+\mathbf{z}_2=\mathbf{t}\mathbf{c}+\mathbf{u}$.

At this point, we should mention that using the recent techniques from [39], it is possible to lower the bitsize of the response $(\mathbf{z}_1,\mathbf{z}_2)$ by choosing the polynomials $\mathbf{y}_1,\mathbf{y}_2$ from a normal distribution and then doing a somewhat more involved rejection sampling when deciding whether to send $(\mathbf{z}_1,\mathbf{z}_2)$ or $(\bot ,\bot )$ to the verifier.

The idea of checking whether the polynomials $\mathbf{z}_i$ are in some set and redoing the signature otherwise is the aborting technique first used in [37, 38] and is crucial in Fiat-Shamir type lattice schemes for masking the secret keys $\mathbf{s}_i$ while keeping the response size small and the security reduction meaningful. Intuitively, the larger the length of the elements $\mathbf{z}_i$ with respect to the secret keys $\mathbf{s}_i$, the easier it is for adversaries to break the identification scheme, and so we would be required to set the parameters higher to avoid attacks.

5.2 Security of the Identification Scheme

The idea for the security proof is as follows: We first show in Lemma 3 and Corollary 1 that for any $\mathbf{s}_1,\mathbf{s}_2$, the distribution of $(\mathbf{z}_1,\mathbf{z}_2)$ is statistically close to uniform in the set $\mathcal {G}$. This fact allows us to simulate the transcript generation algorithm without knowing the secret key by picking $\mathbf{z}_1,\mathbf{z}_2$ randomly from $\mathcal {G}$, picking $\mathbf{c}$ randomly from $\mathcal {C}$ and computing the corresponding challenge as $\mathbf{u}= \mathbf{a}\mathbf{z}_1+\mathbf{z}_2-\mathbf{t}\mathbf{c}$. On the other hand, the hardness of the $\text{ Ring-LWE }$ problem says that a normal public key $(\mathbf{a},\mathbf{a}\mathbf{s}_1+\mathbf{s}_2)$ is indistinguishable from a “lossy” key $(\mathbf{a},\mathbf{t})$ chosen uniformly at random in $\mathcal {R}^\times \times \mathcal {R}$. This is enough to see that we have constructed a lossy ID scheme if we can prove that such a random key $(\mathbf{a},\mathbf{t})$ is indeed lossy.

To do so, we apply a similar strategy as for the short discrete log-based scheme from Sect. 4 by showing that in the lossy case, for a given commitment $\mathbf{u}$, the existence of two valid challenge–response pairs $(\mathbf{c},\mathbf{z})$ and $(\mathbf{c}',\mathbf{z}')$ implies that $\mathbf{t}$ is in some sense a “short modular ratio,” a property that is only satisfied with negligible probability. However, a technical issue that did not occur in Sect. 4 is that the probability that $\mathbf{c}{-}\mathbf{c}'$ is not invertible in $\mathcal {R}$ is non-negligible. We circumvent this problem by showing that, with high probability, it becomes invertible in a quotient of $\mathcal {R}$ that is not too small. This is reminiscent of techniques used, for example, in [40, Theorem 4.2].

We obtain security for parameters such that the ratio between $p$ and $\sigma$ is $\hbox {poly}(n)$, and for such parameters the Ring-LWE problem is believed to be exponentially hard, as evidenced by the quantum reduction of [36, Theorem 3.6].

Theorem 4

If $p \gg \sigma ^{2/\alpha }\cdot n^{3/\alpha +\eta }$ for some $\eta >0$, and the Ring-LWE problem over $\mathcal {R}$ with standard deviation $\sigma$ is $(\varepsilon ,t)$-hard, then the identification scheme in Fig. 5 is $\varepsilon _s$-simulatable, $\rho$-complete, $(t,\varepsilon )$-key-indistinguishable and $\varepsilon _{\ell }$-lossy, for:

If, moreover, $p\gg \sigma ^{2/\alpha }\cdot n^{4/\alpha +\eta }$ for some $\eta >0$, then the identification scheme is also $\varepsilon _c$-unique for some $\varepsilon _c\le \hbox {negl}(n)$.

Proof

Fix an element $\mathbf{a}\in \mathcal {R}$ and a rational number $\alpha \in (0,1)$ whose denominator is a small power of $2$, so that $d = \alpha n$ is an integer (this constant $\alpha$ will ultimately be chosen arbitrarily close to $1$). Define an element $\mathbf{t}\in \mathcal {R}$ to be an $\alpha$-partial modular ratio (with respect to $\mathbf{a}$) when there exists $(\mathbf{z}_1,\mathbf{z}_1',\mathbf{z}_2,\mathbf{z}_2')\in \mathcal {G}^4, (\mathbf{c},\mathbf{c}')\in \mathcal {C}^2$ and a polynomial $Q\in \mathbb {Z}_p[\mathbf{x}]$ of degree $d$ dividing $\mathbf{x}^n+1$ such that:

$$\begin{aligned} \mathbf{c}{-}\mathbf{c}' \text { is invertible mod } Q\quad \text {and}\quad \mathbf{t}\equiv \frac{\mathbf{a}(\mathbf{z}_1-\mathbf{z}_1') + (\mathbf{z}_2-\mathbf{z}_2')}{\mathbf{c}{-}\mathbf{c}'} \pmod Q. \end{aligned}$$

(1)

We will need some technical lemmas, proved in Appendix 1. $\square$

Lemma 2

Let $\mathbf{t}$ be a uniformly random element of $\mathcal {R}$. Then:

$$\begin{aligned} \Pr [ \mathbf{t}\text { is an }\alpha -\text {partial modular ratio} ] \le \left( {\begin{array}{c}n\\ d\end{array}}\right) \left( \frac{33n^3\sigma ^2\log ^7{n}}{p^\alpha }\right) ^n \end{aligned}$$

In particular, if $p\gg \sigma ^{2/\alpha }\cdot n^{3/\alpha +\eta }$ for some $\eta >0$, then this probability is negligible.

Lemma 3

If $\mathbf{s}\overset{\$}{\leftarrow }D_{\mathcal {R},\sigma }, \mathbf{c}\overset{\$}{\leftarrow }\mathcal {C}$, and $\mathbf{y}\overset{\$}{\leftarrow }\mathcal {M}$, then the following inequalities hold:

$$\begin{aligned}&\Pr [\mathbf{s}\mathbf{c}+\mathbf{y}\in \mathcal {G}] \ge \frac{1}{e}-\frac{1}{en}-e^{-\varOmega (\log ^2{n})}, \\ \sum _{\mathbf{g}\in \mathcal {G}}&\left| \Pr [\mathbf{s}\mathbf{c}+\mathbf{y}= \mathbf{g}\ |\ \mathbf{s}\mathbf{c}+\mathbf{y}\in \mathcal {G}] - \frac{1}{|\mathcal {G}|} \right| \le e^{-\varOmega (\log ^2{n})}. \end{aligned}$$

The following corollary is an immediate consequence of Lemma 3.

Corollary 1

The probability that the $\mathbf{z}_1$ and $\mathbf{z}_2$ computed by the prover upon receipt of the challenge $\mathbf{c}$ are both in $\mathcal {G}$ is at least $\frac{1}{e^2}-\frac{2}{en}$. Moreover, the distributions of $\mathbf{z}_1$ and $\mathbf{z}_2$ when this is satisfied are statistically close to uniform in $\mathcal {G}$.

Turning to the proof, we follow the same steps as in Sect. 4. Following Fig. 6, we prove the completeness property of the identification scheme, the simulatability of the transcripts, the indistinguishability of the keys and the lossiness property.

Completeness. Corollary 1 shows that, given a key pair generated by the normal key generation algorithm, the prover interacting with a honest verifier produces a valid response with probability at least $1/e$, which is non-negligible as required.

Simultability of the transcripts. Given a normal public key $pk= (\mathbf{a},\mathbf{t})$, we can construct a simulator $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk}$ of the real transcript generation oracle $\mathsf {Tr}^{\mathsf {ID}}_{pk,sk}$ as follows.

Let $\rho >1/e^2-2/(en)$ be the probability that the prover actually responds to an honest challenge instead of sending $\bot$ ($\rho$ is a constant depending only on the public parameters). We define $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk}$ to first pick a uniformly random triple $(\mathbf{z}_1,\mathbf{z}_2,\mathbf{c})\in \mathcal {G}\times \mathcal {G}\times \mathcal {C}$, then compute $\mathbf{u}= \mathbf{a}\mathbf{z}_1+\mathbf{z}_2-\mathbf{t}\mathbf{c}$ and finally output the transcript $(\mathbf{u},\mathbf{c},(\mathbf{z}_1,\mathbf{z}_2))$ with probability $\rho$ and $(\bot ,\bot ,\bot )$ otherwise.

By Corollary 1, the output distribution of $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk}$ is $\varepsilon$-statistically close to that of $\mathsf {Tr}^{\mathsf {ID}}_{pk,sk}$, with $\varepsilon \le e^{-\varOmega (\log ^2{n})}$.

Indistinguishability of keys. The public key generated by a lossy key generation algorithm should be computationally indistinguishable from that generated by the normal key generation algorithm. That is exactly the hardness of the $\text{ Ring-LWE }$ problem.

Lossiness. Let $\fancyscript{I}$ be an impersonator for the $\mathbf {Exp}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k)$ experiment described in Definition 6.

In the experiment, $\fancyscript{I}$ receives a lossy public key $(\mathbf{a},\mathbf{t})$, i.e., a pair of uniformly random elements in $\mathcal {R}$. In particular, by Lemma 2, the probability that $\mathbf{t}$ is an $\alpha$-partial modular ratio is bounded by a negligible value $\varpi _r$.

Assume that $\mathbf{t}$ is not an $\alpha$-partial modular ratio. We can see that for any choice of $\mathbf{u}\in \mathcal {R}$, only a negligible fraction of all elements $\mathbf{c}\in \mathcal {C}$ can satisfy a relation of the form $\mathbf{u}= \mathbf{a}\mathbf{z}_1+\mathbf{z}_2-\mathbf{t}\mathbf{c}$. Indeed, let $\mathbf{c}$ satisfy such a relation. Then, for any other $\mathbf{c}'$ satisfying a similar relation $\mathbf{u}= \mathbf{a}\mathbf{z}_1'+\mathbf{z}_2'-\mathbf{t}\mathbf{c}'$, we can write:

$$\begin{aligned} \mathbf{t}\cdot (\mathbf{c}-\mathbf{c}') = \mathbf{a}(\mathbf{z}_1-\mathbf{z}_1') + (\mathbf{z}_2-\mathbf{z}_2'). \end{aligned}$$

If there existed a factor $Q$ of $\mathbf{x}^n+1$ of degree $d = \alpha n$ such that $\mathbf{c}{-}\mathbf{c}'$ is invertible mod $Q$, then, reducing modulo $Q$, it would follow that $\mathbf{t}$ is an $\alpha$-partial modular ration: a contradiction. Therefore, we know that $\mathbf{c}-\mathbf{c}'$ is not invertible mod any degree-$d$ divisor of $\mathbf{x}^n+1$; this means that, under the $\mathbb {Z}_p$-algebra isomorphism $\mathcal {R}\rightarrow \mathbb {Z}_p^n$ sending a polynomial in $\mathcal {R}$ to its evaluations at all the roots of $\mathbf{x}^n+1$ (recall that $p\equiv 1\mod 2n$, so the cyclotomic polynomial splits completely), it maps to a vector with fewer than $d$ nonzero coefficients, or equivalently, more than $n-d$ zero coefficients. In particular, there exists a degree-$(n-d)$ divisor $\tilde{Q}$ of $\mathbf{x}^n+1$ such that $\mathbf{c}'\equiv \mathbf{c}\pmod {\tilde{Q}}$.

Now observe that the probability that a uniformly random element $\mathbf{c}'\in \mathcal {C}$ satisfies $\mathbf{c}'\equiv \mathbf{c}\pmod {\tilde{Q}}$ is at most $1/(2\log {n}+1)^{n-d}$. This is due to the fact that for any fixed value of the $d$ higher-order coefficients of $\mathbf{c}'$, the function $\mathbf{c}'\mapsto \mathbf{c}'\mod \tilde{Q}$ is a bijection between sets of size $(2\log {n}+1)^{n-d}$, as noted in [40, proof of Th. 4.2].

Thus, since there are $\left( {\begin{array}{c}n\\ n-d\end{array}}\right)$ factors of $\mathbf{x}^n+1$ of degree $n-d$, the total fraction of elements $\mathbf{c}'\in \mathcal {C}$ which can satisfy a relation of the form $\mathbf{u}= \mathbf{a}\mathbf{z}_1'+\mathbf{z}_2'-\mathbf{t}\mathbf{c}'$ is bounded by:

$$\begin{aligned} \varpi _c = \left( {\begin{array}{c}n\\ n-d\end{array}}\right) \left( \frac{1}{2\log {n}}\right) ^{n-d} \ll \left( \frac{1}{2\alpha ^\alpha (1-\alpha )^{1-\alpha }\log ^{1-\alpha }n}\right) ^n \end{aligned}$$

which is negligible as stated. And clearly, under the condition that $\mathbf{t}$ is not an $\alpha$-partial modular ratio, the impersonator cannot succeed with probability better than $\varpi _c$.

Overall, it follows that the advantage of $\fancyscript{I}$ in the experiment $\mathbf {Exp}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k)$ is bounded as:

$$\begin{aligned} \big | \mathbf {Adv}_{{\mathsf {ID},\fancyscript{I}}}^\mathrm {los\hbox {-}imp\hbox {-}pa}(k) \big | \le \varpi _r+\varpi _c = \hbox {negl}(n) \end{aligned}$$

as required.

Uniqueness. Finally, we assume that $p\gg \sigma ^{2/\alpha }\cdot n^{4/\alpha +\eta }$, and we want to show that, for a random choice of lossy key $pk\overset{\$}{\leftarrow }(\mathbf{a},\mathbf{t})\in \mathcal {R}^\times \times \mathcal {R}$ and a random output $(\mathbf{u},\mathbf{c},(\mathbf{z}_1,\mathbf{z}_2))$ of the transcript simulation algorithm $\mathsf {\widetilde{Tr}}^{\mathsf {ID}}_{pk}$ associated with $pk$, the probability that there exists another response $(\mathbf{z}_1',\mathbf{z}_2')\ne (\mathbf{z}_1,\mathbf{z}_2)$ such that the new transcript $(\mathbf{u},\mathbf{c},(\mathbf{z}_1',\mathbf{z}_2'))$ also verifies correctly is negligible.

To see this, note that the new transcript verifies correctly if and only if $\mathbf{a}\mathbf{z}_1' + \mathbf{z}_2' - \mathbf{t}\mathbf{c}= \mathbf{u}= \mathbf{a}\mathbf{z}_1 + \mathbf{z}_2 - \mathbf{t}\mathbf{c}$, or equivalently, if and only if:

$$\begin{aligned} \mathbf{a}(\mathbf{z}_1-\mathbf{z}_1') + (\mathbf{z}_2-\mathbf{z}_2') = 0. \end{aligned}$$

This means that $(\mathbf{z}_1-\mathbf{z}_1', \mathbf{z}_2-\mathbf{z}_2')$ is a nonzero vector in the lattice:

$$\begin{aligned} L_\mathbf{a}= \{ (\mathbf{w}_1,\mathbf{w}_2)\in \mathbb {Z}[\mathbf{x}]/(\mathbf{x}^n+1)\ :\ \mathbf{a}\mathbf{w}_1+\mathbf{w}_2 = 0 \pmod p \}. \end{aligned}$$

Now, according to [54, Lemma 3.3], for a uniformly random choice of $\mathbf{a}\in \mathcal {R}^\times$ and any $\nu >0$, the first minimum of $L_\mathbf{a}$ in the $\Vert \cdot \Vert _\infty$ norm satisfies:³

$$\begin{aligned} \lambda ^\infty _1(L_\mathbf{a}) \ge \frac{1}{\sqrt{n}} p^{1/2-\nu } \end{aligned}$$

except with probability $\le 2^{4n}p^{-2\nu n}$. In particular, if we set $\nu =(1-\alpha )/2$, we see that:

$$\begin{aligned} \lambda ^\infty _1(L_\mathbf{a}) \ge \sqrt{\frac{p^\alpha }{n}} \gg \sigma \cdot n^{3/2+\alpha \eta /2} \end{aligned}$$

except with probability at most $(4/p^{1-\alpha })^{2n}$.

On the other hand, we have seen that $(\mathbf{z}_1-\mathbf{z}_1', \mathbf{z}_2-\mathbf{z}_2')$ was a nonzero vector in $L_\mathbf{a}$, and its infinity norm is less than $2\sigma \cdot n^{3/2}\log ^3 n \ll \sigma \cdot n^{3/2+\alpha \eta /2}$. Therefore, the probability $\varepsilon _c$ that a new transcript that verifies correctly exists satisfies:

$$\begin{aligned} \varepsilon _c \le \left( \frac{4}{p^{1-\alpha }}\right) ^{2n} = \hbox {negl}(n). \end{aligned}$$

This concludes the proof. $\square$

5.3 Conversion to a Signature Scheme

In order to obtain our signature scheme based on lattices, we apply our generic transform to the identification scheme in Fig. 5. The full description of the resulting scheme is provided in Fig. 6. In addition to the public parameters of the underlying identification scheme, the parameters of the signature scheme also include the maximum number of signing attempts $\ell$ and a hash function $H:\{0,1\}^*\rightarrow \mathcal {C}$ mapping to polynomials in the set $\mathcal {C}$ and modeled as a random oracle. The secret key and public keys are as in the underlying identification scheme.

Fig. 6

Lattice-based signature scheme

The running time of the scheme is determined by the cost of the operations and also by the number of repetitions of the signing algorithm until it outputs a signature. Notice that the most expensive operations are the three multiplications of elements in the ring $\mathcal {R}$. Since multiplication in this ring can be performed using FFT in time $\tilde{O}(n\log {p})$, and $p=\hbox {poly}(n)$, each signature attempt takes time $\tilde{O}(n)$. We prove that the signature succeeds with probability approximately $1/e$ on each attempt (see Lemma 3 and Corollary 1) and so the running time of the signature (and verification) algorithms is $\tilde{O}(n)$.

The following result is a direct consequence of Theorems 1 and 4.

Theorem 5

If $p \gg \sigma ^{2/\alpha }\cdot n^{3/\alpha +\eta }$ for some $\eta >0$, and the Ring-LWE problem over $\mathcal {R}$ with standard deviation $\sigma$ is $(\varepsilon ',t')$-hard, then the above signature scheme is $(t,q_h,q_s,\varepsilon )$-unforgeable against chosen-message attacks in the random oracle model for:

$$\begin{aligned} t&\approx t' - O(q_s\cdot t_1) \\ \varepsilon&= \varepsilon ' + (q_h+q_s)\cdot \hbox {negl}(n) \end{aligned}$$

(where $t_1$ is the cost of a multiplication in $\mathcal {R}$), and it outputs a valid signature with probability $\ge 1-\big (1-1/e^2+2/(en)\big )^\ell$. If, moreover, $p \gg \sigma ^{2/\alpha }\cdot n^{4/\alpha +\eta }$ for some $\eta >0$, the signature scheme is $(t,q_h,q_s,\varepsilon )$ strongly unforgeable against chosen-message attacks.

Corollary 2

The conclusion still holds when the condition on $p$ is relaxed to $p \gg \sigma ^{2}\cdot n^{3+\eta }$ (resp. $p\gg \sigma ^2\cdot n^{4+\eta }$) for some $\eta >0$.

Proof

It suffices to apply the previous result with $\alpha$ sufficiently close to $1$. $\square$

6 A Signature Scheme Based on Subset Sum

In this section, we construct a lossy identification scheme based on the hardness of the random $\text{ SS }(n,M)$ problem for a prime $M>(2kn+1)^n\cdot 3^{2k}$, where $k$ is a security parameter. The secret key is a random matrix $\mathbf{X}\overset{\$}{\leftarrow }\{0,1\}^{n\times k}$, and the public key consists of a vector $\mathbf{a}\overset{\$}{\leftarrow }\mathbb {Z}_M^n$, and a vector $\mathbf{t}=\mathbf{a}^T\mathbf{X}\mod M$. In the first step of the protocol, the prover selects a vector $\mathbf{y}\overset{\$}{\leftarrow }\{-kn,\ldots ,kn\}^n$ and sends an integer commitment $u=\langle \mathbf{a},\mathbf{y}\rangle \mod M$ to the verifier. The verifier selects a random challenge vector $\mathbf{c}\overset{\$}{\leftarrow }\{0,1\}^k$ and sends it to the prover, who checks that $\mathbf{c}$ is indeed a valid challenge vector. The prover then computes a possible response $\mathbf{z}=\mathbf{X}\mathbf{c}+\mathbf{y}$ (note that there is no modular reduction here) and sends it to the verifier if it is in the range $\{-kn+k,\dots ,kn-k\}^n$. If $\mathbf{z}$ is not in this range, then the prover sends $\bot$. Upon receiving a $\mathbf{z}$, the verifier accepts the interaction if $\mathbf{z}\in \{-kn+k,\dots ,kn-k\}^n$ and $\langle \mathbf{a},\mathbf{z}\rangle - \langle \mathbf{t},\mathbf{c}\rangle \mod M = u$.

It is easy to see that in the case that the prover does not send $\bot$, he will be accepted by the verifier since

$$\begin{aligned} \langle \mathbf{a},\mathbf{z}\rangle - \langle \mathbf{t},\mathbf{c}\rangle \mod M = \mathbf{a}^T\mathbf{X}\mathbf{c}+\langle \mathbf{a},\mathbf{y}\rangle - \mathbf{a}^T\mathbf{X}\mathbf{c}\mod M= u. \end{aligned}$$

Then, we observe that for any element $\bar{\mathbf{z}}\in \{-kn+k,\dots ,kn-k\}^n$, the probability that the response will be $\mathbf{z}=\bar{\mathbf{z}}$ is

$$\begin{aligned} \Pr [\mathbf{z}=\bar{\mathbf{z}}]=\Pr [\mathbf{y}=\bar{\mathbf{z}}-\mathbf{X}\mathbf{c}]=1/\left| \{-kn,\ldots ,kn\}^n\right| , \end{aligned}$$

since all the coefficients of the vector $\mathbf{X}\mathbf{c}$ have absolute value at most $k$. Therefore, every element $\mathbf{z}$ in the set $\{-kn+k,\dots ,kn-k\}^n$ has an equal probability of being outputted and the probability that $\mathbf{z}\ne \bot$ is

$$\begin{aligned} \rho =\left| \{-kn+k,\ldots ,kn-k\}^n\right| /\left| \{-kn,\ldots ,kn\}^n\right| \approx (1-1/n)^n \approx 1/e. \end{aligned}$$

And thus the simulatability property of the scheme is satisfied since one can create a valid transcript by generating $(\bot ,\bot ,\bot )$ with probability $1-\rho$, and otherwise pick a random $\mathbf{z}\in \{-kn+k,\dots ,kn-k\}^n$, a random $\mathbf{c}\in \{0,1\}^k$, and output $(\langle \mathbf{a},\mathbf{z}\rangle - \langle \mathbf{t},\mathbf{c}\rangle \mod M,\mathbf{c},\mathbf{z})$.

The lossy public keys are just two uniformly random vectors $\mathbf{a}$ and $\mathbf{t}$, and so, the indistinguishability of these keys from the real keys is directly based on the hardness of the $\text{ SS }(n,M)$ problem using a standard hybrid argument.

To show lossiness, we observe that if $\mathbf{t}$ is uniformly random in $\mathbb {Z}_M^k$, then it can be shown that with high probability, for any choice of $u\in \mathbb {Z}_M$, there is at most one value $\mathbf{c}$ such that $u$ can be written as $\langle \mathbf{a},\mathbf{z}\rangle - \langle \mathbf{t},\mathbf{c}\rangle \mod M$. Indeed, if there exist two pairs $(\mathbf{z},\mathbf{c}), (\mathbf{z}',\mathbf{c}')$, such that

$$\begin{aligned} \langle \mathbf{a},\mathbf{z}\rangle - \langle \mathbf{t},\mathbf{c}\rangle = \langle \mathbf{a},\mathbf{z}'\rangle - \langle \mathbf{t},\mathbf{c}' \rangle \mod M, \end{aligned}$$

then we have

$$\begin{aligned} \langle \mathbf{a},\mathbf{z}-\mathbf{z}'\rangle - \langle \mathbf{t},\mathbf{c}-\mathbf{c}' \rangle \mod M=0. \end{aligned}$$

(2)

The set of valid pairs $(\mathbf{z}-\mathbf{z}',\mathbf{c}-\mathbf{c}')$ consists of $(2kn+1)^n\cdot 3^k$ elements. If $(\mathbf{a},\mathbf{t})$ is chosen completely at random, then for each of those valid pairs, the probability that Eq. (2) is satisfied is $1/M$ (since $(\mathbf{z},\mathbf{c})\ne (\mathbf{z}',\mathbf{c}')$ and $M$ is prime) and so the probability over the randomness of $\mathbf{a}$ and $\mathbf{t}$ that Eq. (2) is satisfied for any of the valid pairs is at most $(2kn+1)^n\cdot 3^k/M$, which by our choice of $M$ is at most $3^{-k}$. A similar argument also shows that the identification scheme is unique with respect to lossy keys, in the sense of Definition 7, so that the corresponding signature scheme is strongly unforgeable.

To convert this lossy identification scheme to a signature scheme, one would simply perform the transformation described in Fig. 1, as we did for the other schemes in this paper. And as for the lattice-based scheme in Sect. 5, we point out that the technique in [39] can be used to reduce the coefficients of the signature by about a factor of $\sqrt{n}$ to make them fall in the range $\{-O(k\sqrt{n}),\dots ,O(k\sqrt{n})\}^n$ by sampling the vector $\mathbf{y}$ from a normal distribution and performing a somewhat more involved rejection sampling procedure when deciding whether or not to send the response $\mathbf{z}$. This would also allow us to reduce the modulus $M$ to approximately $M=O(k\sqrt{n})^n\cdot 3^{2k}$, which makes the $\text{ SS }(n,M)$ problem more difficult. Another possible optimization could include making $k$ larger, but making the vector $\mathbf{c}$ sparser (while still making sure that it comes from a large enough set), which would result in a shorter vector $\mathbf{X}\mathbf{c}$.

We would also like to point out that one could also construct the scheme above based on the subset sum assumption over $\mathbb {Z}^m_q$, rather than over $\mathbb {Z}_M$, for parameters $m$ and $q$ for which the corresponding vector subset sum problem is hard. The proof details would be almost the same. One would just have to change $\mathbf{a}$ from being an $n$-dimensional vector to an $m\times n$-dimensional matrix, and similarly change $\mathbf{t}$ from a $k$-dimensional vector to an $m\times k$-dimensional matrix. Then, all that is left to do is to verify that for the chosen parameters, the probability of Eq. (2) being $0$ over the random choices of $\mathbf{a}$ and $\mathbf{t}$ remains small.

Appendices

Appendix 1: Technical Lemmas for the Lattice-Based Scheme

Lemma 4

If $\mathbf{s}\overset{\$}{\leftarrow }D_{\mathcal {R},\sigma }$ and $\mathbf{c}\overset{\$}{\leftarrow }\mathcal {C}$, then

$$\begin{aligned} \Pr \left[ \Vert \mathbf{s}\mathbf{c}\Vert _\infty \le \sigma \sqrt{n}\log ^3{n}\right] =1-e^{-\varOmega (\log ^2{n})}. \end{aligned}$$

Proof

Since each coefficient of $\mathbf{s}$ is sampled from $D_{\mathbb {Z},\sigma }$, we know (for example, by using [27, Lemma 4.2] and the union bound) that the probability that $\Vert \mathbf{s}\Vert _\infty >\sigma \log {n}$ is $e^{-\varOmega (\log ^2{n})}$. Now observe that if we write $\mathbf{s}=\sum _{i=0}^{n-1}{s_i\mathbf{x}^i}$ and $\mathbf{c}=\sum _{i=0}^{n-1}{c_i\mathbf{x}^i}$, then the $\mathbf{x}^j$th coefficient of $\mathbf{s}\mathbf{c}$ is equal to $\sum _{i=0}^{j}{c_is_{j-i}}-\sum _{i=j+1}^{n-1}{c_{i}s_{n+j-i}}$. Because all the coefficients $c_i$ are randomly and independently chosen integers from the range $[-\log {n},\log {n}]$, the coefficients $c_is_j$ are independent random variables in the range $[-\sigma \log ^2{n},\sigma \log ^2{n}]$ with mean $0$, and so every coefficient of $\mathbf{s}\mathbf{c}$ is a sum of $n$ such values. By applying the Hoeffding inequality and the union bound over all the coefficients of $\mathbf{s}\mathbf{c}$, we obtain the claim in the statement of the lemma. $\square$

Lemma 5

If $\mathbf{r}\in \mathcal {R}$ is any polynomial such that $\Vert \mathbf{r}\Vert _\infty \le \sigma \sqrt{n}\log ^3{n}$, then for every element $\mathbf{g}\in \mathcal {G}$,

$$\begin{aligned} \mathop {\hbox {Pr}}\limits _{\mathbf{y}\overset{\$}{\leftarrow }\mathcal {M}}[\mathbf{r}+\mathbf{y}=\mathbf{g}]=1/|\mathcal {M}|. \end{aligned}$$

Proof

We have:

$$\begin{aligned} \mathop {\hbox {Pr}}\limits _{\mathbf{y}\overset{\$}{\leftarrow }\mathcal {M}}[\mathbf{r}+\mathbf{y}=\mathbf{g}]=\mathop {\hbox {Pr}}\limits _{\mathbf{y}\overset{\$}{\leftarrow }\mathcal {M}}[\mathbf{y}=\mathbf{g}-\mathbf{r}]=1/|\mathcal {M}|, \end{aligned}$$

where the last equality is true because for all $\mathbf{r}$ and $\mathbf{g}$ defined as in the statement of the lemma, $\mathbf{g}-\mathbf{r}\in \mathcal {M}$. $\square$

Proof of Lemma 3

By Lemma 4, we know that $\Pr [\Vert \mathbf{s}\mathbf{c}\Vert _\infty \le \sigma \sqrt{n}\log ^3{n}]=1-e^{-\varOmega (\log ^2{n})}$, and in this case, Lemma 5 tells us that for any $\mathbf{g}\in \mathcal {G}, \Pr [\mathbf{s}\mathbf{c}+\mathbf{y}=\mathbf{g}]=1/|\mathcal {M}|$. Putting this all together, we get

$$\begin{aligned}&\Pr [\mathbf{s}\mathbf{c}+\mathbf{y}\in \mathcal {G}]\ge \left( 1-e^{-\varOmega (\log ^2{n})}\right) \cdot \frac{|\mathcal {G}|}{|\mathcal {M}|}\ge \left( 1-e^{-\varOmega (\log ^2{n})}\right) \cdot \left( 1-\frac{1}{n}\right) ^n\\&\quad \ge \frac{1}{e}-\frac{1}{en}-e^{-\varOmega (\log ^2{n})} \end{aligned}$$

which is the first stated result. Similarly, we obtain:

$$\begin{aligned} \Pr [\mathbf{s}\mathbf{c}+\mathbf{y}\in \mathcal {G}]\le \left( 1-e^{-\varOmega (\log ^2{n})}\right) \cdot \frac{|\mathcal {G}|}{|\mathcal {M}|} + e^{-\varOmega (\log ^2{n})} \le \frac{|\mathcal {G}|}{|\mathcal {M}|} + e^{-\varOmega (\log ^2{n})} \end{aligned}$$

and for the same reasons, we have for any $\mathbf{g}\in \mathcal {G}$:

$$\begin{aligned} \left( 1-e^{-\varOmega (\log ^2{n})}\right) \cdot \frac{1}{|\mathcal {M}|}\le \Pr [\mathbf{s}\mathbf{c}+\mathbf{y}=\mathbf{g}]\le \frac{1}{|\mathcal {M}|} \end{aligned}$$

where the latter inequality holds because clearly, the probability over the choice of $\mathbf{y}$ that $\mathbf{y}= \mathbf{g}-\mathbf{s}\mathbf{c}$ can never exceed $1/|\mathcal {M}|$. Hence, we can bound the conditional probability

$$\begin{aligned} \Pr [\mathbf{s}\mathbf{c}+\mathbf{y}= \mathbf{g}\ |\ \mathbf{s}\mathbf{c}+\mathbf{y}\in \mathcal {G}] = \frac{\Pr [\mathbf{s}\mathbf{c}+\mathbf{y}= \mathbf{g}]}{\Pr [\mathbf{s}\mathbf{c}+\mathbf{y}\in \mathcal {G}]} \end{aligned}$$

as follows:

$$\begin{aligned} \frac{\frac{1}{|\mathcal {M}|}\big (1-e^{-\varOmega (\log ^2{n})}\big )}{\frac{|\mathcal {G}|}{|\mathcal {M}|} + e^{-\varOmega (\log ^2{n})}}&\le \Pr [\mathbf{s}\mathbf{c}+\mathbf{y}= \mathbf{g}\ |\ \mathbf{s}\mathbf{c}+\mathbf{y}\in \mathcal {G}] \le \frac{\frac{1}{|\mathcal {M}|}}{\frac{|\mathcal {G}|}{|\mathcal {M}|}\big (1-e^{-\varOmega (\log ^2{n})}\big )} \\ \frac{1}{|\mathcal {G}|}\cdot \frac{1-e^{-\varOmega (\log ^2{n})}}{1+\frac{|\mathcal {M}|}{|\mathcal {G}|}e^{-\varOmega (\log ^2{n})}}&\le \Pr [\mathbf{s}\mathbf{c}+\mathbf{y}= \mathbf{g}\ |\ \mathbf{s}\mathbf{c}+\mathbf{y}\in \mathcal {G}] \le \frac{1}{|\mathcal {G}|}\cdot \frac{1}{1-e^{-\varOmega (\log ^2{n})}} \\ \frac{1}{|\mathcal {G}|}\cdot \left( 1-2\frac{|\mathcal {M}|}{|\mathcal {G}|}e^{-\varOmega (\log ^2{n})}\right)&\le \Pr [\mathbf{s}\mathbf{c}+\mathbf{y}= \mathbf{g}\ |\ \mathbf{s}\mathbf{c}+\mathbf{y}\in \mathcal {G}] \le \frac{1}{|\mathcal {G}|}\cdot \left( 1+2e^{-\varOmega (\log ^2{n})}\right) . \end{aligned}$$

As a result, we obtain the desired bound:

$$\begin{aligned} \sum _{\mathbf{g}\in \mathcal {G}} \left| \Pr [\mathbf{s}\mathbf{c}+\mathbf{y}= \mathbf{g}\ |\ \mathbf{s}\mathbf{c}+\mathbf{y}\in \mathcal {G}] - \frac{1}{|\mathcal {G}|} \right| \le |\mathcal {G}|\cdot \frac{e^{-\varOmega (\log ^2{n})}}{|\mathcal {G}|} = e^{-\varOmega (\log ^2{n})}. \end{aligned}$$

$\square$

Proof of Lemma 2

First fix a divisor $Q$ of degree $d$ of $\mathbf{x}^n+1$ in $\mathbb {Z}_p[\mathbf{x}]$, and write $\mathbf{x}^n+1 = Q\cdot \tilde{Q}$. Since $\mathbf{x}^n+1$ is separable, $Q$ and $\tilde{Q}$ are coprime, so that any element $\mathbf{t}\in \mathcal {R}$ is entirely determined by its reductions mod $Q$ and $\tilde{Q}$.

Now, let us first estimate the number of elements $\bar{\mathbf{t}}\in \mathcal {R}/\langle Q\rangle$ such that there exists $(\mathbf{z}_1,\mathbf{z}_1',\mathbf{z}_2,\mathbf{z}_2')\in \mathcal {G}^4$ and $(\mathbf{c},\mathbf{c}')\in \mathcal {C}^2$ with $\mathbf{c}-\mathbf{c}'$ invertible mod $Q$ such that:

$$\begin{aligned} \frac{\mathbf{a}(\mathbf{z}_1-\mathbf{z}_1') + (\mathbf{z}_2-\mathbf{z}_2')}{\mathbf{c}-\mathbf{c}'} \mod Q = \bar{\mathbf{t}}. \end{aligned}$$

(3)

Since $\Vert \mathbf{z}_i-\mathbf{z}_i'\Vert _\infty \le 2(n-1)\sqrt{n}\sigma \log ^3{n}$ for $i=1,2$, there are at most $\big (4(n-1)\sqrt{n}\sigma \log ^3{n} + 1\big )^n$ elements of $\mathcal {R}$ of the form $\mathbf{z}_i-\mathbf{z}_i'$. Similarly, there are at most $\big (2\log {n}+1\big )^n$ elements of the form $\mathbf{c}-\mathbf{c}'$. Hence, the number of $\bar{\mathbf{t}}\in \mathcal {R}/\langle Q\rangle$ that can be written as the ratio (3) is at most:

$$\begin{aligned} \big (4(n-1)\sqrt{n}\sigma \log ^3{n} + 1\big )^{2n}\cdot \big (2\log {n}+1\big )^n \le \big (33n^3\sigma ^2\log ^7{n}\big )^n. \end{aligned}$$

Then, if we consider instead the elements $\mathbf{t}\in \mathcal {R}$ that can be written in the form (1), there are at most $\big (33n^3\sigma ^2\log ^7{n}\big )^n$ choices for their reduction mod $Q$, and all the possible choices, namely $p^{n-d}$, for their reduction mod $\tilde{Q}$. This bounds their number as $p^{n-d}\cdot \big (33n^3\sigma ^2\log ^7{n}\big )^n$ for any fixed choice of the degree-$d$ divisor $Q$ of $\mathbf{x}^n+1$.

Since $\mathbf{x}^n+1$ splits completely in $\mathbb {Z}_p$, it has exactly $\left( {\begin{array}{c}n\\ d\end{array}}\right)$ divisors of degree $d$. Thus, we obtain the required estimate for the probability of being an $\alpha$-partial modular ratio:

$$\begin{aligned}&\Pr [ \mathbf{t}\text { is an }\alpha -\text {partial modular ratio} ] \le \frac{1}{p^n} \cdot \left( {\begin{array}{c}n\\ d\end{array}}\right) \cdot p^{n-d} \cdot (33n^3\sigma ^2\log ^7{n})^n \\&\quad = \left( {\begin{array}{c}n\\ d\end{array}}\right) \left( \frac{33n^3\sigma ^2\log ^7{n}}{p^\alpha }\right) ^n. \end{aligned}$$

To see that this is negligible as soon as $p\gg n^{3/\alpha +\eta }$, we only need to find an asymptotic estimate of the binomial coefficient. But by the Stirling formula, we have:

$$\begin{aligned} \left( {\begin{array}{c}n\\ d\end{array}}\right) \sim \frac{1}{\sqrt{2\pi \cdot \alpha (1-\alpha ) n}} \left( \frac{1}{\alpha ^\alpha (1-\alpha )^{1-\alpha }}\right) ^n. \end{aligned}$$

Therefore, we obtain:

$$\begin{aligned} \Pr [ \mathbf{t}\text { is an }\alpha -\text {partial modular ratio} ] \ll \left( \frac{33n^3\sigma ^2\log ^7{n}}{\alpha ^\alpha (1-\alpha )^{1-\alpha }\cdot p^\alpha }\right) ^n \end{aligned}$$

which is indeed negligible if $p \gg \sigma ^{2/\alpha }\cdot n^{3/\alpha +\eta }$, for any $\eta >0$. $\square$

Appendix 2: Min-Entropy

Let $\mathsf {ID}=({\mathsf {KeyGen}},{\mathsf {LosKeyGen}},{\mathsf {Prove}},c,{\mathsf {Verify}})$ be a lossy identification scheme. Let $k\in {{\mathbb N}}$, and let $(pk,sk)$ be a key pair generated by ${\mathsf {KeyGen}}$ on input $k$. Let $\mathcal {C}(sk) = \{{\mathsf {Prove}}(sk;R_P): R_P\in {\mathsf {Coins}}_{{\mathsf {Prove}}}(k) \}$ be the set of commitments associated to $sk$. As in [1], we define the maximum probability that a commitment takes on a particular value via

$$\begin{aligned} \alpha (sk)={\displaystyle {\mathop {\mathrm {max}}_{cmt\in \mathcal {C}(sk)}}\left\{ {\Pr }\left[ \, {\mathsf {Prove}}(sk;R_P)=cmt\,\,:\,\,R_P\overset{\$}{\leftarrow }{\mathsf {Coins}}_{{\mathsf {Prove}}}(k)\,\right] \right\} }. \end{aligned}$$

Then, the min-entropy function associated with $\mathsf {ID}$ is defined as follows:

$$\begin{aligned} \beta (k) = {\displaystyle {\mathop {\mathrm {min}}_{sk}}\left\{ \log _{2}{\frac{1}{\alpha (sk)}} \right\} } \;, \end{aligned}$$

where the minimum is over all $(pk,sk)$ generated by ${\mathsf {KeyGen}}$ on input $k$.