High-sensitivity analysis of polarization by surface reflection

Abstract

The exploitation of polarization information in the field of computer vision has become progressively more popular during the last few decades. This is primarily due to (1) the fact that polarization is a source of mostly untapped information for machine vision; (2) the relative computational ease by which geometrical information about a scene (e.g. surface normals) may be extracted from polarization data; and (3) the recent introduction of camera hardware able to capture polarization data in real time. The motivation for this paper is that a detailed quantitative study into the precision of polarization measurements with respect to expectation has yet to be performed. The paper therefore presents a detailed analysis and optimization of the key aspects of data capture necessary to acquire the most precise (as opposed to fast) results for the benefit of future research into the field of “polarization vision.” The paper mainly focuses on a rotating polarizer method as this is shown to be the most accurate for high-sensitivity measurements. Commercial polarization cameras by contrast generally sacrifice precision for the benefit of much shorter capture times. That said, the paper reviews the state of the art in polarization camera technology and quantitatively evaluates the performance of one such camera: the Fraunhofer “POLKA.”

1 Introduction

Many areas of technology exploit the polarization state of light in order to extract or visualize useful information about a scene or object under scrutiny. Areas of interest are vast and range from entertainment (e.g. 3D cinema) to industrial inspection [14, 32, 41]. The field of “polarization vision” may be defined as the acquisition and use of images that encode information about the polarization state of incoming light. The polarization state of light is typically represented either by the Stokes vector or phase (angle) and degree of polarization. An image containing these data independently for each pixel may be termed a “polarization image.” Note that this contains very different information to a standard image, which only represents the intensity of light entering the camera. Researchers in computer vision have exploited this novel information for applications such as three-dimensional object reconstruction and image enhancement, as explained in Sect. 2.2.

Unfortunately, polarization images are often time-consuming to acquire and/or have low signal-to-noise ratios. As will be explained in the next section, many recent developments in the field have reduced the capture time but involve expensive hardware and still result in relatively noisy images when the incident polarization is low. However, many polarization vision methods require very high sensitivity measurements such as those involving diffuse surface reflection [3] or scattering in the atmosphere [40] or seawater [39]. The motivation for this work is therefore the need to optimize data capture for such applications where highly sensitive measurements are required.

In this paper, all of the key image acquisition parameters required for high-sensitivity polarization image acquisition are considered in order to obtain a recommendation for any further research into polarization vision. The tests were carried out using a custom-made rig consisting of a motor-controlled polarizing filter in front of a standard machine vision camera. Illumination was carefully controlled to ensure fairness of comparisons and repeatability. Most of the tests are carried out on a white snooker ball due to it’s precision surface, known geometry and full range of surface normals. This work also tests the resulting optimized system in a series of experiments that require measurements with very low levels of polarization—namely, that of diffusely reflected light. Finally, the paper is able to verify a range of specular and diffuse reflection phenomena that are ubiquitous in nature and so need to be fully understood for future polarization vision applications (e.g. in robotics). The results of this paper therefore offer major benefits for future work in high-sensitivity polarization analysis for many applications of polarization vision, while contributing to our understanding of reflectance-induced polarization in real-world data.

In summary, the focus of this paper is on the capture optimization and image understanding that pertains to many of the polarization-based vision applications listed in the next section. The contributions are as follows:

• Optimization of image capture conditions for sensitive polarization imaging application.

• Quantification of the performance of image capture for the specific hardware used.

• Qualitative study of various polarization phenomena using the optimal conditions that have typically been overlooked in most previous works.

Section 2 of this paper reviews the literature in this area of research both from an image acquisition and application perspective. Related optics theory relating to reflectance and polarization data representation is furnished in Sect. 3. The numerous parameters of polarization image acquisition are quantitatively studied and compared to theory in Sect. 4, with key recommendations clearly summarized. Section 5 presents an analysis of the images in more complicated conditions, such as those with inter-reflections and rough surfaces. Finally, Sect. 6 concludes the paper and points towards future work and opportunities. Most data used for this paper can be downloaded from http://researchdata.uwe.ac.uk/244/.

2 Related work

This section first considers the various methods and hardware for polarization image capture before reviewing the state-of-the-art applications in the field of computer vision.

2.1 Data acquisition

The most basic method for data capture (covered in detail in Sects. 3 and 4) relies on taking multiple images of the target object/scene as a polarizer in front of a standard camera is rotated. A minimum of three images are necessary assuming there is no circular polarization present. While it is relatively straightforward to motorize the rotation, the need for images with multiple polarizer angles limits applications to static scenes: a clear drawback of the method.

In the late 1990s, capture time was improved considerably by the development of polarization cameras [56] that used liquid crystals to rapidly switch the axis of the polarizing filter. The disadvantage here is that the data have a high susceptibility to noise. Further, while the need for mechanical rotation was diminished, the capture time is still slower than a standard camera. Polarized lead zirconium titanate (PLZT) [43] was also used for a similar purpose, which could be applied to recover all four components of the Stokes vector [19, 26]. The commercial “SALSA” camera from Bossa Nova Technologies [7] uses ferroelectric liquid crystals in front of the lens/sensor. This offers somewhat faster acquisition but is still of insufficient frame rate for many applications. However, their method allows full recovery of Stokes parameters.

An alternative approach uses a type of beam splitter to project the image onto several (usually four) separate cameras, each of which is equipped with a polarization filter at a different angle [15, 34, 47, 55]. This eliminates the problem of motion artefacts, but such an arrangement is expensive and difficult to calibrate since all four cameras need be aligned. Another problem is light sensitivity: Beam splitters divide the incoming light into a separate beam for each camera losing intensity in the process. Each beam then loses more light still as it passes the filter. On the other hand, this technology has been applied to recover full Stokes parameters by using retarders to recover elliptical polarization. These retarders have to be switched (e.g. [7]) or there needs to be at least two different retarders in the optical paths of the camera (e.g. [34]).

Several cameras that overcome some of the above issues have emerged that incorporate filters onto the sensor chip [1, 35, 49]. A pixel-by-pixel polarization filter is designed and then usually put on an existing image sensor using transparent adhesives. This has the advantage of eliminating motion artefacts and enabling one to use a “normal” camera that may be small and robust. However, the design and fabrication of such polarization filters is expensive and the process of putting them onto an existing sensor is difficult and, again, costly. Another problem is the behaviour of the adhesives used: Usually they expand or contract when the temperature changes, which influences the filter’s alignment on the pixels. In addition, the pixels need to be relatively large for this to work, so it is difficult to implement for high-resolution sensors, which usually have small pixels. In related work, Momeni and Titus [28] use microfilters with two photodiodes per pixel to build a sensor inspired by the photoreceptors on an octopus retina.

The “POLKA” camera, which also uses microfilters, contains a special CMOS imager developed by the Fraunhofer Institute for Integrated Circuits [13, 21]. This time, however, the filters are integrated onto the pixels themselves. In this sensor, miniaturized wire-grid polarization structures are put directly into the pixels in a regular CMOS fabrication process. Four different polarizer angles of $0^{\circ }$, $45^{\circ }$, $90^{\circ }$ or $135^{\circ }$ are arranged in groups of $2\times 2$ pixels, from which the first three Stokes parameters are calculated in a similar fashion to the rotating polarizer method. A recent development from Sony involves a similar microfilter array but also using micro-lenses for each pixel [46].

Tokuda et al. [50] used the same principle as POLKA to realize polarization filters in a CMOS imager. The pixels are very large ($200 \times 200\,\upmu \hbox {m}$) and show good polarization effectivity. The sensor consists of 12 pixels with different filter orientations and does not deliver an image, but has proven useful for measuring the concentration of a sucrose solution. Since the polarization-dependent sensitivity decreases with smaller pixels, it seems difficult to shrink the pixel size significantly to get a substantial image with hundreds kilopixels or more.

Gruev et al. [18] combined polymer polarization filters with a CMOS image sensor by using a special microfabrication procedure. The sensor delivers data to compute the first three Stokes parameters in a similar way the POLKA. Since the thickness of the polymer filters is about 25µm, there is significant optical cross talk to neighbour pixels when the light beam in not exactly parallel to the optical axis. The so-called chief ray angle is normally more than ten degrees, depending on the distance to the optical axis, and so the cross talk varies from the centre to the corners of the image. It is difficult to correct for this effect by means of image processing and is different for each type of lens used so must be corrected individually. Since the fabrication of the filters is an additional and expensive step, it is not possible to produce polarization image sensors for the mass market.

Wu et al. [59] realized a $2\times 2$ wire-grid polarizer filter mosaic targeted at the visible spectrum and fabricated this into a 65nm standard CMOS processing line. A polarization extinction ratio around 10 is achieved with a pixel size of $12\times 12\,\upmu \hbox {m}$. Instead of metal micro-grid polarizers, Zhao et al. [61] used the well-controlled process of ultraviolet photolithography to define micropolarizer orientation patterns on a spin-coated azo-dye-1 film. It exhibits a relatively good extinction ratio of about 100, which minimizes the need for complicated correction algorithms to get accurate Stokes parameters. A comparison to the work of Gruev et al. is made concerning the thickness of the micropolarizers and the corresponding problem with cross talk, which is much lower with the very thin azo-dye-1.

Finally, Yamazaki et al. [60] fabricated an air-gap wire-grid polarizer that achieved a transmittance of 63.3% and an extinction ratio of 85 at $550\,\upmu \hbox {m}$ using a very fine $150\,\upmu \hbox {m}$ metal pitch. The pixel size of $2.5\times 2.5\,$µm enables the production of megapixel sensors with reasonable chip size. This means that standard lenses can be used and production costs are kept relatively low.

2.2 Applications

Polarization vision taps into an entire set of information about the incoming light that a standard monochrome or RGB camera is unable to access. Thus, it may be argued that a great deal of potentially useful information about the incoming light is lost in standard vision techniques. Of course, the additional information available from polarization imaging systems comes at the cost of more expensive and often slower capture hardware. This section primarily focuses on shape recovery methods that use this additional source of information. A variety of other application areas are also briefly considered.

2.2.1 Shape analysis

The most relevant related work in polarization vision uses Fresnel theory applied to specular reflection [19]. The theory tells us that initially unpolarized illumination undergoes a partial linear polarization process upon reflection from surfaces. The specific properties of the polarization correlate with the relationship between the surface orientation and the viewing direction [38, 57]. This theoretically allows for three-dimensional shape estimation. Unfortunately, there are inherent ambiguities present and the refractive index of the target is typically required in order to reliably estimate the surface geometry (orientation) at each point. Further, different equations are required to model reflection if a diffuse component is present.

Miyazaki et al. [25], Atkinson and Hancock [4] and Berger et al. [6] all used multiple viewpoints to overcome the ambiguity issue. In [25], specular reflection was used on transparent objects—a class of material that causes difficulty for most computer vision methods. In [4], a patch matching approach was used for diffuse surfaces to find stereo correspondence and, hence, 3D data. In [6], an energy functional for a regularization-based stereo vision was applied. Taamazyan et al. [48] used a combination of multiple views and a physics-based reflection model to simultaneously separate specular and diffuse reflection and estimate shape (Miyazaki et al. [27] also separated reflection components but only as a preprocessing step).

Drbohlav and Šára [11, 12] used multiple linearly polarized light source imaging to overcome ambiguities and determine shape. Atkinson and Hancock [5] applied multiple highly controlled but unpolarized illumination sources. Later, Atkinson [2] extended the method to account for inter-reflections and weak specularities. More recently, Ngo et al. [31] also used multiple-light polarization imaging. Garcia et al. [17] used a circularly polarized light source to overcome the ambiguities while Morel et al. [29] extended the methods of polarization to metallic surfaces by allowing for a complex index of refraction. Smith et al. [45] assumed a known and constant refractive index and albedo but are able to pose the problem as a system of linear equations. This permits direct determination of depth up to a concave/convex ambiguity in the presence of both diffuse and specular reflection.

In an effort to overcome the need for the refractive index, Miyazaki et al. constrained the histogram of surface normals [27] while Rahmann and Canterakis [36, 37] used multiple views and the orientation of the plane of polarization for correspondence. Huynh et al. [20] actually estimated the refractive index using spectral information. Kadambi et al. [22] proposed a method to allow polarization information to be combined with alternative depth capture methods resulting in overall improved reconstructions.

2.2.2 Other applications

Wallace et al. used polarization to improve depth estimation from laser range scanners [53]. Traditional techniques in the field encounter difficulty when scanning metallic surfaces due to inter-reflections. In the Wallace et al. paper, the problems were reduced by calculating all four Stokes parameters to differentiate direct laser reflections from inter-reflections.

Nayar et al. noted that consideration of colour shifts upon surface reflection, in conjunction with polarization analysis, can be used to separate specular and diffuse reflections [30]. Umeyama later used a different method to achieve the same goal using only polarization [52].

Shibata et al. [44] and Atkinson and Hancock [5] used polarization filtering as part of a reflectance function estimation technique, while Chen and Wolff [9] segmented images by material type (metallic or dielectric). Schechner et al. showed how polarization can enhance images taken through haze [40] before later extending the work to marine imagery [39].

Finally, polarization was recently used by Schöberl et al. for automated inspection of carbon fibre components [41]. They make use of the fact that such components reflect light with an electric field oriented parallel to the fibres and hence allow for gaps and poorly oriented threads to be identified.

2.3 Discussion

Section 2.2 clearly demonstrates the wide-ranging potential for polarization vision. However, despite advances in hardware methods, as discussed in Sect. 2.1, it remains difficult to outperform the basic rotating polarizer method in terms of precision alone (as opposed to usefulness, where many of the newer systems are superior due to higher-speed operation). The reason for this is, essentially, that the rotating polarizer method allows for the use of a separate high-quality camera and filter without the complications of pixel-level fabrication processes. Nevertheless, there remains a host of factors that determine the precision of measurements using this well-established approach, and this paper aims to optimize each of these to enable the highest sensitivity measurements to be made.

3 Polarization theory

The two most common causes of spontaneous polarization in nature are reflection/refraction and scattering. This paper is primarily concerned with the former, although most of the methods for data capture relate equally to any form of incoming polarized light. The goal of polarization vision is to analyse incoming light and fully parametrize its polarization state for each pixel in an image or video.

3.1 Representation

The polarization state of light can be fully parametrized by the Stokes vector [19]:

$$\begin{aligned} S = \left[ S_0, S_1, S_2, S_3\right] ^\mathrm{T} \end{aligned}$$

(1)

The first of the parameters of the Stokes vector, $S_0$, is simply the intensity of the light. The range and units for this may vary but for applications of polarization vision is typically normalized in the range [0, 1]. The second parameter, $S_1$, quantifies the tendency for horizontal ($S_1 > 0$) or vertical ($S_1 < 0$) polarization. For the case where $S_1 = 0$, there is no tendency either way as in circular polarized light, elliptical light at $45^{\circ }$ and unpolarized light. $S_2$ is interpreted in a similar fashion to $S_1$, but relates to angles of $45^{\circ }$ and $-\,45^{\circ }$ ($135^{\circ }$). Finally, $S_3$ relates to circular/elliptical polarization which is not common in nature. For this reason, it is assumed that $S_3=0$ throughout this paper.

While the Stokes vector is commonly used in optics, many areas of research use an alternative form based on intensity, I, phase, $\phi$, and degree of polarization, $\rho$. The chief advantage of this form is that it offers a more directly interpretable formulation. The phase angle defines the principle angle of the electric field component of the light. The degree of polarization indicates the fraction of the measured light that is polarized [19]:

$$\begin{aligned} \rho = \frac{I_p}{I_p+I_u} \end{aligned}$$

(2)

where $I_u$ is the intensity of unpolarized light and $I_p$ is that of polarized light. This means that $\rho = 0$ refers to unpolarized and $\rho =1$ refers to completely linearly polarized.

The two representations are related by the following [19]:

$$\begin{aligned} I= & {} S_0 \end{aligned}$$

(3)

$$\begin{aligned} \phi= & {} \frac{1}{2}\arctan _2\left( S_2,S_1\right) \end{aligned}$$

(4)

$$\begin{aligned} \rho= & {} \frac{\sqrt{S_1^2+S_2^2}}{S_0} \end{aligned}$$

(5)

where $\arctan _2$ is the four quadrant inverse tangent¹ [8].

3.2 Reflection theory

Assume for now that the reflecting surface is a smooth dielectric. Reflected light can be represented as a superposition of specular and diffuse reflection [42]. The specular component occurs at the surface only, while the diffuse component is the result of subsurface scattering. For the latter, assume that the Wolff reflection model applies [54], whereby electronic motions near the surface of the material give rise to the reflection following the Fresnel theory for electromagnetic wave transmission [19].

3.2.1 Specular reflection

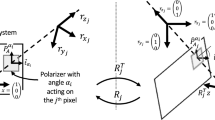
For the specular component of reflection (see the left-hand side of Fig. 1), Fresnel’s theory can be applied to directly determine the ratio of incident to reflected light. This is done separately for incident components where the electric field is parallel to ($R_{\Vert }$) or perpendicular to ($R_{\perp }$) the plane of incidence:

$$\begin{aligned} R_{\Vert }= & {} \left( \frac{n_t\cos \theta _i-n_i\cos \theta _t}{n_t\cos \theta _i+n_i\cos \theta _t}\right) ^2 \end{aligned}$$

(6)

$$\begin{aligned} R_{\perp }= & {} \left( \frac{n_i\cos \theta _i-n_t\cos \theta _t}{n_i\cos \theta _i+n_t\cos \theta _t}\right) ^2 \end{aligned}$$

(7)

The angles $\theta _i$ and $\theta _t$ are defined in Fig. 1, and $n_i$ and $n_t$ are the refractive indices of the incident and reflecting media, respectively. Since the incident medium is air, the approximation is made that $n_i=1$. The angle $\theta _t$ can be obtained using Snell’s Law:

$$\begin{aligned} n_i\sin \theta _i=n_t\sin \theta _t \end{aligned}$$

(8)

This means that the two coefficients in (6) and (7) have only two dependencies: $n_t$ and $\theta _i$.

Fig. 1

Schematic illustration of the process for specular and diffuse reflection

Examination of (6) and (7) reveals that $R_{\perp }\ge R_{\Vert }$ for all incident angles. This means that:

• specularly reflected light is generally polarized.

• the phase angle is always perpendicular to the plane of reflection.

Fig. 2

Schematic showing the variation of intensity with polarizer angle for the range $\theta _{\mathrm {pol}}\in [0^{\circ },360^{\circ }]$. $\phi$ is the phase angle, $\alpha _{1,d}$ and $\alpha _{2,d}$ are the possible azimuth angles for diffuse reflection and $\alpha _{1,s}$ and $\alpha _{2,s}$ are likewise for specular reflection

3.2.2 Diffuse reflection

According to the Wolff model [54], the scattered light just below the surface should undergo a transmission from the subsurface back into air to form the diffuse reflection, as shown in the right-hand side of Fig. 1. In such a case, the Fresnel transmission coefficients ($T_{\Vert }=1-R_{\Vert }$ and $T_{\perp }=1-R_{\perp }$) are applied to determine the relative contributions of the parallel and perpendicular components of the light. In this case, the incident angle and refractive index relate to the reflecting medium and the transmitted values are for air. Snell’s law (8) can be used to interchange between incident angle (here the uninformative $\theta _i'$) and the more useful emittance angle ($\theta _t'$), in a similar fashion to earlier.

Examination of the Fresnel transmission coefficients [3] reveals that $T_{\Vert }\ge T_{\perp }$ for all emittance angles. This means that:

• diffusely reflected light is generally polarized.

• the phase angle is always equal to the angle of the plane of reflection.

3.3 Polarization analysis

This section considers how the reflectance phenomena discussed above can be analysed in order to represent the polarization state of the reflected light in an image. Consider a field of partially polarized light directed towards a camera with a linear polarizer placed in front of the lens. If the phase angle of the light at a particular point relative to a horizontal reference angle is $\phi$ and the transmission axis of the linear polarizer is $\theta _{\mathrm {pol}}$, then the intensity of light emerging from the other side of the polarizer is given by the transmitted radiance sinusoid (TRS) [3, 55]:

$$\begin{aligned} I_{\mathrm {pol}}\left( \theta _{\mathrm {pol}},\phi \right) = \frac{I_{\max }+I_{\min }}{2} + \frac{I_{\max }-I_{\min }}{2}\cos \left( 2\theta _{\mathrm {pol}}-2\phi \right) \end{aligned}$$

(9)

where $I_{\max }$ and $I_{\min }$ are transmitted intensities when $\theta _{\mathrm {pol}}=\phi$ and $\theta _{\mathrm {pol}}=\phi \pm 90^{\circ }$, respectively. This relationship is illustrated by the graph in Fig. 2.

Assume now that light measured at a particular location has undergone specular reflection. Using the theory from Sect. 3.2.1:

$$\begin{aligned} I_{\max }= \frac{R_{\perp }}{R_{\perp }+R_{\Vert }}I;\qquad I_{\min }= \frac{R_{\Vert }}{R_{\perp }+R_{\Vert }}I \end{aligned}$$

(10)

For an imperfect polarizer, an absorption constant should be added. This is omitted from the paper since the factor later cancels out (assuming the constant is independent of $\theta _{\mathrm {pol}}$). Combining (10) with (2) leads to [57]:

$$\begin{aligned} \rho = \frac{I_{\max }-I_{\min }}{I_{\min }+I_{\max }} \end{aligned}$$

(11)

A similar pair of equations for (10) can be found for diffuse reflection by considering the transmission coefficients from the medium to air, as stated in Sect. 3.2.2. This simplifies to (11), just as for specular reflection.

Substituting the relevant Fresnel coefficients into (11) for specular and diffuse cases yields relationships between the viewing angle ($\theta _r$ for specular and $\theta _t'$ for diffuse) and the degree of polarization. The result for the degree of polarization for the specular case, $\rho _s$, and diffuse case, $\rho _d$, is, respectively:

$$\begin{aligned} \rho _s= & {} \frac{2\sin ^2\theta \cos \theta \sqrt{n^2-\sin ^2\theta }}{n^2-\sin ^2\theta -n^2\sin ^2\theta +2\sin ^4\theta } \end{aligned}$$

(12)

$$\begin{aligned} \rho _d= & {} \frac{\left( n-1/n\right) ^2\sin ^2\theta }{2+2n^2-\left( n+1/n\right) ^2\sin ^2\theta +4\cos \theta \sqrt{n^2-\sin ^2\theta }} \nonumber \\ \end{aligned}$$

(13)

These equations are plotted in Fig. 3. Noteworthy features of the relationships include:

• the degree of polarization is significantly larger for specular reflection compared to diffuse reflection except for very large viewing angles.

• there is a small, but significant, dependence of refractive index.

• the degree of polarization increases monotonically for diffuse reflection, but obeys a two-to-one relationship with viewing angle for specular reflection.

Fig. 3

Relationship between degree of polarization and viewing angle for specular and diffuse reflection. Graphs for two demonstrative refractive indices are shown

The key theoretical results are that the phase of polarization is perpendicular to the angle of the plane of reflection for the specular case but equal to the angle of the plane of reflection for the diffuse case, while (12) and (13) relate the degree of polarization to the angle of the surface relative to the viewer. The angle of the plane of reflection is often referred to as the azimuth angle, $\alpha$, while the angle of the surface (normal) relative to the viewer is called the zenith angle, $\theta$. Figure 2 clarifies the relationship between the azimuth angle for a reflecting surface and the phase angle of the light. Technically, there are two possible azimuth angle possibilities for a given phase and reflectance type since the polarizer has no distinction between $\theta _{\mathrm {pol}}$ and $\theta _{\mathrm {pol}}+\,180^{\circ }$ whereas a surface azimuth has the range $[0^{\circ },360^{\circ })$.

4 Polarization image acquisition

This section covers the hardware and data processing necessary for high-quality polarization images to be acquired. Section 4.1 provides basic details of the hardware used. In Sect. 4.2, a basic polarization image of a snooker ball ($50\,\mathrm {mm}$ diameter) is evaluated and compared to expectation. Section 4.3 considers the relative importance of the various aspects of the sensing hardware. In particular, the importance of well-controlled illumination is discussed with examples of the consequences of slight variations. In Sect. 4.4, a variety of methods for data processing are considered to calculate the full polarization images from the raw data. The resulting images are then compared to those found from the POLKA in Sect. 4.5. Key findings are summarized in Sect. 4.6.

Fig. 4

Example polarization image of a white snooker ball with no inter-reflections and only one specularity. a Intensity I, b phase angle $\phi$, c degree of polarization $\rho$

4.1 Capture hardware

Full parametrization of (linear) polarization data require three values, as explained in Sect. 3.1 (either $S_0$, $S_1$ and $S_2$ of the Stokes vector, or I, $\phi$ and $\rho$). Therefore, a minimum of three measurements must be made for each pixel in order to recover a full polarization image. Polarization images are therefore typically acquired by measuring transmission through a polarizing film at three or more different angles. For this paper, the primary focus is the basic method of using a rotating polarizer placed in front of a camera at different orientations. A special camera (POLKA) where each pixel is sensitive to polarized light of a particular phase angle is also briefly considered.

For the former of these, a motor-controlled Hoya CIR-PL circular polarizer was used (which has advantages over a linear polarizer as explained in Sects. 4.3 and [23]). As a baseline, the motor rotates the polarizer to four different angles to determine the Stokes vector although variations of this are investigated. The camera used was a monochrome Dalsa Genie HM1400 fitted with a Schneider KMP-IR Xenoplan 23/1,4-M30,5 lens focused to approximately $550\,\mathrm {mm}$. It was assumed that perspective effects are minimal. Clearly, the noise levels of the camera affect the precision of polarization measurements somewhat. While it was not practical to repeat experiments with a huge number of cameras, some of the experiments were repeated using one particular alternative: a Point Grey Grasshopper GS3-U3-41C6C-C. This showed that there were no major camera-specific trends affecting results.

The lens was of high quality with anti-reflection coatings to minimize internal reflections. It was experimentally determined that the black level of the camera was not zero (specifically $-\,0.03$, where the maximum intensity is 1) by plotting measured pixel brightness against exposure and extrapolating to zero exposure. Therefore, a value of 0.03 was added to all raw intensity measurements captured by the camera before further processing.

The second capture hardware comprises the Fraunhofer “POLKA” camera that was introduced in Sect. 2.1. The POLKA is able to capture all the data simultaneously, while the other method takes at least a few seconds in total while the filter is rotated. This has obvious implications regarding the range of applicability of the two approaches. It is important to note however, that this paper is concerned with high-sensitivity measurements, rather than acquisition time. It is therefore often necessary to take multiple measurements for each scenario in order to minimize noise. This is particularly important for diffuse reflection at low zenith angles since the degree of polarization is very low for such cases (see Fig. 3).

4.2 Baseline analysis

Figure 4 shows the result of capturing a full polarization image of the white snooker ball using the baseline rotating polarizer method described in Sect. 4.1. This was captured using a white LED placed close to the camera and the average of 100 images taken for $\theta _{\mathrm {pol}}=[0^{\circ },45^{\circ },90^{\circ },135^{\circ }]$ (see Sect. 4.4). The capture conditions were such that inter-reflections within the environment were minimized so the only specularity was the direct reflection from the LED (which was saturated). This means that the reflection type is diffuse across the surface.

For the phase image, it is clear that the values are aligned with the azimuth angle, as expected for diffuse reflection (see Fig. 2). The degree of polarization increases near the occluding contours, again as expected (see Fig. 3). The phase image has more noise near the centre since the degree of polarization is very low in that region (and so the four raw images have little intensity variation). The angular error compared to theory for diffuse reflection is shown in Fig. 5a. The mean error is $2.04^{\circ }$ (this error metric will be termed $\overline{\Delta \phi }$ for the remainder of the paper and is calculated such that $\theta \equiv \theta +\,180^{\circ }$). As is apparent from the figure, most of this error is due to the region near the centre of the ball and is largely explained by the low degree of polarization, and hence high noise, in that area. Using the median error ($\widetilde{\Delta \phi }$) gives a value of $0.83^{\circ }$, which can be partly explained by the uncertainty in polarizer angle calibration, which is estimated at $\pm \,0.5^{\circ }$.

Fig. 5

a Angular error in degrees between measured and predicted phase. b Estimated degree of polarization error

To compare the degree of polarization to ground truth, the refractive index must be known, which is not generally the case. For this reason, (13) was used to simulate degree of polarization measurements for a range of refractive index values and that corresponding to minimum variation from the measured data was assumed correct (in this case $n=1.6$). The RMS error between the theoretical calculation and experimental data was then determined as $1.17\%$ (error metric termed $\overline{\Delta \rho }$). On close examination, it was found that this error is dominated by the occluding contours. Using the median error ($\widetilde{\Delta \rho }$) therefore reduces the error significantly; in this case to $0.24\%$.

These error figures mostly are comparable to those published previously for phase but superior for degree of polarization (although very little published data exist for comparison) [1, 7, 50, 59, 60].

4.3 Capture method analysis

This section considers the importance of varying aspects of the capture conditions. Specifically:

• use of circular vs. linear polarizers.

• precision of polarizer positioning.

• use of 8 vs. 10 bits for image storage.

• illumination colour.

• illumination position.

• illumination stability.

Table 1 summarizes the results. Note that the main message here is the relative values since the absolute errors will largely depend on the camera.

The first variation from the baseline was to replace the circular polarizer with a linear one (Hama 00072546). As explained by Karpel and Schechner [23], there are potential advantages of a circular polarizer, which consists of a linearly polarizing film with a quarter-wave plate at the back. The linearly polarizing film ensures that the desired component of the incoming light is transmitted, while the quarter-wave plate converts the transmitted light into a circularly polarized state. Due to the axisymmetric nature of the circularly polarized light, it should not be anisotropically affected by the geometry of the optics of the lens or camera. As shown in Table 1, the quality of results is indeed inferior where a linear polarizer is used instead of a circularly polarizing filter.

Table 1 Summary of numerical error analysis for various hardware and capture conditions

Fig. 6

Phase and degree of polarization errors for varying error in polarizer angle error ($\Delta \theta _{\mathrm {pol}}$)

The next aspect of capture hardware to be considered was the positioning of the polarizer. Figure 6 shows the phase and degree of polarization errors where the polarizer angle, $\theta _{\mathrm {pol}}$, has fixed errors induced. The polarizer angle error, $\Delta \theta _{\mathrm {pol}}$, is defined such that a value of $n^{\circ }$ increases the angular separation between image captures by $(45+n)^{\circ }$ rather than $45^{\circ }$. Not surprisingly, the phase error is shown to increase in proportion to $\Delta \theta _{\mathrm {pol}}$. The degree of polarization measurements are shown to be highly robust to polarizer angle error. It should be noted that the slope of the lines for the degree of polarization errors increases as the $\Delta \theta _{\mathrm {pol}}$ approaches approximately $10^{\circ }$, but this level of angular error is unlikely to manifest in any real-world applications.

For practical reasons, it is more difficult to reliably induce errors in the polarizer orientation with respect to the image plane. However, a preliminary study whereby the orientation of the polarizer is disrupted (such that it “wobbles” when rotating) revealed that only minor errors are induced when said orientation varies by less than a degree or so.

In order to minimize quantization error, the camera was set to record 10-bit images throughout most of this work. The noise levels in the camera (standard deviation of the order 0.005 for typical conditions, where the maximum possible intensity is 1) would not justify this if only a single image were to be captured for each case. However, the use of multiple images (especially of the order 100 images) justifies the use of more bits. Nevertheless, as shown in the third result of the table, the additional bits were found to offer only very minor improvement.

The light source adopted for this paper was an Engin LZC-03MD07 LED cluster rated at $40\,\mathrm {W}$ capable of emitting white, red ($\lambda \approx 624\,\mathrm {nm}$), green ($\lambda \approx 525\,\mathrm {nm}$) or blue ($\lambda \approx 457\,\mathrm {nm}$) light. The LED was attached to a large heat sink and left to reach a steady temperature before usage. For this experiment, the exposure time of the camera was adjusted to give similar pixel brightnesses for each colour (white: $2.7\,\mathrm {ms}$, red: $2.5\,\mathrm {ms}$, green: $6\,\mathrm {ms}$, blue: $4\,\mathrm {ms}$).

Results for the various colour values in Table 1 demonstrate comparable but unequal performance between the different wavelengths. Since there appeared to be no systematic error present in the results, the differences are likely to be largely due to the wavelength sensitivity profile of the camera as much as any physical phenomenon. That said, it is well known that non-visible wavelengths have varying penetrative properties and thus may result in different outputs. Studies on non-visible light, however, are reserved for future work.

The next results in Table 1 relate to moving the light source from as close to the camera as possible (subtending an angle of $5^{\circ }$ in practice from the optical axis of the camera) to a wide-angle position at $25^{\circ }$. Results are comparable but inferior to the baseline, but with the difference mostly related to shadows rather than more inherent physical phenomena.

One of the most critical aspects of data acquisition is light source stability. Figure 7 shows phase and degree of polarization images for data captured with the electric current through the LED increased (from $600\,\mathrm {mA}$) between each polarizer orientation. Errors for a range of induced current variations are illustrated by the graphs in Fig. 8. The magnitudes of the lower current variations in the graph are typical of LEDs that have only just been illuminated or are in conditions of varying temperature, demonstrating the criticality of a stable light source. Note that these errors are mostly much higher than those given in Table 1. To further emphasize the importance of well-controlled LED current/temperature, it was demonstrated during this research that a person blowing intensely on the LED for half of the image capture can be enough to make polarization images notably different to the unaided eye.

Fig. 7

Phase (top) and degree of polarization images for varying degrees of light source stability. Percentage current variation between each polarizer angle is shown at the top. Degree of polarization values above 0.06 are capped in the image for clarity

Fig. 8

Phase and degree of polarization errors for varying degrees of light source stability

4.4 Polarization image computation

In this section, two methods for calculating the polarization image from the raw data are considered. The first involves taking images at only three or four polarizer angles and using a closed-form calculation of the polarization data. The second method involves capturing images at many different polarizer angles and fitting (9) to the intensities at each pixel.

Fig. 9

Phase and degree of polarization errors for varying number of images per polarizer angle

4.4.1 Closed-form solution

Given that there are three degrees of freedom to a polarization image (I, $\phi$ and $\rho$), a minimum of three images are needed in order to use a closed-form calculation of each. First, the method of Wolff [56] is applied for a three-image closed-form solution, which requires images corresponding to $\theta _{\mathrm {pol}}=[0^{\circ },45^{\circ },90^{\circ }]$:

$$\begin{aligned} \phi= & {} \frac{1}{2}\arctan \left( \frac{I_0+I_{90}-2I_{45}}{I_{90}-I_0} \right) + 90^{\circ } \nonumber \\&\quad \text{ if }\left( I_{90}<I_0\right) \left[ \text{ if }\left( I_{45}<I_0 \right) \phi \leftarrow \phi +90^{\circ } \,\text{ else }\, \phi \leftarrow \phi -90^{\circ } \right] \nonumber \\ \end{aligned}$$

(14)

$$\begin{aligned} I= & {} I_0+I_{90} \end{aligned}$$

(15)

$$\begin{aligned} \rho= & {} \frac{I_{90}-I_0}{\left( I_{90}+I_0\right) \cos 2\phi } \end{aligned}$$

(16)

An alternative closed-form solution is to mimic the POLKA (and some other polarization cameras) and capture a total of four images where $\theta _{\mathrm {pol}}=[0^{\circ },45^{\circ },90^{\circ },135^{\circ }]$ [24]. This method obviously requires more capture time but may result is less directionally biased results given the more even spread of polarizer angles. For this case, the Stokes vector parameters are calculated using the equations below before I, $\phi$ and $\rho$ are determined using (3–5).

$$\begin{aligned} S_0= & {} \frac{I_0 + I_{45} + I_{90} + I_{135}}{2} \end{aligned}$$

(17)

$$\begin{aligned} S_1= & {} I_{0} - I_{90} \end{aligned}$$

(18)

$$\begin{aligned} S_2= & {} I_{45} - I_{135} \end{aligned}$$

(19)

As shown in the bottom line of Table 1, the use of four sources seemingly offers little advantage over the three-source method. However, notable advantages were experimentally found to manifest when only few images were captured per polarizer angle.

Figure 9 shows the precision of the four-angle baseline method using the average of varying numbers of raw images per polarizer angle. This clearly shows that a significant number of images are required to obtain reliable data. It is worth noting, however, that modern cameras can easily capture and average over 100 images in less than a second so the main weakness of the rotating polarizer approach remains the need to capture with multiple orientations: capturing 100 images for each angle is not significantly more difficult than capturing one image for each angle.

4.4.2 Statistical approach

This method involves taking images of the target with the polarizer rotated to a range of different angles. For this paper, between four and 400 angles were used as this matches the total number of images used in Sect. 4.4.1 (the angular resolution of the motor controller prevented the use of more than about 400 images in total). Due to the finite resolution of the motor, the angles were chosen to be spread over $360^{\circ }$, even though the polarizer has no distinction between to angles separated by $180^{\circ }$.

Brightness data for each pixel location were statistically fitted to the TRS (9) using the trust-region-reflective algorithm [10]. From the resulting best fit parameters, the phase was extracted directly while the degree of polarization was determined using the amplitude and offset of the TRS with (11).

An alternative approach, used by Tokuda et al. [50], involved estimating the phase angle directly using many polarizer angles based on a Fourier transform approach:

$$\begin{aligned} \phi = \frac{1}{2}\arctan _2\left( \sum _{\theta _{\mathrm {pol}}=0}^{\theta _{\mathrm {pol}}=179} I_{\mathrm {pol}}\sin \left( 2\theta _{\mathrm {pol}}\right) ,\sum _{\theta _{\mathrm {pol}}=0}^{\theta _{\mathrm {pol}}=179} I_{\mathrm {pol}}\cos \left( 2\theta _{\mathrm {pol}}\right) \right) \end{aligned}$$

(20)

where filter angles between 0 and 179 were used in $1^{\circ }$ increments. This was shown to give exceptionally precise phase estimates (as small as $0.04^{\circ }$ in certain situations with their custom hardware). However, results were variable and the degree of polarization was not computed. For these reasons, and for the sake of compactness, a detailed analysis is not conducted here. However, a brief study showed results comparable to the statistical approach of this paper but with less computation time and poorer results for regions of low degree of polarization.

Results for this statistical approach are shown in Fig. 10 in the same manner as for the closed-form solution results in Fig. 9. As expected, the results are generally of comparable quality, especially where larger numbers of images were used. It was found that results for the closed-form solution are slightly better for small numbers of images, which is due multiple optima existing for the trust-region-reflective algorithm with only few data points.

Fig. 10

Phase and degree of polarization errors using the statistical approach and varying number of polarizer angles

4.5 Comparison to POLKA

As stated in Sect. 2.1, there are several commercially available cameras able to rapidly acquire phase and degree of polarization data. This section compares one such camera to the results using the rotating polarizer method. Specifically, the POLKA [16] is used. Capture conditions and the test object are identical to previous experiments except that the light source was replaced by an $850\,\mathrm {nm}$ LED as the POLKA is designed for near-infrared illumination. This does, of course, mean that a comparison between methods is limited in some regard. The results below should therefore be interpreted only loosely. Furthermore, it is worth remembering that the POLKA has the ability to obtain a polarization image with a single raw image capture and hence has applications to non-static scenes, which the rotating polarizer method does not.

Table 2 summarizes the results to compare the two capture methods. The first row shows results using a single image from the POLKA, while the second takes the mean over 100 frames. Results using the rotating polarizer approach with one image and 100 images per polarizer angle are also included. This shows that the level of precision is notably superior for the rotating polarizer. One may argue that a fairer test would be to compare the results using 100 images from the POLKA to 25 images per polarizer angle, since the latter requires a total of 100 images. Nevertheless, results are still superior using the rotating polarizer approach, albeit by a smaller margin.

Table 2 Comparison between the baseline rotating polarizer method with that of the POLKA for various numbers of images

4.6 Summary

The results so far demonstrate that for most non-moving applications, the following are the most significant parameters for optimal data capture:

• circular polarizer rather than linear polarizer.

• images taken at four polarizer angles using the closed-form solution.

• white or green LED with very steady current.

• up to 100 images may be necessary for each polarizer angle to obtain relatively noise-free results for a typical mid-priced machine vision camera. Little improvement is likely beyond 100 images.

Note that the last two points will vary with the noise properties of the camera used to some degree. A more detailed summary of the various research questions is shown in Table 3.

Table 3 Summary of key research questions, relative importance and outcomes

Fig. 11

a Intensity, b phase and c degree of polarization of a white porcelain cup showing an inter-reflection from the handle. The degree of polarization is cropped at 0.1 here to enhance the appearance of the inter-reflection

5 Observable phenomena

The previous section aimed to optimize the data capture and processing approach using the simple case of diffuse-dominated reflection from a smooth white surface. In this section, the optimum approach summarized in Sect. 4.6 is used to investigate a range of other reflection polarization phenomena found in everyday environments. The main phenomena considered are specularities present in images and the effect of surface colour and roughness.

5.1 Specularities and inter-reflections

Figure 11 shows the polarization image of a smooth white porcelain cup. As with results for the white snooker ball, the phase and degree of polarization data broadly match expectation for diffuse reflection. However, close examination of the cup near the handle reveals different behaviour: an inter-reflection from the handle to the body of the cup. While this is only just visible in the intensity image, it is very clear in the phase and degree of polarization images. For the phase, there is a $90^{\circ }$ phase shift around the edge of the inter-reflection, indicating that specular reflection theory (Sect. 3.2.1) is dominating over diffuse reflection theory (Sect. 3.2.2). However, the degree of polarization for this area is low since the two reflection types are “in competition.”

To investigate this further, consider Fig. 12 which shows white snooker ball polarization images with a white acrylic board placed behind. The figure shows images with the board $200\,\mathrm {mm}$ behind the ball (a–c) and immediately behind the ball (d–f). Note that the noise-ridden background to Fig. 12 is due to the very low degree of polarization on the board and the shadow cast by the ball; neither of which are significant to the paper. Both cases in Fig. 12 demonstrate a specular inter-reflection from the board forming a region of $90^{\circ }$ phase shift around the outer perimeter of the ball. The closer the board is to the ball, the larger the area of specular-dominated inter-reflection. As with the inter-reflection on the cup in Fig. 11, the degree of polarization is reduced where the diffuse/specular effects are competing.

Fig. 12

a Intensity, b phase and c degree of polarization of a white snooker ball with a white acrylic board placed $200\,\mathrm {mm}$ behind the centre of the ball. d–f Board placed immediately behind the ball

The size of the specular region for inter-reflections depends on various parameters of the capture conditions. Of particular interest is the colour of the ball. Figure 13 shows similar results to Fig. 12 including a red, blue and black ball. The exposure time for these was adjusted to maximize the dynamic range of intensities in the raw images (white: $3\,\mathrm {ms}$, red: $6\,\mathrm {ms}$, blue: $14\,\mathrm {ms}$, black: $15.5\,\mathrm {ms}$), but all other parameters were identical for each ball. The balls in Fig. 13 are ordered from lightest to darkest.

Fig. 13

a Intensity, b phase and c degree of polarization of a white snooker ball with a white acrylic board placed immediately behind the ball. d–f Red ball. g–i Blue ball. j–l Black ball. N.B. The small patch of phase change just below the centre of the ball is a reflection from the ground

Careful examination of the intensity images in Fig. 13 reveals the region of the ball where the specular inter-reflection is present. This is most apparent for darker balls since those have a much smaller diffuse component due to greater absorption of light. This phenomenon also explains why the region of phase shifts is also larger for darker balls. Finally, note that the degree of polarization is larger for darker balls since the diffuse component becomes negligible for dark balls (the scale on the degree of polarization images in Fig. 13 is different to that of earlier figures). Indeed, the degree of polarization was found to be greater than 0.9 in places for the black ball indicating near-perfect specular reflection.

5.2 Other phenomena

The theory described in Sect. 3 applies to smooth dielectric surfaces. As a brief illustration of a rough surface, consider Fig. 14 which shows the polarization image of a white snooker ball that has been sandblasted to roughen its surface somewhat. The primary difference to the smooth ball shown in Figs. 4 and 12 is that the degree of polarization is reduced due to microscopic inter-reflections between surface “microfacets” [33, 51, 58] randomizing the phase angle. Since each pixel in the images would correspond to many microfacets, the degree of polarization will be “macroscopically depolarized.” Due to the lower degree of polarization for rough surfaces, the noise levels of the data are higher in such cases, as is illustrated by comparing the centre of the phase images in Figs. 4 and 14. Note that the inter-reflection is still visible near the occluding contours when the board is placed behind the ball.

The inferences about Fig. 14 are supported by the various error metrics. The phase error values for the sandblasted ball image are $\overline{\Delta \phi } = 2.58^{\circ }$ and $\widetilde{\Delta \phi } = 1.05^{\circ }$ while the degree of polarization error values are $\overline{\Delta \rho } = 2.58\%$ and $\widetilde{\Delta \rho } = 1.75\%$. Note that the increase in phase error compared to the baseline in Table 1 is smaller than that of the degree of polarization. This is due to the fact that phase accuracy is only affected by the higher noise levels (a random error) while degree of polarization is affected by both higher noise and depolarization (systematic error).

Fig. 14

a Intensity, b phase and c degree of polarization of a sandblasted white snooker ball. d–f Same ball with white board immediately behind

Figure 15 shows the polarization image of a slightly rough plastic novelty ball. This is to demonstrate that neither the phase nor degree of polarization is majorly affected by variations in the albedo of the surface (the patterns are barely visible in Fig. 15b, c). This may have future implications of shape analysis where surface orientation may be estimated irrespective of albedo.

Fig. 15

a Intensity, b phase and c degree of polarization of a novelty ball

Finally, Fig. 16 shows the polarization image of a slightly rough plastic mask. This demonstrates a range of the phenomena observed in this paper in a single image including: mostly diffuse behaviour; reduced degree of polarization due to roughness; and specular inter-reflections (perhaps most visible to the left side of the of nose). Note that the data are relatively unaffected by the albedo changes around the eyes and nose.

Fig. 16

a Intensity, b phase and c degree of polarization of plastic mask

6 Conclusion

This paper has presented the state of the art in the field of polarization vision, a detailed analysis of all notable acquisition parameters and a thorough comparison between captured results and theoretical expectation. The results from Sect. 4 are of significance to future research aimed at using polarization imaging as they indicate optimal conditions and processes for data acquisition. Sections 4 and 5 collectively demonstrate that current reflectance theories (Fresnel and Wolff) accurately model the polarizing properties of reflection for cases with and without specular-dominated inter-reflections. The presented results also highlight some of the features that need to be considered in future applications of polarization vision such as robotic navigation or scene understanding.

In future work, it is hoped that similar data capture and processing methods will be studied for conditions involving polarization by scattering in haze or underwater. Furthermore, a more detailed study of reflection where both diffuse and specular components are present but with neither type being negligible is desired (such as the area of low degree of polarization near the handle of the cup in Fig. 11). This would open applications to less controlled capture environments. Other potentially useful areas of future work include extending the analysis to non-visible light and metallic surfaces, and parametrizing roughness for full quantitative analysis of the effects of surface texture.