Abstract
Key message
For genomewide selection in each biparental population, it is better to use a smaller ad hoc training population than a single, large training population.
Abstract
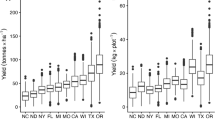
In genomewide selection, different types of training populations can be used for a biparental population made from homozygous parents (A and B). Our objective was to determine whether the response to selection (R) and predictive ability (rMP) in an A/B population are higher with a large training population that is used for all biparental crosses, or with a smaller ad hoc training population highly related to the A/B population. We studied 969 biparental maize (Zea mays L.) populations phenotyped at four to 12 environments. Parent–offspring marker imputation was done for 2911 single nucleotide polymorphism loci. For 27 A/B populations, training populations were constructed by pooling: (1) all prior populations with A as one parent (A/*, where * is a related inbred) and with B as one parent (*/B) [general combining ability (GCA) model]; (2) A/* or */B crosses only; (3) all */* crosses (same background model, SB); and (4) all */*, A/*, and */B crosses (SB + GCA model). The SB model training population was 450–6000% as large as the GCA model training populations, but the mean coefficient of coancestry between the training population and A/B population was lower for the SB model (0.44) than for the GCA model (0.71). The GCA model had the highest R and rMP for all traits. For yield, R was 0.22 Mg ha−1 with the GCA model and 0.15 Mg ha−1 with the SB model. We concluded that it is best to use an ad hoc training population for each A/B population.

Similar content being viewed by others
References
Bernardo R (1993) Estimation of coefficient of coancestry using molecular markers in maize. Theor Appl Genet 85:1055–1062
Bernardo R (2010) Breeding for quantitative traits in plants, 2nd edn. Stemma Press, Woodbury. ISBN 978-0-9720724-1-0
Brandariz SP, Bernardo R (2018) Maintaining the accuracy of genomewide predictions when selection has occurred in the training population. Crop Sci 58:1–6
Combs E, Bernardo R (2013) Accuracy of genomewide selection for different traits with constant population size, heritability, and number of markers. Plant Genome. https://doi.org/10.3835/plantgenome2012.11.0030
Daetwyler HD, Villanueva B, Woolliams JA (2008) Accuracy of predicting the genetic risk of disease using a genome-wide approach. PLoS ONE 3:e3395
Daetwyler HD, Pong-Wong R, Villanueva B, Woolliams JA (2010) The impact of genetic architecture on genome-wide evaluation methods. Genetics 1031:1021–1031
Endelman JB (2011) Ridge regression and other kernels for genomic selection with R package rrBLUP. Plant Genome 4:250–255
Endelman JB, Atlin GN, Beyene Y, Semagn K, Zhang X, Sorrells ME, Jannink J (2014) Optimal design of preliminary yield trials with genome-wide markers. Crop Sci 54:48–59
Heffner EL, Jannink JL, Sorrells ME (2011) Genomic selection accuracy using multifamily prediction models in a wheat breeding program. Plant Genome 4:1–11
Heslot N, Yang HP, Sorrells ME, Jannink JL (2012) Genomic selection in plant breeding: a comparison of models. Crop Sci 52:146–160
Hickey JM, Dreisigacker S, Crossa J, Hearne S, Babu R, Prasanna BM, Grondona M, Zambelli A, Windhausen VS, Mathews K, Gorjanc G (2014) Evaluation of genomic selection training population designs and genotyping strategies in plant breeding programs using simulation. Crop Sci 54:1476–1488
Jacobson A, Lian L, Zhong S, Bernardo R (2014) General combining ability model for genomewide selection in a biparental cross. Crop Sci 54:895–905
Jacobson A, Lian L, Zhong S, Bernardo R (2015a) Marker imputation before genomewide selection in biparental maize populations. Plant Genome 8:1–9
Jacobson A, Lian L, Zhong S, Bernardo R (2015b) Minimal loss of genetic diversity after genomewide selection within biparental maize populations. Crop Sci 55:783–789
Lian L, Jacobson A, Zhong S, Bernardo R (2014) Genomewide prediction accuracy within 969 maize biparental populations. Crop Sci 54:1514–1522
Lorenz AJ, Smith KP (2015) Adding genetically distant individuals to training populations reduces genomic prediction accuracy in barley. Crop Sci 55:2657–2667
Lorenzana RE, Bernardo R (2009) Accuracy of genotypic value predictions for marker-based selection in biparental plant populations. Theor Appl Genet 120:151–161
Lynch M (1988) Estimation of relatedness by DNA fingerprinting. Mol Biol Evol 5:584–599
Parra JR, Hallauer AR (1996) Utilization of exotic maize germplasm. In: Janick J (ed) Plant breeding reviews, vol 14. Wiley, Oxford, pp 165–187
Phillips RL (2010) Mobilizing science to break yield barriers. Crop Sci 50:S-99–S-108
Riedelsheimer C, Technow F, Melchinger AE (2012) Comparison of whole-genome prediction models for traits with contrasting genetic architecture in a diversity panel of maize inbred lines. BMC Genom 13:452
Riedelsheimer C, Endelman JB, Stange M, Sorrells ME, Jannink J-L, Melchinger AE (2013) Genomic predictability of interconnected biparental maize populations. Genetics 194:493–503
Schulz-Streeck T, Ogutu JO, Karaman Z, Knaak C, Piepho HP (2012) Genomic selection using multiple populations. Crop Sci 52:2453–2461
Sokal RR, Michener CD (1958) A statistical method for evaluating systematic relationships. Univ Kansas Sci Bull 38:1409–1438
R Core Team (2017) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/
Acknowledgements
Sofía P. Brandariz was supported by Ph.D. fellowship funded by Monsanto. We thank Drs. David Butruille, Mike Lohuis, and Sam Eathington for allowing us to use the data sets in this study, and Dr. Shengqiang Zhong for his valuable input and insights on our work with these data sets since 2011.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by Hiroyoshi Iwata.
Rights and permissions
About this article
Cite this article
Brandariz, S.P., Bernardo, R. Small ad hoc versus large general training populations for genomewide selection in maize biparental crosses. Theor Appl Genet 132, 347–353 (2019). https://doi.org/10.1007/s00122-018-3222-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00122-018-3222-3