Skip to main content
SpringerLink
Log in

Global Exponential Stability Conditions for Discrete-Time BAM Neural Networks Affected by Impulses and Time-Varying Delays

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

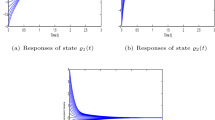
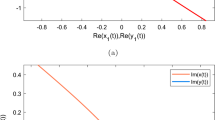
This paper studies global exponential stability (GES) of discrete-time (D-T) BAM neural networks (BAMNNs) affected by impulses and time-varying delays. An impulse-free D-T BAMNN with time-varying delays is first developed via the properties of M-matrices, and then the relation between the solutions of the original and new BAMNNs is established. From which, sufficient conditions for GES of the original BAMNN are derived by investigating GES conditions of the new BAMNN based on the counter-evidence and the nature of the nonsingular M-matrix. The results of illustrative examples show that the obtained GES criteria are effective. By comparing with previous results, this paper has the following three merits: (a) the obtained GES criteria are to check the positivity of eigenvalues of a constant matrix, which is easy to realize; (b) this method can be used for other D-T system models affected by impulses and time-varying delays; and (c) the numerical results show that our method is less conservative than ones in other literatures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data Availability

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

References

  1. M. Baleya, H. Shalaby, K. Kato, M. Elsabrouty, Neural network ensemble for precise laser spot position determination on a quadrant detector. IEEE Photonics Technol. Lett. 36(2), 115–118 (2024)

    Article  Google Scholar 

  2. J. Cheng, L. Liang, H. Yan, J. Cao, S. Tang, K. Shi, Proportional-integral observer-based state estimation for Markov memristive neural networks with sensor saturations. IEEE Trans. Neural Netw. Learn. Syst. 35(1), 405–416 (2024)

    Article  MathSciNet  Google Scholar 

  3. J. Cheng, J.H. Park, Z.-G. Wu, Finite-time control of Markov jump Lur’e systems with singular perturbations. IEEE Trans. Autom. Control 68(11), 6804–6811 (2023)

    Article  MathSciNet  Google Scholar 

  4. E.-Y. Cong, X. Han, X. Zhang, Global exponential stability analysis of discrete-time BAM neural networks with delays: a mathematical induction approach. Neurocomputing 379, 227–235 (2020)

    Article  Google Scholar 

  5. Z. Dong, X. Wang, X. Zhang, A nonsingular M-matrix-based global exponential stability analysis of higher-order delayed discrete-time Cohen–Grossberg neural networks. Appl. Math. Comput. 385, 125401 (2020)

    MathSciNet  Google Scholar 

  6. Z. Dong, X. Wang, X. Zhang, M. Hu, T.N. Dinh, Global exponential synchronization of discrete-time high-order switched neural networks and its application to multi-channel audio encryption. Nonlinear Anal. Hybrid Syst. 47, 101291 (2023)

    Article  MathSciNet  Google Scholar 

  7. Z. Dong, X. Zhang, X. Wang, Global exponential stability of discrete-time higher-order Cohen-Grossberg neural networks with time-varying delays, connection weights and impulses. J. Franklin Inst. 358(11), 5931–5950 (2021)

    Article  MathSciNet  Google Scholar 

  8. B. Kosko, Adaptive bidirectional associative memories. Appl. Opt. 26(23), 4947–4960 (1987)

    Article  Google Scholar 

  9. X. Li, F. Li, X. Zhang, C. Yang, W. Gui, Exponential stability analysis for delayed semi-Markovian recurrent neural networks: a homogeneous polynomial approach. IEEE Trans. Neural Networks Learn. Syst. 29(12), 6374–6384 (2018)

    Article  MathSciNet  Google Scholar 

  10. J. Li, Q. Zhu, Stability of neutral stochastic delayed systems with switching and distributed-delay dependent impulses. Nonlinear Anal. Hybrid Syst. 47, 101279 (2023)

    Article  MathSciNet  Google Scholar 

  11. J. Liang, J. Cao, D.W. Ho, Discrete-time bidirectional associative memory neural networks with variable delays. Phys. Lett. A 335(2–3), 226–234 (2005)

    Article  Google Scholar 

  12. X.-G. Liu, M.-L. Tang, R. Martin, X.-B. Liu, Discrete-time BAM neural networks with variable delays. Phys. Lett. A 367(4–5), 322–330 (2007)

    Article  Google Scholar 

  13. R.J. Plemmons, M-matrix characterizations. I-nonsingular M-matrices. Linear Algebra Appl. 18(2), 175–188 (1977)

    Article  MathSciNet  Google Scholar 

  14. G. Rajchakit, P. Chanthorn, M. Niezabitowski, R. Raja, D. Baleanu, A. Pratap, Impulsive effects on stability and passivity analysis of memristor-based fractional-order competitive neural networks. Neurocomputing 417, 290–301 (2020)

    Article  Google Scholar 

  15. G. Rajchakit, R. Sriraman, C.P. Lim, B. Unyong, Existence, uniqueness and global stability of Clifford-valued neutral-type neural networks with time delays. Math. Comput. Simul. 201, 508–527 (2022)

    Article  MathSciNet  Google Scholar 

  16. G. Rajchakit, R. Sriraman, Robust passivity and stability analysis of uncertain complex-valued impulsive neural networks with time-varying delays. Neural Process. Lett. 53(1), 581–606 (2021)

    Article  Google Scholar 

  17. G. Rajchakit, R. Sriraman, P. Vignesh, C.P. Lim, Impulsive effects on Clifford-valued neural networks with time-varying delays: an asymptotic stability analysis. Appl. Math. Comput. 407, 126309 (2021)

    MathSciNet  Google Scholar 

  18. H. Shen, Z. Huang, Z. Wu, J. Cao, J.H. Park, Nonfragile \({H}_{\infty }\) synchronization of BAM inertial neural networks subject to persistent dwell-time switching regularity. IEEE Trans. Cybernet. 52(7), 6591–6602 (2022)

    Article  Google Scholar 

  19. Y. Sheng, T. Huang, Z. Zeng, P. Li, Exponential stabilization of inertial memristive neural networks with multiple time delays. IEEE Trans. Cybernet. 51(2), 579–588 (2021)

    Article  Google Scholar 

  20. Y. Sheng, Z. Zeng, T. Huang, Finite-time stabilization of competitive neural networks with time-varying delays. IEEE Trans. Cybernet. 52(11), 11325–11334 (2022)

    Article  Google Scholar 

  21. X. Song, X. Sun, J. Man, S. Song, Q. Wu, Synchronization of fractional-order spatiotemporal complex-valued neural networks in finite-time interval and its application. J. Franklin Inst. 358(16), 8207–8225 (2021)

    Article  MathSciNet  Google Scholar 

  22. C. Sowmiya, R. Raja, J. Cao, X. Li, G. Rajchakit, Discrete-time stochastic impulsive BAM neural networks with leakage and mixed time delays: an exponential stability problem. J. Franklin Inst. 355(10), 4404–4435 (2018)

    Article  MathSciNet  Google Scholar 

  23. C. Sowmiya, R. Raja, J. Cao, G. Rajchakit, A. Alsaedi, A delay-dependent asymptotic stability criteria for uncertain BAM neural networks with leakage and discrete time-varying delays: A novel summation inequality. Asian J. Control 22(5), 1880–1891 (2020)

    Article  MathSciNet  Google Scholar 

  24. C. Sowmiya, R. Raja, J. Cao, G. Ravi, X. Li, A. Alsaedi, Z. Tu, Global exponential stability of antiperiodic solutions for impulsive discrete-time Markovian jumping stochastic BAM neural networks with additive time-varying delays and leakage delay. Int. J. Adapt. Control Signal Process. 32(6), 908–936 (2018)

    Article  MathSciNet  Google Scholar 

  25. C. Sowmiya, R. Raja, Q. Zhu, G. Rajchakit, Further mean-square asymptotic stability of impulsive discrete-time stochastic BAM neural networks with Markovian jumping and multiple time-varying delays. J. Franklin Inst. 356(1), 561–591 (2019)

    Article  MathSciNet  Google Scholar 

  26. Y. Shu, X. Liu, F. Wang, S. Qiu, Further results on exponential stability of discrete-time BAM neural networks with time-varying delays. Math. Methods Appl. Sci. 40(11), 4014–4027 (2017)

    Article  MathSciNet  Google Scholar 

  27. G. Sun, Y. Zhang, Exponential stability of impulsive discrete-time stochastic BAM neural networks with time-varying delay. Neurocomputing 131, 323–330 (2014)

    Article  Google Scholar 

  28. S.K. Thangarajan, A. Chokkalingam, Integration of optimized neural network and convolutional neural network for automated brain tumor detection. Sens. Rev. 41(1), 16–34 (2021)

    Article  Google Scholar 

  29. N.M. Thoiyab, P. Muruganantham, Q. Zhu, N. Gunasekaran, Novel results on global stability analysis for multiple time-delayed BAM neural networks under parameter uncertainties. Chaos Solitons Fractals 152, 111441 (2021)

    Article  MathSciNet  Google Scholar 

  30. X. Wang, J.H. Park, H. Liu, X. Zhang, Cooperative output-feedback secure control of distributed linear cyber-physical systems resist intermittent DoS attacks. IEEE Trans. Cybernet. 51(10), 4924–4933 (2021)

    Article  Google Scholar 

  31. X. Wang, J.H. Park, H. Yang, S. Zhong, A new settling-time estimation protocol to finite-time synchronization of impulsive memristor-based neural networks. IEEE Trans. Cybernet. 52(6), 4312–4322 (2022)

    Article  Google Scholar 

  32. J. Wang, X. Wang, X. Zhang, S. Zhu, Global \(h\)-synchronization of high-order delayed inertial neural networks via direct SORS approach. IEEE Trans. Syst. Man Cybernet. Syst. 53(11), 6693–6704 (2023)

    Article  Google Scholar 

  33. X. Wang, G.H. Yang, Fault-tolerant consensus tracking control for linear multiagent systems under switching directed network. IEEE Trans. Cybernet. 50(5), 1921–1930 (2020)

    Article  Google Scholar 

  34. H. Xiao, X. Hu, T. Gao, Y. Zhou, S. Duan, Y. Chen, Efficient low-bit neural network with memristor-based reconfigurable circuits. IEEE Trans. Circuits Syst. II Express Briefs 71(1), 66–70 (2024)

    Google Scholar 

  35. J. Xiao, S. Wen, X. Yang, S. Zhong, New approach to global Mittag–Leffler synchronization problem of fractional-order quaternion-valued BAM neural networks based on a new inequality. Neural Netw. 122, 320–337 (2020)

    Article  Google Scholar 

  36. L. Xing, L. Zhou, Polynomial dissipativity of proportional delayed BAM neural networks. Int. J. Biomath. 13(6), 2050050 (2020)

    Article  MathSciNet  Google Scholar 

  37. Y. Xue, C. Liu, X. Zhang, State bounding description and reachable set estimation for discrete-time genetic regulatory networks with time-varying delays and bounded disturbances. IEEE Trans. Syst. Man Cybernet. Syst. 52(10), 6652–6661 (2022)

    Article  Google Scholar 

  38. X. Zhang, X. Fan, L. Wu, Reduced- and full-order observers for delayed genetic regulatory networks. IEEE Trans. Cybernet. 48(7), 1989–2000 (2018)

    Article  Google Scholar 

  39. X. Zhang, Y. Han, L. Wu, Y. Wang, State estimation for delayed genetic regulatory networks with reaction–diffusion terms. IEEE Trans. Neural Netw. Learn. Syst. 29(2), 299–309 (2018)

    Article  MathSciNet  Google Scholar 

  40. L. Zhang, Y. Yang, Finite time impulsive synchronization of fractional order memristive BAM neural networks. Neurocomputing 384, 213–224 (2020)

    Article  Google Scholar 

  41. Y. Zhang, L. Zhou, Novel global polynomial stability criteria of impulsive complex-valued neural networks with multi-proportional delays. Neural Comput. Appl. 34(4), 2913–2924 (2022)

    Article  MathSciNet  Google Scholar 

  42. Y. Zhang, L. Zhou, Stabilization and lag synchronization of proportional delayed impulsive complex-valued inertial neural networks. Neurocomputing 507, 428–440 (2022)

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the Natural Science Foundation of Heilongjiang Province, China (YQ2021F014), the Basic Research Foundation for Outstanding Young Teachers in Heilongjiang Provincial Universities of China (Grant No. YQJH2023141), and the Fundamental Research Funds in Heilongjiang Provincial Universities of China (2022-KYYWF-1099). The authors would like to thank the anonymous associate editor and reviewers for their helpful comments and suggestions, which greatly improves the original version of the paper.

Author information

Authors and Affiliations

  1. School of Mathematical Science, Heilongjiang University, Harbin, 150080, China

    Wanning Li, Xian Zhang & Xiaona Yang

  2. Heilongjiang Provincial Key Laboratory of the Theory and Computation of Complex Systems, Heilongjiang University, Harbin, 150080, China

    Wanning Li, Xian Zhang & Xiaona Yang

  3. School of Information Management, Heilongjiang University, Harbin, 150080, China

    Chunyan Liu

Authors
  1. Wanning Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xian Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chunyan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiaona Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Chunyan Liu or Xiaona Yang.

Ethics declarations

Conflict of interest

The authors have no conflict of interest to declare.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, W., Zhang, X., Liu, C. et al. Global Exponential Stability Conditions for Discrete-Time BAM Neural Networks Affected by Impulses and Time-Varying Delays. Circuits Syst Signal Process (2024). https://doi.org/10.1007/s00034-024-02701-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00034-024-02701-6

Keywords

Search

Navigation