Widely Linear Complex-Valued Least Mean M-Estimate Algorithms: Design and Performance Analysis

Abstract

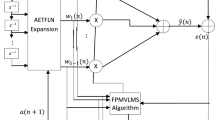
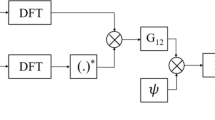
To utilize the full second-order statistical information of the complex-valued signal, a widely linear complex-valued LMM (WL-CLMM) algorithm is proposed by using different M-estimate functions. The proposed WL-CLMM algorithm can process both circular and noncircular complex-valued signals in impulsive noise environments. Moreover, a novel adaptive threshold adjustment method for the M-estimate function is designed according to the probability density function of the complex-valued error signal. In addition, to decrease the sensitivity of the input signal to the performance of the algorithm, the normalized version of WL-CLMM (WL-CNLMM) has been developed. Then, we carry out the mean behavior and mean square behavior analysis of the proposed algorithms. Simulation results show that the proposed algorithms outperform some existing complex-valued algorithms and the theoretical results are well matched.

Appendix

In this Appendix, Wirtinger calculus is briefly described. Wirtinger calculus provides a framework for differentiating nonanalytic functions and it allows performing all the derivations in the complex domain, in a manner very similar to the real-valued case. For a complex-valued function $f(z)$, where $z = z_{r} + jz_{i}$, two generalized complex derivatives can be defined as

$$ \frac{\partial f}{{\partial z}} \triangleq \frac{1}{2}\left( {\frac{\partial f}{{\partial z_{r} }} - j\frac{\partial f}{{\partial z_{i} }}} \right) $$

(50)

$$ \frac{\partial f}{{\partial z^{*} }} \triangleq \frac{1}{2}\left( {\frac{\partial f}{{\partial z_{r} }}{ + }j\frac{\partial f}{{\partial z_{i} }}} \right) $$

(51)

In fact, these generalized complex derivatives can be formally implemented by regarding $f(z)$ as a bivariate function $f(z,z^{*} )$ and treating $z$ and $z^{*}$ as independent variables. In other words, when applying $\frac{\partial f}{{\partial z}}$, we take the derivative with respect to $z$, while formally treating $z^{*}$ as a constant. Similarly, $z$ is formally treated as a constant when deriving $\frac{\partial f}{{\partial z^{*} }}$. In particular, if $\frac{\partial f}{{\partial z^{*} }} = 0$, the complex-valued function $f(z)$ becomes complex derivative (analytic). So the Cauchy–Riemann equations can simply be stated as $\frac{\partial f}{{\partial z^{*} }} = 0$. Moreover, Wirtinger calculus contains standard complex calculus as a special case. Finally, according to the rules of CR calculus, its chain rule can be summarized as

$$ \frac{\partial g(f)}{{\partial z}} = \frac{\partial g}{{\partial f}}\frac{{\partial f}}{\partial z} + \frac{\partial g}{{\partial f^{*} }}\frac{{\partial f^{*} }}{\partial z} $$

(52)

$$ \frac{\partial g(f)}{{\partial z^{*} }} = \frac{\partial g}{{\partial f}}\frac{{\partial f}}{{\partial z^{*} }} + \frac{\partial g}{{\partial f^{*} }}\frac{{\partial f^{*} }}{{\partial z^{*} }} $$

(53)