Skip to main content

A Family of Adaptive Volterra Filters Based on Maximum Correntropy Criterion for Improved Active Control of Impulsive Noise

Circuits, Systems, and Signal Processing volume 41, pages 1019–1037 (2022)Cite this article

Abstract

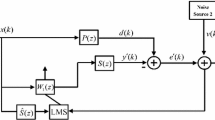
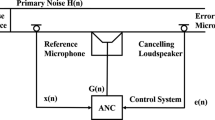
Linear active noise control (ANC) systems have been used in the past to effectively suppress Gaussian noise. A practical ANC system must consider nonlinearities in the secondary path with a non-minimum phase. For an ANC system to effectively operate in a modern-day acoustic environment with multiple electrical/electronic systems operating in the vicinity, the reference noise source is taken as a non-Gaussian stochastic process. Linear systems have shown unacceptable performance in countering the disturbances that are impulsive in nature. Considering these issues, we propose a family of adaptive algorithms for ANC systems that employ a second-order Volterra filter for accurate modeling of the impulsive disturbances. We utilize the maximum correntropy criterion as the cost function to improve the adaptive filtering process, which generates the most appropriate output signal in the ANC system’s successive iterative stages. The proposed algorithms feature dynamic learning-rate parameters, which improve the tracking performance of the algorithms. Also, a careful selection of the Volterra filter’s kernel size in the proposed algorithms ensures a balance between system stability and convergence rate. These parameters are made automatically adjustable, based on the residual error and the reference input signals, to optimize performance in non-Gaussian environments. A comparison of the proposed algorithms with its counterparts is presented through computer simulations in terms of average noise reduction for different levels of impulsive noise. The proposed algorithms are also compared with each other to find the best performing algorithm in a non-Gaussian environment. Achieved results exhibit the effectiveness of the proposed algorithms in their ability to attenuate impulsive noise in comparison with the existing adaptive algorithms for ANC systems. Later, the proposed algorithm has been implemented for speech enhancement, where the noise from the speech sample is identified and removed using an adaptive filter algorithm. Simulations reveal that the devised algorithm can effectively denoise speech signals. Further, in the last part of the paper, the VF-MCCRMC is modified in accordance with the energy of the error signal, and the simulation results demonstrated the improvement in stability and error performance.

This is a preview of subscription content, access via your institution.

Access options

Buy single article

Instant access to the full article PDF.

USD 39.95

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Data Availability Statement

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. M.T. Akhtar, W. Mitsuhashi, A modified normalized FxLMS algorithm for active control of impulsive noise, in 18th IEEE European Signal Processing Conference (2010). p. 1–5

  2. P.E. An, B. Brown, C.J. Harris, On the convergence rate performance of the normalized least-mean-square adaptation. IEEE Trans. Neural Netw. 8(5), 1211–1214 (1997)

    Article  Google Scholar 

  3. L.S. de Assis, Jurair R de P. Junior, L. Tarrataca, D.B. Haddad, Efficient Volterra systems identification using hierarchical genetic algorithms. Appl. Soft Comput. 85, 105745 (2019)

    Article  Google Scholar 

  4. B. Chen, L. Xing, J. Liang, N. Zheng, J.C. Principe, Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion. IEEE Signal Process. Lett. 21(7), 880–884 (2014)

    Article  Google Scholar 

  5. B. Chen, L. Xing, B. Xu, H. Zhao, N. Zheng, J.C. Principe, Kernel risk-sensitive loss: definition, properties and application to robust adaptive filtering. IEEE Trans. Signal Process. 65(11), 2888–2901 (2017)

    Article  MathSciNet  Google Scholar 

  6. W.Y. Chen, R.A. Haddad, A variable step size LMS algorithm, in 33rd Midwest Symposium on Circuits and Systems, vol. 1, (1990). p. 423–426

  7. Z. Dayong, V. DeBrunner, Efficient adaptive nonlinear filters for nonlinear active noise control. IEEE Trans. Circ. Syst. I Regular Paper. 54(3), 669–681 (2007)

    Article  Google Scholar 

  8. N.V. George, G. Panda, A robust filtered-s LMS algorithm for nonlinear active noise control. Appl. Acoust. 73(8), 836–841 (2012)

    Article  Google Scholar 

  9. J.P.F. Guimarães, A.I.R. Fontes, F.B. da Silva, A. de M. Martins, R.V. Borries, Complex correntropy induced metric applied to compressive sensing with complex-valued data, in Southwest Symposium on Image Analysis and Interpretation(SSIAI), IEEE (2018). p. 21–24

  10. D.B. Haddad, M.R. Petraglia, A. Petraglia, A unified approach for sparsity-aware and maximum correntropy adaptive fillters, in 24th IEEE European Signal Processing Conference, (2016). p. 170–174

  11. S.S. Haykin, Adaptive Filter Theory. Prentice-Hall Information and System Sciences Series (Prentice Hall, 1991)

  12. Z. He, H. Ye, E. Li, An efficient algorithm for nonlinear active noise control of impulsive noise. Appl. Acoust. 148, 366–374 (2019)

    Article  Google Scholar 

  13. N.C. Kurian, K. Patel, N.V. George, Robust active noise control: An information theoretic learning approach. Appl. Acoust. 117, 180–184 (2017)

    Article  Google Scholar 

  14. P. Lara, F. Igreja, L.D.T.J. Tarrataca, D.B. Haddad, M.R. Petraglia, Exact expectation evaluation and design of variable step-size adaptive algorithms. IEEE Signal Process. Lett. 26(1), 74–78 (2019)

    Article  Google Scholar 

  15. N. Le Thai, X. Wu, J. Na, Y. Guo, N.T. Tin, P.X. Le, Adaptive variable step-size neural controller for nonlinear feedback active noise control systems. Appl. Acoust. 116, 337–347 (2017)

    Article  Google Scholar 

  16. R. Leahy, Z. Zhou, Y-C. Hsu, Adaptive filtering of stable processes for active attenuation of impulsive noise, in IEEE International Conference on Acoustics, Speech, and Signal Processing, vol. 5, (1995). p. 2983–2986

  17. W. Liu, P.P. Pokharel, J.C. Principe, Correntropy: properties and applications in non-gaussian signal processing. IEEE Trans. Signal Process. 55(11), 5286–5298 (2007)

    Article  MathSciNet  Google Scholar 

  18. L. Lu, H. Zhao, Active impulsive noise control using maximum correntropy with adaptive kernel size. Mech. Syst. Signal Process. 87, 180–191 (2017)

    Article  Google Scholar 

  19. T. Padhi, M. Chandra, A. Kar, Performance evaluation of hybrid active noise control system with online secondary path modeling. Appl. Acoust. 133, 215–226 (2018)

    Article  Google Scholar 

  20. T. Padhi, M. Chandra, A. Kar, M.N.S. Swamy, Design and analysis of an improved hybrid active noise control system. Appl. Acoust. 127, 260–269 (2017)

    Article  Google Scholar 

  21. T. Padhi, M. Chandra, A. Kar, M.N.S. Swamy, A new adaptive control strategy for hybrid narrowband active noise control systems in a multi-noise environment. Appl. Acoust. 146, 355–367 (2019)

    Article  Google Scholar 

  22. E. Parzen, On estimation of a probability density function and mode. Ann. Math. Statist. 33(3), 1065–1076 (1962)

    Article  MathSciNet  Google Scholar 

  23. R.M.S. Pimenta, L.C. Resende, N.N. Siqueira, D.B. Haddad, M.R. Petraglia, A new proportionate adaptive filtering algorithm with coefficient reuse and robustness against impulsive noise, in 26th IEEE European Signal Processing Conference, (2018). p. 465–469

  24. R.A.D. Prado, F.d. R. Henriques, D.B. Haddad, Sparsity-aware distributed adaptive filtering algorithms for nonlinear system identification, in International Joint Conference on Neural Networks (IJCNN) (2018). p. 1–8

  25. M. Shao, C.L. Nikias, Signal processing with fractional lower order moments: stable processes and their applications. Proc. IEEE 81(7), 986–1010 (1993)

    Article  Google Scholar 

  26. B.W. Silverman, Density Estimation for Statistics and Data Analysis (Routledge, 2018)

  27. J.V.G. de Souza, D.B. Haddad, F.D.R. Henriques, M.R. Petraglia, Novel proportionate adaptive filters with coefficient vector reusing. Circ. Syst. Signal Process. 39(5), 2473–2488 (2019)

    Article  Google Scholar 

  28. L. Tan, J. Jiang, Adaptive second-order Volterra filtered-x RLS algorithms with sequential and partial updates for nonlinear active noise control, in IEEE Conference on Industrial Electronics and Applications (2009). p. 1625–1630

  29. L. Tan, J. Jiang, Adaptive Volterra filters for active control of nonlinear noise processes. IEEE Trans. Signal Process. 49(8), 1667–1676 (2001)

    Article  Google Scholar 

  30. Y. Wang, C. Li, C. Tian, Modified recursive least squares algorithm for sparse system identification, in 7th IEEE International Conference on Modelling, Identification and Control (ICMIC), IEEE (2015). p. 1–5

  31. L. Wu, H. He, X. Qiu, An active impulsive noise control algorithm with logarithmic transformation. IEEE Trans. Audio Speech Language Process. 19(4), 1041–1044 (2010)

    Article  Google Scholar 

  32. H. Zhao, X. Zeng, Z. He, T. Li, Adaptive RSOV filter using the FELMS algorithm for nonlinear active noise control systems. Mech. Syst. Signal Process. 34(1–2), 378–392 (2013)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Indian Institute of Information Technology, Design and Manufacturing, Kancheepuram, India

    Guttikonda Gowtham, Srikanth Burra & Asutosh Kar

  2. Department of Electronic Systems, Aalborg University, Aalborg, Denmark

    Jan Østergaard

  3. Department of Computer Engineering, King Mongkut’s Institute of Technology Ladkrabang, Bangkok, Thailand

    Pitikhate Sooraksa

  4. Faculty of Technical Sciences in Cacak, University of Kragujevac, Kragujevac, Serbia

    Vladimir Mladenovic

  5. CEFET/RJ, Rio de Janeiro, Brazil

    Diego B. Haddad

Authors
  1. Guttikonda Gowtham
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Srikanth Burra
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Asutosh Kar
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jan Østergaard
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Pitikhate Sooraksa
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Vladimir Mladenovic
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Diego B. Haddad
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Asutosh Kar.

Ethics declarations

Conflict of interest

The authors declared that they have no conflicts of interest to this work.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Gowtham, G., Burra, S., Kar, A. et al. A Family of Adaptive Volterra Filters Based on Maximum Correntropy Criterion for Improved Active Control of Impulsive Noise. Circuits Syst Signal Process 41, 1019–1037 (2022). https://doi.org/10.1007/s00034-021-01821-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-021-01821-7

Keywords

  • Volterra filter
  • Nonlinear path
  • Impulsive noise
  • Correntropy