Skip to main content
SpringerLink
Log in

Reverse Converters for the Moduli Set {\(2^{n}, 2^{n-1}-1,2^{n}-1, 2^{n+1}-1\}(n\,\hbox {Even})\)

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

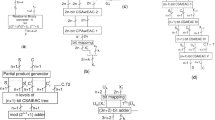
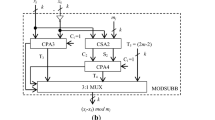
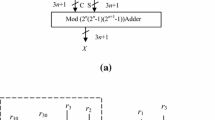
In this paper, two residue number system (RNS) to binary converters for the moduli set {\(2^{n}, 2^{n-1}-1,2^{n}-1, 2^{n+1}-1\}\) for (n even) are presented. One of them uses a two-level conversion, in which, in the first level, two pairs of moduli are considered to obtain two intermediate decoded numbers. A second-level converter obtains the final decoded number corresponding to these two intermediate decoded numbers. Both levels use mixed radix conversion. The second proposed RNS to binary converter uses the conventional MRC of the four-moduli set. The proposed converters are compared with previously reported conversion techniques for this moduli set and converters for other four, five and eight moduli sets for realizing similar dynamic ranges regarding hardware requirement and conversion time. The hardware resource requirement (A), conversion time (T), AT and \(AT^{2}\) trade-offs are discussed to bring out the relative advantages of various converters. The proposed converters have been shown to need less hardware or less conversion time than the other some of the reported converters for this moduli set. It has been shown by detailed comparison that converters using conjugate moduli and vertical extension generally exhibit better performance (lower hardware /lower conversion time) than those using no vertical extension, while needing differing word lengths of various moduli. These, however, need slightly complex multipliers/adders in the \((2^{n} +1)\) channel. Implementation results on FPGA of the proposed converters for few dynamic ranges also have been presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. P.V. Ananda Mohan, Residue Number Systems: Algorithms and Architectures (Kluwer Academic Publishers, New York, 2002)

    Book  Google Scholar 

  2. P.V. Ananda Mohan, RNS to binary converter for the new three moduli set \(2^{n+1} -1, 2^{n}, 2^{n}-1\). IEEE Trans. Circuits Syst. II Express Brief 54(9), 775–779 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  3. P.V. Ananda Mohan, New reverse converters for the moduli set \(2^{n}-3, 2^{n}+1, 2^{n}-1, 2^{n}+3\). AEU 62, 643–658 (2008)

    Google Scholar 

  4. P.V. Ananda Mohan, A.B. Premkumar, RNS to Binary converters for two four moduli sets \(2^{n}-1, 2^{n}, 2^{n}+1, 2^{n+1}-1 \) and \(2^{n}-1, 2^{n}, 2^{n}+1, 2^{n+1}+1\). IEEE Trans. Circuits Syst. I 54, 1245–1254 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  5. M. Bhardwaj, T. Srikanthan , C.T. Clarke, A reverse converter for the 4 moduli super set \(2^{n}-1, 2^{n}, 2^{n}+1, 2^{n+1}+1\), in IEEE Conference on Computer Arithmetic (1999), pp. 168–175

  6. B. Cao, T. Srikanthan, C.H. Chang, Efficient reverse converters for the four-moduli sets \(2^{n}-1, 2^{n}, 2^{n}+1, 2^{n+1}-1\) and \(2^{n}-1, 2^{n}, 2^{n}+1, 2^{n-1}-1\). IEE Proc. Comput. Digit. Tech. 152, 687–696 (2005)

    Article  MATH  Google Scholar 

  7. B. Cao, C.H. Chang, T. Srikanthan, An efficient reverse converter for the 4-moduli set \(2^{n}-1, 2^{n}, 2^{n}+1, 2^{2n}+1\) based on the new Chinese remainder theorem. IEEE Trans. Circuits Syst. I 50, 1296–1303 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  8. B. Cao, C.H. Chang, T. Srikanthan, A residue to binary converter for a new five-moduli set. IEEE Trans. Circuits Syst. I 54, 1041–1049 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  9. G. Chalivendra, V. Hanumaiah, S. Vrudhula, A new balanced 4-moduli set \(2^{k}, 2^{n}-1, 2^{n}+1, 2^{n+1}-1\) and its reverse converter design for efficient reverse converter implementation, in Proceedings of ACM GSVLSI, (Lausanne, Switzerland, 2011), pp. 139–144

  10. A. Dhurkadas, Comments on A high-speed realization of a residue to binary number system converter. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 45(3), 446–447 (1998)

    Article  Google Scholar 

  11. L.S. Didier, P.Y. Rivaille, A generalization of a fast RNS conversion for a new 4-modulus base. IEEE Trans. Circuits Syst. II Express Br. 56, 46–50 (2009)

    Article  Google Scholar 

  12. M. Esmaeildoust, K. Navi, M. Taheri, A.S. Molahosseini, S. Khodambashi, Efficient RNS to binary converters for the new 4-moduli set \(2^{n}, 2^{n+1} -1, 2^{n}-1, 2^{n-1} -1\). IEICE Electron. Express 9(1), 1–7 (2012)

    Article  Google Scholar 

  13. M. Esmaeildoust, D. Schinianakis, H. Javashi, T. Stouraitis, K. Navi, Efficient RNS implementation of elliptic curve point multiplication over GF(\(p)\). IEEE Trans. VLSI Syst. 21, 1545–1549 (2013)

    Article  Google Scholar 

  14. A.A. Hiasat, VLSI implementation of new arithmetic residue to binary decoders. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 13, 153–158 (2005)

    Article  Google Scholar 

  15. M. Hosseinzadeh, A. Molahosseini, K. Navi, An improved reverse converter for the moduli set \(2^{n}+1, 2^{n}-1, 2^{n}, 2^{n+1}-1\). IEICE Electron. Express 5, 672–677 (2008)

    Article  Google Scholar 

  16. G. Jaberipur, H. Ahmadifar, A ROM-less reverse converter for moduli set \(2^{q}\pm 1, 2^{q}\pm 3\). IET Comput. Digit. Tech. 8, 11–22 (2014)

    Article  Google Scholar 

  17. A.S. Molahosseini, K. Navi, C. Dadkhah, O. Kavehei, S. Timarchi, Efficient reverse converter designs for the new 4-moduli sets \(2^{n}-1, 2^{n}, 2^{n}+1, 2^{2n+1}-1\) and \(2^{n}-1, 2^{n}+1, 2^{2n}, 2^{2n}+1\) based on new CRTs. IEEE Trans. Circuits Syst. I 57, 823–835 (2010)

    Article  MathSciNet  Google Scholar 

  18. A. Omondi, B. Premkumar, Residue Number Systems: Theory and Implementation (Imperial College Press, London, 2007)

    Book  MATH  Google Scholar 

  19. P. Patronik, S.J. Piestrak, Design of reverse converters for the new RNS moduli set \(2^{n}+1, 2^{n}, 2^{n}-1, 2^{n-1} +1\) (\(n\) odd). IEEE Trans. Circuits Syst. I 61, 3436–3449 (2014)

    Article  MATH  Google Scholar 

  20. P. Patronik, S.J. Piestrak, Design of reverse converters for general RNS moduli sets \(2^{k}, 2^{n}-1, 2^{n}+1, 2^{n+1}-1\) and \(2^{k}, 2^{n}-1, 2^{n}+1, 2^{n-1}-1\) (\(n\) even). IEEE Trans. Circuits Syst. I 61, 1687–1700 (2014)

    Article  MATH  Google Scholar 

  21. H. Pettenghi, R. Chaves, L. Sousa, Method to design general RNS converters for extended moduli sets. IEEE Trans. Circuits Syst. II 60, 877–881 (2013)

    Article  Google Scholar 

  22. H. Pettenghi, R. Chaves, L. Sousa, RNS reverse converters for moduli sets with dynamic ranges up to (8\(n\)+1) bits. IEEE Trans. Circuits Syst. 60, 1487–1500 (2013)

    Article  MathSciNet  Google Scholar 

  23. S.J. Piestrak, A high-speed realization of residue to binary system converter. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 42(10), 661–663 (1995)

    Article  Google Scholar 

  24. A. Skavantzos, T. Stouraitis, Grouped-moduli residue number systems for fast signal processing, in Proceedings of IEEE ISCAS (1999), pp. 478–483

  25. A. Skavantzos, M. Abdallah, Implementation issues of the two-level residue number system with pairs of conjugate moduli. IEEE Trans. Signal Process. 47, 826–838 (1999)

    Article  Google Scholar 

  26. A. Skavantzos, M. Abdallah, T. Stouraitis, D. Schinianakis, Design of a balanced 8-modulus RNS, in Proceedings of IEEE ISCAS (2009), pp. 61–64

  27. M.H. Sheu, S.H. Lin, C. Chen, S.W. Yang, An efficient VLSI design for a residue to binary converter for general balance moduli (\(2^{n}-3, 2^{n}-1, 2^{n}+1, 2^{n}+3\)). IEEE Trans. Circuits Syst. Express Br. 51, 52–55 (2004)

    Google Scholar 

  28. M.A. Soderstrand, W.K. Jenkins, G.A. Jullien, F.J. Taylor, Residue Number System Arithmetic: Modern Applications in Signal Processing (IEEE Press, New York, 1986)

    MATH  Google Scholar 

  29. L. Sousa, S. Antao, R. Chaves, On the design of RNS reverse converters for the four-moduli set \(2^{n}+1, 2^{n}-1, 2^{n}, 2^{n+1}+1\). IEEE Trans. VLSI Syst. 21, 1945–1949 (2013)

    Article  Google Scholar 

  30. L. Sousa, S. Antao, MRC based RNS reverse converters for the four-moduli sets \(2^{n}+1,2^{n}-1,2^{n}, 2^{2n+1}-1\) and \(2^{n}+1,2^{n}-1,2^{2n}, 2^{2n+1}-1\). IEEE Trans. Circuits Syst. II 59, 244–248 (2012)

    Article  Google Scholar 

  31. N. Stamenkovic, B. Jovanovic, Reverse converter design for the 4-moduli set \(2^{n}-1,2^{n},2^{n}+1,2^{2n+1}-1\) based on the mixed-radix conversion. Facta Univ. (NIS) Ser. Electron. Energ. 24, 91–105 (2011)

    Google Scholar 

  32. N.S. Szabo, R.I. Tanaka, Residue Arithmetic and Its Applications to Computer Technology (Mc-Graw Hill, New York, 1967)

    MATH  Google Scholar 

  33. M.R. Taheri, N. Shafiee, M. Esmaeildoust, Z. Amirjamshidi, R. Sabbaghi-nadooshan, K. Navi, A high speed residue-to-binary converter for balanced 4-moduli set. J. Comput. Secur. 2, 43–54 (2015)

    Google Scholar 

  34. A. Tyagi, A reduced-area scheme for carry-select adders. IEEE Trans. Comput. 42, 1163–1170 (1993)

    Article  Google Scholar 

  35. A.P. Vinod, A.B. Premkumar, A residue to binary converter for the 4-moduli superset \(2^{n}-1, 2^{n}, 2^{n}+1, 2^{n+1}-1\). JCSC 10, 85–99 (2000)

    Google Scholar 

  36. Y. Wang, X. Song, M. Aboulhamid, H. Shen, Adder-based residue to binary number converters for \(2^{n+}1 -1, 2^{n}, 2^{n}-1\). IEEE Trans. Signal Process. 50(7), 1772–1779 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  37. Z. Wang, G.A. Jullien, W.C. Miller, An improved residue to binary converter. IEEE Trans. Circuits Syst. I 47, 1437–1440 (2000)

    MathSciNet  MATH  Google Scholar 

  38. Y. Wang, Residue to binary converters based on new Chinese remainder theorems. IEEE Trans. Circuits Syst. II 47, 197–205 (2000)

    Article  MATH  Google Scholar 

  39. M. Wesolowski, P. Patronik, K. Berezowski, J. Biernat, Design of a novel flexible 4-moduli RNS and reverse converter, in Proceedings of Signals and Systems Conference (IS SC 2012), IET Irish, IET (2012), pp 1–6

  40. W. Zhang, P. Siy, An efficient design of residue to binary converter for the moduli set \(2^{n}-1, 2^{n}+1, 2^{2n}-2, 2^{2n+1}-3\) based on new CRT II. Elsevier J. Inf. Sci. 178, 264–279 (2008)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Centre For Development of Advanced Computing, Knowledge Park, #1,Old Madras Road, Byappanahalli, Bangalore, 560 038, India

    P. V. Ananda Mohan

Authors
  1. P. V. Ananda Mohan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. V. Ananda Mohan.

Appendix

Appendix

In this Appendix, we consider the two different pairings of moduli in the two-level MRC. In the case of the pairing of Moduli \(M_{13}, M_{24}\), the various multiplicative inverses are as follows:

In the first level we have \(\mathop {\left( {\frac{1}{\mathop 2\nolimits ^n }} \right) }\nolimits _{\mathop 2\nolimits ^n -1} =1\) and \(\mathop {\left( {\frac{1}{\mathop 2\nolimits ^{n-1} -1}} \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1} =\frac{\mathop 2\nolimits ^{n+1} -5}{3}=\mathop 2\nolimits ^{n-1} +\mathop 2\nolimits ^{n-3} +\cdots +\mathop 2\nolimits ^3 +1\) and in the second level, we have \(\mathop {\left( {\frac{1}{\mathop {(2}\nolimits ^{n-1} -1)(\mathop 2\nolimits ^{n+1} -1)}} \right) }\nolimits _{\mathop {\mathop 2\nolimits ^n (2}\nolimits ^n -1)} =\mathop 2\nolimits ^{2n-1} -7\times \mathop 2\nolimits ^{n-1} +1=\mathop 2\nolimits ^{n-1} (\mathop 2\nolimits ^n -7)+1\). This has been derived using extended Euclid algorithm. Thus, in the first level, multiplication with one of the multiplicative inverses takes more time than in the case of choice of \(M_{12}\),\(M_{34}\). In the second level, the multiplicative inverse has (\(n-1\)) number of bits which are “1” and hence (\(n-1\)) partial products are needed to be added. The modulo \(M_{13 }\) reduction can follow a similar method as described in the case of mod \(M_{12}\) reduction.

In the case of the pairing of Moduli \(M_{14}, M_{23}\), the various multiplicative inverses are as follows:

In the first level, we have \(\mathop {\left( {\frac{1}{\mathop 2\nolimits ^n }} \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1} =2\) and \(\mathop {\left( {\frac{1}{\mathop 2\nolimits ^{n-1} -1}} \right) }\nolimits _{\mathop 2\nolimits ^n -1} =-2\). In the second level, we have \(\mathop {\left( {\frac{1}{\mathop {(2}\nolimits ^{n-1} -1)(\mathop 2\nolimits ^n -1)}} \right) }\nolimits _{\mathop {\mathop 2\nolimits ^n (2}\nolimits ^{n+1} -1)} =\frac{\mathop 2\nolimits ^{2n} +19\times \mathop 2\nolimits ^{n-1} +3}{3}=\mathop 2\nolimits ^{n-1} (\mathop 2\nolimits ^{n-1} +\mathop 2\nolimits ^{n-3} +\cdots +\mathop 2\nolimits ^4 +1)+1\). This has been obtained using extended Euclid algorithm.

The multiplicative inverses in the first level are simple, whereas that in the second level has \((n/2)+1\) bits which are “1,” thus leading to \((n/2)+1\) partial products which need to be reduced mod \(M_{14}\) following a similar method as described in the case of mod \(M_{12}\) reduction.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ananda Mohan, P.V. Reverse Converters for the Moduli Set {\(2^{n}, 2^{n-1}-1,2^{n}-1, 2^{n+1}-1\}(n\,\hbox {Even})\) . Circuits Syst Signal Process 37, 3605–3634 (2018). https://doi.org/10.1007/s00034-017-0725-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-017-0725-0

Keywords

Search

Navigation