Abstract
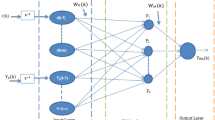
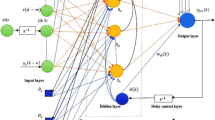
In this research, we propose a novel algorithm for learning of the recurrent neural networks called as the fractional back-propagation through time (FBPTT). Considering the potential of the fractional calculus, we propose to use the fractional calculus-based gradient descent method to derive the FBPTT algorithm. The proposed FBPTT method is shown to outperform the conventional back-propagation through time algorithm on three major problems of estimation namely nonlinear system identification, pattern classification and Mackey–Glass chaotic time series prediction.















Similar content being viewed by others
References
J. Ahmad, Design of Efficient Adaptive Beamforming Algorithms for Novel Mimo Architectures, Ph.D. Thesis, Iqra University, Karachi (2014)
J. Amhad, M. Usman, S. Khan, I. Naseem, H.J. Syed, Rvp-flms: a robust variable power fractional lms algorithm, in 2016 IEEE International Conference on Control System, Computing and Engineering (ICCSCE), IEEE, 2016
J. An, S. Cho, Hand motion identification of grasp-and-lift task from electroencephalography recordings using recurrent neural networks, in 2016 International Conference on Big Data and Smart Computing (BigComp), IEEE, 2016, pp. 427–429
E.A. Antonelo, E. Camponogara, A. Plucenio, System identification of a vertical riser model with echo state networks. IFAC PapersOnLine 48(6), 304–310 (2015)
G. Bao, Z. Zeng, Global asymptotical stability analysis for a kind of discrete-time recurrent neural network with discontinuous activation functions. Neurocomputing 193, 242–249 (2016)
G.W. Bohannan, Analog fractional order controller in temperature and motor control applications. J. Vib. Control 14(9–10), 1487–1498 (2008)
J. Cervera, A. Baños, Automatic loop shaping in qft using crone structures. J. Vib. Control 14(9–10), 1513–1529 (2008)
W. Chan, N. Jaitly, Q.V. Le, O. Vinyals, Listen, attend and spell: a neural network for large vocabulary conversational speech recognition, in 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2016
N.I. Chaudhary, M.A.Z. Raja, M.S. Aslam, N. Ahmed, Novel generalization of volterra lms algorithm to fractional order with application to system identification. Neural Comput. Appl. (2016). doi:10.1007/s00521-016-2548-5
X. Chen, T. Tan, X. Liu, P. Lanchantin, M. Wan, M.J. Gales, P.C. Woodland, Recurrent neural network language model adaptation for multi-genre broadcast speech recognition, in Proceedings of ISCA Interspeech, Dresden, Germany, 2015, pp. 3511–3515
L. Debnath, Recent applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. 2003(54), 3413–3442 (2003)
K. Doya, S. Yoshizawa, Adaptive neural oscillator using continuous-time back-propagation learning. Neural Netw. 2(5), 375–385 (1989)
M. Fairbank, E. Alonso, D. Prokhorov, An equivalence between adaptive dynamic programming with a critic and backpropagation through time. IEEE Trans. Neural Netw. Learn. Syst. 24(12), 2088–2100 (2013)
Z. Gan, C. Li, R. Henao, D.E. Carlson, L. Carin, Deep temporal sigmoid belief networks for sequence modeling, in Advances in Neural Information Processing Systems 28, eds. by C. Cortes, N.D. Lawrence, D.D. Lee, M. Sugiyama, R. Garnett (Curran Associates, Inc., 2015), pp. 2467–2475
K. George, K. Subramanian, N. Sheshadhri, Improving transient response in adaptive control of nonlinear systems. IFAC PapersOnLine 49(1), 658–663 (2016)
T.R. Golub, D.K. Slonim, P. Tamayo, C. Huard, M. Gaasenbeek, J.P. Mesirov, H. Coller, M.L. Loh, J.R. Downing, M.A. Caligiuri et al., Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 286(5439), 531–537 (1999)
I. Grau, G. Nápoles, I. Bonet, M.M. García, Backpropagation through time algorithm for training recurrent neural networks using variable length instances. Comput. Sist. 17(1), 15–24 (2013)
S.O. Haykin, Neural Networks: A Comprehensive Foundation (Prentice Hall PTR, Upper Saddle River, 1994)
M. Hermans, J. Dambre, P. Bienstman, Optoelectronic systems trained with backpropagation through time. IEEE Trans. Neural Netw. Learn. Syst. 26(7), 1545–1550 (2015)
M. Hermans, M. Soriano, J. Dambre, P. Bienstman, I. Fischer, Photonic delay systems as machine learning implementations. arXiv preprint arXiv:1501.02592 (2015)
H. Jaeger, Tutorial on training recurrent neural networks, covering BPPT, RTRL, EKF and the “echo state network” approach, GMD Report 159, (German National Research Center for Information Technology, 2002), p. 48
Y. Ji, G. Haffari, J. Eisenstein, A latent variable recurrent neural network for discourse relation language models. arXiv preprint arXiv:1603.01913 (2016)
H. Jia, Investigation into the effectiveness of long short term memory networks for stock price prediction. arXiv preprint arXiv:1603.07893 (2016)
A. Joulin, T. Mikolov, Inferring algorithmic patterns with stack-augmented recurrent nets, in Advances in Neural Information Processing Systems 28, eds. by C. Cortes, N.D. Lawrence, D.D. Lee, M. Sugiyama, R. Garnett (Curran Associates, Inc., 2015), pp. 190–198
G. Jumarie, Modified Riemann–Liouville derivative and fractional taylor series of nondifferentiable functions further results. Comput. Math. Appl. 51(9), 1367–1376 (2006)
G. Jumarie, Table of some basic fractional calculus formulae derived from a modified Riemann–Liouville derivative for non-differentiable functions. Appl. Math. Lett. 22(3), 378–385 (2009)
G. Jumarie, An approach via fractional analysis to non-linearity induced by coarse-graining in space. Nonlinear Anal. Real World Appl. 11(1), 535–546 (2010)
G. Jumarie, On the derivative chain-rules in fractional calculus via fractional difference and their application to systems modelling. Open Phys. 11(6), 617–633 (2013)
C. Junhua, D. Baorong, S. Guangren, A novel time-series artificial neural network: a case study for forecasting oil production. Sci. J. Control Eng. 6(1), 1–7 (2016)
F. Ken-ichi, N. Yuichi, Approximation of dynamical systems by continuous time recurrent neural networks. Neural Netw. 6, 801–806 (1993). doi:10.1016/S0893-6080(05)80125-X
S. Khan, I. Naseem, R. Togneri, M. Bennamoun, A novel adaptive kernel for the rbf neural networks. Circuits Syst. Signal Process. 36(4), 1639–1653 (2017). doi:10.1007/s00034-016-0375-7
M. Kleinz, T. Osler, A childs garden of fractional derivatives. The College Math Journal 31(2), 82–88 (2000)
J. Koscak, R. Jaksa, P. Sincák, Prediction of temperature daily profile by stochastic update of backpropagation through time algorithm. J. Math. Syst. Sci. 2(4), 217–225 (2012)
B. Krishna, K. Reddy, Active and passive realization of fractance device of order 1/2. Active Passive Electron. Compon. 2008, 369421 (2008). doi:10.1155/2008/369421
Q.V. Le, A Tutorial on Deep Learning Part 2: Autoencoders, Convolutional Neural Networks and Recurrent Neural Networks (Stanford University Department of Computer Science, CA, 2015)
Q.V. Le, N. Jaitly, G.E. Hinton, A simple way to initialize recurrent networks of rectified linear units. arXiv preprint arXiv:1504.00941 (2015)
M.F. Lima, J.A.T. Machado, M.M. Crisóstomo, Experimental signal analysis of robot impacts in a fractional calculus perspective. JACIII 11(9), 1079–1085 (2007)
J. Lovoie, T.J. Osler, R. Tremblay, Fractional derivatives and special functions. SIAM Rev. 18(2), 240–268 (1976)
R. Magin, M. Ovadia, Modeling the cardiac tissue electrode interface using fractional calculus. J. Vib. Control 14(9–10), 1431–1442 (2008)
A. Mazumder, A. Rakshit, D. Tibarewala, A back-propagation through time based recurrent neural network approach for classification of cognitive eeg states, in 2015 IEEE International Conference on Engineering and Technology (ICETECH), IEEE, 2015, pp. 1–5
T. Mikolov, A. Joulin, S. Chopra, M. Mathieu, M. Ranzato, Learning longer memory in recurrent neural networks. arXiv preprint arXiv:1412.7753 (2014)
P.K. Muthukumar, A.W. Black, Recurrent neural network postfilters for statistical parametric speech synthesis. arXiv preprint arXiv:1601.07215 (2016)
R. Panda, M. Dash, Fractional generalized splines and signal processing. Signal Process. 86(9), 2340–2350 (2006)
G. Parascandolo, H. Huttunen, T. Virtanen, Recurrent neural networks for polyphonic sound event detection in real life recordings. arXiv preprint arXiv:1604.00861 (2016)
H. Peng, F. Long, C. Ding, Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 27(8), 1226–1238 (2005)
Y. Pu, X. Yuan, K. Liao, J. Zhou, N. Zhang, X. Pu, Y. Zeng, A recursive two-circuits series analog fractance circuit for any order fractional calculus, in ICO20: Optical Information Processing, 60271Y (2006). doi:10.1117/12.668189
M.A.Z. Raja, N.I. Chaudhary, Two-stage fractional least mean square identification algorithm for parameter estimation of carma systems. Signal Process. 107, 327–339 (2015)
S. Ravuri, A. Stolcke, Recurrent neural network and lstm models for lexical utterance classification, in Sixteenth Annual Conference of the International Speech Communication Association, 2015
Y. Roudi, G. Taylor, Learning with hidden variables. Curr. Opin. Neurobiol. 35, 110–118 (2015)
J. Sabatier, O.P. Agrawal, J.T. Machado, Advances in Fractional Calculus (Springer, Berlin, 2007)
S. Saha, G. Raghava, Prediction of continuous b-cell epitopes in an antigen using recurrent neural network. Proteins Struct. Funct. Bioinform. 65(1), 40–48 (2006)
H. Sak, A. Senior, K. Rao, F. Beaufays, Fast and accurate recurrent neural network acoustic models for speech recognition. arXiv preprint arXiv:1507.06947 (2015)
B. Shoaib, I.M. Qureshi, Shafqatullah, Ihsanulhaq, Adaptive step-size modified fractional least mean square algorithm for chaotic time series prediction. Chin. Phys. B 23(5), 050503 (2014)
L. Sommacal, P. Melchior, A. Oustaloup, J.M. Cabelguen, A.J. Ijspeert, Fractional multi-models of the frog gastrocnemius muscle. J. Vib. Control 14(9–10), 1415–1430 (2008)
L. Sun, S. Kang, K. Li, H. Meng, Voice conversion using deep bidirectional long short-term memory based recurrent neural networks, in 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, 2015, pp. 4869–4873
W. Sun, H. Gao, O. Kaynak, Finite frequency \(h_{\infty }\) control for vehicle active suspension systems. IEEE Trans. Control Syst. Technol. 19(2), 416–422 (2011). doi:10.1109/TCST.2010.2042296
W. Sun, Y. Zhang, Y. Huang, H. Gao, O. Kaynak, Transient-performance-guaranteed robust adaptive control and its application to precision motion control systems. IEEE Trans. Ind. Electron. 63(10), 6510–6518 (2016)
W. Sun, Y. Zhao, J. Li, L. Zhang, H. Gao, Active suspension control with frequency band constraints and actuator input delay. IEEE Trans. Ind. Electron. 59(1), 530–537 (2012)
M. Sundermeyer, I. Oparin, J.L. Gauvain, B. Freiberg, R. Schluter, H. Ney, Comparison of feedforward and recurrent neural network language models, in 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, 2013, pp. 8430–8434
Y. Tan, Z. He, B. Tian, A novel generalization of modified lms algorithm to fractional order. IEEE Signal Process. Lett. 22(9), 1244–1248 (2015)
N.T. Vu, P. Gupta, H. Adel, H. Schütze, Bi-directional recurrent neural network with ranking loss for spoken language understanding, in 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2016
M. Weilbeer, Efficient numerical methods for fractional differential equations and their analytical background. Papierflieger (Braunschweig University of Technology, Braunschweig, 2005)
C. Weng, D. Yu, S. Watanabe, B.H.F. Juang, Recurrent deep neural networks for robust speech recognition, in 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, 2014, pp. 5532–5536
T. Wigren, Recursive prediction error identification and scaling of non-linear state space models using a restricted black box parameterization. Automatica 42(1), 159–168 (2006)
T. Wigren, J. Schoukens, Three free data sets for development and benchmarking in nonlinear system identification, in Control Conference (ECC), 2013 European, IEEE, 2013, pp. 2933–2938
R.J. Williams, J. Peng, An efficient gradient-based algorithm for on-line training of recurrent network trajectories. Neural Comput. 2(4), 490–501 (1990)
R.J. Williams, D. Zipser, Gradient-based learning algorithms for recurrent networks and their computational complexity. Backpropagation Theory Archit. Appl. 1, 433–486 (1995)
W. Zaremba, I. Sutskever, O. Vinyals, Recurrent neural network regularization. arXiv preprint arXiv:1409.2329 (2014)
M. Zhang, Z. McCarthy, C. Finn, S. Levine, P. Abbeel, Learning deep neural network policies with continuous memory states. arXiv preprint arXiv:1507.01273 (2015)
S. Zheng, S. Jayasumana, B. Romera-Paredes, V. Vineet, Z. Su, D. Du, C. Huang, P.H. Torr, Conditional random fields as recurrent neural networks, in Proceedings of the IEEE International Conference on Computer Vision, 2015, pp. 1529–1537
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Khan, S., Ahmad, J., Naseem, I. et al. A Novel Fractional Gradient-Based Learning Algorithm for Recurrent Neural Networks. Circuits Syst Signal Process 37, 593–612 (2018). https://doi.org/10.1007/s00034-017-0572-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-017-0572-z