On Digital Realizations of Non-integer Order Filters

Abstract

Typical approach to non-integer order filtering consists of analogue design and implementation. Digital realization of non-integer order systems is susceptible to problems such as infinite memory requirement and sensitivity to numerical errors. The aim of this paper is to present two efficient methods for digital realization of non-integer order filters: discrete time-domain Oustaloup approximation and Laguerre impulse response approximation. Properties of both methods are investigated with use of non-integer low-pass filter. Filters realized with presented methods are then used for filtering of EEG signal. Paper concludes with discussion of merits and flaws of both methods.

1 Introduction

Non-integer (fractional) order systems are a rapidly growing field of interest for both mathematicians and engineers. One of the intensively analyzed aspects of this domain is non-integer order filters. One can observe that the theory of such filters is relatively well grounded; however, many problems of implementation are still open. A need for efficient implementation is obvious as potential applications are numerous in areas such as telecommunication, biomedical engineering, control and many others.

In this paper, the authors focus on efficient methods of creating discrete realizations of filters that do not have the burden of infinite memory and provide good representation of non-integer order filter frequency characteristics. In order to do so, two methods are proposed resulting in approximations in the form of discrete state- space systems. These methods are discrete time-domain Oustaloup approximation and Laguerre impulse response approximation (LIRA).

The problem of approximating the non-integer order system with an integer order one is being analyzed from many years. Most popular approaches are based on using Oustaloup transfer function approximation or Continuous Fraction Expansion (CFE) in the domain of transfer functions. Both of these methods were used for approximating integrators. The problem is that Oustaloup method is very sensitive to high discretization frequencies and rounding errors. It was observed in earlier authors’ works [7] that it can become destabilized very easily. On the other hand, CFE method shows inferior quality in frequency characteristic representation [25]. Detailed analysis of CFE approximation in discrete time can be found in [12, 44, 45].

The first method used in this article, the Oustaloup method, is used in the literature in two different, yet equivalent, versions. The original approach, developed by Oustaloup [26, 27], is based on approximation of fractional systems in frequency domain. This approach is widely used, e.g., [11, 22, 25, 32] and many others. However, this method has some flaws which cannot be neglected—when discretized, it does not guarantee stability of the system (the poles of discrete system are outside unit circle) (see, e.g., [30]). In order to avoid, i.e., numerical issues induced by this method, another kind of approximation was proposed—instead of transfer function, the state-space approach is considered. State-space realization of Oustaloup transfer function was considered in, e.g., [23, 36, 39, 40]; however, its discrete properties were not considered in this context. In this paper, the method from [7] is used. This approach allows avoiding numerical problems observed in practical realization. The proposed approach is to realize every block of the transfer function in form of a state-space system. Those first-order systems will be then collected in a single matrix resulting in full matrix realization. The results were first presented in authors’ earlier works [7] and [6]. This approach proved to be more robust to different discretization schemes. The superiority of this approach was then validated with real-time control experiments—magnetic levitation control [10] and air heater control [9].

The other method considered in this paper, Laguerre impulse response approximation (LIRA), chosen by authors to analyze fractional filters uses approximation with (orthonormal) Laguerre functions. Some works, concerning this type of approximation, are, e.g., [3, 24]. The authors’ approach was developed independently in [5]. It introduces substantial improvements such as $\mathcal {L}^1$ convergence, estimation of approximation error and choice of optimal approximation basis. For examples of use, see [46–48].

The most important results on non-integer order filters come from analog filtering theory. In [34], Radwan et al. generalize standard second-order filters. In particular, they analyze filters of various characteristics (i.e., low pass, high pass, band pass, notch) constructed using two fractional-order capacitors of order $\alpha$. In [2], Soltan Ali et al. describe a transformation of Butterworth filter to non-integer order domain. They present both analytical and numerical results combined with Advanced Design System simulation. The result was a filter with more degrees of freedom than classical filter and therefore with better design flexibility. In [17], Freeborn et al. presented fractional two-step Tow-Thomas biquad filter. They used an approximation of fractional-order capacitors in form of integer order transfer function. The results for low-pass and asymmetric band-pass filters are verified both with MATLAB and PSPICE, and with physical experiments using non-integer order capacitors. Another example of second-order filter generalization was described by Tripathy et al. [42]. Unlike earlier works, this paper uses two fractional-order capacitors with different orders. Experimental results were also compared with simulation (MATLAB, PSPICE), along with some analysis concerning stability of the filter and its sensitivity. In [35], the non-integer RLC filter is considered. The authors, A. G. Radwan and M. E. Fouda, use a gradient-based optimization technique to find optimal parameters in the frequency domain. They describe the performance of such filters along with some new issues which need resolving when designing non-integer order filters. Important results come from attempts to directly implement the non-integer order filters. For example, in [33], we can find an analysis of non-integer order oscillators. Radwan et al. derive there the Barkhausen condition for non-integer order system to oscillate. They also verify numerically the results as examples taking, i.e., Wien oscillator, Colpitts oscillator and phase-shift oscillator. In [1], we see new techniques for implementing continuous-time second-order band-pass filters with high-quality factors and asymmetric slopes using multiple amplifier biquads and frequency-dependent negative resistor. Ahmadi et al. present there four possible realizations of the filters: one based on a frequency-dependent negative resistor (FDNR), another based on an inductor and two based on multiple amplifier biquads (MABs). In [41], there are another examples of design and implementation of fractional-order filters, along with performance analysis—in both simulation and experiment. This research stated clearly the superiority of non-integer order systems over classical systems. Tsirimokou et al [43] analyzed the behavior of so-called companding filters in low-voltage environment also using alternative domain, $\sinh$ instead of classic $\log$-one. In [16], Freeborn et al. propose the use of field-programmable analogue array hardware to implement an approximated fractional step transfer function. They compare the experimental results with simulation performed in MATLAB. In order to implement the filters, they approximate the fractional operator $s^{\alpha }$ with integer order transfer function.

Another approach consists of designing non-integer order filters directly in discrete domain. For example, in Stanislawski et al. [37, 38] use Grünwald-Letnikow difference to design discrete filters. Another proposition of non-integer order discrete filter can be found in [13].

Main contribution of this paper is the use of efficient and numerically robust methods for implementation of non-integer order filters. The methods use the state-space formalism allowing easy implementation in the form of both MATLAB/Simulink blocks and direct coding. Methods have different underlying principles which allow covering wider area of filters allowing choice of proper method for appropriate task. Both methods allow very fast sampling frequencies without loss of stability. Methods are illustrated with use of low- pass generalization of classical second-order filter (also known as bi-fractional filter).

Rest of the paper is organized as follows. Firstly, certain preliminaries are presented, containing definitions and properties of necessary elements. This section includes also a brief description of analyzed filter, along with certain results on its stability and general remarks on discrete filter realization. Next, the first of considered methods is presented, the Oustaloup method, and general discussion on its digital implementations is given, including the description of some issues observed during discretization. The next section provides theoretical background for another method used for approximation based on impulse response of analyzed filter. Then, these two methods are compared basing on proposed performance indicator in $\mathcal {H}_{\infty }$ space. As an example of implementation, the results of filtering an EEG signal are presented. Paper ends with conclusions and some propositions on further works.

Remark 1

In this paper, we will use the following notation: Scalars will be marked with lowercase slanted letters (e.g., $\alpha \in \mathbb {R}$); vectors with lowercase bold-upright (e.g., $\mathbf {x}\in \mathbb {R}^n$) and matrices with uppercase bold-upright (e.g., $\mathbf {A}\in \mathbb {R}^{n\times n}$).

2 Preliminaries

This section includes some theoretical preliminaries of the paper. In particular, necessary definitions of non-integer derivatives and function spaces are given.

Also the filter used to illustrate the operation of considered methods is described. Finally, general considerations regarding discrete realization of non-integer order filters are presented.

2.1 Non-integer Order Calculus

There are at least three widely used definitions of non-integer order derivatives [31]. In this paper, we will use the Caputo derivative of order $\alpha$:

$$\begin{aligned} ^C_{0}\mathrm {D}^{\alpha }_tf(x)=\frac{1}{\varGamma (n-\alpha )}\int \limits _0^t\frac{f^{(n)}(\tau )\mathrm {d}\tau }{(t-\tau ^{\alpha +1-n})} \end{aligned}$$

(1)

where $\varGamma (\cdot )$ denotes the gamma function

$$\begin{aligned} \varGamma (t)=\int \limits _0^{\infty }x^{t-1}\mathrm {e}^{-x}\mathrm {d}x. \end{aligned}$$

(2)

Another definition is useful for practical and numerical implementations—Grünwald-Letnikow definition of fractional derivative of order $\alpha$

$$\begin{aligned} {}^{GL}_0\mathrm {D}^{\alpha }_h f(x)=\lim \limits _{h\rightarrow 0}\frac{1}{h^{\alpha }}\sum \limits _{0\le m<\infty }(-1^m){{\alpha }\atopwithdelims (){m}} f(x-mh) \end{aligned}$$

(3)

It should be noted that Caputo and Grünwald-Letnikow derivatives used in non-integer differential equations give the same results only for 0 initial conditions. The third popular definition—Riemann-Liouville—is not used in this paper, and it is, however, equivalent to Grünwald-Letnikov one.

Also we will denote by $\mathcal {L}^1$ the Banach space of absolute integrable functions, and by $\mathcal {L}^2$ the Hilbert space of square integrable functions with scalar product

$$\begin{aligned} \langle x|y\rangle =\int \limits _0^{\infty }x(\theta )y(\theta )\mathrm {d}\theta \end{aligned}$$

(4)

and norm $\Vert x \Vert ^2_2=\langle x|x\rangle$. Additionally, $\mathcal {H}_{\infty }$ will denote Hardy space of bounded holomorphic functions, with the norm

$$\begin{aligned} \Vert x \Vert _\infty =\sup _\omega |x(j\omega )| \end{aligned}$$

(5)

2.2 Non-integer Low-Pass Filter

In their celebrated paper [34], Radwan et al. have presented a non-integer generalization of classical second-order filter section. In this paper, we focus on the low-pass variant (known also as bi-fractional filter). Such filters are a class of non-integer filters fully characterized by three parameters, $\alpha$, $\xi$ and $\omega _0$, and are given by the following transfer function

$$\begin{aligned} G(s)=\frac{\omega _{0}^{2}}{s^{2\alpha }+2\xi \omega _{0}s^{\alpha }+\omega _{0}^{2}} \end{aligned}$$

(6)

Equivalent representation of (6) is the realization in the form of a system of differential equations of order $\alpha$. This system can take form (see [19])

$$\begin{aligned} \begin{aligned} ^C_{0}\mathrm {D}^{\alpha }_t\mathbf {x}(t)={}&\mathbf {A}\mathbf {x}(t)+\mathbf {B}u(t)\\ y(t)={}&\mathbf {C}\mathbf {x}(t) \end{aligned} \end{aligned}$$

(7)

with the following matrices

$$\begin{aligned} \mathbf {A}={}&\begin{bmatrix} 0&\quad 1\\ -\omega _{0}^{2}&\quad -2 \xi \omega _{0} \end{bmatrix}&\mathbf {B}={}&\begin{bmatrix}0\\1\end{bmatrix}&\mathbf {C}={}&\begin{bmatrix} \omega _{0}^{2}&0\end{bmatrix} \end{aligned}$$

(8)

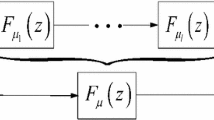
and zero initial conditions $\mathbf {x}(0)=\mathbf {0}\in \mathbb {R}^2$. This system can be realized with non-integer order integrators as in Fig. 1. The conditions for stability of filter (6) are presented in Theorem 1.

Fig. 1

Block diagram realization of (7)

Theorem 1

System in the form (6) or (7)-(8) for $\alpha \in (0,1)$ is asymptotically stable if and only if one of the following conditions holds

• 1. $2\xi \omega _{0}\ge 0$

• 2. $2\xi \omega _{0}<0$ and $\xi >\frac{\tau ^{2}-1}{\tau ^{2}+1}$ where $\tau =\tan \frac{\alpha \pi }{4}$

Proof

Proof can be found in [29]. $\square$

2.3 Discrete Realization of Non-integer Order Filters

In order to implement filters digitally, one needs to take under consideration that non-integer order systems have infinite memory. Their natural discrete realization in the form of Grünwald-Letnikov derivative is not available as it would fill any computer’s memory. Grünwald-Letnikov derivative can be, however, used for filtering of finite length signals, e.g., in post-processing. It can be done using numerical method proposed in [28] based on Grünwald-Letnikov derivative (3) in the following form

$$\begin{aligned} \mathbf {x}(t)={}&(I-h^{\alpha }\mathbf {A})^{-1}\left( h^{\alpha } \mathbf {B}u(t)-\sum _{k=1}^{p}c_{k}\mathbf {x}(t-k h)\right) \end{aligned}$$

(9)

$$\begin{aligned} h={}&T/m,\ t=ph,\ p=0,\ 1,\ \ldots ,\ m \end{aligned}$$

(10)

$$\begin{aligned} c_{k}={}&(-1)^{k} {\alpha \atopwithdelims ()k},\quad k=1,\ 2,\ \ldots ,\ m \end{aligned}$$

(11)

$$\begin{aligned} u_f(t)={}&\mathbf {C x}(t) \end{aligned}$$

(12)

where u(t) is the original signal and $u_f(t)$ is the filtered signal. This direct approach will be used in this paper as a comparison with proposed approximations which are presented in the following sections.

3 Oustaloup Approximation

In this section, we will present well-known Oustaloup approximation, problems with its direct discretization and proposed time-domain realization.

3.1 Continuous Oustaloup Approximation

Continuous Oustaloup filter approximation to a fractional-order differentiator $G(s) = s^{\alpha }$ is widely used in applications [25]. An Oustaloup filter can be designed as

$$\begin{aligned} G(s) = {}&K \prod \limits _{i=1}^{N}\frac{s+\omega '_{i}}{s+\omega _{i}} \end{aligned}$$

(13)

where:

$$\begin{aligned} \begin{aligned} \omega '_{i} ={}&\omega _{b}\omega _{u}^{(2i-1-\alpha )/N}\\ \omega _{i} ={}&\omega _{b}\omega _{u}^{(2i-1+\alpha )/N}\\ K ={}&\omega ^{\alpha }_{h}\\ \omega _{u} ={}&\sqrt{\frac{\omega _{h}}{\omega _{b}}} \end{aligned} \end{aligned}$$

(14)

Approximation is designed for frequencies $\omega \in [\omega _{b},\omega _{h}]$, and N denotes the order of the approximation. As it can be seen, its representation takes form of a product of a series of stable first-order linear systems. As one can observe, choosing a wide band of approximation results in large $\omega _u$ and high-order N results in spacing of poles from close to $-\omega _h$ to those very close to $-\omega _b$. This spacing is logarithmic with a grouping near $-\omega _b$ and causes problems in discretization. Wide band of approximation is desirable, because approximation behaves the best in the interior of the interval and not at its boundary, so certain margins need to be kept.

3.2 Direct Discretization of Transfer Function

In applications, especially when using MATLAB/Simulink environment for real-time control or filtering, two methods of direct implementation of continuous-time systems are established:

• 1. Use them as continuous blocks in Simulink, then use a fixed step explicit solver (e.g., RK4) to evaluate blocks in real time.

• 2. Create discrete transfer functions using some discretization scheme—usually Tustin because it should preserve stability.

The problem with first approach that uses explicit solvers for Oustaloup filters comes from the fastest pole (see [4]) of the transfer function. If the band of approximation is wide, and includes high frequencies, this pole can be located very far to the left of complex plane. It can be observed (see [18]) that Runge–Kutta-type algorithms preserve stability of linear differential equation for such eigenvalues $\lambda$ and discretization step T that stability function of the algorithm $R(T\lambda )$ is less than one. For classical Runge–Kutta algorithm, the stability function is

$$\begin{aligned} R(z)=1+z+\frac{1}{2}z^2+\frac{1}{6}z^3+\frac{1}{24}z^4 \end{aligned}$$

(15)

That means that for $\lambda \in \mathbb {R}$, $T\lambda$ must belong to interval $(-2.785293...,0)$. In considered case and wide bands, the sampling frequency must be at least relatively close to the upper end of the approximation band, which can lead to errors in approximation of frequency characteristics near the Nyquist frequency.

Problems with the second approach come from different reasons. Poles of continuous transfer function have a tendency to group near 0 (especially when lower frequency is small). Those poles will be mapped close to 1 during discretization. In that case, when discretizing every pole separately, denominator of the entire system will include a group of discrete poles similar to $(z-1+\varepsilon _i)(z-1+\varepsilon _{i+1})(z-1+\varepsilon _{i+2})\ldots$ where $\varepsilon _i>0$ are distances of the pole from stability boundary (point $(-1,j0)$ on complex plane) and they are usually very small (orders of magnitude from $10^{-4}$ to $10^{-9}$ are not uncommon). In that case, final denominator will include numbers that will be products of $\varepsilon _i$ with each other, resulting in numbers close to, or below $2.22\cdot 10^{-16}$ which is a smallest number that can be added to another in MATLAB (so-called machine epsilon; in different computation systems, the number is of similar magnitude). It results in rounding error, which high sensitivity of polynomial roots to coefficient values leads to instability. These rounding errors are unavoidable, even when substituting to analytical formulas.

This phenomenon can be observed for example for approximation of order $N=20$. Rounding errors cause Tustin approximation to map real stable poles into complex unstable poles (see Fig. 2).

Fig. 2

Poles of discrete system obtained with Tustin approximation and Oustaloup approximation (in frequency domain) of order 20

3.3 Time-Domain Realization

This method was developed in order to counteract the rounding errors present when discretizing the Oustaloup transfer function.

One can easily observe that for zero initial condition

$$\begin{aligned} \frac{s+\omega '_{k}}{s+\omega _{K}}\iff & {} {\left\{ \begin{array}{ll} \dot{x}_{k} = A_{k} x_{k} +B_{k}u_{k} \\ y_{k} = x_{k} +u_{k} \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} A_{k} = {}&-\omega _{k}, \quad B_{k} = \omega '_{k} - \omega _{k} \end{aligned} \end{aligned}$$

(16)

Because of that (13) can be written in vector matrix notation

$$\begin{aligned} \begin{aligned} \dot{\mathbf {x}} =&{}\begin{bmatrix} A_{1}&\quad 0&\quad 0&\quad \ldots&\quad 0 \\ B_{2}&\quad A_{2}&\quad 0&\quad \ldots&\quad 0 \\ B_{3}&\quad B_{3}&\quad A_{3}&\quad \ldots&\quad 0 \\ \vdots&\quad \vdots&\quad \vdots&\quad \ddots&\quad \vdots \\ B_{N}&\quad B_{N}&\quad \ldots&\quad B_{N}&\quad A_{N} \end{bmatrix} \mathbf {x} + \begin{bmatrix} KB_{1} \\ KB_{2} \\ KB_{3} \\ \vdots \\ KB_{N} \end{bmatrix} u \\ y =&{} \left[ \begin{matrix} 1&1&\ldots&1&1 \end{matrix}\right] \mathbf {x} + Ku \\ \end{aligned} \end{aligned}$$

(17)

or in brief

$$\begin{aligned} \begin{aligned} \dot{\mathbf {x}}={}&\mathbf {Ax}+\mathbf {B}u\\ y={}&\mathbf {Cx}+Du \end{aligned} \end{aligned}$$

(18)

What can be immediately observed is that the matrix $\mathbf {A}$ is triangular. This is extremely important in this problem, as all its eigenvalues (poles of transfer function) are on its diagonal, so there is no need for computing products of eigenvalues, which would lead to rounding errors. Desired property of discretization would be that it should preserve triangular structure, so there would not be any need for eigenvalue multiplication.

3.4 State-Space Discretization

Desired discretization should preserve both traingular structure and stability of the system. Explicit numerical methods generally preserve structure (Euler forward, RK4), but they are still susceptible to problems listed earlier. That is why implicit methods have to be used. In this case, we have used state-space Tustin approximation [15].

Discretized system takes form (for simplicity, e.g., u(Tk) is written as u(k))

$$\begin{aligned} \begin{aligned} \mathbf {{w}}(k+1)={}&{\varvec{\Phi }} \mathbf {w}(k)+\varvec{\Gamma }u(k)\\ y(k)={}&\mathbf {Hw}(k)+Ju(k) \end{aligned} \end{aligned}$$

(19)

where

$$\begin{aligned} \sqrt{T}\mathbf {w}= & {} \left( \mathbf {I}-\mathbf {A}\frac{T}{2}\right) \mathbf {x} -\frac{T}{2}\mathbf {B}u\\ \varvec{\Phi }= & {} \left( \mathbf {I}+\mathbf {A}\frac{T}{2}\right) \left( \mathbf {I}-\mathbf {A}\frac{T}{2}\right) ^{-1}\\ \varvec{\Gamma }= & {} \left( \mathbf {I}-\mathbf {A}\frac{T}{2}\right) ^{-1}\mathbf {B}\sqrt{T}\\ \mathbf {H}= & {} \sqrt{T}\mathbf {C}\left( \mathbf {I}-\mathbf {A}\frac{T}{2}\right) ^{-1}\\ J= & {} D+\mathbf {C}\left( \mathbf {I}-\mathbf {A}\frac{T}{2}\right) ^{-1}\mathbf {B}\frac{T}{2} \end{aligned}$$

As it can be observed, in this case the matrix $\varvec{\Phi }$ is a product of two lower triangular matrices, which preserves structure. Thus, the diagonal consists of discrete system eigenvalues which are discretized individually, so the field for rounding errors is severely reduced. It can be observed that all eigenvalues are in $\mathbb {R}$ and the system is controllable. Also because the method is implicit, the eigenvalues far from imaginary axis are mapped well into unit circle.

Remark 2

It should be noted that Tustin method is implemented in MATLAB c2d function; however, this implementation is not optimized for detecting matrix structure and resulting matrix is not fully triangular (there are nonzero elements with order of magnitude $10^{-12}$ over diagonal). Implementation using efficient matrix inversion algorithms with structure detection solved the problem.

3.5 Filter Realization

The realization of considered filter with use of this variant of Oustaloup method is depicted in Fig. 3. This realization is difficult to analyze, as one has difficulty finding poles of closed-loop system. The closed-loop equivalent system in matrix notation is presented in Lemma 1.

Fig. 3

Realization of filter (6) using discrete time-domain Oustaloup approximation

Lemma 1

Time-domain discrete approximation of filter

$$\begin{aligned} G(s)=\frac{\omega _{0}^{2}}{s^{2\alpha }+2\xi \omega _{0}s^{\alpha }+\omega _{0}^{2}} \end{aligned}$$

(20)

is given by

$$\begin{aligned} \mathbf {z}(k+1)={}&\mathbf {A}_{d}\mathbf {z}(k)+\mathbf {B}_{d}{u}(k) \end{aligned}$$

(21)

$$\begin{aligned} y(k)={}&\mathbf {C}_{d}\mathbf {z}(k)+D_{d}u(k) \end{aligned}$$

(22)

where

$$\begin{aligned} \mathbf {A}_{d}={}&\begin{bmatrix} \varvec{\Phi }-\frac{\omega _0^2 J}{1+2\xi \omega _0J+\omega _0^2J^2}\varvec{\Gamma } \mathbf{H}&\left( 1-J\frac{\omega _0^2J+2\xi \omega _0}{1+2\xi \omega _0J+\omega _0^2J^2}\right) \varvec{\Gamma } \mathbf{H}\\ \frac{-\omega _0^2}{1+2\xi \omega _0J+\omega _0^2J^2}\varvec{\Gamma } \mathbf{H}&\varvec{\Phi }-\frac{\omega _0^2 J+2\xi \omega }{1+2\xi \omega _0J+\omega _0^2J^2}\varvec{\Gamma } \mathbf{H} \end{bmatrix} \end{aligned}$$

(23)

$$\begin{aligned} \mathbf {B}_{d}={}&\begin{bmatrix} \frac{J}{1+2\xi \omega _0J+\omega _0^2J^2}\varvec{\Gamma }\\ \frac{1}{1+2\xi \omega _0J+\omega _0^2J^2}\varvec{\Gamma } \end{bmatrix} \end{aligned}$$

(24)

$$\begin{aligned} \mathbf {C}_{d}={}&\omega _0^2\begin{bmatrix} \left( 1-\frac{\omega _0^2J^2}{1+2\xi \omega _0J+\omega _0^2J^2}\right) \mathbf {H},&J\left( 1-\frac{(\omega _0^2J+2\xi \omega _0)J^2}{1+2\xi \omega _0J+\omega _0^2J}\right) \mathbf {H} \end{bmatrix} \end{aligned}$$

(25)

$$\begin{aligned} D_{d}={}&\frac{\omega _0^2J^2}{1+2\xi \omega _0J+\omega _0^2J^2} \end{aligned}$$

(26)

Proof

The proof is tedious and not very innovative. That is why it is omitted. It requires a solution of a simple set of linear equations and observing which products of vectors result in scalars. $\square$

4 Laguerre Impulse Response Approximation Method

The method of Laguerre impulse response approximation LIRA was introduced by authors in [5]. It should not be confused with traditional discretization method. It is a method for approximating systems given by transfer functions

$$\begin{aligned} \hat{g}(s)=\frac{q_{m}s^{\gamma _m}+q_{m-1}s^{\gamma _{m-1}}+\ldots q_0}{s^{\sigma _n}+p_{n-1}s^{\sigma _{n-1}}+\ldots p_0} \end{aligned}$$

(27)

or more precisely defined by convolution

$$\begin{aligned} y(t)=u*g = \int \limits ^t_0 u(t-\theta )g(\theta )\mathrm {d}\theta \end{aligned}$$

(28)

where $j\le \sigma _j\le j+1$, $j=1,2,\ldots ,n$, $j\le \gamma _j\le j+1$, $j=1,2,\ldots ,m$, $p_j$,$q_j\in \mathbb {R}$. The initial conditions are zero. It is also assumed that $|u(t)|\le u_{max}$ for $t\ge 0$ and $u(t)=0$ for $t<0$ [5]. We assume that $\hat{g}$ is a Laplace transform of a certain function $g:[0,\infty )\rightarrow \mathbb {R}$ which fulfills $g\in \mathcal {L}^1(0,\infty )\cap \mathcal {L}^2(0,\infty )$. This function g is called the impulse response.

It can be shown that the convolution (28) for given input signal u can be approximated with a solution of a system of n linear ordinary differential equations. The approximation uses an orthonormal basis in $\mathcal {L}^2(0,\infty )$

$$\begin{aligned} e_k(\theta ,\mu )=\sqrt{2\mu }e^{-\mu \theta }L_k(2\mu \theta ), \quad k=0,1,2,\ldots \end{aligned}$$

(29)

where $\mu$ is an arbitrary positive constant and $L_k$ is k-th Laguerre polynomial of form

$$\begin{aligned} L_k(z)=\frac{e^z}{k!}\frac{\mathrm {d}^k}{\mathrm {d}z^k}(e^{-z}z^k) \end{aligned}$$

(30)

Theorem 2 gives the conditions that must be fulfilled in order to find the approximation with minimal error.

Theorem 2

If $g\in \mathcal {L}^1(0,\infty )\cap \mathcal {L}^2(0,\infty )$ and $|u(t)|\le u_{max}$ then:

• 1. Response of system defined by convolution (28) can be approximated with

  $$\begin{aligned} y\approx \tilde{y}_n(t) = \sum \limits _{k=0}^{n}\beta _k\xi _k(t) \end{aligned}$$

  (31)

  where set of functions $\xi _k(t):[0,\infty )\rightarrow \mathbb {R}$ is solution of a system of linear differential equations

  $$\begin{aligned} \begin{aligned} \dot{\xi }_k={}&-\mu \xi _k-2\mu \sum \limits _{i=0}^{k-1}\xi _i+\sqrt{2\mu }u\\ \xi _k(0)={}&0, \; k=0, 1, 2,\ldots , n \end{aligned} \end{aligned}$$

  (32)

  and

  $$\begin{aligned} \beta _k = \langle g, e_k(\mu ) \rangle =\int \limits _0^{\infty }g(\theta )e_k(\mu ,\theta )\mathrm {d}\theta \end{aligned}$$

  (33)

• 2. For every $\varepsilon >0$, there exists a number $n_0$ dependent on g, $\varepsilon$ and $u_{max}$ for which approximation error $e_n(t)=x(t)-x_n(t)$ fulfills the inequality

  $$\begin{aligned} |e_n(t)|<\varepsilon \end{aligned}$$

  (34)

  for all $n\ge n_0$ and $t\ge 0$

Proof

For the proof, see [5]. $\square$

The formula (33) for calculating the coefficients is not convenient for numerical implementation as it requires an analytical fomula for impulse response. In [5], the authors presented the following recurrence formula

$$\begin{aligned} \beta _k=\frac{\sqrt{2\mu }}{k!}\sum \limits _{j=0}^{k} {{k}\atopwithdelims (){j}} c_j^k(\mu )\hat{g}^{(k-j)}(\mu ) \end{aligned}$$

(35)

where

$$\begin{aligned} c_j^k=\frac{k-j+1}{2\mu }c_{j-1}^k, \, c_0^k(\mu )=(2\mu )^k, \; j=1,2,\ldots ,k \end{aligned}$$

(36)

and $\hat{g}^{(j)}(s)=\frac{\mathrm {d}^j\hat{g}(s)}{\mathrm {d}s^j}$.

Remark 3

Choice of parameter $\mu$ Method is convergent for any set of orthonormal Laguerre functions, parametrized by $\mu$. However, performance of the method strongly depends on its value, especially for lower orders. In authors’ earlier works, it was shown that $\mu$ chosen by maximization of function:

$$\begin{aligned} J(\mu )= \sum \limits _{k=0}^{n}\beta _k^2(\mu ). \end{aligned}$$

(37)

introduces smallest approximation error in the sense of $\mathcal {L}^2(0,\infty )$. Influence of choosing nonoptimal $\mu$ was investigated in [8, 47].

In summary, the approximation of system defined by convolution (28) can be given in matrix notation as (e.g., for approximation order $n+1$, $\varvec{\upxi }=\begin{bmatrix} \xi _{0}&\xi _{1}&\xi _{2}&\xi _{3}&\xi _{4}&\ldots&\xi _n \end{bmatrix}^\mathsf {T}$):

$$\begin{aligned} \begin{aligned} \dot{\varvec{\upxi }}={}&\begin{bmatrix} -\mu&\quad 0&\quad 0&\quad 0&\quad \ldots&\quad 0\\ -2\mu&\quad -\mu&\quad 0&\quad 0&\quad \ldots&\quad 0\\ -2\mu&\quad -2\mu&\quad -\mu&\quad 0&\quad \ldots&\quad 0\\ -2\mu&\quad -2\mu&\quad -2\mu&\quad -\mu&\quad \ldots&\quad 0\\ \vdots&\quad \vdots&\quad \vdots&\quad \vdots&\quad \ddots&\quad \vdots \\ -2\mu&\quad -2\mu&\quad -2\mu&\quad \ldots&\quad -2\mu&\quad -\mu&\end{bmatrix}\varvec{\upxi }+\begin{bmatrix} \sqrt{2\mu }\\\sqrt{2\mu }\\\sqrt{2\mu }\\\sqrt{2\mu }\\ \vdots \\\sqrt{2\mu } \end{bmatrix}u\\ y={}&\begin{bmatrix} \beta _0&\beta _{1}&\beta _{2}&\beta _{3}&\beta _{4}&\ldots&\beta _{n} \end{bmatrix}\varvec{\upxi } \end{aligned} \end{aligned}$$

(38)

As it can be seen, the state matrix in (38) is also lower triangular. Because of that use of Tustin discretization scheme is reasonable, as it preserves this structure. It should be, however, noted that similarities between time-domain discrete Oustaloup method and LIRA end here.

Instead of approximating the integrators, LIRA method approximates the entire system. As it can be seen in Lemma 1, the closed-loop realization of filter (6) with Oustaloup integrators is quite complicated and closed-loop eigenvalues are not easily available for analysis. In case of LIRA, eigenvalues of filter are not only available, but also state matrix in (38) has n identical eigenvalues and their value can be regulated (moved away from right half plane) and their discrete form is naturally more robust toward rounding errors. It should be also noted that this approximation leads to effective approximation of any order, whereas Oustaloup approximation allows only even values (because two integrators have to be realized).

It should be also noted that explicit discretization schemes can be used, as there are no eigenvalues located farther to the left of imaginary axis than others, which is a natural cause of numerical instability. For further analysis, the same code for obtaining Tustin discretization was used as for the time-domain Oustaloup method.

One weakness of the method is the inability to easily determine the set of filter parameters for which the impulse response of filter fulfills the assumption $g\in \mathcal {L}^1(0,\infty )\cap \mathcal {L}^2(0,\infty )$. Experiments show that assumptions of appropriate integrability are fulfilled if the highest order of denominator of corresponding transfer function is at least 1 / 2 and the transfer function is stable. Fortunately, one can easily observe that the method does not converge for systems not fulfilling that assumption. In Fig. 4, the optimal values of parameter $\mu$ are computed for filter (6) assuming that $\omega _{0}=1$ and other parameters are changed in viable range. In two regions, the convergence was not obtained. First one is the area of unstable pairs $(\xi ,\alpha )$ (see theorem 1), and the other one is located in the area of very low orders $\alpha$. What is interesting is that in the considered range of convergence all $\mu$ are of the same order of magnitude (around 1) and the area boundary is not smooth.

Fig. 4

Choice of $\mu$ maximizing $J(\mu )$ for filter (6) and different values of $\xi$ and $\alpha$ and $\omega _{0}=1$, darker colors indicate the lower values

Other observed weakness of the method is visible for very high orders of approximation (over 20). In that situation, the factorials present in the formulas for $\beta$ coefficients cause numerical errors of rising magnitude. More on that effect is given in [8, 47].

5 Analysis of Filter Behavior

In this section, LIRA and time-domain discrete Oustaloup approximations will be analyzed in order to show merits and flaws of both methods. Whithout loss of generality, analysis is conducted for filter (6) with $\omega _{0}=1$ and varying values of $\xi \in (-1,1)$ and $\alpha \in (0,1)$. Sampling period was chosen as 1ms. For the Oustaloup method, the frequency band was chosen as $[10^{-6}, 10^{3}]$ and in that band the characteristics were compared. For LIRA method parameter, $\mu$ was chosen as maximum of (37) for every case.

The comparison will include:

• analysis of approximation error expressed in the form of $\mathcal {H}_\infty$ norm for wide spectrum of parameters;

• analysis of Bode plots for selected filters;

• filtration of an EEG signal.

Table 1 Comparison of $\mathcal {H}_{\infty }$ norm of approximation error for LIRA and Oustaloup methods with parameters $\xi$ and $\alpha$, and approximation order 6

5.1 $\mathcal {H}_{\infty }$ comparison

This analysis was conducted in order to find an objective criterion for determining the quality of approximation. Because the filter realization is the main concern of this work, $\mathcal {H}_\infty$ norm was chosen as it represents the frequency characteristics. In Tables 1 and 2, the values of approximation error norm $\Vert G(s)-\tilde{G}(s)\Vert _\infty$ are presented for approximation orders of 6 and 12, respectively, for both methods of approximation. $\tilde{G}(s)$ denotes the approximation of filter. The values of $\mathcal {H}_{\infty }$ norm were calculated numerically by computing frequency response of approximations state- space representations in MATLAB (for considered frequency band) and subtracting it from analytically computed frequency response of original filter. Then, maximum of modulus was chosen. In both tables, columns correspond to values of $\alpha$ and rows correspond to $\xi$. For row of $\xi$, there are two sub-rows containing errors of time-domain Oustaloup (marked OT) and LIRA methods. Values of methods with lower error for given $\xi$ and $\alpha$ are marked in bold. Missing values (marked with ’–’) correspond to unstable filters, and zeros represent errors of magnitude less than $10^{-2}$.

Table 2 Comparison of $\mathcal {H}_{\infty }$ norm of approximation error for LIRA and Oustaloup methods with parameters $\xi$ and $\alpha$, and approximation order 12

Careful analysis of data included in Tables 1 and 2 allows drawing the following conclusions:

• 1. For values of $\alpha \ge 0.5$, low-order approximations obtained by LIRA method were either better or at least comparable to those obtained by time-domain Oustaloup method. For higher orders, approximation errors are still comparable.

• 2. For $\alpha <0.5$ LIRA approximations are generally worse, except for some isolated cases. This behavior of LIRA is justified that only for those values of $\alpha$ the impulse responses are believed to be in the required space of $\mathcal {L}^1\cap \mathcal {L}^2$. It should be, however, noted that it was not yet formally proven.

• 3. Generally, for LIRA approximation, errors are decreasing with its order, but convergence (in the sense of $\mathcal {H}_{\infty }$ norm) is slow. Therefore, it can be observed that if approximation is correct it will be correct even for low orders.

• 4. Increasing order of Oustaloup approximation results in more evenly decreasing error for all admissible values of $\alpha$.

Remark 4

It should be noted that behavior described in the above conclusions is consistent for all investigated orders of approximation. We have included only sixth and 12th orders because all the important effects are visible.

5.2 Detailed Analysis of Selected Filters

In this section, we describe in detail frequency responses of selected filters and their approximations. They were chosen to represent significant effects visible in Tables 1 and 2.

The first of the considered examples is the filter with $\alpha =0.7$ and $\xi =0$, i.e.,

$$\begin{aligned} G(s)=\frac{1}{s^{1.4}+1} \end{aligned}$$

(39)

Results of approximation of sixth order for this filter are presented in the Fig. 5. As it can be seen consistently with conclusion of previous section, the LIRA method provides very good approximation, especially in the magnitude aspect. Also phase approximation is consistent for frequencies $\omega <10\omega _0$. In case of the Oustaloup approximation, oscillations in both magnitude and phase characteristics are observed. Substantial differences are especially visible in the phase characteristic for $\omega >\omega _0$.

Fig. 5

Frequency characteristics of approximated discrete filters—order $n=6$, $\alpha =0.7$, $\xi =0$

Approximations of the same filter of 12th order are presented in the Fig. 6. As it can be seen increasing of order in LIRA leads to very similar results. Slight differences are only in the phase characteristic. Increasing order in the Oustaloup method leads to substantial improvement, as the oscillations are strongly reduced and phase characteristic is consistent for $\omega <10\omega _0$.

Fig. 6

Frequency characteristics of approximated discrete filters—order $n=12$, $\alpha =0.7$, $\xi =0$

The second example considers the case of $\alpha <0.5$, in particular filter with parameters $\alpha =0.3$ and $\xi =0.6$, i.e.,

$$\begin{aligned} G(s)=\frac{1}{s^{0.6}+0.6s^{0.3}+1} \end{aligned}$$

(40)

Results of approximation of sixth order for this filter are presented in the Fig. 7. Approximation behavior is, as expected in previous section, in favor of Oustaloup method. Magnitude characteristic is oscillating around the ideal value visibly keeping the trend. Phase characteristic exhibits oscillatory behavior. Approximation obtained with LIRA method is consistent only for frequencies $\omega >10\omega _0$. For lower frequencies, it provides static damping close to 16 dB. Phase characteristic also is significantly different from the desired one.

Fig. 7

Frequency characteristics of approximated discrete filters—order $n=6$, $\alpha =0.3$, $\xi =0.6$

Increase in order to 12th leads to results presented in the Fig. 8. For Oustaloup method, a substantial improvement is observed, especially in the magnitude characteristic, which now very closely follows the characteristic of (40). In case of LIRA, the approximation is essentially unchanged, with static damping of frequencies $\omega <10 \omega _0$ lower by approximately 1 dB.

Fig. 8

Frequency characteristics of approximated discrete filters—order $n=12$, $\alpha =0.3$, $\xi =0.6$

The final considered example is the filter with parameters $\alpha =0.4$ and $\xi =-0.2$, i.e.,

$$\begin{aligned} G(s)=\frac{1}{s^{0.8}-0.4s^{0.4}+1} \end{aligned}$$

(41)

It is one of the mentioned before isolated cases, where for $\alpha <0.5$ the LIRA method provides substantially better low-order approximation than Oustaloup method. It can be observed in Fig. 9. Approximation behavior is very similar to the one characteristic for $\alpha >0.5$. It should be noted that increase in order for Oustaloup method improves the quality of approximation (not presented in detail, but visible in Table 2).

Fig. 9

Frequency characteristics of approximated discrete filters—order $n=6$, $\alpha =0.4$, $\xi =-0.2$

5.3 Example of Filtering

In this section, a brief example of filter behavior in time domain will be presented. A set of EEG data is being considered for analysis of delta waves which are located in the frequencies below 3 Hz. Authors were tasked with providing a non-integer low-pass filter which would introduce slower damping than 40 dB/dec with standard second-order filter [20, 21]. Filter (6) was used with parameters: $\alpha =0.7$, $\xi =0.5$, $\omega _{0}=(6 \pi )^{\alpha }$.

Signals were sampled with frequency of 50 Hz. This filter was originally used in postprocessing with non-integer filtration given by (9)–(12). Here we present it as a comparison with approximated filters. Filter approximations were of sixth order. As one can see in the Fig. 10, the results are qualitatively identical. Analysis of frequency spectrum of filtered and original signals allows to observe the differences between realizations (see Fig. 11). Methods proposed in the paper realize filtering properly offering the expected damping of 28 dB/dec. The numerical method given by (9)–(12) is presenting inferior behavior. Filtration realized in that way introduces unwanted damping for low frequencies, and for frequencies above 3 Hz, the damping is not consistent with expected 28 dB/dec.

Fig. 10

Results of filtering of EEG signal with different filter realizations a with numerical method (9)–(12), b discrete time- domain Oustaloup approximation, c LIRA

Fig. 11

Spectra of filtered original and filtered signals

6 Conclusions and Future Work

In this paper, two efficient methods for digital realization of non-integer order filters were compared. Both these methods have their own merits. Discrete time-domain Oustaloup method allows the approximation of the filter for wider spectrum of parameters than LIRA. However, its coefficients are more numerically sensitive to discretization. Also, the necessity of using two integrators leads to complicated matrices as presented in Lemma 1. Also influence of parameters on the eigenvalues of closed-loop systems is not straightforward. These weaknesses do not appear in LIRA method. The structure of state-space representation is simple, and behavior of $\mu$ is predictable. On the other hand, verification of the assumptions is difficult. Regarding the quality of approximation, there is no clear ’winner’ as the performance strongly depends on the order of approximation and parameters of the system. Impulse response approximation leads to filters with smaller gains for low frequencies. However, for low order of approximation, LIRA is better (or at least comparable) than Oustaloup method. Oustaloup-based method usually works in the desired bandwidth, sometimes with problems on the boundary (see, e.g., Fig. 6).

Future work will focus on the following areas. First of them is the improvement of LIRA method in aspects of assumption verification and numerical errors for approximations of order over 20. The second aspect is the verification if the realization of Oustaloup transfer function is optimal. In authors’ opinion, it is superior to the currently discussed in the literature (one of them has diagonal state matrix, which should be beneficial, but coefficients in the control matrix are very sensitive to rounding errors and another one is a Frobenius matrix realization, which has the same sensitivity as the transfer function). The third considered area is the real-time implementation of the filters. Authors have experience in implementing simple non-integer order filters on embedded platforms and want to develop it further (see, e.g., [14]).