Abstract
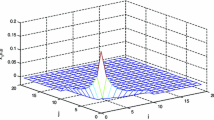
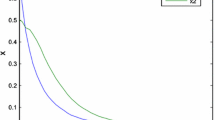
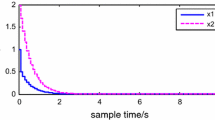
This paper investigates the stability and \(L_1\)-gain control of two-dimensional (2-D) continuous positive switched delayed systems. Firstly, by constructing an appropriate co-positive Lyapunov–Krasovskii functional, a sufficient condition for asymptotical stability of the system under consideration is derived. Secondly, \(L_1\)-gain performance analysis of the underlying system is investigated. Thirdly, a design methodology for state feedback controller is proposed to ensure that the closed-loop system is asymptotically stable with \(L_1\)-gain performance. Finally, an example is provided to show the effectiveness of the proposed method.





Similar content being viewed by others
References
S. Attasi, Systemes Lineaires Homogenes a Deux Indices (IRIA, Rapport, Laboria, 1973)
M. Benhayoun, A. Benzaouia, F. Mesquine, F. Tadeo, Stabilization of 2-D continuous systems with multi-delays and saturated control. in Proceedings of the 18th Mediterranean Conference on Control and Automation (2010), pp. 993-999
M. Benhayoun, F. Mesquine, A. Benzaouia, Delay-dependent stabilizability of 2-D delayed continuous systems with saturating control. Circuits Syst. Signal Process. 32(6), 2723–2743 (2013)
L. Benvenuti, A. Santis, L. Farina, Positive Systems, Lecture Notes in Control and Information Sciences (Springer, Berlin, 2003)
A. Benzaouia, M. Benhayoun, F. Tadeo, State-feedback stabilization of 2-D continuous systems with delays. Int. J. Innov. Comput. Inf. Control 7(2), 977–988 (2011)
A. Benzaouia, A. Hmamed, F. Tadeo, A. Hajjaji, Stabilisation of discrete 2-D time switching systems by state feedback control. Int. J. Syst. Sci. 42(3), 479–487 (2010)
R.N. Bracewell, Two-Dimensional Imaging (Prentice Hall, Upper Saddle River, 1995)
M.S. Branicky, Multiple Lyapunov functions and other analysis tools for switched and hybrid systems. IEEE Trans. Autom. Control 43(4), 475–482 (1998)
S.P. Boyd, L. El Ghaoui, E. Feron, V. Balakrishnan, Linear Matrix Inequalities in System and Control Theory (SIAM, Philadelphia, 1994)
C. Briat, Robust stability and stabilization of uncertain linear positive systems via integral linear constraints: \(L_1\)-gain and \(L_\infty \)-gain characterization. Int. J. Robust Nonlinear Control 23(17), 1932–1954 (2013)
S.F. Chen, Delay-dependent stability for 2-D systems with time-varying delay subject to state saturation in the Roesser model. Appl. Math. Comput. 216(9), 2613–2622 (2010)
X. Chen, J. Lam, P. Li, Z. Shu, \(l_1\)-induced norm and controller synthesis of positive systems. Automatica 49(5), 1377–1385 (2013)
S. Dashkovskiy, L. Naujok, Lyapunov–Razumikhin and Lyapunov–Krasovskii theorems for interconnected ISS time-delay systems. in Proceedings of the 19th International Symposium on Mathematical Theory of Networks and Systems (2010), pp. 5–9
C. Du, L. Xie, \(H_{\infty }\) Control and Filtering of Two-Dimensional Systems (Springer, Berlin, 2002)
Z. Duan, Z. Xiang, \(H_2\) output feedback controller design for discrete-time 2D switched systems. Trans. Inst. Meas. Control 36(1), 68–77 (2014)
Z. Duan, Z. Xiang, H.R. Karimi, Delay-dependent exponential stabilization of positive 2-D switched state-delayed systems in the Roesser model. Inf. Sci. 272, 173–184 (2014)
C. El-Kasri, A. Hmamed, E.H. Tissir, F. Tadeo, Robust \(H_\infty \) filtering for uncertain two-dimensional continuous systems with time-varying delays. Multidimens. Syst. Sign. Process. 24(4), 685–706 (2013)
K. Fernando, Stability of 2-D State Space Systems (NAG Technical Report TR4/88, 1988)
E. Fornasini, G. Marchesini, Doubly-indexed dynamical systems, state-space models and structural properties. Math. Syst. Theory 12(1), 59–72 (1978)
E. Fridman, S.I. Niculescu, On complete Lyapunov–Krasovskii functional techniques for uncertain systems with fast-varying delays. Int. J. Robust Nonlinear Control 18(3), 364–374 (2008)
P. Gahinet, A. Nemirovskii, A.J. Laub, M. Chilali, The LMI control toolbox. in IEEE Conference on Decision and Control (1994), pp. 2038-2038
M. Ghamgui, N. Yeganefar, O. Bachelier, D. Mehdi, Exponential stability conditions for 2-D continuous state-delayed systems. in 7th International Workshop on Multidimensional (nD) Systems (nDs) (2011), pp. 1–5
I. Ghous, Z. Xiang, Robust state feedback \(H_\infty \) control for uncertain 2-D continuous state delayed systems in the Roesser model. Multidimens. Syst. Sign. Process. (2014). doi:10.1007/s11045-014-0301-8
I. Ghous, Z. Xiang, \(H_\infty \) stabilization of 2-D discrete switched delayed systems represented by the Roesser model subject to actuator saturation. Trans. Inst. Meas. Control (2014). doi:10.1177/0142331214560805
I. Ghous, Z. Xiang, H.R. Karimi, State feedback \(H_\infty \) control for 2-D switched delay systems with actuator saturation in the second FM model. Circuits Syst. Signal Process. 34(7), 2167–2192 (2015)
A. Hmamed, M. Alfidi, A. Benzaouia, F. Tadeo, LMI conditions for robust stability of 2-D linear discrete-time systems. Math. Probl. Eng. 2008, 356124 (2008). doi:10.1155/2008/356124
A. Hmamed, F. Mesquine, F. Tadeo, M. Benhayoun, A. Benzaouia, Stabilization of 2-D saturated systems by state feedback control. Multidimens. Syst. Sign. Process. 21(3), 277–292 (2010)
S. Huang, Z. Xiang, Delay-dependent stability for discrete 2-D switched systems with state delays in the Roesser model. Circuits Syst. Signal Process. 32(6), 2821–2837 (2013)
A. Jadbabaie, J. Lin, A.S. Morse, Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 48(6), 988–1001 (2003)
T. Kaczorek, Two-Dimensional Linear Systems (Springer, Berlin, 1985)
T. Kaczorek, Positive 1D and 2D Systems (Springer, London, 2002)
T. Kaczorek, A realization problem for positive continuous-time systems with reduced numbers of delays. Int. J. Appl. Math. Comput. Sci 16(3), 325–331 (2006)
T. Kaczorek, The choice of the forms of Lyapunov functions for a positive 2-D Roesser model. Int. J. Appl. Math. Comput. Sci 17(4), 471–475 (2007)
T. Kaczorek, Asymptotic stability of positive 2-D linear systems with delays. Bull. Pol. Acad. Sci. Tech. Sci 57(2), 133–138 (2009)
T. Kaczorek, LMI approach to stability of 2-D positive systems. Multidimens. Syst. Sign. Process. 20(1), 39–54 (2009)
T. Kaczorek, Practical stability and asymptotic stability of positive fractional 2-D linear systems. Asian J. Control 12(2), 200–207 (2010)
V.L. Kharitonov, Robust stability analysis of time delay systems: a survey. Annu. Rev. Control 23, 185–196 (1999)
D. Liberzon, A.S. Morse, Basic problems in stability and design of switched systems. IEEE Control Syst. 19(5), 59–70 (1999)
H. Lin, P.J. Antsaklis, Stability and stabilizability of switched linear systems: a survey of recent results. IEEE Trans. Autom. Control 54(2), 308–322 (2009)
S. Liu, Z. Xiang, Exponential \(L_1\) output tracking control for positive switched linear systems with time-varying delays. Nonlinear Anal. Hybrid Syst. 11, 118–128 (2014)
O. Mason, R. Shorten, On linear copositive Lyapunov functions and the stability of switched positive linear systems. IEEE Trans. Autom. Control 52(7), 1346–1349 (2007)
A. Papachristodoulou, M. Peet, S. Lall, Constructing Lyapunov–Krasovskii functionals for linear time delay systems. in Proceedings of the American Control Conference (2005), pp. 2845–2850
W. Paszke, J. Lam, K. Gałkowski, S. Xu, Z. Lin, Robust stability and stabilisation of 2-D discrete state-delayed systems. Syst. Control Lett. 51(3–4), 277–291 (2004)
R.P. Roesser, A discrete state-space model for linear image processing. IEEE Trans. Autom. Control 20(1), 1–10 (1975)
R. Shorten, K. Narendra, On the stability and existence of common Lyapunov functions for stable linear switching systems. in Proceedings of the 37th IEEE Conference on Decision and Control (1998), pp. 3723–3724
R. Shorten, F. Wirth, D. Leith, A positive systems model of TCP-like congestion control: asymptotic results. IEEE/ACM Trans. Netw. 14(3), 616–629 (2006)
H.R. Shaker, F. Shaker, Lyapunov stability for continuous-time multidimensional nonlinear systems. Nonlinear Dyn. 75(4), 717–724 (2014)
X. Su, L. Wu, P. Shi, C.P. Chen, Model approximation for fuzzy switched systems with stochastic perturbation. IEEE Trans. Fuzzy Syst. (2014). doi:10.1109/TFUZZ.2014.2362153
X. Su, L. Wu, P. Shi, Y.D. Song, A novel approach to output feedback control of fuzzy stochastic systems. Automatica 50(12), 3268–3275 (2014)
Y. Tong, C. Wang, L. Zhang, Stabilisation of discrete-time switched positive linear systems via time-and state-dependent switching laws. IET Control Theory Appl. 6(11), 1603–1609 (2012)
M. Xiang, Z. Xiang, Stability, \(L_1\)-gain and control synthesis for positive switched systems with time-varying delay. Nonlinear Anal. Hybrid Syst. 9(1), 9–17 (2013)
R. Yang, G.P. Liu, P. Shi, C. Thomas, M.V. Basin, Predictive output feedback control for networked control systems. IEEE Trans. Ind. Electron. 61(1), 512–520 (2014)
Acknowledgments
This work was supported by the National Natural Science Foundation of China under Grant No. 61273120 and the Postgraduate Innovation Project of Jiangsu Province (Grant No. KYLX_378).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ghous, I., Huang, S. & Xiang, Z. State Feedback \(L_1\)-Gain Control of Positive 2-D Continuous Switched Delayed Systems Via State-Dependent Switching. Circuits Syst Signal Process 35, 2432–2449 (2016). https://doi.org/10.1007/s00034-015-0161-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-015-0161-y