Skip to main content
SpringerLink
Log in

Scattering of SH waves by lined tunnel in inhomogeneous right-angle space with variable shear modulus

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

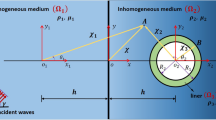
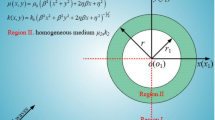
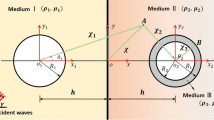
Based on the theory of complex function, the seismic response of tunnel structure in inhomogeneous elastic right-angle space under different stiffness is solved. The inhomogeneous form of shear modulus is used to reflect the variation regular of stiffness. The governing equations are obtained by means of displacement auxiliary function and mapping function. At the same time, the calculation model is established by means of the image method, and the series solution of the wave field is constructed and mainly analyses the distribution of displacement amplitude on the surface and dynamic stress concentration factor on the lining.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Panji, M., Ansari, B.: Transient SH-wave scattering by the lined tunnels embedded in an elastic half-plane. Eng. Anal. Bound. Elem. 84, 220–230 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  2. Esmaeili, M., Vahdani, S., Noorzad, A.: Dynamic response of lined circular tunnel to plane harmonic waves. Tunn. Undergr. Space Technol. 21, 511–519 (2006)

    Article  Google Scholar 

  3. Liu, Z.X., Liu, J.Q., Pei, Q., Yu, H.T., Li, C.C., Wu, C.Q.: Seismic response of tunnel near fault fracture zone under incident SV waves. Undergr. Space 6, 695–708 (2021)

    Article  Google Scholar 

  4. Fu, J., Liang, J.W., Qin, L.: Dynamic soil-tunnel interaction in layered half-space for incident plane SH waves. Earthq. Eng. Eng. Vib. 15, 715–727 (2016)

    Article  Google Scholar 

  5. Rashiddel, A., Koopialipoor, M., Hadei, M.R., Rahmannejad, R.: Numerical investigation of closed-form solutions for seismic design of a circular tunnel lining (by quasi-static method). Civ. Eng. J. Tehran 4, 239–257 (2018)

    Article  Google Scholar 

  6. Xu, H., Li, T.B., Xu, J.S., Wang, Y.J.: Dynamic response of underground circular lining tunnels subjected to incident P waves. Math. Probl. Eng. 2014, 297424 (2014)

    Article  MathSciNet  Google Scholar 

  7. Jin, L.G., Sun, H.Y., Wang, S.N., Zhou, Z.H.: A series solution for 2D scattering of cylindrical sh-waves by surrounding loose rock zone of underground tunnel lining. Front. Phys. 9, 772823 (2021)

    Article  Google Scholar 

  8. Akhlaghi, T., Nikkar, A.: Effect of vertically propagating shear waves on seismic behavior of circular tunnels. Sci. World J. 806092 (2014)

  9. Lyu, D., Ma, S., Yu, C., Liu, C.C., Wang, X.W., Yang, B.Y., Xiao, M.: Effects of oblique incidence of SV waves on nonlinear seismic response of a lined arched tunnel. Shock. Vib. 2020, 8093804 (2020)

    Google Scholar 

  10. Huang, J.Q., Du, X.L., Zhao, M., Zhao, X.: Impact of incident angles of earthquake shear (S) waves on 3-D non-linear seismic responses of long lined tunnels. Eng. Geol. 222, 168–185 (2017)

    Article  Google Scholar 

  11. Bouare, H., Mesgouez, A., Lefeuve-Mesgouez, G.: Stress and displacement fields around an arbitrary shape tunnel surrounded by a multilayered elastic medium subjected to harmonic waves under plane strain conditions. Soil Dyn. Earthq. Eng. 154, 107158 (2022)

    Article  Google Scholar 

  12. Pelli, E., Sofianos, A.I.: Analytical calculation of the half space stress field around tunnels under seismic loading of SV waves. Tunn. Undergr. Space Technol. 79, 150–174 (2018)

    Article  Google Scholar 

  13. Zhao, W.S., Chen, W.Z., Yang, D.S.: Interaction between strengthening and isolation layers for tunnels in rock subjected to SH waves. Tunn. Undergr. Space Technol. 79, 121–133 (2018)

    Article  Google Scholar 

  14. Kara, H.F.: A note on response of tunnels to incident SH-waves near hillsides. Soil Dyn. Earthq. Eng. 90, 138–146 (2016)

    Article  Google Scholar 

  15. Qi, H., Zhang, Y., Guo, J., Chu, F.Q.: Dynamic stress analysis of a circular-lined tunnel in composite strata-SH wave incidence. Adv. Civ. Eng. 2020, 8827737 (2020)

    Google Scholar 

  16. Deliktas-Ozdemir, E., Ahmetolan, S., Tuna, D.: Existence of solitary SH waves in a heterogeneous elastic two-layered plate. Z. Angew. Math. Phys. 73(6), 1–17 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  17. Deliktas-Ozdemir, E., Teymur, M.: Nonlinear surface SH waves in a half-space covered by an irregular layer. Z. Angew. Math. Phys. 73, 145 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  18. Filshtinsky, M.L., Nardzokas, D.I.: The shear wave diffraction on tunnel cavities in an elastic layer and a half-layer. Arch. Appl. Mech. 71, 341–352 (2001)

    Article  MATH  Google Scholar 

  19. Sanchez-Merino, A.L., Fernandez-Saez, J., Navarro, C.: Simplified longitudinal seismic response of tunnels linings subjected to surface waves. Soil Dyn. Earthq. Eng. 29, 579–582 (2009)

    Article  Google Scholar 

  20. Kung, C.L., Wang, T.T., Chen, C.H., Huang, T.H.: Response of a circular tunnel through rock to a harmonic rayleigh wave. Rock Mech. Rock Eng. 51, 547–559 (2018)

    Article  Google Scholar 

  21. Zhao, W.S., Chen, W.Z., Yang, D.S., Gao, H., Xie, P.Y.: Analytical solution for seismic response of tunnels with composite linings in elastic ground subjected to Rayleigh waves. Soil Dyn. Earthq. Eng. 153, 107113 (2022)

    Article  Google Scholar 

  22. Watanabe, K., Nishinari, K.: SH-wave in a cylindrically anisotropic solid. Z. Angew. Math. Phys. 47(6), 906–914 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  23. Ilyashenko, A., Kuznetsov, S.: SH waves in anisotropic (monoclinic) media. Z. Angew. Math. Phys. 69(1), 17 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  24. Liu, D.K., Gai, B.Z., Tao, G.Y.: Applications of the method of complex functions to dynamic stress concentrations. Wave Motion 4, 293–304 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  25. Mow, C.C., Pao, Y.H.: “The Diffraction of Elastic Waves and Dynamic Stress Concentrations” Rand Corp (1971)

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 12072085) and the Natural Science Foundation of Heilongjiang Province of China (No. ZD2021A001) and Research Team Project of Heilongjiang Natural Science Foundation (No. TD2020A001) and the program for Innovative Research Team in China Earthquake Administration.

Author information

Authors and Affiliations

  1. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin, 150001, China

    Jin-lai Bian, Zai-lin Yang, Yong Yang & Meng-han Sun

  2. Key Laboratory of Advanced Material of Ship and Mechanics, Ministry of Industry and Information Technology, Harbin Engineering University, Harbin, China

    Zai-lin Yang, Yong Yang & Meng-han Sun

Authors
  1. Jin-lai Bian
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zai-lin Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Meng-han Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Each author contributed to this paper. JL-B and ZL-Y wrote this paper, YY and MH-S analyzed the results, JL-B and YY processed the data, and ZL-Y provided methodological guidance.

Corresponding author

Correspondence to Meng-han Sun.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

Stress expressions for incident and reflected waves

$$\begin{aligned}{} & {} \begin{array}{l} \tau _{rz}^{1\text{ i }} =-\frac{\mu _{0} \varphi _{0} \beta }{2\sqrt{\left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) } }\exp \left( {\frac{ik_{t} }{2}\left( {\zeta \text{ e}^{-i\alpha }+\bar{{\zeta }}\text{ e}^{i\alpha }} \right) } \right) \\ \left[ {\left( {\beta \bar{{Z}}+\eta } \right) \left( {1-ik_{t} \text{ e}^{-i\alpha }} \right) \text{ e}^{i\theta }+\left( {\beta Z+\eta } \right) \left( {1-ik_{t} \text{ e}^{i\alpha }} \right) \text{ e}^{-i\theta }} \right] \\ \end{array} \end{aligned}$$
(A.1)
$$\begin{aligned}{} & {} \begin{array}{l} \tau _{\theta z}^{1\text{ i }} =-\frac{i\mu _{0} \varphi _{0} \beta }{2\sqrt{\left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) } }\exp \left( {\frac{ik_{t} }{2}\left( {\zeta \text{ e}^{-i\alpha }+\bar{{\zeta }}\text{ e}^{i\alpha }} \right) } \right) \\ \left[ {\left( {\beta \bar{{Z}}+\eta } \right) \left( {1-ik_{t} \text{ e}^{-i\alpha }} \right) \text{ e}^{i\theta }-\left( {\beta Z+\eta } \right) \left( {1-ik_{t} \text{ e}^{i\alpha }} \right) \text{ e}^{-i\theta }} \right] \\ \end{array} \end{aligned}$$
(A.2)
$$\begin{aligned}{} & {} \begin{array}{l} \tau _{rz}^{2\text{ r }} =-\frac{\mu _{0} \varphi _{0} \beta }{2\sqrt{\left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) } }\exp \left( {\frac{ik_{t} }{2}\left( {\zeta \text{ e}^{i\alpha }+\bar{{\zeta }}\text{ e}^{-i\alpha }} \right) } \right) \\ \left[ {\left( {\beta \bar{{Z}}+\eta } \right) \left( {1-ik_{t} \text{ e}^{i\alpha }} \right) \text{ e}^{i\theta }+\left( {\beta Z+\eta } \right) \left( {1-ik_{t} \text{ e}^{-i\alpha }} \right) \text{ e}^{-i\theta }} \right] \\ \end{array} \end{aligned}$$
(A.3)
$$\begin{aligned}{} & {} \begin{array}{l} \tau _{\theta z}^{2\text{ r }} =-\frac{i\mu _{0} \varphi _{0} \beta }{2\sqrt{\left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) } }\exp \left( {\frac{ik_{t} }{2}\left( {\zeta \text{ e}^{i\alpha }+\bar{{\zeta }}\text{ e}^{-i\alpha }} \right) } \right) \\ \left[ {\left( {\beta \bar{{Z}}+\eta } \right) \left( {1-ik_{t} \text{ e}^{i\alpha }} \right) \text{ e}^{i\theta }-\left( {\beta Z+\eta } \right) \left( {1-ik_{t} \text{ e}^{-i\alpha }} \right) \text{ e}^{-i\theta }} \right] \\ \end{array} \end{aligned}$$
(A.4)
$$\begin{aligned}{} & {} \begin{array}{l} \tau _{rz}^{3\text{ r }} =-\frac{\mu _{0} \varphi _{0} \beta }{2\sqrt{\left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) } }\exp \left( {-\frac{ik_{t} }{2}\left( {\zeta \text{ e}^{-i\alpha }+\bar{{\zeta }}\text{ e}^{i\alpha }} \right) } \right) \\ \left[ {\left( {\beta \bar{{Z}}+\eta } \right) \left( {1+ik_{t} \text{ e}^{-i\alpha }} \right) \text{ e}^{i\theta }+\left( {\beta Z+\eta } \right) \left( {1+ik_{t} \text{ e}^{i\alpha }} \right) \text{ e}^{-i\theta }} \right] \\ \end{array} \end{aligned}$$
(A.5)
$$\begin{aligned}{} & {} \begin{array}{l} \tau _{\theta z}^{3\text{ r }} =-\frac{i\mu _{0} \varphi _{0} \beta }{2\sqrt{\left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) } }\exp \left( {-\frac{ik_{t} }{2}\left( {\zeta \text{ e}^{-i\alpha }+\bar{{\zeta }}\text{ e}^{i\alpha }} \right) } \right) \\ \left[ {\left( {\beta \bar{{Z}}+\eta } \right) \left( {1+ik_{t} \text{ e}^{-i\alpha }} \right) \text{ e}^{i\theta }-\left( {\beta Z+\eta } \right) \left( {1+ik_{t} \text{ e}^{i\alpha }} \right) \text{ e}^{-i\theta }} \right] \\ \end{array} \end{aligned}$$
(A.6)
$$\begin{aligned}{} & {} \begin{array}{l} \tau _{rz}^{4\text{ r }} =-\frac{\mu _{0} \varphi _{0} \beta }{2\sqrt{\left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) } }\exp \left( {-\frac{ik_{t} }{2}\left( {\zeta \text{ e}^{i\alpha }+\bar{{\zeta }}\text{ e}^{-i\alpha }} \right) } \right) \\ \left[ {\left( {\beta \bar{{Z}}+\eta } \right) \left( {1+ik_{t} \text{ e}^{i\alpha }} \right) \text{ e}^{i\theta }+\left( {\beta Z+\eta } \right) \left( {1+ik_{t} \text{ e}^{-i\alpha }} \right) \text{ e}^{-i\theta }} \right] \\ \end{array} \end{aligned}$$
(A.7)
$$\begin{aligned}{} & {} \begin{array}{l} \tau _{\theta z}^{4\text{ r }} =-\frac{i\mu _{0} \varphi _{0} \beta }{2\sqrt{\left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) } }\exp \left( {-\frac{ik_{t} }{2}\left( {\zeta \text{ e}^{i\alpha }+\bar{{\zeta }}\text{ e}^{-i\alpha }} \right) } \right) \\ \left[ {\left( {\beta \bar{{Z}}+\eta } \right) \left( {1+ik_{t} \text{ e}^{i\alpha }} \right) \text{ e}^{i\theta }-\left( {\beta Z+\eta } \right) \left( {1+ik_{t} \text{ e}^{-i\alpha }} \right) \text{ e}^{-i\theta }} \right] \\ \end{array} \end{aligned}$$
(A.8)

Scattering waves generated by outer boundary

$$\begin{aligned}{} & {} \begin{array}{l} \tau _{rz}^{\text{ s }} =\frac{\mu _{0} }{\sqrt{\left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) } }\sum \limits _{n=-\infty }^{n=+\infty } {A_{n} } \\ \left[ {\left( {\begin{array}{l} \left( {\frac{\partial S_{n}^{\left( 1 \right) } }{\partial Z_{1} }+\frac{\partial S_{n}^{\left( 2 \right) } }{\partial Z_{1} }+\frac{\partial S_{n}^{\left( 3 \right) } }{\partial Z_{1} }+\frac{\partial S_{n}^{\left( 4 \right) } }{\partial Z_{1} }} \right) \left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) \\ -\frac{1}{2}\beta \left( {\beta \bar{{Z}}+\eta } \right) \left( {S_{n}^{\left( 1 \right) } +S_{n}^{\left( 2 \right) } +S_{n}^{\left( 3 \right) } +S_{n}^{\left( 4 \right) } } \right) \\ \end{array}} \right) } \right. \text{ e}^{i\theta }+ \\ \left. {\left( {\begin{array}{l} \left( {\frac{\partial S_{n}^{\left( 1 \right) } }{\partial \bar{{Z}}_{1} }+\frac{\partial S_{n}^{\left( 2 \right) } }{\partial \bar{{Z}}_{1} }+\frac{\partial S_{n}^{\left( 3 \right) } }{\partial \bar{{Z}}_{1} }+\frac{\partial S_{n}^{\left( 4 \right) } }{\partial \bar{{Z}}_{1} }} \right) \left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) \\ -\frac{1}{2}\beta \left( {\beta Z+\eta } \right) \left( {S_{n}^{\left( 1 \right) } +S_{n}^{\left( 2 \right) } +S_{n}^{\left( 3 \right) } +S_{n}^{\left( 4 \right) } } \right) \\ \end{array}} \right) \text{ e}^{-i\theta }} \right] \\ \end{array} \end{aligned}$$
(A.9)
$$\begin{aligned}{} & {} \begin{array}{l} \tau _{\theta z}^{\text{ s }} =\frac{i\mu _{0} }{\sqrt{\left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) } }\sum \limits _{n=-\infty }^{n=+\infty } {A_{n} } \\ \left[ {\left( {\begin{array}{l} \left( {\frac{\partial S_{n}^{\left( 1 \right) } }{\partial Z_{1} }+\frac{\partial S_{n}^{\left( 2 \right) } }{\partial Z_{1} }+\frac{\partial S_{n}^{\left( 3 \right) } }{\partial Z_{1} }+\frac{\partial S_{n}^{\left( 4 \right) } }{\partial Z_{1} }} \right) \left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) \\ -\frac{1}{2}\beta \left( {\beta \bar{{Z}}+\eta } \right) \left( {S_{n}^{\left( 1 \right) } +S_{n}^{\left( 2 \right) } +S_{n}^{\left( 3 \right) } +S_{n}^{\left( 4 \right) } } \right) \\ \end{array}} \right) } \right. \text{ e}^{i\theta }- \\ \left. {\left( {\begin{array}{l} \left( {\frac{\partial S_{n}^{\left( 1 \right) } }{\partial \bar{{Z}}_{1} }+\frac{\partial S_{n}^{\left( 2 \right) } }{\partial \bar{{Z}}_{1} }+\frac{\partial S_{n}^{\left( 3 \right) } }{\partial \bar{{Z}}_{1} }+\frac{\partial S_{n}^{\left( 4 \right) } }{\partial \bar{{Z}}_{1} }} \right) \left( {\beta Z+\eta } \right) \left( {\beta \bar{{Z}}+\eta } \right) \\ -\frac{1}{2}\beta \left( {\beta Z+\eta } \right) \left( {S_{n}^{\left( 1 \right) } +S_{n}^{\left( 2 \right) } +S_{n}^{\left( 3 \right) } +S_{n}^{\left( 4 \right) } } \right) \\ \end{array}} \right) \text{ e}^{-i\theta }} \right] \\ \end{array} \end{aligned}$$
(A.10)

where

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {\frac{\partial S_{n}^{\left( 1 \right) } }{\partial Z_{1} }=\frac{\beta k_{t} }{2\left( {\beta Z_{1} +\eta } \right) }H_{n-1}^{\left( 1 \right) } \left( {k_{t} \left| {\zeta _{1} } \right| } \right) \left( {\frac{\zeta _{1} }{\left| {\zeta _{1} } \right| }} \right) ^{n-1}} \\ {\frac{\partial S_{n}^{\left( 2 \right) } }{\partial Z_{1} }=-\frac{\beta k_{t} }{2\left( {\beta Z_{2} +\eta } \right) }H_{n+1}^{\left( 1 \right) } \left( {k_{t} \left| {\zeta _{2} } \right| } \right) \left( {\frac{\zeta _{2} }{\left| {\zeta _{2} } \right| }} \right) ^{-n-1}} \\ {\frac{\partial S_{n}^{\left( 3 \right) } }{\partial Z_{1} }=\left( {-1} \right) ^{n}\frac{\beta k_{t} }{2\left( {\beta Z_{3} +\eta } \right) }H_{n-1}^{\left( 1 \right) } \left( {k_{t} \left| {\zeta _{3} } \right| } \right) \left( {\frac{\zeta _{3} }{\left| {\zeta _{3} } \right| }} \right) ^{-n-1}} \\ {\frac{\partial S_{n}^{\left( 4 \right) } }{\partial Z_{1} }=\left( {-1} \right) ^{n+1}\frac{\beta k_{t} }{2\left( {\beta Z_{4} +\eta } \right) }H_{n+1}^{\left( 1 \right) } \left( {k_{t} \left| {\zeta _{4} } \right| } \right) \left( {\frac{\zeta _{4} }{\left| {\zeta _{4} } \right| }} \right) ^{-n-1}} \\ \end{array} }} &{} {{\begin{array}{*{20}c} {\frac{\partial S_{n}^{\left( 1 \right) } }{\partial \bar{{Z}}_{1} }=-\frac{\beta k_{t} }{2\left( {\beta \bar{{Z}}_{1} +\eta } \right) }H_{n+1}^{\left( 1 \right) } \left( {k_{t} \left| {\zeta _{1} } \right| } \right) \left( {\frac{\zeta _{1} }{\left| {\zeta _{1} } \right| }} \right) ^{n+1}} \\ {\frac{\partial S_{n}^{\left( 2 \right) } }{\partial \bar{{Z}}_{1} }=\frac{\beta k_{t} }{2\left( {\beta \bar{{Z}}_{2} +\eta } \right) }H_{n-1}^{\left( 1 \right) } \left( {k_{t} \left| {\zeta _{2} } \right| } \right) \left( {\frac{\zeta _{2} }{\left| {\zeta _{2} } \right| }} \right) ^{-n+1}} \\ {\frac{\partial S_{n}^{\left( 3 \right) } }{\partial \bar{{Z}}_{1} }=\left( {-1} \right) ^{n+1}\frac{\beta k_{t} }{2\left( {\beta \bar{{Z}}_{3} +\eta } \right) }H_{n+1}^{\left( 1 \right) } \left( {k_{t} \left| {\zeta _{3} } \right| } \right) \left( {\frac{\zeta _{3} }{\left| {\zeta _{3} } \right| }} \right) ^{n+1}} \\ {\frac{\partial S_{n}^{\left( 4 \right) } }{\partial \bar{{Z}}_{1} }=\left( {-1} \right) ^{n}\frac{\beta k_{t} }{2\left( {\beta \bar{{Z}}_{4} +\eta } \right) }H_{n-1}^{\left( 1 \right) } \left( {k_{t} \left| {\zeta _{4} } \right| } \right) \left( {\frac{\zeta _{4} }{\left| {\zeta _{4} } \right| }} \right) ^{-n+1}} \\ \end{array} }} \\ \end{array} }} \right. \end{aligned}$$

Refraction waves generated by outer boundary

$$\begin{aligned} \tau _{rz}^{\text{ f }}= & {} \frac{\mu _{2} k_{2} }{2}\sum \limits _{n=-\infty }^{n=+\infty } {B_{n} \left[ {H_{n-1}^{\left( 2 \right) } \left( {k_{2} \left| {Z_{1} } \right| } \right) \left( {\frac{Z_{1} }{\left| {Z_{1} } \right| }} \right) ^{n-1}\text{ e}^{i\theta }-H_{n+1}^{\left( 2 \right) } \left( {k_{2} \left| {Z_{1} } \right| } \right) \left( {\frac{Z_{1} }{\left| {Z_{1} } \right| }} \right) ^{n+1}\text{ e}^{-i\theta }} \right] } \end{aligned}$$
(A.11)
$$\begin{aligned} \tau _{\theta z}^{\text{ f }}= & {} \frac{i\mu _{2} k_{2} }{2}\sum \limits _{n=-\infty }^{n=+\infty } {B_{n} \left[ {H_{n-1}^{\left( 2 \right) } \left( {k_{2} \left| {Z_{1} } \right| } \right) \left( {\frac{Z_{1} }{\left| {Z_{1} } \right| }} \right) ^{n-1}\text{ e}^{i\theta }+H_{n+1}^{\left( 2 \right) } \left( {k_{2} \left| {Z_{1} } \right| } \right) \left( {\frac{Z_{1} }{\left| {Z_{1} } \right| }} \right) ^{n+1}\text{ e}^{-i\theta }} \right] } \end{aligned}$$
(A.12)

Scattering waves generated by inner boundary

$$\begin{aligned} \tau _{rz}^{\text{ s}_{r_{c} } }= & {} \frac{\mu _{2} k_{2} }{2}\sum \limits _{n=-\infty }^{n=+\infty } {C_{n} \left[ {H_{n-1}^{\left( 1 \right) } \left( {k_{2} \left| {Z_{c} } \right| } \right) \left( {\frac{Z_{c} }{\left| {Z_{c} } \right| }} \right) ^{n-1}\text{ e}^{i\theta }-H_{n+1}^{\left( 1 \right) } \left( {k_{2} \left| {Z_{c} } \right| } \right) \left( {\frac{Z_{c} }{\left| {Z_{c} } \right| }} \right) ^{n+1}\text{ e}^{-i\theta }} \right] } \end{aligned}$$
(A.13)
$$\begin{aligned} \tau _{\theta z}^{\text{ s}_{r_{c} } }= & {} \frac{i\mu _{2} k_{2} }{2}\sum \limits _{n=-\infty }^{n=+\infty } {C_{n} \left[ {H_{n-1}^{\left( 1 \right) } \left( {k_{2} \left| {Z_{c} } \right| } \right) \left( {\frac{Z_{c} }{\left| {Z_{c} } \right| }} \right) ^{n-1}\text{ e}^{i\theta }+H_{n+1}^{\left( 1 \right) } \left( {k_{2} \left| {Z_{c} } \right| } \right) \left( {\frac{Z_{c} }{\left| {Z_{c} } \right| }} \right) ^{n+1}\text{ e}^{-i\theta }} \right] } \end{aligned}$$
(A.14)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bian, Jl., Yang, Zl., Yang, Y. et al. Scattering of SH waves by lined tunnel in inhomogeneous right-angle space with variable shear modulus. Z. Angew. Math. Phys. 74, 161 (2023). https://doi.org/10.1007/s00033-023-02047-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-023-02047-0

Keywords

Mathematics Subject Classification

Search

Navigation