Skip to main content
SpringerLink
Log in

Convergence analysis for elliptic quasivariational inequalities

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

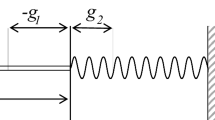
We deal with a class of elliptic quasivariational inequalities with constraints in a reflexive Banach space. We use arguments of monotonicity, convexity and compactness in order to prove a convergence criterion for such inequalities. This criterion allows us to consider a new well-posedness concept in the study of the corresponding inequalities, which extends the classical Tykhonov and Levitin–Polyak well-posedness concepts used in the literature. Then, we introduce a new penalty method, for which we provide a convergence result. Finally, we consider a variational inequality which describes the equilibrium of a spring–rods system, under the action of external forces. We apply our abstract results in the study of this inequality and provide the corresponding mechanical interpretations. We also present numerical simulations which validate our convergence results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Alart, P., Curnier, A.: A mixed formulation for frictional contact problems prone to Newton like solution methods. Comput. Methods Appl. Mech. Eng. 92, 353–375 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  2. Baiocchi, C., Capelo, A.: Variational and Quasivariational Inequalities: Applications to Free-Boundary Problems. Wiley, Chichester (1984)

    MATH  Google Scholar 

  3. Brézis, H.: Equations et inéquations non linéaires dans les espaces vectoriels en dualité. Ann. Inst. Fourier Grenoble) 18, 115–175 (1968)

    Article  MathSciNet  MATH  Google Scholar 

  4. Capatina, A.: Variational Inequalities Frictional Contact Problems, Advances in Mechanics and Mathematics, vol. 31. Springer, New York (2014)

    Book  MATH  Google Scholar 

  5. Dontchev, A.L., Zolezzi, T.: Well-posed Optimization Problems. Lecture Notes Mathematics, vol. 1543. Springer, Berlin (1993)

    Book  MATH  Google Scholar 

  6. Duvaut, G., Lions, J.-L.: Inequalities in Mechanics and Physics. Springer, Berlin (1976)

    Book  MATH  Google Scholar 

  7. Eck, C., Jarušek, J., Krbec, M.: Unilateral Contact Problems: Variational Methods and Existence Theorems, Pure and Applied Mathematics 270. Chapman and Hall, New York (2005)

    Book  MATH  Google Scholar 

  8. Glowinski, R.: Numerical Methods for Nonlinear Variational Problems. Springer, New York (1984)

    Book  MATH  Google Scholar 

  9. Gwinner, J., Jadamba, B., Khan, A.A., Raciti, F.: Uncertainty Quantification in Variational Inequalities: Theory, Numerics, and Applications. Chapman and Hall, New York (2021)

    Book  MATH  Google Scholar 

  10. Gwinner, J., Stephan, E.P.: Advanced Boundary Element Methods—Treatment of Boundary Value, Transmission and Contact Problems, Computational Mathematics 52. Springer, Cham (2018)

    Book  MATH  Google Scholar 

  11. Han, W., Sofonea, M.: Quasistatic Contact Problems in Viscoelasticity and Viscoplasticity, Studies in Advanced Mathematics 30. American Mathematical Society, Providence (2002)

    Book  MATH  Google Scholar 

  12. Hlaváček, I., Haslinger, J., Necǎs, J., Lovíšek, J.: Solution of Variational Inequalities in Mechanics. Springer, New York (1988)

    Book  MATH  Google Scholar 

  13. Huang, X.X., Yang, X.Q., Zhu, D.L.: Levitin–Polyak well-posedness of variational inequality problems with functional constraints. J. Glob. Optim. 44, 159–174 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  14. Kikuchi, N., Oden, J.T.: Contact Problems in Elasticity: A Study of Variational Inequalities and Finite Element Methods. SIAM, Philadelphia (1988)

    Book  MATH  Google Scholar 

  15. Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and their Applications, Classics in Applied Mathematics 31. SIAM, Philadelphia (2000)

    Book  MATH  Google Scholar 

  16. Laursen, T.: Computational Contact and Impact Mechanics. Springer, Netherlands (2002)

    MATH  Google Scholar 

  17. Lucchetti, R.: Convexity and Well-posed Problems. CMS Books in Mathematics. Springer, New York (2006)

    Book  MATH  Google Scholar 

  18. Lucchetti, R., Patrone, F.: A characterization of Tychonov well-posedness for minimum problems with applications to variational inequalities. Numer. Funct. Anal. Optim. 3, 461–476 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  19. Lucchetti, R., Patrone, F.: Some properties of “well-posedness’’ variational inequalities governed by linear operators. Numer. Funct. Anal. Optim. 5, 349–361 (1983)

    Article  MATH  Google Scholar 

  20. Mosco, U.: Convergence of convex sets and of solutions of variational inequalities. Adv. Math. 3, 510–585 (1968)

    Article  MathSciNet  MATH  Google Scholar 

  21. Ochal, A., Przadka, W., Sofonea, M., Tarzia, D.A.: Modelling, analysis and numerical simulation of a spring-rods system with unilateral constraints. Appl. Anal. (2023, in press)

  22. Panagiotopoulos, P.D.: Inequality Problems in Mechanics and Applications. Birkhäuser, Boston (1985)

    Book  MATH  Google Scholar 

  23. Sofonea, M.: Well-posed Nonlinear Problems. A Study of Mathematical Models of Contact. Springer, Berlin (2023)

    Google Scholar 

  24. Sofonea, M., Matei, A.: Mathematical Models in Contact Mechanics: London Mathematical Society Lecture Note Series, vol. 398. Cambridge University Press, Cambridge (2012)

    Book  MATH  Google Scholar 

  25. Sofonea, M., Migórski, S.: Variational-Hemivariational Inequalities with Applications, Pure and Applied Mathematics. CRC Press, Boca Raton (2018)

    MATH  Google Scholar 

  26. Wriggers, P.: Computational Contact Mechanics. Wiley, Chichester (2002)

    MATH  Google Scholar 

  27. Xiao, Y.B., Huang, N.J.: Well-posedness for a class of variational hemivariational inequalities with perturbations. J. Optim. Theory Appl. 151, 33–51 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  28. Xiao, Y.B., Huang, N.J., Wong, M.M.: Well-posedness of hemivariational inequalities and inclusion problems. Taiwan. J. Math. 15, 1261–1276 (2011)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This project has received funding from the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Sklodowska-Curie Grant Agreement No 823731 CONMECH.

Author information

Authors and Affiliations

  1. Laboratoire de Mathématiques et Physique, University of Perpignan Via Domitia, 52 Avenue Paul Alduy, 66860, Perpignan, France

    Mikael Barboteu & Mircea Sofonea

Authors
  1. Mikael Barboteu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mircea Sofonea
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mircea Sofonea.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Barboteu, M., Sofonea, M. Convergence analysis for elliptic quasivariational inequalities. Z. Angew. Math. Phys. 74, 130 (2023). https://doi.org/10.1007/s00033-023-02022-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-023-02022-9

Keywords

Mathematics Subject Classification

Search

Navigation