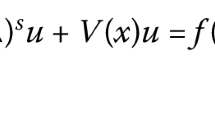Concentration of solutions for fractional Kirchhoff equations with discontinuous reaction

Abstract

In this paper, we consider the following fractional Kirchhoff equation with discontinuous nonlinearity

$$\begin{aligned} \left\{ \begin{array}{ll} \left( \varepsilon ^{2\alpha }a+\varepsilon ^{4\alpha -3}b\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}} u|^2{{\mathrm{d}}}x\right) (-\Delta )^\alpha {u}+V(x)u = H(u-\beta )f(u) &{} \quad \text{ in }\,\,{\mathbb {R}}^3, \\ u\in H^\alpha ({\mathbb {R}}^3),\quad u>0 &{} \quad \text{ in }\,\, {\mathbb {R}}^3, \end{array} \right. \end{aligned}$$

where $\varepsilon ,\beta >0$ are small parameters, $\alpha \in (\frac{3}{4},1)$ and a, b are positive constants, $(-\Delta )^{\alpha }$ is the fractional Laplacian operator, H is the Heaviside function, V is a positive continuous potential, and f is a superlinear continuous function with subcritical growth. By using minimax theorems together with the non-smooth theory, we obtain existence and concentration properties of positive solutions to this non-local system.

1 Introduction and results

This paper is devoted to the qualitative analysis of solutions for the fractional Kirchhoff equation in ${{\mathbb {R}}}^3$. We are concerned with the existence and multiplicity of solutions, as well as with concentration properties of solutions for small values of two positive parameters. A feature of this paper is that the reaction has lack of regularity, which allows to consider larger classes of nonlinearities. The main result is described in the final part of this section.

1.1 Overview

In the last decade, the investigation of nonlinear problems involving fractional and non-local operators has achieved an immense popularity. This is due to the fundamental role of such problems in the analysis of several complex phenomena such as phase transition, game theory, image processing, population dynamics, minimal surfaces and anomalous diffusion, as they are the typical outcome of stochastically stabilization of Lévy processes; see, for instance, the monograph [35] for more details. Moreover, such equations and the associated fractional operators allow us to develop a generalization of quantum mechanics and also to describe the motion of a chain or an array of particles that are connected by elastic springs as well as unusual diffusion processes in turbulent fluid motions and material transports in fractured media; for more details, see [13, 14] and the references therein.

The purpose of this paper is to study the existence and concentration of positive solutions for the following fractional Kirchhoff-type equation:

$$\begin{aligned} \left\{ \begin{array}{ll} \left( \varepsilon ^{2\alpha }a+\varepsilon ^{4\alpha -3}b\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u|^2 {{\mathrm{d}}}x\right) (-\Delta )^\alpha {u}+V(x)u =H(u-\beta )f(u) &{} \quad \text{ in }\,\,{\mathbb {R}}^3, \\ u\in H^\alpha ({\mathbb {R}}^3),\quad u>0 &{} \quad \text{ in }\,\, {\mathbb {R}}^3, \end{array} \right. \end{aligned}$$

(K)

where $\alpha \in (0,1)$ and a, b are positive constants, $\varepsilon ,\beta >0$ are positive parameters, H is the Heaviside function given by

$$\begin{aligned} H(t):=\left\{ \begin{array}{ll} 1,&{} \quad \text{ if }\,\,t>0, \\ 0, &{} \quad \text{ if }\,\, t\le 0. \end{array} \right. \end{aligned}$$

The operator $(-\Delta )^{\alpha }$ is the fractional Laplacian defined as ${{\mathscr {F}}}^{-1}(|\xi |^{2\alpha }{{\mathscr {F}}}(u))$, where ${{\mathscr {F}}}$ denotes the Fourier transform on ${\mathbb {R}}^3$. The potential $V:{\mathbb {R}}^3\rightarrow {\mathbb {R}}$ is a continuous function satisfying the following conditions introduced by Rabinowitz in [40]:

($V_0$):

there exist $V_0,V_\infty >0$ such that

$$\begin{aligned} V_0:=\inf _{x\in {\mathbb {R}}^3}V(x)<\liminf _{|y|\rightarrow \infty }V(y)=V_\infty , \end{aligned}$$

and $f: {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a continuous function fulfilling the following hypotheses:

($f_1$):

$f(t)=0$ for all $t<0$ and $f(t)=o(t^3)$ as $t\rightarrow 0^+$.

($f_2$):

There exists $4<p <2_\alpha ^*-1$ such that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\frac{f(t)}{t^{p}}=0, \end{aligned}$$

where $\alpha \in (\frac{3}{4},1)$, $2_\alpha ^*=\frac{6}{3-2\alpha }$ is the fractional critical exponent.

($f_3$):

The function $t\rightarrow \frac{f(t)}{t^3}$ is increasing in $(0,\infty )$.

($f_4$):

$f(t)\ge \gamma t^{\sigma }$ for all $t>0$ with some $\gamma >0$ and $\sigma \in (3,p-1)$.

Obviously, it follows from the conditions of ($f_1$)-($f_3$) that

$$\begin{aligned} F(t)\ge 0, \quad 4F(t)\le f(t)t, \quad \forall t\in {\mathbb {R}}, \end{aligned}$$

(1.1)

where $F(t)=\int _{0}^{t}f(s)ds$.

When $a=1$, $b=0$, (K) reduces to the following fractional Schrödinger equation

$$\begin{aligned} \varepsilon ^{2\alpha }(-\Delta )^\alpha u+V(x)u =f(u) \quad \text{ in }\,\,{\mathbb {R}}^3, \end{aligned}$$

(1.2)

which has been proposed by Laskin [26] in fractional quantum mechanics as a result of extending the Feynman integrals from the Brownian like to the Lévy like quantum mechanical paths. For such a class of fractional and non-local problems, Caffarelli and Silvestre [14] expressed $(-\Delta )^\alpha$ as a Dirichlet–Neumann map for a certain local elliptic boundary value problem on the half-space. This method is a valid tool to deal with equations involving fractional operators to get regularity and handle variational methods. We refer the readers to [22, 43] and to the references therein. Investigated first in [20] via variational methods, there has been a lot of interest in the study of the existence and multiplicity of solutions for (1.2) when V and f satisfy general conditions. We cite [17, 42] with no attempts to provide a complete list of references.

If $\alpha =\varepsilon =1$ and ${\mathbb {R}}^3$ is replaced by bounded domain $\Omega$, then problem (K) formally reduces to the well-known Kirchhoff equation

$$\begin{aligned} -\left( a+b\int \limits _{\Omega }|\nabla u|^2{{\mathrm{d}}}x\right) \Delta {u}+V(x)u =f(u) \quad \text{ in }\,\,\Omega , \end{aligned}$$

(1.3)

related to the stationary analogue of the Kirchhoff–Schrödinger-type equation

$$\begin{aligned} \frac{\partial ^2 u}{\partial t^2}-\Big (a+b\int \limits _{\Omega }|\nabla u|^2{{\mathrm{d}}}x\Big )\Delta u=f(t,x,u), \end{aligned}$$

where u denotes the displacement, f is the external force, b is the initial tension, and a is related to the intrinsic properties of the string. Equations of this type were first proposed by Kirchhoff [25] in the one-dimensional case, without forcing term and with Dirichlet boundary conditions, in order to describe the transversal free vibrations of a clamped string in which the dependence of the tension on the deformation cannot be neglected. This is a quasilinear partial differential equation; namely, the nonlinear part of the equation contains as many derivatives as the linear differential operator. The Kirchhoff equation is an extension of the classical d’Alembert wave equation for free vibrations of elastic strings. Kirchhoff’s model takes into account the changes in length of the string produced by transverse vibrations. Besides, we also point out that such non-local problems appear in other fields like biological systems, where u describes a process depending on the average of itself; see Alves et al. [1]. The solvability of the Kirchhoff-type equations has been well studied in a general dimension by various authors only after J.-L. Lions [28] introduced an abstract framework to such problems. For more recent results concerning Kirchhoff-type equations in bounded or unbounded domain, we refer, e.g., to [11, 23, 27, 29, 30, 33, 34, 37, 45, 48] and their references.

In the non-local fractional framework, Fiscella and Valdinoci in [21], proposed the following stationary Kirchhoff variational equation with critical growth

$$\begin{aligned} \left\{ \begin{array}{ll} M\left( \int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u|^2\mathrm{d}x\right) (-\Delta )^\alpha {u} =\lambda f(x,u)+|u|^{2_\alpha ^*-2}u &{}\quad \text{ in }\,\,\Omega , \\ u=0 &{}\quad \text{ in }\,\, {\mathbb {R}}^3\setminus \Omega , \end{array} \right. \end{aligned}$$

(1.4)

which models non-local aspects of the tension arising from measurements of the fractional length of the string. They in [21] obtained the existence of non-negative solutions when M and f are continuous functions satisfying suitable assumptions. After that, some existence and multiplicity results to problem (1.4) were obtained in [9, 10, 38, 39, 46] and their references. Recently, several authors have also been paid attention to the existence and multiplicity of solutions for fractional Kirchhoff equations in ${\mathbb {R}}^N$ via variational and topological methods. Precisely, Ambrosio and Isernia [7] considered the fractional Kirchhoff problem

$$\begin{aligned} \left( a+b\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}}x \right) (-\Delta )^\alpha {u} =f(u) \quad \text{ in }\,\,{\mathbb {R}}^3, \end{aligned}$$

(1.5)

where f is an odd subcritical nonlinearity satisfying the well known Berestycki–Lions assumptions. By minimax arguments, the authors establish a multiplicity result in the radial space $H_{{{\mathrm{rad}}}}^\alpha ({\mathbb {R}}^3)$ when the parameter b is sufficiently small. Liu et al. [31] used the monotonicity trick and the profile decomposition to prove the existence of ground states to a fractional Kirchhoff equation with critical nonlinearity in low dimension. In [8], the authors employed penalization method and Lusternik–Schnirelmann category theory to study the existence and multiplicity of solutions for a fractional Schrödinger–Kirchhoff equation with subcritical nonlinearities. see also [6, 24] and their references.

Though there have been many works on the existence and concentration of solutions for Kirchhoff-type problem involving continuous nonlinearities, to the best of our knowledge, it seems that no result has been done for the discontinuous case. In the present paper, we will study a class of fractional Kirchhoff-type problem involving discontinuous nonlinearities. We emphasize that since many obstacle problems and free boundary problems may be reduced to partial differential equations with discontinuous nonlinearities [15, 16], the existence, multiplicity and concentration of solutions for the elliptic problem with discontinuous nonlinearities have been studied in recent years, see [1,2,3,4,5, 41, 47] and their references.

1.2 Main results and strategy

Motivated by the works above, in this paper we aim to study the existence and concentration of positive solutions to the fractional Kirchhoff equation with a discontinuous nonlinearity. In order to study (K), we use the change of variable $x \mapsto \varepsilon x$ and we will look for solutions to

Now we state our main result.

Theorem 1.1

Assume ($V_0$)–($V_3$) holds. Then, there exist $\varepsilon ^*,\beta ^*>0$ such that ($\hbox {K}_\varepsilon$) has a positive solution $u_{\varepsilon ,\beta }$ for $\varepsilon \in (0,\varepsilon ^*)$ and $\beta \in (0,\beta ^*)$. Moreover, there exists a maximum point $x_{\varepsilon ,\beta }\in {\mathbb {R}}^3$ of $u_{\varepsilon ,\beta }$ such that

$$\begin{aligned} \lim \limits _{(\varepsilon ,\beta )\rightarrow (0,0)}V(\varepsilon x_{\varepsilon ,\beta })=V_0. \end{aligned}$$

For such a $x_{\varepsilon ,\beta }$, $v_\varepsilon (x)\equiv u_\varepsilon ( x+x_{\varepsilon ,\beta })$ converges to a positive ground state solution of

$$\begin{aligned} \left( a+b\int \limits _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}}x\right) (-\Delta )^\alpha u+V_0u=f(u),\quad u\in H^\alpha ({\mathbb {R}}^3). \end{aligned}$$

Since we deal with the fractional Kirchhoff-type equation with a discontinuous nonlinearity, some estimates are totally different from those used in the mentioned paper. The minimax method and the non-smooth theory are our main approach in present paper, which are motivated by [3, 29, 44]. The main obstacles are as follows.

Firstly, observe that the energy functional is only locally Lipschitz continuous due to the effect of the Heaviside function, so that we are not able to use variational methods for $C^1$-functionals. For this item, we have to use the variational framework for non-differentiable functionals which will be introduced in Sect. 2. Secondly, for the case with continuous nonlinearity, one can establish one equivalent relationship between the mountain pass level and infimum of energy functional on Nehari manifold, and then use the Fatou lemma to prove the existence of positive ground state solutions for the corresponding limit equation. However, the method of Nehari manifold does not work for locally Lipschitz continuous functionals, and so some new technique needs to be developed to obtain fine estimates to the mountain pass levels. Finally, with the presence of the Kirchhoff term, the main obstacle arises in getting the compactness of the corresponding locally Lipschitz continuous energy functional. Precisely, this does not hold in general: for any $\varphi \in C_0^\infty ({\mathbb {R}}^N)$,

$$\begin{aligned} \int \limits _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u_n|^2{{\mathrm{d}}}x \int \limits _{{\mathbb {R}}^N}(-\Delta )^{\frac{\alpha }{2}}u_n(-\Delta )^{\frac{\alpha }{2}}\varphi {{\mathrm{d}}}x\rightarrow \int \limits _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}}x\int \limits _{{\mathbb {R}}^N}(-\Delta )^{\frac{\alpha }{2}}u(-\Delta )^{\frac{\alpha }{2}}\varphi {{\mathrm{d}}}x, \end{aligned}$$

where $\{u_n\}_{n\in {\mathbb {N}}}$ is a (PS)-sequence of the energy functional satisfying $u_n\rightharpoonup u$ in $H^\alpha ({\mathbb {R}}^3)$. Then, it is not clear that weak limits are critical points of energy functional, which is totally different from those in [2, 3, 23]. For this reason, it is necessary to give one specific profile decomposition of the Kirchhoff term $(\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u_n|^2{{\mathrm{d}}}x)^2$ which enables us to establish refined energy estimate to the mountain pass level. Finally, the above information together with the mountain pass geometry behaviors of energy functional helps us to obtain the compactness (see Lemma 3.6).

Throughout this paper, C will denote a generic positive constant. We denote by $|\cdot |_r$ the $L^r$-norm and use o(1) to denote any quantity which trends to zero when $n\rightarrow \infty$. For any $\rho >0$ and $z\in {\mathbb {R}}^3$, $B_{\rho }(z):=\{x\in {\mathbb {R}}^3:\,|x-z|\le \rho \}$. The symbol $'\rightharpoonup '$ stands for the weak convergence in space E and its dual space $E^*$.

The paper is organized as follows. In Sect. 2, the variational setting and some preliminary lemmas are presented. In Sect. 3, we study existence of positive solutions to ($\hbox {K}_\varepsilon$) with $\varepsilon =1$. Section 4 is devoted by the existence and concentration of positive solutions to ($\hbox {K}_\varepsilon$).

2 Variational setting

In this section, we outline the variational framework for (K) and recall some preliminary lemmas. First, we fix the notations and we recall some useful preliminary results on fractional Sobolev spaces, see [35]. For any $\alpha \in (0,1)$, the fractional Sobolev space $H^{\alpha }({\mathbb {R}}^3)$ is defined by

$$\begin{aligned} H^{\alpha }({\mathbb {R}}^3):=\left\{ u\in L^2({\mathbb {R}}^3):\,\frac{|u(x)-u(y)|}{|x-y|^{\frac{3+2\alpha }{2}}}\in L^2({\mathbb {R}}^3\times {\mathbb {R}}^3)\right\} . \end{aligned}$$

It is known that

$$\begin{aligned} \int _{{\mathbb {R}}^{6}}\frac{|u(x)-u(y)|^2}{|x-y|^{3+2\alpha }}{{\mathrm{d}}}x{{\mathrm{d}}}y =C_\alpha ^{-1}\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}}x, \end{aligned}$$

where

$$\begin{aligned} C_\alpha =\frac{1}{2}\left( \int _{{\mathbb {R}}^3}\frac{1-\cos {\zeta _1}}{|\zeta |^{3+2\alpha }}d\zeta \right) ^{-1}. \end{aligned}$$

We endow the space $H^{\alpha }({\mathbb {R}}^3)$ with the norm

$$\begin{aligned} \Vert u\Vert _{H^\alpha ({\mathbb {R}}^3)}:=\left( \int _{{\mathbb {R}}^3}|u|^2{{\mathrm{d}}}x+\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}}x\right) ^{1/2}. \end{aligned}$$

$H^\alpha ({\mathbb {R}}^3)$ is also the completion of $C^\infty _0({\mathbb {R}}^3)$ with $\Vert \cdot \Vert _{H^\alpha ({\mathbb {R}}^3)}$ and it is continuously embedded into $L^q({\mathbb {R}}^3)$ for $q\in [2,2_\alpha ^*]$. The homogeneous space $D^{\alpha ,2}({\mathbb {R}}^3)$ is

$$\begin{aligned} D^{\alpha ,2}({\mathbb {R}}^3):=\left\{ u\in L^{2^*_{\alpha }}({\mathbb {R}}^3):\,\frac{|u(x)-u(y)|}{|x-y|^{\frac{3+2\alpha }{2}}}\in L^2({\mathbb {R}}^3\times {\mathbb {R}}^3)\right\} , \end{aligned}$$

and it is also the completion of $C^\infty _0({\mathbb {R}}^3)$ with respect to the norm

$$\begin{aligned} \Vert u\Vert _{D^{\alpha ,2}}:=\left( \int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}}x\right) ^{1/2}. \end{aligned}$$

Let

$$\begin{aligned} E:=\left\{ u\in H^{\alpha }({\mathbb {R}}^3):\,\int _{{\mathbb {R}}^3}V(x)u^2{{\mathrm{d}}}x<\infty \right\} \end{aligned}$$

be the Hilbert space equipped with the inner product

$$\begin{aligned} \langle u,v\rangle _{E} :=a\int _{{\mathbb {R}}^3} (-\Delta )^{\frac{\alpha }{2}}u (-\Delta )^{\frac{\alpha }{2}}v \,{{\mathrm{d}}}x+\int _{{\mathbb {R}}^3}V(x)uv \,{{\mathrm{d}}}x, \end{aligned}$$

and the corresponding induced norm

$$\begin{aligned} \Vert u\Vert :=\left( \int _{{\mathbb {R}}^3}a|(-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}}x+\int _{{\mathbb {R}}^3}V(x)u^2{{\mathrm{d}}}x\right) ^{1/2}. \end{aligned}$$

We now recall some definitions and basic results on the critical point theory of locally Lipschitz continuous functionals as developed by Chang [16], Clarke [18].

Let E be a real Banach space. A functional $I : E\rightarrow {\mathbb {R}}$ is locally Lipschitz continuous, $I\in Lip_{loc}(E, {\mathbb {R}})$ for short, if given $u\in E$ there is an open neighborhood $V:=V_u\subset E$ and some constant $K=K_{V}> 0$ such that

$$\begin{aligned} |I(v_2)-I(v_1)|\le K\Vert v_2-v_1\Vert ,\quad v_i\in V,\,\,i=1,2. \end{aligned}$$

The directional derivative of I at u in the direction of $v\in E$ is defined by

$$\begin{aligned} I^0(u;v)=\lim \limits _{h\rightarrow 0}\sup \limits _{\lambda \downarrow 0}\frac{I(u+h+\lambda v)-I(u+h)}{\lambda }. \end{aligned}$$

So $I^0(u;\cdot )$ is continuous, convex and its subdifferential at $z\in E$ is given by

$$\begin{aligned} \partial I^0(u;z)=\{\mu \in E^*;\,\,I^0(u;v)\ge I^0(u;z) +\langle \mu ,v-z\rangle ,\,\, v\in E\}, \end{aligned}$$

where $\langle \cdot ,\cdot \rangle$ is the duality pairing between $E^*$ and E. The generalized gradient of I at u is the set

$$\begin{aligned} \partial I(u)=\{\mu \in E^*; \langle \mu ,v\rangle \le I^0(u; v), v\in E\}. \end{aligned}$$

Since $I^0(u;0)=0$, $\partial I(u)$ is the subdifferential of $I^0(u;0)$. A few definitions and properties will be recalled below. $\partial I(u)\subset E^*$ is convex, non-empty and $\hbox {weak}^*$-compact,

$$\begin{aligned} \lambda (u)=\min \{\Vert \mu \Vert _{E^*};\,\mu \in \partial I(u)\}, \end{aligned}$$

and

$$\begin{aligned} \partial I(u)=\{I'(u)\},\quad \text {if}\,\, I\in C^1(E,{\mathbb {R}}). \end{aligned}$$

A critical point of I is an element $u_0\in E$ such that $0\in \partial I (u_0)$ and a critical value of I is a real number c such that $I(u_0) = c$ for some critical point $u_0\in E$.

By a solution for ($\hbox {K}_\varepsilon$), we understand as a function $u\in W_{loc}^{2\alpha ,\frac{p+1}{p}}({\mathbb {R}}^3)\cap H^\alpha ({\mathbb {R}}^3)$ verifying

where $f_H(t)=H(t-\beta )f(t)$, ${\overline{f}}_H(t)=\limsup _{\delta \rightarrow 0^+}{\overline{f}}_H(t+\delta )$ and ${\underline{f}}_H(t)=\liminf _{\delta \rightarrow 0^+}f_H(t-\delta )$.

Now, we recall the following mountain pass theorem which was established in Radulescu [41].

Theorem 2.1

([41]) Let $I\in Lip_{loc}(E,{\mathbb {R}})$ with $I(0)=0$ and satisfying the following hypotheses:

• (i) there are $r>0$ and $\rho >0$ such that $I(u)\ge \rho$ for $\Vert u\Vert =r,\,u\in E$;

• (ii) there exists $e\in E\setminus B_r(0)$ with $I(e)<0$.

We set

$$\begin{aligned} c_\beta = \inf \limits _{\gamma \in \Gamma }\max \limits _{s\in [0,1]}I{(\gamma (s))}>0, \end{aligned}$$

where

$$\begin{aligned} \Gamma :=\{\gamma \in C([0,1],E)\,\, |\,\,\gamma (0)=0,\, I(\gamma (1))<0\}. \end{aligned}$$

Then, $c\ge \rho$ and there is a sequence $\{u_n\}\subset E$ verifying $I(u_n)\rightarrow c_\beta$ and $\lambda _n(u_n)\rightarrow 0$ in $E'$.

Lemma 2.2

([16, 18]) Let $\{u_n\}\subset E$ and $\{\rho _n\}\subset E^*$ with $\rho _n\in \partial I(u_n)$. If $u_n\rightarrow u$ in E and $\rho _n\rightharpoonup \rho$ in $E^*$, then $\rho _0\in \partial I(u)$.

Lemma 2.3

([16, 18]) Let $R>0$ and $\Psi (u)=\int _{{\mathbb {R}}^3} G(u){{\mathrm{d}}}x$ and $\Psi _{R}(v)=\int _{B_R(0)}G(v){{\mathrm{d}}}x$, where $G(t)=\int _{0}^tg(s)ds$. Then, $\Psi \in Lip_{loc}(L^{p+1}({\mathbb {R}}^3),{\mathbb {R}})$, $\Psi _{R}\in Lip_{loc}(L^{p+1}(B_R(0)),{\mathbb {R}})$, $\partial \Psi (u)\in L^{\frac{p+1}{p}}({\mathbb {R}}^3)$ and $\partial \Psi _R(u)\in L^{\frac{p+1}{p}}(B_R(0))$. Moreover, if $\rho \in \partial \Psi (u)$ and $\zeta \in \partial \Psi _R(v)$, then

$$\begin{aligned} \rho (x)\in [{\underline{g}}(u(x)),{\overline{g}}(u(x))] \quad \hbox {a. e. in}\,\,{\mathbb {R}}^3 \end{aligned}$$

and

$$\begin{aligned} \zeta (x)\in [{\underline{g}}(v(x)),{\overline{g}}(v(x))] \quad \text {a. e. in}\,\,B_R(0). \end{aligned}$$

Lemma 2.4

(Lions lemma, see [42]) Assume that $\{u_n\}_{n\in {\mathbb {N}}}$ is bounded in $H^\alpha ({\mathbb {R}}^3)$ and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\sup \limits _{y\in {\mathbb {R}}^3} \int _{B_{r}(y)}|u_n|^2{{\mathrm{d}}}x=0, \end{aligned}$$

for some $r>0$. Then, $u_n\rightarrow 0$ in $L^s({\mathbb {R}}^3)$ for all $s\in (2,2_\alpha ^*)$.

3 Existence of positive solutions to ($\hbox {K}_\varepsilon$) with $\varepsilon =1$

The energy functional associated with ($\hbox {K}_\varepsilon$) with $\varepsilon =1$, $I:E\rightarrow {\mathbb {R}}$ is defined as

$$\begin{aligned} I_\beta (u)=\frac{1}{2}\Vert u\Vert ^2+\frac{b}{4}\left( \int _{{\mathbb {R}}^3}| (-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}}x\right) ^2 -\int _{{\mathbb {R}}^3}F_H(u){{\mathrm{d}}}x,\quad u\in E, \end{aligned}$$

with $F_H(u)=\int _{0}^{u}f_{H}(s)ds$. Obviously, $I_\beta \in Lip_{loc}(H^\alpha ({\mathbb {R}}^3),{\mathbb {R}})$.

We now verify the functional $I_\beta$ satisfies the mountain pass geometry.

Lemma 3.1

The following properties hold:

• (i) there are $r>0$ and $\rho >0$ such that $I_\beta (u)\ge \rho$ for $\Vert u\Vert =r,\,u\in E$;

• (ii) there exists $v\in E\setminus B_r(0)$ with $I_\beta (v)<0$.

Proof

(i) Observe from the definition of H that for $\beta >0$, there exists $C_\beta >0$ such that

$$\begin{aligned} f_H(t)\le C_\beta t^p, \quad \text {for all}\,\, t\in {\mathbb {R}}. \end{aligned}$$

(3.1)

So from Sobolev’s imbedding inequality, we infer that

$$\begin{aligned} I_\beta (u)\ge \frac{1}{2}\Vert u\Vert ^2-\frac{1}{p+1}\int _{{\mathbb {R}}^3}|u|^{p+1}{{\mathrm{d}}}x\ge \frac{1}{2}\Vert u\Vert ^2-C\Vert u\Vert ^{p+1}. \end{aligned}$$

Hence, there exist $r,\rho >0$, independent of $\beta$, such that for $\Vert u\Vert =r$, $I_\beta (u)\ge \rho >0$.

(ii) Take $e\in C_0^\infty ({\mathbb {R}}^3)\setminus \{0\}$ with $e>0$ and $\Theta :=mes\{x|\,e(x)>\beta \}>0$, then by $(f_4)$ one has

$$\begin{aligned} \begin{aligned} I_\beta (te)&=\frac{t^2}{2}\Vert e\Vert ^2+\frac{bt^4}{4}\left( \int _{{\mathbb {R}}^3}| (-\Delta )^{\frac{\alpha }{2}}e|^2{{\mathrm{d}}}x\right) ^2 -\int _{{\mathbb {R}}^3}F_H(te){{\mathrm{d}}}x\\&\le \frac{t^2}{2}\Vert e\Vert ^2+\frac{bt^4}{4}\left( \int _{{\mathbb {R}}^3}| (-\Delta )^{\frac{\alpha }{2}}e|^2{{\mathrm{d}}}x\right) ^2 -\int _{\{te(x)>\beta \}}F(te)-F(\beta ){{\mathrm{d}}}x\\&\le \frac{t^2}{2}\Vert e\Vert ^2+\frac{bt^4}{4}\left( \int _{{\mathbb {R}}^3}| (-\Delta )^{\frac{\alpha }{2}}e|^2{{\mathrm{d}}}x\right) ^2 -\frac{\gamma t^{\sigma +1}}{\sigma +1}\int _{\Theta }|e|^{\sigma +1}{{\mathrm{d}}}x+F(\beta )\cdot |supt \{e(x)\}|, \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} I_\beta (te)\rightarrow -\infty ,\quad \text {as}\quad t\rightarrow +\infty . \end{aligned}$$

(3.2)

So, take $t_0>0$ large enough, then $v = t_0e$ satisfies $v\in E\setminus B_r(0)$ with $I(v)<0$. $\square$

Combining Lemma 3.1 with Theorem 2.1, there exists a sequence $\{u_n\}\subset E$ satisfying

$$\begin{aligned} I_\beta (u_n)\rightarrow c_\beta \quad and \quad \lambda _\beta (u_n)\rightarrow 0, \end{aligned}$$

(3.3)

where $c_\beta$ is the mountain pass level of the functional $I_\beta$. In what follows, we show that sequence $\{u_n\}$ is bounded in E.

Lemma 3.2

The sequence $\{u_n\}$ is bounded in E.

Proof

Set

$$\begin{aligned} A(u):=\frac{1}{2}\Vert u\Vert ^2+\frac{b}{4}\left( \int _{{\mathbb {R}}^3}| (-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}}x\right) ^2,\quad B(u):=\int _{{\mathbb {R}}^3}F_H(u){{\mathrm{d}}}x. \end{aligned}$$

From now on, we consider $\{w_n\}\subset H^\alpha ({\mathbb {R}}^3)^*$ such that $\lambda _{\beta }(u_n)=\Vert \omega _n\Vert _{E^*}$ and $\omega _n=A'(u_n)-\rho _n$, where $\{\rho _n\}\subset \partial B(u_n)$. Then,

$$\begin{aligned} \Vert u_n\Vert ^2+b\left( \int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u_n|^2{{\mathrm{d}}}x\right) ^2 =\langle \omega _n+\rho _n,u_n\rangle . \end{aligned}$$

(3.4)

Since $\rho _n\in [{\underline{f}}_H(u_n(x)),{\overline{f}}_H(u_n(x))]$ a.e in ${\mathbb {R}}^3$, then by (1.1) we have

$$\begin{aligned} \langle \rho _n,u_n\rangle \ge \int _{{\mathbb {R}}^3}{\underline{f}}_H(u_n)u_n{{\mathrm{d}}}x\ge \int _{\{u_n>\beta \}}f(u_n)u_n{{\mathrm{d}}}x \ge 4\int _{\{u_n>\beta \}}F(u_n){{\mathrm{d}}}x. \end{aligned}$$

It then follows from (3.4) that

$$\begin{aligned} \begin{aligned} c_\beta +o_n(1)&=I_\beta (u_n)-\frac{1}{4}\langle \omega _n,u_n\rangle \\&=\frac{1}{4}\Vert u_n\Vert ^2+\frac{1}{4}\langle \rho _n,u_n\rangle -\int _{\{u_n>\beta \}}F_H(u_n){{\mathrm{d}}}x\\&\ge \frac{1}{4}\Vert u_n\Vert ^2, \end{aligned} \end{aligned}$$

(3.5)

which finishes the proof of the lemma. $\square$

Recalling (3.3) and Lemma 3.2, up to subsequence, there exists a subsequence of $\{u_n\}$ (still denoted by $\{u_n\}$) such that

$$\begin{aligned} u_n\rightharpoonup u_0\quad \text {in}\,\,E, \quad \quad u_n\rightarrow u_0\quad \text {in}\,\,L_{loc}^s({\mathbb {R}}^3),\,\,\,s\in (2,2_\alpha ^*). \end{aligned}$$

(3.6)

Lemma 3.3

Let $\{\rho _n\}\subset \partial B(u_n)$ with $\rho _n\rightharpoonup \rho _0$ in $L^{\frac{p+1}{p}}({\mathbb {R}}^3)$. Then,

$$\begin{aligned} \rho _0(x)\in [{\underline{f}}_H(u(x)),{\overline{f}}_H(u(x))]\quad a.e\,\,\text {in}\,\,{\mathbb {R}}^3. \end{aligned}$$

Proof

Since $u_n\rightharpoonup u$ in E, one has $u_n\rightarrow u$ in $L^{p+1}_{loc}({\mathbb {R}}^3)$. Hence, for any $\varphi \in C_0^\infty ({\mathbb {R}}^3)$, the following holds

$$\begin{aligned} \int _{{\mathbb {R}}^3}u_n\varphi {{\mathrm{d}}}x\rightarrow \int _{{\mathbb {R}}^3}u\varphi {{\mathrm{d}}}x,\quad \int _{{\mathbb {R}}^3}\rho _n\varphi {{\mathrm{d}}}x\rightarrow \int _{{\mathbb {R}}^3}\rho _0\varphi {{\mathrm{d}}}x. \end{aligned}$$

Recalling Lemma 2.2 we get

$$\begin{aligned} \rho _0(x)\in [{\underline{f}}_H(u(x)),{\overline{f}}_H(u(x))]\quad a.e\,\,\text {in}\,\,{\mathbb {R}}^3. \end{aligned}$$

The proof is now complete. $\square$

Lemma 3.4

As for sequence $\{u_n\}\subset E$ defined in (3.3), there exists a sequence $\{y_n\}\subset {\mathbb {R}}^3$ and constants $R,\tau >0$ such that

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\int _{B_R(y_n)}u_n^2{{\mathrm{d}}}x\ge \tau >0. \end{aligned}$$

(3.7)

Proof

Suppose by contradiction that (3.7) does not hold. Then, it follows from Lemma 2.4 that $u_n\rightarrow 0$ in $L^s({\mathbb {R}}^3)$ for $s\in (2, 2_\alpha ^*)$. By (3.1) and (3.4), there exists $\{\rho _n\}\subset \partial B(u_n)$ with $\rho _n\in [{\underline{f}}_H(u_n(x)),{\overline{f}}_H(u_n(x))]$ a.e in ${\mathbb {R}}^3$ such that

$$\begin{aligned} \begin{aligned} \Vert u_n\Vert ^2&\le \int _{{\mathbb {R}}^3} \rho _nu_n{{\mathrm{d}}}x\le \int _{{\mathbb {R}}^3}{\overline{f}}_H(u_n)u_n{{\mathrm{d}}}x\\&\le \int _{\{u_n\ge \beta \}}f(u_n)u_n{{\mathrm{d}}}x\rightarrow 0. \end{aligned} \end{aligned}$$

(3.8)

This implies that $u_n\rightarrow 0$ in E. Furthermore, $I_\beta (u_n)\rightarrow 0$ as $n\rightarrow \infty$. This contradicts $c_\beta >0$. The proof is complete. $\square$

Let $c_\infty$ be the mountain pass level associated with the functional $I_\infty : H^\alpha ({\mathbb {R}}^3)\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} \begin{aligned} I_\infty (u)= \frac{1}{2}\int _{{\mathbb {R}}^3}(a|(-\Delta )^{\frac{\alpha }{2}} u|^2+V_\infty u^2){{\mathrm{d}}}x+\frac{b}{4}\left( \int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}} u|^2{{\mathrm{d}}}x\right) ^2-\int _{{\mathbb {R}}^3}F(u){{\mathrm{d}}}x. \end{aligned} \end{aligned}$$

(3.9)

Lemma 3.5

Assume that there exists $\beta _1>0$ small such that $(1+\beta ^2)c_\beta <c_\infty$ for fixed $\beta \in (0,\beta _1)$, then $u_0\not =0$.

Proof

Suppose on the contrary that $u_0=0$. The Sobolev’s embedding together with Lemma 4.2 yields $\{y_n\}$ is unbounded. That is, up to subsequence, $|y_n|\rightarrow +\infty$. Let us set $v_n(x):=u_n(x+y_n)$. It is easy to check that $\{v_n\}$ is bounded in $H^\alpha ({\mathbb {R}}^3)$. Recalling Lemma 4.2, up to subsequence, there exists $v\in E\setminus \{0\}$ such that for $s\in [1,2_\alpha ^*)$

$$\begin{aligned} v_n\rightharpoonup v\quad \text {in}\quad E,\quad \quad v_n\rightarrow v\quad \text {in}\quad L_{loc}^s({\mathbb {R}}^3). \end{aligned}$$

(3.10)

For any $R>0$, let $\varphi _R\in C_0^\infty ({\mathbb {R}}^3)$ be such that $\varphi _R(x)=1$ in $B_R$ and $\varphi _R(x)=0$ in ${\mathbb {R}}^3\setminus \{B_{2R}\}$, with $0 \le \varphi _R\le 1$ and $|\nabla \varphi _R|\le \frac{C}{R}$ , where C is a constant independent of R. Since the sequence $\{(\varphi _R v_n)(\cdot -y_n)\}$ is bounded in E, the following holds

$$\begin{aligned} \begin{aligned}&(a+b\Vert u_n\Vert ^2_{D^{2,\alpha }})\int _{{\mathbb {R}}^3}(-\Delta )^{\frac{\alpha }{2}} u_n(-\Delta )^{\frac{\alpha }{2}}(\varphi _R v_n)(\cdot -y_n){{\mathrm{d}}}x +\int _{{\mathbb {R}}^3}V(x)u_n(\varphi _R v_n)(\cdot -y_n){{\mathrm{d}}}x\\&\quad =\int _{{\mathbb {R}}^3}\rho _n(\varphi _R v_n)(\cdot -y_n){{\mathrm{d}}}x+o_n(1),\quad v\in E. \end{aligned} \end{aligned}$$

(3.11)

Using the fact that $\rho _n\in [{\underline{f}}_H(u_n(x)),{\overline{f}}_H(u_n(x))]$ a.e in ${\mathbb {R}}^3$, we have

$$\begin{aligned} \begin{aligned} \int _{{\mathbb {R}}^3}\rho _n(\varphi _R v_n)(\cdot -y_n){{\mathrm{d}}}x\le \int _{{\mathbb {R}}^3}{\overline{f}}_H(v_n)v_n\varphi _R {{\mathrm{d}}}x\le \int _{{\mathbb {R}}^3}f(v_n)v_n\varphi _R {{\mathrm{d}}}x. \end{aligned} \end{aligned}$$

(3.12)

It follows from (3.10) that

$$\begin{aligned} \begin{aligned} \int _{{\mathbb {R}}^3}f(v_n)v_n\varphi _R {{\mathrm{d}}}x=\int _{{\mathbb {R}}^3}f(v)v\varphi _R {{\mathrm{d}}}x+o_n(1). \end{aligned} \end{aligned}$$

(3.13)

Observe that

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^3}(-\Delta )^{\frac{\alpha }{2}} u_n(-\Delta )^{\frac{\alpha }{2}} (\varphi _R v_n)(\cdot -y_n){{\mathrm{d}}}x\\&\quad =C_\alpha \int _{{\mathbb {R}}^{3}\times {\mathbb {R}}^{3}}\frac{[v_n(x)-v_n(y) ]^2\varphi _R(x)}{|x-y|^{3+2\alpha }}{{\mathrm{d}}}x{{\mathrm{d}}}y\\&\qquad +C_\alpha \int _{{\mathbb {R}}^{3}\times {\mathbb {R}}^{3}}\frac{[v_n(x)-v_n(y) ][\varphi _R(x)-\varphi _R(y)]}{|x-y|^{3+2\alpha }}v_n(y){{\mathrm{d}}}x{{\mathrm{d}}}y. \end{aligned} \end{aligned}$$

(3.14)

Using the Hölder inequality, the boundedness of $\{u_n\}$ in E and $|\nabla \varphi _R|\le \frac{C}{R}$, we have

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^{3}\times {\mathbb {R}}^{3}}\frac{[v_n(x)-v_n(y)][\varphi _R(x) -\varphi _R(y)]}{|x-y|^{3+2\alpha }}v_n(y){{\mathrm{d}}}x{{\mathrm{d}}}y\\&\quad \le \Vert v_n\Vert _{D^{2,\alpha }}^2\bigg (\int _{{\mathbb {R}}^{3}\times {\mathbb {R}}^{3}} \frac{[\varphi _R(x)-\varphi _R(y)]^2}{|x-y|^{3+2\alpha }}v_n^2(y) {{\mathrm{d}}}x{{\mathrm{d}}}y\bigg )^{1/2}\\&\quad \le \Vert v_n\Vert _{D^{2,\alpha }}^2\bigg (\frac{C}{R^2}\int _{{\mathbb {R}}^{3}} \int _{|x-y|\le 4R}\frac{1}{|x-y|^{1+2\alpha }}v_n^2(y){{\mathrm{d}}}x{{\mathrm{d}}}y\bigg )^{1/2}\\&\quad \le \frac{C}{R}\Vert v_n\Vert _{D^{2,\alpha }}^2\bigg (\int _{{\mathbb {R}}^{3}} v_n^2(y){{\mathrm{d}}}y\int _{0}^{4R}\frac{1}{r^{2\alpha -1}}dr\bigg )^{1/2}\\&\quad \le \frac{C}{R^\alpha }, \end{aligned} \end{aligned}$$

(3.15)

where we have used polar coordinate transformation in the third inequality. Taking into account (3.11)-(3.15), by Fatou’s lemma we infer that

$$\begin{aligned} \begin{aligned}&(a+b\Vert v\Vert ^2_{D^{2,\alpha }})C_\alpha \int _{{\mathbb {R}}^{3}\times {\mathbb {R}}^{3}} \frac{[v(x)-v(y)]^2\varphi _R(x)}{|x-y|^{3+2\alpha }}{{\mathrm{d}}}x{{\mathrm{d}}}y +\int _{{\mathbb {R}}^3}V_\infty v^2\varphi _R{{\mathrm{d}}}x\\&\quad \le \int _{{\mathbb {R}}^3}f(v)v\varphi _R {{\mathrm{d}}}x+\frac{C}{R^\alpha }. \end{aligned} \end{aligned}$$

(3.16)

Let $R\rightarrow +\infty$ in (3.16), then

$$\begin{aligned} (a+b\Vert v\Vert ^2_{D^{2,\alpha }})\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}} v|^2{{\mathrm{d}}}x +\int _{{\mathbb {R}}^3}V_\infty v^2{{\mathrm{d}}}x\le \int _{{\mathbb {R}}^3}f(v)v{{\mathrm{d}}}x. \end{aligned}$$

(3.17)

Since $v\not =0$, there exists $t\in (0,1)$ such that $tv\in {\mathcal {N}}$ (see [23]), where ${\mathcal {N}}$ is the Nehari manifold associated with $I_\infty$ given by

$$\begin{aligned} {\mathcal {N}}:=\{u\in E\setminus \{0\};\,\,I'_\infty (u)u=0\}. \end{aligned}$$

As a consequence, using ($f_3$) and Fatou’s lemma, we have

$$\begin{aligned} \begin{aligned} I_\infty (tv)-\frac{1}{4}I'_\infty (tv)tv&= \frac{t^2}{4}\int _{{\mathbb {R}}^3}[(|(-\Delta )^{\frac{\alpha }{2}}v|^2 +V_\infty v^2]{{\mathrm{d}}}x+\int _{{\mathbb {R}}^3}\left[ \frac{1}{4}f(tv)tv-F(tv)\right] {{\mathrm{d}}}x\\&\le \liminf \limits _{n\rightarrow \infty }\left( \frac{1}{4}\Vert u_n\Vert ^2+\int _{{\mathbb {R}}^3} \left( \frac{1}{4}f(u_n)u_n-F(u_n)\right) {{\mathrm{d}}}x\right) .\\ \end{aligned} \end{aligned}$$

(3.18)

Recalling the definitions of ${\underline{f}}_H$ and ${\overline{f}}_H$, we deduce from ($f_1$) that there exists $\beta _1>0$ such that $f(t)\le V_0t^3$ for $t\in (0,\beta _1)$ and then by (3.5) and $c_\beta <c_\infty$, we have for large n

$$\begin{aligned} \begin{aligned} \int _{{\mathbb {R}}^3}f(u_n)u_n&=\int _{\{u_n\le \beta \}}f(u_n)u_n+\int _{\{u_n>\beta \}}f(u_n)u_n\\&\le \beta ^2\Vert u_n\Vert ^2 +\int _{{\mathbb {R}}^3}{\underline{f}}_H(u_n)u_n\\&\le 4\beta ^2(c_\beta +o_n(1)) +\int _{{\mathbb {R}}^3}{\underline{f}}_H(u_n)u_n \end{aligned} \end{aligned}$$

(3.19)

for any fixed $\beta \in (0,\beta _1)$. Putting (3.19) into (3.18), by $c_\infty =\inf _{u\in {\mathcal {N}}}I(u)$ (see [23]) and (3.18), one has

$$\begin{aligned} \begin{aligned} c_\infty&\le I_\infty (tv)-\frac{1}{4}I'_\infty (tv)tv\\&\le \liminf \limits _{n\rightarrow \infty }\left( \frac{1}{4}\Vert u_n\Vert ^2+\beta ^2(c_\beta +o_n(1)) +\int _{{\mathbb {R}}^3}\left( \frac{1}{4}{\underline{f}}_H(u_n)u_n-F_H(u_n)\right) {{\mathrm{d}}}x\right) \\&\le \liminf \limits _{n\rightarrow \infty }\left( \frac{1}{4}\Vert u_n\Vert ^2+\beta ^2(c_\beta +o_n(1)) +\int _{{\mathbb {R}}^3}\left( \frac{1}{4}\rho _nu_n-F_H(u_n)\right) {{\mathrm{d}}}x\right) \\&\le \liminf \limits _{n\rightarrow \infty }\left( I_\beta (u_n) -\frac{1}{4}\langle A'(u_n)-\rho _n, u_n\rangle +\beta ^2(c_\beta +o_n(1))\right) \\&=(1+\beta ^2)c_\beta , \end{aligned} \end{aligned}$$

which is a contradiction. Therefore, $u_0\ge 0$ and $u_0\not =0$. $\square$

The next result establishes the existence of mountain pass solutions to ($\hbox {K}_\varepsilon$) with $\varepsilon =1$; that is, there exists $u_0\in E$ satisfying

$$\begin{aligned} I_\beta (u_0)=c_\beta \quad \quad \text {and}\quad \quad 0\in \partial I_\beta (u_0), \end{aligned}$$

where $c_\beta$ is the mountain pass level associated with $I_\beta$.

Lemma 3.6

Assume that there exists $\beta _1>0$ such that $(1+\beta ^2)c_\beta <c_\infty$ for fixed $\beta \in (0,\beta _1)$, then ($\hbox {K}_\varepsilon$) with $\varepsilon =1$ has a non-trivial solution $u_0\in E$, and set $\Lambda :=\{x\in {\mathbb {R}}^3:\,u_0(x)=\beta \}$ has null measure. Moreover,

$$\begin{aligned} I_{\beta }(u_0)=\max \limits _{t\ge 0}I_{\beta }(tu_0). \end{aligned}$$

Proof

In view of Lemma 3.5, $u_0$ given in (3.6) is nonzero. Hence, there exists constant ${\mathcal {B}}>0$ such that $\Vert u_n\Vert ^2_{D^{\alpha ,2}}\rightarrow {\mathcal {B}}$ as $n\rightarrow \infty$, where $\{u_n\}$ has been defined in (3.3). Indeed, we need to prove that $u_0\in W_{loc}^{2\alpha ,\frac{p+1}{p}}({\mathbb {R}}^3)\cap H^\alpha ({\mathbb {R}}^3)$ and $u_0$ solves

$$\begin{aligned} \left( a+b\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}}x\right) (-\Delta )^\alpha {u}+V( x)u \in [{\underline{f}}_H(u(x)),{\overline{f}}_H(u(x))] \quad a.e.\,\text{ in }\,\,{\mathbb {R}}^3. \end{aligned}$$

Since $\{u_n\}\subset E$ is a (PS)$_{c_\beta }$ sequence, there exists $\{\rho _n\}\subset \partial B(u_n)$ such that

$$\begin{aligned} \begin{aligned} \int _{{\mathbb {R}}^3}&\big (a(-\Delta )^{\frac{\alpha }{2}} u_n(-\Delta )^{\frac{\alpha }{2}} v+V(x)u_nv\big ){{\mathrm{d}}}x +b\bigg (\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u_n|^2{{\mathrm{d}}}x \bigg )^2\int _{{\mathbb {R}}^3}(-\Delta )^{\frac{\alpha }{2}}u_n(-\Delta )^{\frac{\alpha }{2}}v{{\mathrm{d}}}x\\&=\int _{{\mathbb {R}}^3}\rho _nv{{\mathrm{d}}}x,\quad v\in E, \end{aligned} \end{aligned}$$

(3.20)

with $\rho _n\in [{\underline{f}}_H(u_n(x)),{\overline{f}}_H(u_n(x))]$ a.e. in ${\mathbb {R}}^3$. It then follows from the boundedness of $\{u_n\}$, the definition of H, ($f_1$) and ($f_2$) that sequence $\{\rho _n\}$ is bounded in $L^{\frac{p+1}{p}}({\mathbb {R}}^3)$. Thus, up to subsequence, there exists $\rho _0\in L^{\frac{p+1}{p}}({\mathbb {R}}^3)$ such that

$$\begin{aligned} \rho _n\rightharpoonup \rho _0\quad \quad \text {in}\quad L^{\frac{p+1}{p}}({\mathbb {R}}^3), \end{aligned}$$

(3.21)

which implies by (3.6) that for any $v\in E$

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^3}\big [a(-\Delta )^{\frac{\alpha }{2}} u_0(-\Delta )^{\frac{\alpha }{2}} v+V(x)u_0v\big ]{{\mathrm{d}}}x +b{\mathcal {B}}\int _{{\mathbb {R}}^3}(-\Delta )^{\frac{\alpha }{2}}u_0(-\Delta )^{\frac{\alpha }{2}}v{{\mathrm{d}}}x=\int _{{\mathbb {R}}^3}\rho _0v{{\mathrm{d}}}x. \end{aligned} \end{aligned}$$

(3.22)

Recalling Lemma 3.3, one has $\rho _0\in [{\underline{f}}_H(u_0(x)),{\overline{f}}_H(u_0(x))]$ a.e in ${\mathbb {R}}^3$. From elliptic regularity theory, we deduce that $u\in W^{2\alpha ,\frac{p+1}{p}}({\mathbb {R}}^3)$. As a consequence, from (3.22), we immediately obtain that $u_0$ is a non-negative weak solution of the following equation

$$\begin{aligned} \left\{ \begin{array}{ll} (a+b{\mathcal {B}})(-\Delta )^\alpha {u}+V(x)u = H(u-\beta )f(u) &{} \quad \text{ a. } \text{ e. } \text{ in }\,\,{\mathbb {R}}^3, \\ u\in H^\alpha ({\mathbb {R}}^3),\quad \end{array} \right. \end{aligned}$$

(3.23)

whose energy functional is

$$\begin{aligned} J_\beta (u)= \frac{a+b{\mathcal {B}}}{2}\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}} u|^2{{\mathrm{d}}}x+\frac{1}{2}\int _{{\mathbb {R}}^3}V(x) u^2{{\mathrm{d}}}x-\int _{{\mathbb {R}}^3}F_H(u){{\mathrm{d}}}x. \end{aligned}$$

By using the Stampacchia theorem, we immediately obtain that $\Lambda =\{x\in {\mathbb {R}}^3:\,u_0(x)=\beta \}$ has null measure for $\beta$ small enough. Using $v=u_0^-:=\min \{u_0,0\}$ in (3.22) and the fact that $\rho _0\in [{\underline{f}}_H(u_0(x)),{\overline{f}}_H(u_0(x))]$ a.e in ${\mathbb {R}}^3$, we have

$$\begin{aligned} (a+b{\mathcal {B}})\int _{{\mathbb {R}}^3}((-\Delta )^{\alpha } u_0 u_0^-+V(x) |u_0^-|^2){{\mathrm{d}}}x=\int _{{\mathbb {R}}^3}\rho _0u_0^-{{\mathrm{d}}}x=0, \end{aligned}$$

which implies that $u_0\ge 0$ (see [32]). Moreover, we can use an iteration method which was firstly introduced in [12] to prove $u_0\in L^\infty ({\mathbb {R}}^3)$. Using Proposition 2.9 in [43] and $2\alpha >1$, we have $u_0\in C^{1,s}({\mathbb {R}}^3)$ for $s\in (0,2\alpha -1)$. Using the maximum principle in [43], we can conclude that $u>0$ in ${\mathbb {R}}^3$.

Note that one of the following cases must occur.

Case 1. ${\mathcal {B}}=\Vert u_0\Vert _{D^{\alpha ,2}}^2$. Thus, $u_n\rightarrow u_0$ in $D^{\alpha ,2}({\mathbb {R}}^3)$ as $n\rightarrow \infty$. It is easy to see from (3.23) that $u_0$ is a non-trivial weak solution of ($\hbox {K}_1$). Moreover, by the Hölder inequality and the fractional Gagliardo–Nirenberg–Sobolev inequality, we have

$$\begin{aligned} \begin{aligned} \bigg |\int _{{\mathbb {R}}^3}(\rho _nu_n-\rho _0u_0){{\mathrm{d}}}x\bigg |&=\bigg |\int _{{\mathbb {R}}^3}\rho _n(u_n-u_0){{\mathrm{d}}}x\bigg | +\bigg |\int _{{\mathbb {R}}^3}(\rho _n-\rho _0)u_0{{\mathrm{d}}}x\bigg |\\&\le \Vert \rho _n\Vert _{\frac{p+1}{p}}\Vert u_n-u_0\Vert ^{p+1}_{p+1}+o_n(1)\\&\le C\Vert \rho _n\Vert _{\frac{p+1}{p}}\Vert u_n-u_0\Vert _{D^{\alpha ,2} }^{\frac{3(p-1)}{2\alpha }}\Vert u_n-u_0\Vert _2^{p+1-\frac{3(p-1)}{2\alpha }}+o_n(1)\\&=o_n(1). \end{aligned} \end{aligned}$$

As a consequence, letting $v=u_n$ in (3.20) and $v=u_0$ in (3.22), one has

$$\begin{aligned} \begin{aligned} \Vert u_n-u_0\Vert ^2=\int _{{\mathbb {R}}^3}(\rho _nu_n-\rho _0u_0){{\mathrm{d}}}x+o_n(1)=o_n(1). \end{aligned} \end{aligned}$$

We conclude that $u_n\rightarrow u_0$ in E as $n\rightarrow \infty$.

Case 2. $\Vert u_0\Vert _{D^{\alpha ,2}}^2<{\mathcal {B}}$. Let us claim that there exists $t^*\in (0,1)$ such that

$$\begin{aligned} \max \limits _{t\ge 0} I_\beta (tu_0)=I_\beta (t^*u_0). \end{aligned}$$

(3.24)

Since $h(t):=I_\beta (tu_0)$ is locally Lipschitz continuous function, h is differentiable almost everywhere. A direct computation shows that there exist $\delta , t_0>0$ such that

$$\begin{aligned} h(t)>0,\quad \text {for all}\,\, t\in (0,\delta )\quad \quad \text {and}\quad \quad h(t)<0\quad \text {for all}\,\, t\ge t_0, \end{aligned}$$

(3.25)

which implies that there exists $t^*>0$ such that (3.24) holds. Let us denote $I\subset {\mathbb {R}}$ by the set of the points where $h'$ does not exist, we have $|I|=0$, where |I| denotes the Lebesgue’s measure of I. The claim is proved by showing that

• (a) $h'(t)>0$ for any $t\in (0,t^*)\cap I^c$ and $h'(t)<0$ for any $t\in (t^*,+\infty )\cap I^c$, where $t^*\in (0,1)$.

Using the chain rule for locally Lipschitz continuous function, there is $w\in \partial I_{\beta }(tu_0)$ such that $h'(t)=\langle w,u_0\rangle$. That is to say, there exists $\rho _0\in \partial B(tu_0)$ satisfying

$$\begin{aligned} h'(t)=t\bigg (\int _{{\mathbb {R}}^3}a|(-\Delta )^{\frac{\alpha }{2}} u_0|^2{{\mathrm{d}}}x+\int _{{\mathbb {R}}^3}V(x)u_0^2{{\mathrm{d}}}x\bigg ) +t^3b\Vert u_0\Vert _{D^{\alpha ,2}}^4-\int _{{\mathbb {R}}^3}\rho _0u_0{{\mathrm{d}}}x. \end{aligned}$$

It follows from $0\in \partial J_{\beta }(u_0)$, $|\Lambda |=0$ and (3.22) that

$$\begin{aligned} (a+b{\mathcal {B}})\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}} u_0|^2{{\mathrm{d}}}x+\int _{{\mathbb {R}}^3}V(x)u_0^2{{\mathrm{d}}}x =\int _{{\mathbb {R}}^3}f_{H}(u_0)u_0{{\mathrm{d}}}x. \end{aligned}$$

(3.26)

Based on the above facts, one has

$$\begin{aligned} h'(t)=t\bigg (\int _{{\mathbb {R}}^3}f_{H}(u_0)u_0{{\mathrm{d}}}x-b{\mathcal {B}}\Vert u_0\Vert _{D^{\alpha ,2}}^2\bigg ) +t^3b\Vert u_0\Vert _{D^{\alpha ,2}}^4-\int _{{\mathbb {R}}^3}\rho _0u_0{{\mathrm{d}}}x, \end{aligned}$$

which implies by $|\Lambda |=0$ and the fact that $\rho _0\in [{\underline{f}}_H(tu_0(x)),{\overline{f}}_H(tu_0(x))]$ a.e in ${\mathbb {R}}^3$ that

$$\begin{aligned} \begin{aligned} h'(t)&\le t\bigg (\int _{{\mathbb {R}}^3}{f}_{H}(u_0)u_0{{\mathrm{d}}}x -\int _{{\mathbb {R}}^3}{\underline{f}}_H(tu_0)u_0{{\mathrm{d}}}x\bigg ) +t^3b\Vert u_0\Vert _{D^{\alpha ,2}}^4-b{\mathcal {B}}t\Vert u_0\Vert _{D^{\alpha ,2}}^2\\&=t^3\bigg (\int _{{\mathbb {R}}^3}\frac{{\underline{f}}_{H}(u_0)}{t^2}u_0{{\mathrm{d}}}x -\int _{{\mathbb {R}}^3}\frac{{\underline{f}}_H(tu_0)}{t^3}u_0{{\mathrm{d}}}x +b\Vert u_0\Vert _{D^{\alpha ,2}}^4-\frac{b{\mathcal {B}}}{t^2}\Vert u_0\Vert _{D^{\alpha ,2}}^2\bigg )\\&\le t^3\bigg (\int _{\{u_0>\beta \}}\frac{f(u_0)}{t^2}u_0{{\mathrm{d}}}x -\int _{\{tu_0>\beta \}}\frac{f(tu_0)}{t^3}u_0{{\mathrm{d}}}x +b\Vert u_0\Vert _{D^{\alpha ,2}}^4-\frac{b{\mathcal {B}}}{t^2}\Vert u_0\Vert _{D^{\alpha ,2}}^2\bigg ). \end{aligned} \end{aligned}$$

(3.27)

Similarly, we can also obtain

$$\begin{aligned} h'(t)\ge t^3\bigg (\int _{\{u_0>\beta \}}\frac{f(u_0)}{t^2}u_0{{\mathrm{d}}}x-\int _{\{tu_0\ge \beta \}}\frac{f(tu_0)}{t^3}u_0{{\mathrm{d}}}x +b\Vert u_0\Vert _{D^{\alpha ,2}}^4-\frac{b{\mathcal {B}}}{t^2}\Vert u_0\Vert _{D^{\alpha ,2}}^2\bigg ). \end{aligned}$$

Define ${\mathcal {H}}:(0,+\infty )\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} {\mathcal {H}}(t):=\int _{\{u_0>\beta \}}\frac{f(u_0)}{t^2}u_0{{\mathrm{d}}}x-\int _{\{tu_0>\beta \}}\frac{f(tu_0)}{t^3}u_0{{\mathrm{d}}}x +b\Vert u_0\Vert _{D^{\alpha ,2}}^4-\frac{b{\mathcal {B}}}{t^2}\Vert u_0\Vert _{D^{\alpha ,2}}^2. \end{aligned}$$

Obviously, ${\mathcal {H}}(1)<0$ due to $\Vert u_0\Vert _{D^{\alpha ,2}}^2<{\mathcal {B}}$. It follows from ($f_1$)-($f_3$) and (3.27) that there exists ${\tilde{t}}\in (0,1)$ such that ${\mathcal {H}}({\tilde{t}})=0$ and $h'(t)<0$ for all $t\in ({\tilde{t}},+\infty )\cap I^c$. Based on (3.25) and the above facts, h has a global maximum in $t=t^*\in (0,{\tilde{t}}]$. Thus, conclusion (a) holds and then the claim is true. Recalling the definition of $c_\beta$, we obtain

$$\begin{aligned} c_\beta \le I_\beta (t^*u_0). \end{aligned}$$

(3.28)

Observe by $|\Lambda |=0$ and the definition of H that

$$\begin{aligned} \int _{\{u_0\le \beta \}}F_H(u_0){{\mathrm{d}}}x=0. \end{aligned}$$

(3.29)

Since $t^*$ is a global maximum point of h(t), there exist sequence $\{t_n\}\subset (t^*,+\infty )\cap I^c$ with $t_n\rightarrow t^*$ and $\rho _n\in \partial B(t_nu_0)$ such that

$$\begin{aligned} h'(t_n)=t\bigg (\int _{{\mathbb {R}}^3}a|(-\Delta )^{\frac{\alpha }{2}} u_0|^2{{\mathrm{d}}}x+\int _{{\mathbb {R}}^3}V(x)u_0^2{{\mathrm{d}}}x\bigg ) +t^3b\Vert u_0\Vert _{D^{\alpha ,2}}^4-\int _{{\mathbb {R}}^3}\rho _nu_0{{\mathrm{d}}}x\le 0, \end{aligned}$$

which implies by (3.28), (3.29), the definition of $I_\beta$ and $t_n\in (0,1)$ that

$$\begin{aligned} \begin{aligned} c_\beta&\le I_\beta (t^*u_0)\\&\le I_\beta (t_nu_0)-\frac{1}{4}h'(t_n)t_n+o_n(1)\\&\le \frac{t_n^2}{4}\Vert u_0\Vert ^2-\int _{{\mathbb {R}}^3}F_H(t_nu_0){{\mathrm{d}}}x +\frac{1}{4}\int _{{\mathbb {R}}^3}\rho _nt_nu_0{{\mathrm{d}}}x+o_n(1)\\&\le \frac{t_n^2}{4}\Vert u_0\Vert ^2+\int _{\{t_nu_0\ge \beta \}} \frac{1}{4}f(t_nu_0)t_nu_0{{\mathrm{d}}}x+o_n(1)\\&\quad -\int _{\{t_nu_0>\beta \}}[F(t_nu_0)-F(\beta )]{{\mathrm{d}}}x -\int _{\{t_nu_0\le \beta \}}F_H(t_nu_0){{\mathrm{d}}}x\\&=\frac{t_n^2}{4}\Vert u_0\Vert ^2+\int _{\{t_nu_0\ge \beta \}} \left[ \frac{1}{4}f(t_nu_0)t_nu_0-F(t_nu_0)\right] {{\mathrm{d}}}x +\int _{\{t_nu_0\ge \beta \}}F(\beta ){{\mathrm{d}}}x+o_n(1)\\&<\frac{1}{4}\Vert u_0\Vert ^2+\int _{\{u_0>\beta \}}\left[ \frac{1}{4}f(u_0)u_0 -F(u_0)\right] {{\mathrm{d}}}x+\int _{\{u_0>\beta \}}F(\beta ){{\mathrm{d}}}x\\&\le \frac{1}{4}\Vert u_0\Vert ^2+\int _{{\mathbb {R}}^3}\left[ \frac{1}{4}{\underline{f}}_{H}(u_0)u_0 -F_{H}(u_0)\right] {{\mathrm{d}}}x+\int _{\{u_0\le \beta \}}F_H(u_0){{\mathrm{d}}}x\\&\le \liminf \limits _{n\rightarrow \infty }\bigg \{\frac{1}{4}\Vert u_n\Vert ^2 +\int _{{\mathbb {R}}^3}\left[ \frac{1}{4}{\underline{f}}_{H}(u_n)u_n-F_{H}(u_n)\right] {{\mathrm{d}}}x\bigg \}\\&\le \liminf \limits _{n\rightarrow \infty }[I_\beta (u_n) -\frac{1}{4}\langle \omega _n, u_n\rangle ]\\&<c_\beta , \end{aligned} \end{aligned}$$

(3.30)

which is a contradiction. Here, $\omega _n$ has been defined in Lemma 3.2. We conclude that Case 2 does not occur. The proof is complete. $\square$

4 Existence and concentration of positive solutions to ($\hbox {K}_\varepsilon$)

Let us consider the following Hilbert space

$$\begin{aligned} E_\varepsilon :=\bigg \{u\in H^\alpha ({\mathbb {R}}^3):\,\,\int _{{\mathbb {R}}^3}V(\varepsilon x)u^2{{\mathrm{d}}}x<\infty \bigg \} \end{aligned}$$

endowed with the norm

$$\begin{aligned} \Vert u\Vert _\varepsilon ^2=\int _{{\mathbb {R}}^3}[a|(-\Delta )^{\frac{\alpha }{2}}u|^2+V(\varepsilon x)u^2]{{\mathrm{d}}}x. \end{aligned}$$

The energy functional associated with ($\hbox {K}_\varepsilon$) is given by

$$\begin{aligned} I_{\varepsilon ,\beta }(u)=\frac{1}{2}\Vert u\Vert _\varepsilon ^2+\frac{b}{4} \left( \int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}}x\right) ^2-\int _{{\mathbb {R}}^3}F_H(u){{\mathrm{d}}}x,\quad u\in E_\varepsilon . \end{aligned}$$

Using the same argument as Lemma 3.1, we can prove that $I_{\varepsilon ,\beta }$ has the corresponding mountain pass geometry. The mountain pass level of $I_{\varepsilon ,\beta }$ is denoted by $c_{\varepsilon ,\beta }$, where is defined by

$$\begin{aligned} c_{\varepsilon ,\beta }:= \inf \limits _{\gamma \in \Gamma _\varepsilon } \max \limits _{s\in [0,1]}I_{\varepsilon ,\beta }{(\gamma (s))}>0, \end{aligned}$$

where

$$\begin{aligned} \Gamma _\varepsilon :=\{\gamma \in C([0,1],E_\varepsilon )\,\, |\,\,\gamma (0)=0,\, I_{\varepsilon ,\beta }(\gamma (1))<0\}. \end{aligned}$$

4.1 Existence

Define $I_{V_0}: H^\alpha ({\mathbb {R}}^3):\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} I_{V_0}(u):=\frac{1}{2}\int _{{\mathbb {R}}^3}(a|(-\Delta )^{\frac{\alpha }{2}}u|^2+{V_0} u^2){{\mathrm{d}}}x+\frac{b}{4}\left( \int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}}x\right) ^2-\int _{{\mathbb {R}}^3}F(u){{\mathrm{d}}}x, \end{aligned}$$

where ${V_0}\in (0,V_\infty )$. There exists a positive function $v\in H^\alpha ({\mathbb {R}}^3)$ (see [31]) such that $I'_{V_0}(v)=0$ and $I_{V_0}(v)=c_{V_0}$, where $c_{V_0}$ is the mountain pass level. Define the corresponding manifold of $I_{V_0}$ by

$$\begin{aligned} {\mathcal {N}}_{V_0}:=\{u\in H^\alpha ({\mathbb {R}}^3):\,\,I'_{V_0}(u)u=0\}, \end{aligned}$$

then $c_{V_0}=\inf _{u\in {\mathcal {N}}_{V_0}}I_{V_0}(u)$. For any $R>0$, let $\varphi _R\in C_0^\infty ({\mathbb {R}}^3)$ be such that $\varphi _R(x)=1$ in $B_R(0)$ and $\varphi _R(x)=0$ in ${\mathbb {R}}^3\setminus \{B_{2R}(0)\}$, with $0 \le \varphi _R\le 1$ and $|\nabla \varphi _R|\le \frac{C}{R}$ , where C is a constant independent of R. Denote by $v_R$ the function

$$\begin{aligned} v_{R}(x):=\varphi _R(x)v(x). \end{aligned}$$

It is not hard to show that

$$\begin{aligned} v_{R}\rightarrow v\quad \text {in}\quad H^\alpha ({\mathbb {R}}^3)\quad \quad \text {as}\quad R\rightarrow +\infty . \end{aligned}$$

For each $R>0$, there exists $t_{R}>0$ such that

$$\begin{aligned} I_{V_0}(t_{R}v_R)=\max \limits _{t\ge 0}I_{V_0}(tv_R). \end{aligned}$$

Thus, $I'_{V_0}(t_{R}v_R)=0$ and

$$\begin{aligned} \begin{aligned}&\frac{1}{t^2_{R}}\int _{{\mathbb {R}}^3}(|(-\Delta )^{\frac{\alpha }{2}} v_R|^2 +{V_0} v^2_R){{\mathrm{d}}}x +b\left( \int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}v_R|^2{{\mathrm{d}}}x\right) ^2\\&\quad =\int _{{\mathbb {R}}^3}\frac{f(t_{R}v_R)}{t^3_{R}v_R^3}v_R^4{{\mathrm{d}}}x, \end{aligned} \end{aligned}$$

(4.1)

which implies by $I'_{V_0}(v)=0$ that $t_{R}\rightarrow 1$ as $R\rightarrow \infty$. Thus, it is obvious that $t_{R}v_R\rightarrow v$ in $H^\alpha ({\mathbb {R}}^3)$ as $R\rightarrow \infty$. It then follows from $c_{V_0}<c_\infty$ that there exist $\delta>0, R>0$ such that

$$\begin{aligned} c_{V_0}+\delta<c_\infty \quad \text {and}\quad I_{V_0}(t_{R}v_R)<c_{V_0}+\frac{\delta }{2}. \end{aligned}$$

(4.2)

Similarly to Lemma 3.1, there exists $t_*>0$ such that $I_{\varepsilon ,\beta }(t_*t_{R}v_R)<0$ uniformly for $\varepsilon ,\beta >0$ small enough. Let us consider $\gamma (t)=tt_*t_{R}v_R$ for $t\in [0,1]$, and then $\gamma \in \Gamma _\varepsilon$. By the definition of $c_{\varepsilon ,\beta }$, we have

$$\begin{aligned} c_{\varepsilon ,\beta }\le \max \limits _{t\in [0,1]}I_{\varepsilon ,\beta }(\gamma (t)) =\max \limits _{t\ge 0}I_{\varepsilon ,\beta }(tt_{R}v_R) =I_{\varepsilon ,\beta }({\bar{t}}t_{R}v_R) \end{aligned}$$

(4.3)

for some ${\bar{t}}>0$ which depends on parameters $\varepsilon ,\beta ,R$. It is easy to prove that for each $R>0$ given, there exist positive constants $C_1,C_2>0$ such that $C_1<{\bar{t}}<C_2$ for $\varepsilon ,\beta >0$ small enough. Without loss of generality, we assume that $V(0)=V_0$. For any $\sigma >0$, there exists $\varepsilon _0>0$ such that

$$\begin{aligned} 0\le V(\varepsilon x)-V_0<\sigma \end{aligned}$$

for all $\varepsilon \in (0,\varepsilon _0)$ and $x\in B_{2R}(0)$. It then follows that

$$\begin{aligned} \int _{{\mathbb {R}}^3}V(\varepsilon x)(t_{R}v_R)^2{{\mathrm{d}}}x<\int _{{\mathbb {R}}^3}(V_0+\sigma )(t_{R}v_R)^2{{\mathrm{d}}}x. \end{aligned}$$

By virtue of the above facts, from ($f_1$)-($f_3$), we deduce that there exist $C_3,C_4>0$ such that

$$\begin{aligned} \begin{aligned} c_{\varepsilon ,\beta }&\le I_{V_0}(tt_{R}v_R)+\frac{\sigma }{2}\int _{{\mathbb {R}}^3}(t_{R}v_R)^2{{\mathrm{d}}}x\\&\quad +\int _{B_{2R}\cap \{t_{R}v_R\le \beta \}}F(t_{R}v_R){{\mathrm{d}}}x +\int _{B_{2R}\cap \{t_{R}v_R>\beta \}}F(\beta ){{\mathrm{d}}}x\\&\le c_{V_0}+C_R\sigma +{\bar{C}}_R\beta ^4, \end{aligned} \end{aligned}$$

(4.4)

where $C_R,{\bar{C}}_R$ are independent of $\varepsilon ,\beta$. Thus, there exist $\sigma , \beta ^*>0$ small enough that

$$\begin{aligned} (1+\beta ^2)c_{\varepsilon ,\beta }\le (1+\beta ^2)[c_{V_0}+C_R\sigma +{\bar{C}}_R\beta ^4]<c_\infty \end{aligned}$$

for any $\beta \in (0, \beta ^*)$. Therefore, it follows from Lemma 3.6 that ($\hbox {K}_\varepsilon$) has a non-trivial solution $u_{\varepsilon ,\beta }\in H^\alpha ({\mathbb {R}}^3)$ for $\varepsilon ,\beta >0$ small enough. Moreover, $I_{\varepsilon ,\beta }(u_{\varepsilon ,\beta })=c_{\varepsilon ,\beta }$. $\square$

4.2 Concentration

Assume that $u_{\varepsilon ,\beta }$ is the solution of equation ($\hbox {K}_\varepsilon$) obtained above. Then, there exists $\rho _{\varepsilon ,\beta }\in L^{\frac{p+1}{p}}({\mathbb {R}}^3)$ such that $u_{\varepsilon ,\beta }$ solves

$$\begin{aligned} \left\{ \begin{array}{ll} \left( a+b\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}u|^2{{\mathrm{d}}} x\right) (-\Delta )^\alpha {u}+V(\varepsilon x)u =\rho _{\varepsilon ,\beta } &{} \quad \text{ a. } \text{ e. } \text{ in }\,\,{\mathbb {R}}^3, \\ u\in H^\alpha ({\mathbb {R}}^3),\quad u>0 &{} \quad \text{ in }\,\, {\mathbb {R}}^3 \end{array} \right. \end{aligned}$$

(4.5)

with $\rho _{\varepsilon ,\beta }\in [{\underline{f}}_H(u_{\varepsilon ,\beta }),{\overline{f}}_H(u_{\varepsilon ,\beta })]$ a.e. in ${\mathbb {R}}^3$. Take $\varepsilon _n,\beta _n\rightarrow 0$ arbitrarily, we denote by $u_n=u_{\varepsilon _n,\beta _n}$ and $\rho _n=\rho _{\varepsilon _n,\beta _n}$.

It is important to compare the minimax levels $c_{V_0}$ and $c_{\varepsilon _n,\beta _n}$ in our arguments.

Lemma 4.1

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }c_{\varepsilon _n,\beta _n}=c_{V_0}>0. \end{aligned}$$

Proof

Due to the arbitrariness of $\sigma$ in (4.4), we deduce immediately that $\limsup _{n\rightarrow \infty }c_{\varepsilon _n,\beta _n}\le c_{V_0}$. Now it suffices to verify that

$$\begin{aligned} \liminf _{n\rightarrow \infty }c_{\varepsilon _n,\beta _n}\ge c_{V_0}. \end{aligned}$$

(4.6)

In fact, we assume on the contrary that there exist positive integer N large and $\delta >0$ small such that $c_{\varepsilon _n,\beta _n}\le c_{V_0}-\delta$ for all $n>N$. From Lemma 3.6 and the definition of $c_{\varepsilon _n,\beta _n}$, we have

$$\begin{aligned} c_{\varepsilon _n,\beta _n}=I_{\varepsilon _n,\beta _n}(u_{\varepsilon _n,\beta _n}) =\max _{h>0}I_{\varepsilon _n,\beta _n}(hu_{\varepsilon _n,\beta _n})<c_{V_0}-\delta \end{aligned}$$

for any fixed $n>N$. Again by the definition of $c_{V_0}$, we know that $c_{V_0}\le \max _{h>0}I_{V_0}(hu_{\varepsilon _n,\beta _n})$. It follows from the fact that $V_0\le V(\varepsilon _n x)$ for all given $n> N$ and $x\in {\mathbb {R}}^3$ that

$$\begin{aligned} c_{V_0}-\delta>\max _{h>0}I_{\varepsilon _n,\beta _n}(hu_{\varepsilon _n,\beta _n}) \ge \max _{h>0}I_{V_0}(hu_{\varepsilon _n,\beta _n})\ge c_{V_0}, \end{aligned}$$

which is a contradiction. Thus, (4.6) holds and the proof is complete. $\square$

Lemma 4.2

There exist a sequence $\{y_n\}\subset {\mathbb {R}}^3$ and constants $R,\tau >0$ such that

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\int _{B_R(y_n)}u_n^2{{\mathrm{d}}}x\ge \tau >0. \end{aligned}$$

Proof

Suppose on the contrary that the conclusion does not hold. Using the similar arguments as in Lemma 3.2, we have that $\{u_n\}$ is bounded in $H^\alpha ({\mathbb {R}}^3)$. It then follows from Lemma 2.4 that $u_n\rightarrow 0$ in $L^s({\mathbb {R}}^3)$ for $s\in (2, 2_\alpha ^*)$. By virtue of ($f_1$) and ($f_2$), for any $\varepsilon >0$, there exists $C_\varepsilon >0$ such that $f(u_n)\le \varepsilon |u_n|+C_\varepsilon |u_n|^p$. So from the definition of $F_{H}$ and the fact that $\rho _{n}\in [{\underline{f}}_H(u_{n}),{\overline{f}}_H(u_{n})]$ a.e. in ${\mathbb {R}}^3$, we deduce that $\int _{{\mathbb {R}}^3}F_H(u_n){{\mathrm{d}}}x\rightarrow 0$ and $\int _{{\mathbb {R}}^3}\rho _{n}u_n{{\mathrm{d}}}x\rightarrow 0$ as $n\rightarrow \infty$. It follows that

$$\begin{aligned} \begin{aligned} o(1)&=\Vert u_n\Vert _{\varepsilon _n}^2+\Vert u_n\Vert _{D^{\alpha ,2}}^4,\\ c_{\varepsilon _n,\beta _n}+o(1)&=\frac{1}{2}\Vert u_n\Vert _{\varepsilon _n}^2 +\frac{1}{4}\Vert u_n\Vert _{D^{\alpha ,2}}^4, \end{aligned} \end{aligned}$$

which contradicts Lemma 4.1. The proof is complete. $\square$

It is known that $\{u_n\}$ is bounded in $H^\alpha ({\mathbb {R}}^3)$. Take $v_n:=u_n(x+{\tilde{y}}_n)$ such that $v_n\rightharpoonup v\ne 0$ in $H^\alpha ({\mathbb {R}}^3)$ and $v_n(x)\rightarrow v(x)$ a.e., in ${\mathbb {R}}^3$. Then, $v_n$ solves the following equation

$$\begin{aligned} \left\{ \begin{array}{ll} \left( a+b\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}v_n|^2{{\mathrm{d}}}x \right) (-\Delta )^\alpha {v_n}+V_n(x)v_n ={\tilde{\rho }}_{n} &{} \quad \text{ a. } \text{ e. } \text{ in }\,\,{\mathbb {R}}^3, \\ v_n\in H^\alpha ({\mathbb {R}}^3),\quad v_n>0 &{} \quad \text{ in }\,\, {\mathbb {R}}^3 \end{array} \right. \end{aligned}$$

(4.7)

with $V_n(x)=V(\varepsilon _n x+\varepsilon _n {\tilde{y}}_n)$ and ${\tilde{\rho }}_{n}(x)\in [{\underline{f}}_H(v_{n}(x)), {\overline{f}}_H(v_{n}(x))]$ a.e. in ${\mathbb {R}}^3$.

Lemma 4.3

$\{v_n\}$ has a convergent subsequence in $H^\alpha ({\mathbb {R}}^3)$. Moreover, up to a subsequence, $y_n:=\varepsilon _n{\tilde{y}}_{\varepsilon _n}\rightarrow y^*\in \Theta$, where $\Theta :=\{x\in {\mathbb {R}}^3| V(x)=V_0\}$.

Proof

For each $v_n$, choosing $t_n>0$ such that ${\bar{v}}_n:=t_nv_n\in {\mathcal {N}}_{V_0}$, we deduce from $0\in \partial I_{\varepsilon _n,\eta _n}(u_n)$ and Lemma 3.6 that

$$\begin{aligned} \begin{aligned} I_{V_0}(t_nv_n)&\le \frac{t_n^2}{2}\int _{{\mathbb {R}}^3}a|(-\Delta )^{\alpha /2} v_n|^2 +V_n(x)v_n^2){{\mathrm{d}}}x+\frac{t_n^4}{4}b\left( \int _{{\mathbb {R}}^3}| (-\Delta )^{\frac{\alpha }{2}}v_n|^2{{\mathrm{d}}}x\right) ^2 -\int _{{\mathbb {R}}^3} F_H(t_nv_n){{\mathrm{d}}}x\\&=I_{\varepsilon _n,\eta _n}(t_nu_n) \le I_{\varepsilon _n,\eta _n}(u_n)=c_{V_0}+o(1). \end{aligned} \end{aligned}$$

So, it follows from $I_{V_0}({\bar{v}}_n)\ge c_{V_0}$ that $\lim _{n\rightarrow \infty }I_{V_0}({\bar{v}}_n)=c_{V_0}$. We can show that $\{t_n\}$ is bounded. Indeed, since $\Vert u_n\Vert _{\varepsilon _n}^2$ is bounded uniformly for n, we can easy obtain $I_{V_0}({\bar{v}}_n)\rightarrow -\infty$ when $t_n\rightarrow +\infty$. This is not possible since $I_{V_0}({\bar{v}}_n)\ge c_{V_0}$ for all $n\in {\mathbb {N}}$. Hence, $\{t_n\}$ is bounded. Up to subsequence, we assume that $t_n\rightarrow t\ge 0$. If $t=0$, then ${\bar{v}}_n\rightarrow 0$ in $H^\alpha ({\mathbb {R}}^3)$, because $\{v_n\}$ is bounded in $H^\alpha ({\mathbb {R}}^3)$. Hence, $I_{V_0}({\bar{v}}_n)\rightarrow 0$ as $n\rightarrow \infty$, which contradicts $c_{V_0}>0$. So ${\bar{v}}_n:=t_nv_n\rightharpoonup {\bar{v}}$ in $H^\alpha ({\mathbb {R}}^3)\setminus {\{0\}}$. By uniqueness, we deduce ${\bar{v}}=tv$. Using Ekeland’s variational principle in [19], we can prove that $\{{\bar{v}}_n\}\subset {\mathcal {N}}_{V_0}$ is a Palais–Smale sequence of $I_{V_0}$ (see Lemma 5.1 in [32]), that is,

$$\begin{aligned} I_{V_0}({\bar{v}}_n)\rightarrow c_{V_0}\quad I'_{V_0}({\bar{v}}_n)\rightarrow 0\quad \text {in}\,\,H^\alpha ({\mathbb {R}}^3). \end{aligned}$$

(4.8)

Although $I_{V_0}$ is of $C^1$ class, we can still use the similar arguments as in Lemma 3.6 to obtain ${\bar{v}}_n\rightarrow {\bar{v}}$ in $H^\alpha ({\mathbb {R}}^3)$ and ${\bar{v}}\in {\mathcal {N}}_{V_0}$, and so $v_n\rightarrow v$ in $H^\alpha ({\mathbb {R}}^3)$. Let us show that $y_n:=\varepsilon _n{\tilde{y}}_n$ is bounded. If not, then $|y_n|\rightarrow \infty$. It follows from ${\bar{v}}_n\in {\mathcal {N}}_{V_0}$, the Fatou Lemma and Lemma 3.6 that

$$\begin{aligned} \begin{aligned} c_{V_0}&\le I_{V_0}({\bar{v}}) < I_{V_\infty }(tv)-\frac{1}{4}I'_{V_0}(tv)tv\\&=\int _{{\mathbb {R}}^3}\left[ \frac{a}{4}|(-\Delta )^{\alpha /2} tv|^2 +\left( \frac{1}{2}V_\infty -\frac{1}{4}V_0\right) t^2v^2\right] {{\mathrm{d}}}x+\int _{{\mathbb {R}}^3} \left( f(tv)tv-\frac{1}{4}F(tv)\right) {{\mathrm{d}}}x\\&\le \liminf \limits _{n\rightarrow \infty }\bigg (\frac{1}{4}\int _{{\mathbb {R}}^3}| (-\Delta )^{\alpha /2} t_nv_n|^2{{\mathrm{d}}}x+\int _{{\mathbb {R}}^3}\left( \frac{1}{2}V (\varepsilon _n x+y_n)-\frac{1}{4}V_0\right) t_n^2v_n^2{{\mathrm{d}}}x\\&\quad +\int _{{\mathbb {R}}^3} (f(t_nv_n)t_nv_n-\frac{1}{4}F_H(t_nv_n)){{\mathrm{d}}}x\bigg )\\&=\liminf \limits _{n\rightarrow \infty }I_{\varepsilon _n,\beta _n}(t_nu_n) \le \liminf \limits _{n\rightarrow \infty }I_{\varepsilon _n,\beta _n}(u_n)=c_{V_0}, \end{aligned} \end{aligned}$$

which is a contradiction. So $\{y_n\}$ is bounded. Up to subsequence, $y_n\rightarrow y^*$. Moreover, since $f(t)=0$ for all $t\le 0$, we have as $\beta \rightarrow 0$

$$\begin{aligned} {\underline{f}}_{H}(t),\,{\overline{f}}_{H}(t)\rightarrow \left\{ \begin{array}{ll} 0, &{} \quad \text{ if }\,\,t<0, \\ f(t), &{} \quad \text{ if }\,\, t\ge 0. \end{array} \right. \end{aligned}$$

Hence, based on the facts that ${\tilde{\rho }}_{n}(x)\in [{\underline{f}}_H(v_{n}(x)), {\overline{f}}_H(v_{n}(x))]$ a.e. in ${\mathbb {R}}^3$ and $v_n\rightarrow v$ in $H^\alpha ({\mathbb {R}}^3)$, using the Lebesgue dominated convergence theorem, we deduce that for any $\eta \in C_0^\infty ({\mathbb {R}}^3)$

$$\begin{aligned} \int _{{\mathbb {R}}^3} {\tilde{\rho }}_{n}\eta {{\mathrm{d}}}x\rightarrow \int _{{\mathbb {R}}^3} f(v)\eta {{\mathrm{d}}}x,\quad \text {as}\,\,n\rightarrow \infty . \end{aligned}$$

For each $\eta \in C_0^\infty ({\mathbb {R}}^3)$, we then deduce from (4.7) and $v_n\rightarrow v$ in $H^\alpha ({\mathbb {R}}^3)$ that

$$\begin{aligned} \begin{aligned}&\lim \limits _{n\rightarrow \infty }\bigg ((a+b\Vert v_n\Vert _{D^{\alpha ,2}}^2) \int _{{\mathbb {R}}^3}(-\Delta )^{\alpha /2}v_n (-\Delta )^{\alpha /2}\eta {{\mathrm{d}}}x+\int _{{\mathbb {R}}^3} V_n(x)v_n\eta {{\mathrm{d}}}x-\int _{{\mathbb {R}}^3} {\tilde{\rho }}_{n}\eta {{\mathrm{d}}}x\bigg )\\&\quad =(a+b\Vert v\Vert _{D^{\alpha ,2}}^2)\int _{{\mathbb {R}}^3}(-\Delta )^{\alpha /2}v (-\Delta )^{\alpha /2}\eta {{\mathrm{d}}}x+\int _{{\mathbb {R}}^3} V(y^*)v\eta {{\mathrm{d}}}x-\int _{{\mathbb {R}}^3} f(v)\eta {{\mathrm{d}}}x. \end{aligned} \end{aligned}$$

Therefore, the limit v of sequence $\{v_n\}$ solves the equation

$$\begin{aligned} (a+b\Vert v\Vert _{D^{\alpha ,2}}^2)(-\Delta )^\alpha v+V(y^*)v=f(v) \quad \text{ in }\,{\mathbb {R}}^3. \end{aligned}$$

(4.9)

Define the functional

$$\begin{aligned} I_{y^*}(u):=\frac{1}{2}\int _{{\mathbb {R}}^3}(a|(-\Delta )^{\alpha /2} u|^2+V(y^*)u^2){{\mathrm{d}}}x+ \frac{b}{4}\Vert v\Vert _{D^{\alpha ,2}}^4 -\int _{{\mathbb {R}}^3} F(u){{\mathrm{d}}}x. \end{aligned}$$

If $V(y^*)>V_0$, then we can get a contradiction by similar arguments as above. So $V(y^*)=V_0$ and $I_{y^*}(v)=c_{V_0}$. That is to say, v is a positive ground state solutions of (4.9). The proof is complete. $\square$

We use the Moser iteration method [36] to prove $L^\infty$-estimate for problem (4.7).

Lemma 4.4

Let $u_n\in E_{\varepsilon _n}$ be a solution of problem ($\hbox {K}_{\varepsilon _n}$) with $\varepsilon _n\rightarrow 0^+$ and $\beta _n\rightarrow 0$. Then, $v_n=u_n(\cdot +{\tilde{y}}_n)\in L^\infty ({\mathbb {R}}^3)$ uniformly for n.

Proof

Since $|\Lambda ^*|=0$ with $\Lambda ^*:=\{x\in {\mathbb {R}}^3\,|\, v_n(x)=\beta \}$, our argument is similar to that in Lemma 3.2 of [6]. So we omit the details of the proof. $\square$

Now, we claim that there exists $c > 0$ such that $\Vert v_n\Vert _\infty \ge c>0$. Otherwise, $\Vert v_n\Vert _\infty \rightarrow 0$ as $n\rightarrow \infty$. By ($f_1$)-($f_3$) and the definition of $f_H$, for n large enough, we have

$$\begin{aligned} \int _{{\mathbb {R}}^3}[a|(-\Delta )^{\alpha /2} v_n|^2+V_0v_n^2]{{\mathrm{d}}}x \le \int _{{\mathbb {R}}^3}\frac{ V_0}{2}v_n^2{{\mathrm{d}}}x, \end{aligned}$$

which is a contradiction. Hence, from Lemma 4.4 there exist $c,C>0$ independent of n such that

$$\begin{aligned} c\le \Vert v_n\Vert _\infty \le C. \end{aligned}$$

(4.10)

Observe from (4.7) that $v_n$ solves

$$\begin{aligned} \left\{ \begin{array}{ll} (-\Delta )^\alpha {v_n}+v_n=\chi _n &{} \quad \text{ a. } \text{ e. } \text{ in }\,\,{\mathbb {R}}^3, \\ v_n\in H^\alpha ({\mathbb {R}}^3),\quad v_n>0 &{} \quad \text{ in }\,\, {\mathbb {R}}^3, \end{array} \right. \end{aligned}$$

(4.11)

where

$$\begin{aligned} \chi _n(x):=\left( a+b\int _{{\mathbb {R}}^3}|(-\Delta )^{\frac{\alpha }{2}}v_n|^2{{\mathrm{d}}}x\right) ^{-1}[{\tilde{\rho }}_n-V_n(x)v_n]+v_n \end{aligned}$$

and $V_n(x)=V(\varepsilon _n x+\varepsilon _n {\tilde{y}}_n)$ and ${\tilde{\rho }}_{n}(x)\in [{\underline{f}}_H(v_{n}(x)),{\overline{f}}_H(v_{n}(x))]$ a.e. in ${\mathbb {R}}^3$. From (4.10) and the definitions of ${\underline{f}}_H, {\overline{f}}_H$, we deduce that $\{{\tilde{\rho }}_{n}\}$ is bounded in $L^\infty ({\mathbb {R}}^3)$. Using the fact that $v_n\rightarrow v$ in $H^\alpha ({\mathbb {R}}^3)$, we see that there exists ${\tilde{\rho }}^*(x)\in [{\underline{f}}_H(v(x)),{\overline{f}}_H(v(x))]$ a.e. in ${\mathbb {R}}^3$, such that ${\tilde{\rho }}_{n}\rightarrow {\tilde{\rho }}^*$ in $L^{\frac{p+1}{p}}({\mathbb {R}}^3)$, and then ${\tilde{\rho }}_{n}\rightarrow {\tilde{\rho }}^*$ in $L^{s}({\mathbb {R}}^3)$ for $s\in [\frac{p+1}{p},\infty )$. Hence, there exists $\chi \in L^q({\mathbb {R}}^3)$ such that

$$\begin{aligned} \chi _n\rightarrow \chi \quad \text {in}\,\,L^q({\mathbb {R}}^3)\quad \quad \forall q\in [2,+\infty ), \end{aligned}$$

and there exits $C>0$ independent of n such that $\Vert \chi _n\Vert _\infty \le C$. Based on the above, $v_{n}$ can be expressed as

$$\begin{aligned} v_n(x):=({\mathcal {K}}*\chi _n)(x)=\int _{{\mathbb {R}}^3}{\mathcal {K}}(x-z)\chi _n(z)dz, \end{aligned}$$

where ${\mathcal {K}}$ is the Bessel kernel and satisfies the following properties (see [20]):

• (1) ${\mathcal {K}}$ is positive, radially symmetric and smooth in ${\mathbb {R}}^3\setminus \{0\}$,

• (2) there is $C>0$ such that ${\mathcal {K}}(x)\le \frac{C}{|x|^{3+2\alpha }}$ for any $x\in {\mathbb {R}}^3\setminus \{0\}$,

• (3) ${\mathcal {K}}\in L^{r}({\mathbb {R}}^3)$ for any $r\in [1,\frac{3}{3-2\alpha })$.

Arguing as in Theorem 3.4 in [20], we have that

$$\begin{aligned} v_n(x)\rightarrow 0\quad \text {as}\,\,|x|\rightarrow \infty \,\,\text {uniformly in }n\in {\mathbb {N}}. \end{aligned}$$

For $c>0$ given in (4.10), we can find $R>0$ such that $v_n(x)<c$ for all $|x|\ge R$ and uniformly for $n\in {\mathbb {N}}$. Let $x_n$ denote the maximum point of $v_n$, then $|x_n|\le R$. Moreover, we have $z_n=x_n+{\tilde{y}}_n$ where $z_n$ is one maximum point of $v_n$. It is easy to check from Lemma 4.3 that

$$\begin{aligned} \varepsilon _nz_n=\varepsilon _nx_n+\varepsilon _n{\tilde{y}}_n\rightarrow y^*\in \Theta . \end{aligned}$$

By the continuity of V, we obtain

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }V(\varepsilon _nz_n)=V(y^*)=V_0. \end{aligned}$$

The proof is complete. $\square$