Abstract
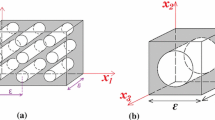
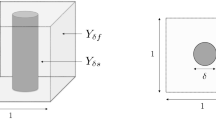
We study the asymptotic behavior of a fluid flow in a thin porous medium of thickness \(\varepsilon \), which is characteristic size of the pores \(\varepsilon \) and contains a fissure of width \(\eta _\varepsilon \). We consider the limit when the size of the pores tends to zero, and we find a critical size \(\eta _\varepsilon \approx \varepsilon ^{2\over 3}\) in which the flow is described by a 2D Darcy law coupled with a 1D Reynolds problem. We also discuss the other cases.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Allaire, G.: Homogenization of the Stokes flow in a connected porous medium. Asymptot. Anal. 2, 203–222 (1989)
Allaire, G.: Homogenization and two-scale convergence. SIAM J. Math. Anal. 23, 1482–1518 (1992)
Anguiano, M.: Darcy’s laws for non-stationary viscous fluid flow in a thin porous medium. Math. Methods Appl. Sci. (2016). doi:10.1002/mma.4204
Bourgeat, A., ElAmri, H., Tapiero, R.: Existence d’une taille critique pour une fissure dans un milieu poreux. Second Colloque Franco Chilien de Mathematiques Appliquées, Cepadués Edts, Tolouse, pp. 67–80 (1991)
Bourgeat, A., Tapiero, R.: Homogenization in a perforated domain including a thin full interlayer. Int. Ser. Numer. Math. 114, 25–36 (1993)
Bourgeat, A., Marušic-Paloka, E., Mikelić, A.: Effective fluid flow in a porous medium containing a thin fissure. Asymptot. Anal. 11, 241–262 (1995)
Bourgeat, A., Mikelić, A.: Homogenization of a polymer flow through a porous medium. Nonlinear Anal. 26, 1221–1253 (1996)
Ciarlet, P.G., Ledret, H., Nzwenga, R.: Modélisation de la jonction entre un corps élastique tridimensionnel et une plaque. C. R. Acad. Sci. Paris Ser. I(305), 55–58 (1987)
Nguetseng, G.: A general convergence result for a functional related to the theory of homogenization. SIAM J. Math. Anal. 20, 608–623 (1989)
Panasenko, G.P.: Higher order asymptotics of solutions of problems on the contact of periodic structures. Math. U.S.S.R. Sbornik 38, 465–494 (1981)
Sanchez-Palencia, E.: Non-homogeneous media and vibration theory. In: Ehlers, J., Hepp, K., Kippenhahn, R., Weidenmüller, H.A., Zittartz, J. (eds.) Lecture Notes in Physics. Springer, Berlin/Heidelberg/New York (1980)
Tartar, L.: Incompressible fluid flow in a porous medium convergence of the homogenization process. In: Ehlers, J., Hepp, K., Kippenhahn, R., Weidenmüller, H.A., Zittartz, J. (eds.) Appendix to Lecture Notes in Physics, vol. 127. Springer, Berlin (1980)
Temam, R.: Navier–Stokes equations and nonlinear functional analysis. In: CBMS-NSF Regional Conference Series in Applied Mathematics, vol. 41. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (1983)
Zhao, H., Yao, Z.: Effective models of the Navier–Stokes flow in porous media with a thin fissure. J. Math. Anal. Appl. 387, 542–555 (2012)
Author information
Authors and Affiliations
Corresponding author
Additional information
María Anguiano has been supported by Junta de Andalucía (Spain), Proyecto de Excelencia P12-FQM-2466, and in part by European Commission, Excellent Science-European Research Council (ERC) H2020-EU.1.1.-639227. Francisco Javier Suárez-Grau has been supported by Ministerio de Economía y Competitividad (Spain), Proyecto Excelencia MTM2014-53309-P.
Rights and permissions
About this article
Cite this article
Anguiano, M., Suárez-Grau, F.J. Derivation of a coupled Darcy–Reynolds equation for a fluid flow in a thin porous medium including a fissure. Z. Angew. Math. Phys. 68, 52 (2017). https://doi.org/10.1007/s00033-017-0797-5
Received:
Revised:
Published:
DOI: https://doi.org/10.1007/s00033-017-0797-5