Skip to main content
SpringerLink
Log in

Discrete Sommerfeld diffraction problems on hexagonal lattice with a zigzag semi-infinite crack and rigid constraint

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

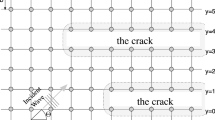
Diffraction problems, associated with waves scattered by a semi-infinite crack and rigid constraint, in a hexagonal (honeycomb) lattice model, with nearest neighbor interactions, are solved exactly using the method of Wiener and Hopf. Asymptotic expressions for the scattered waves in far field are provided for both problems, by application of the method of stationary phase to corresponding diffraction integrals. Additionally, for the crack diffraction problem, bond lengths on the semi-infinite row complementing the crack, as well as the crack opening displacement, are provided in closed form except for the presence of concomitant Fourier coefficients of the Wiener–Hopf kernel. For the rigid constraint diffraction problem, the solution on the semi-infinite row complementing the constrained lattice sites, as well as that adjacent to the constrained row, are provided in similar closed form. The amplitude, as well as phase, of waves in far field is compared, through graphical plots, with that of a numerical solution on finite grid. Also, the analytical solution for few sites near the tip of each defect is compared with numerical solution. Both discrete Sommerfeld diffraction problems and their solutions are also relevant to numerical solution of the two-dimensional Helmholtz equation using a 4-point hexagonal grid, besides having applications inherent to the scattering of waves on a honeycomb structure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ablowitz M.J., Fokas A.S.: Complex Variables: Introduction and Applications. Cambridge University Press, Cambridge (1997)

    MATH  Google Scholar 

  2. Ablowitz M.J., Zhu Y.: Nonlinear waves in shallow honeycomb lattices. SIAM J. Appl. Math. 72(1), 240–260 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  3. Achenbach J.D.: Wave Propagation in Elastic Solids. North-Holland Publishing Company, Amsterdam (1973)

    MATH  Google Scholar 

  4. Al-Jishi R., Dresselhaus G.: Lattice-dynamical model for graphite. Phys. Rev. B 26, 4514–4522 (1982)

    Article  Google Scholar 

  5. Ando, K., Isozaki, H., Morioka, H.: Spectral properties of Schrödinger operators on perturbed lattices (2015). http://arxiv-web3.library.cornell.edu/pdf/1408.2076

  6. Berenger J.P.: A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 114, 185–200 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  7. Berry M.V., Jeffrey M.R.: Conical diffraction: Hamilton’s diabolical point at the heart of crystal optics. Prog Optics 50, 13–50 (2007)

    Article  Google Scholar 

  8. Bilbao S.: Wave and Scattering Methods for Numerical Simulation. Wiley, New York (2004)

    Book  Google Scholar 

  9. Born M., Wolf E.: Principles of Optics. Cambridge University Press, Cambridge (1999)

    Book  Google Scholar 

  10. Böttcher A., Silbermann B.: Analysis of Toeplitz Operators, 2nd edn. Springer, Cambridge (2006)

    MATH  Google Scholar 

  11. Brillouin L.: Wave Propagation in Periodic Structures; Electric Filters and Crystal Lattices. Dover Publications, New York (1953)

    MATH  Google Scholar 

  12. Capolino F., Albani M.: Truncation effects in a semi-infinite periodic array of thin strips: A discrete Wiener–Hopf formulation. Radio. Sci. 44, RS2S91 (2009)

    Article  Google Scholar 

  13. Collatz L.: The numerical treatment of differential equations, third edition edn. Springer, Berlin (1960)

    Book  Google Scholar 

  14. Dean P.: The vibrations of three two-dimensional lattices. Proc. Camb. Phil. Soc. 59, 383–396 (1963)

    Article  MATH  Google Scholar 

  15. Erdélyi A.: Asymptotic representations of Fourier integrals and the method of stationary phase. J. Soc. Ind. Appl. Math. 3(1), 17–27 (1955)

    Article  MATH  Google Scholar 

  16. Fefferman C.L., Weinstein M.I.: Honeycomb lattice potentials and Dirac points. J. Am. Math. Soc. 25, 1169–1220 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  17. Fefferman C.L., Weinstein M.I.: Wave packets in honeycomb structures and two-dimensional Dirac equations. Commun. Math. Phys. 326, 251–286 (2015)

    Article  MathSciNet  Google Scholar 

  18. Fel’d Y.N.: Diffraction of electromagnetic waves on a semi-infinite grating. Radiotekhn i Elektron 3, 882–884 (1958)

    Google Scholar 

  19. Felsen L.B., Marcuvitz N.: Radiation and Scattering of Waves. Prentice–Halls, Englewood Cliffs (1973)

    Google Scholar 

  20. Gohberg, I., Feldman, I.: Convolution Equations and Projection Methods for Their Solutions. Math. Monogr., 41, AMS, Providence RI (1974)

  21. Hackbusch W.: On the regularity of difference schemes. Arkiv fuer Matematik 19(1–2), 71–95 (1981)

    Article  MATH  MathSciNet  Google Scholar 

  22. Hahn T.: International Tables for Crystallography, Volume A: Space Group Symmetry, 5th edn. Springer, Berlin (2002)

    Google Scholar 

  23. Harris J.G.: Linear Elastic Waves. Cambridge University Press, Cambridge (2004)

    Google Scholar 

  24. Horiguchi T.: Lattice Green’s functions for the triangular and honeycomb lattices. J. Math. Phys. 13, 1411–1419 (1972)

    Article  MathSciNet  Google Scholar 

  25. Jones D.S.: A simplifying technique in the solution of a class of diffraction problems. Quart. J. Math. 3, 1952 (1952)

    Article  Google Scholar 

  26. Jones D.S.: The Theory of Electromagnetism. Macmillan, New York (1964)

    MATH  Google Scholar 

  27. Jury E.I.: Theory and Application of the z-Transform Method. Wiley, New York (1964)

    Google Scholar 

  28. Kantorovich, L., Krylov, V.: Approximate methods of higher analysis. Interscience Publishers, New York, translated by Curtis D. Benster (1958)

  29. Karp S.: Diffraction by finite and infinite gratings. Phys. Rev. 86, 586–601 (1952)

    Google Scholar 

  30. Krein M.G.: Integral equations on a half-line with kernel depending upon the difference of the arguments. Am. Math. Soc. Transl. Ser. 2 22, 163–288 (1962)

    MATH  Google Scholar 

  31. Lomer W.M.: The valence bands in two-dimensional graphite. Proc. Roy. Soc. A Math. Phys. Sci. 227, 330–349 (1955)

    Article  MATH  Google Scholar 

  32. Makwana M., Craster R.V.: Localised point defect states in asymptotic models of discrete lattices. Quart. Mech. Appl. Math. 66, 289–316 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  33. Marder M., Gross S.: Origin of crack tip instabilities. J. Mech. Phys. Solids 43(1), 1–48 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  34. Martin P.A.: Discrete scattering theory: Green’s function for a square lattice. Wave Motion 43, 619–629 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  35. Meyer, J.C., Kisielowski, C., Erni, R., Rossell, M.D., Crommie, M.F., Zettl, A.: Direct imaging of lattice atoms and topological defects in graphene membranes. Nano. Lett. 8(11), 3582–6 (2008)

  36. Michel K.H., Verberck B.: Theory of the evolution of phonon spectra and elastic constants from graphene to graphite. Phys. Rev. B 78(11), 085,424 (2008)

    Article  Google Scholar 

  37. Mikhlin S.G., Prößdorf S.: Singular integral operators. Springer, Basel (1986)

    Book  Google Scholar 

  38. Newell G.F.: Vibration spectrum of graphite and boron nitride I: The two-dimensional spectrum. J. Chem. Phys. 24, 1049–1060 (1956)

    Article  Google Scholar 

  39. Newell G.F.: Vibration spectrum of graphite and boron nitride II: The three-dimensional spectrum. J. Chem. Phys. 27, 240–250 (1957)

    Article  Google Scholar 

  40. Noble B.: Methods Based on the Wiener–Hopf Technique. Pergamon Press, London (1958)

    MATH  Google Scholar 

  41. Novoselov K.S.: Nobel lecture: Graphene: Materials in the flatland. Rev. Modern Phys. 83, 837–849 (2011)

    Article  Google Scholar 

  42. Paley R.E.A.C., Wiener N.: Fourier Transforms in the Complex Domain. American Mathematical Society, Providence (1934)

    MATH  Google Scholar 

  43. Rosenstock H.B.: Dynamics of the graphite lattice. J. Chem. Phys. 21, 2064–2069 (1953)

    Article  Google Scholar 

  44. Rutter G.M., Crain J.N., Guisinger N.P., Li T., First P.N., Stroscio J.A.: Scattering and interference in epitaxial graphene. Science 317, 219–222 (2007)

    Article  Google Scholar 

  45. Shaban W., Vainberg B.: Radiation conditions for the difference Schrödinger operators. Appl. Anal. 80, 525–556 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  46. Sharma, B.L.: Diffraction of waves on square lattice by semi-infinite crack. SIAM J. Appl. Math. 75(3), 1171–1192 (2015). doi:10.1137/140985093

  47. Sharma, B.L.: Diffraction of Waves on Square Lattice by Semi-infinite rigid constraint. Wave Motion (2015). doi:10.1016/j.wavemoti.2015.07.008

  48. Sharma, B.L.: Diffraction of waves on triangular lattice by a semi-infinite rigid constraint and crack. (submitted) pp 1–27 (2015c)

  49. Sharma, B.L.: Edge diffraction on triangular and hexagonal lattices: existence, uniqueness, and finite section. (submitted) pp 1–23 (2015d)

  50. Sharma, B.L.: Near-tip field for diffraction on square lattice by crack. SIAM J. Appl. Math. 75(4), 1915–1940 (2015). doi:10.1137/15M1010646

  51. Sharma, B.L.: Near-tip field for diffraction on square lattice by rigid constraint. Zeitschrift für Angewandte Mathematik und Physik pp 1–22, (2015f). doi:10.1007/s00033-015-0508-z

  52. Sherry P.B., Coulson C.A.: The vibrational frequency distribution of graphite: I. out-of-plane modes of a single layer. Proc. Phys. Soc. B 69, 1326–1330 (1956)

    Article  Google Scholar 

  53. Singer I., Turkel E.: A perfectly matched layer for the Helmholtz equation in a semi-infinite strip. J. Comput. Phys. 201, 439–465 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  54. Slepyan L.I.: Models and Phenomena in Fracture Mechanics. Springer, Berlin (2002)

    Book  MATH  Google Scholar 

  55. Sommerfeld A.: Mathematische theorie der diffraction. Math. Ann. 47(2-3), 317–374 (1896). doi:10.1007/BF01447273

  56. Sommerfield A.: Optics. Lectures on Theoretical Physics, Vol. IV. Academic Press, New York (1964)

    Google Scholar 

  57. Wallace P.R.: The band theory of graphite. Phys. Rev. B 71, 622–634 (1947)

    Article  MATH  Google Scholar 

  58. Wiener N., Hopf E.: Über eine klasse singulärer integralgleichungen. Sitzungsber Preuss Akad Wiss Berlin, Phys-Math 32, 696–706 (1931)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Indian Institute of Technology Kanpur, Kanpur, U. P, 208016, India

    Basant Lal Sharma

Authors
  1. Basant Lal Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Basant Lal Sharma.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sharma, B.L. Discrete Sommerfeld diffraction problems on hexagonal lattice with a zigzag semi-infinite crack and rigid constraint. Z. Angew. Math. Phys. 66, 3591–3625 (2015). https://doi.org/10.1007/s00033-015-0574-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00033-015-0574-2

Mathematics Subject Classification

Keywords

Search

Navigation