Bloch wave homogenization of a non-homogeneous Neumann problem

Abstract.

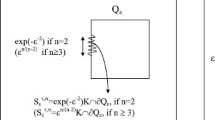
In this paper, we use the Bloch wave method to study the asymptotic behavior of the solution of the Laplace equation in a periodically perforated domain, under a non-homogeneous Neumann condition on the boundary of the holes, as the size of the holes goes to zero more rapidly than the domain period. This method allows to prove that, when the hole size exceeds a given threshold, the non-homogeneous boundary condition generates an additional term in the homogenized problem, commonly referred to as “the strange term” in the literature.