Abstract
We study the class of algebraic Lie algebras for which the generic stabilizer of the coadjoint action is reductive modulo the center.
Résumé
Nous étudions la classe des algèbres de Lie dont le stabilisateur générique de la représentation coadjointe est réductif modulo le centre.
Similar content being viewed by others
Références
M. Andler, La formule de Plancherel pour les groupes algébriques complexes unimodulaires, Acta. Math. 154 (1985), 1–104.
N. H. Anh, Algebraic groups with square-integrable representations, Bull. Amer. Math. Soc. 80 (1974), 539–542.
N. H. Anh, Classification of unimodular algebraic groups with square integrable representations, Acta Mathematica Vietnamica 3 (1978), no. 2, 75–81.
N. H. Anh, Classification of connected unimodular Lie groups with discrete series, Ann. Inst. Fourier, Grenoble 30 (1980), no. 1, 159–192.
A. Borel, Harish-Chandra, Arithmetic subroups of algebraic groups, Annals of Math. 75 (1962), 485–535.
K. Baur, A. Moreau, Quasi-reductive (bi)parabolic subalgebras in the reductive Lie algebras, Ann. Instit. Fourier (Grenoble) 61 (2011), no. 2, 417–451.
D. Burde, Characteristically nilpotent Lie algebras and symplectic structures, Forum Math. 18 (2006), no. 5, 769–787.
J.-Y. Charbonnel, J. Dixmier, Sur la représentation coadjointe des algbres de Lie résolubles, J. Reine Angew. Math. 324 (1981), 154–164.
J.-Y. Charbonnel, Sur les orbites de la représentation coadjointe, Compositio Math. 46 (1982), 273–305.
Yu. A. Drozd, Matrix problems, small reduction and representations of a class of mixed Lie groups, in: Representations of Algebras and Related Topics (Kyoto, 1990), London Math. Soc. Lecture Note Ser., Vol. 168, Cambridge Univ. Press, Cambridge, 1992, pp. 225–249.
M. Duflo, Théorie de Mackey pour les groupes de Lie algébriques, Acta. Math. 149 (1982), 153–213.
A. Dvorsky, Generic representations of parabolic subgroups. Case I. \( SO\left( {2n,\mathbb{C}} \right) \), Comm. Algebra 23 (1995), no. 4, 1369–1402.
A. Dvorsky, Generic representations of parabolic subgroups. Case II. \( SO\left( {2n + 1,\,\mathbb{C}} \right) \), Comm. Algebra 24 (1996), no. 1, 259–288.
A. Dvorsky, Index of parabolic and seaweed subalgebras of \( \mathfrak{s}{\mathfrak{o}_n} \), Linear Algebra Appl. 374 (2003), 127–142.
А. Г. Элашвили, Фробениусовы алгебры Ли, Функд. анализ и его прилож. 16 (1982), no. 4, 94–95. Engl. transl.: A. G. Élashvili, Frobenius Lie algebras, Funct. Anal. Appl. 16 (1983), 326–328.
A. G. Elashvili, A. I. Ooms, On commutative polarizations, J. Algebra 26 (2003), no. 1, 129–154.
A. Joseph, A preparation theorem for the prime spectrum of a semisimple Lie algebra, J. Algebra 48 (1977), no. 2, 241–289.
Y. Khakimdjanov, M. Goze, A. Medina, Symplectic or contact structures on Lie groups, Differential Geom. Appl. 21 (2004), no. 1, 41–54.
T. Kimura, Introduction to Prehomogeneous Vector Spaces, Translations of Mathematical Monographs, Vol. 215, American Mathematical Society, Providence, RI, 2003.
А. А. Кириллов, Унитарные представления нильпотентных групп Ли, УМН 17 (1962), no. 4(106), 57–110. Engl. transl.: A. A. Kirillov, Unitary representations of nilpotent Lie groups, Russ. Math. Surv. 17 (1962), no. 4, 53–104.
B. Kostant, The cascade of orthogonal roots and the coadjoint structure of the nilradical of a Borel subgroup of a semisimple Lie group, à paraître dans Moscow Math. J., arXiv:1101.5382.
Y. Kosmann. S. Sternberg, Conjugaison des sous-algèbres d’isotropie, C. R. Acad. Sci. Paris Sér. A 279 (1974), 777–779.
M. S. Khalgui, P. Torasso, Formule de Poisson–Plancherel pour un groupe presque algébrique réel, I. Transformée de Fourier d’intégrales orbitales, J. Funct. Anal. 116 (1993), 359–440.
M. S. Khalgui, P. Torasso, La formule de Plancherel pour les groupes de Lie presque algébriques réels, J. Funct. Anal. 235 (2006), 449–542.
A. Moreau, O. Yakimova, Coadjoint orbits of reductive type of seaweed Lie algebras, à paraître dans Int. Math. Res. Not., arXiv:1101.0902.
A. I. Ooms, On Frobenius Lie algebras, Comm. Algebra 8 (1980), no. 1, 13–52.
D. I. Panyushev, An extension of Raïs’ theorem and seaweed subalgebras of simple Lie algebras, Ann. Inst. Fourier (Grenoble) 55 (2005), no. 3, 693–715.
A. Premet, S. Skryabin, Representations of restricted Lie algebras and families of associative
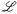 -algebras, J. Reine Angew. Math. 507 (1999), 189–218.
-algebras, J. Reine Angew. Math. 507 (1999), 189–218.P. Tauvel, R. W. T. Yu, Indice et formes linéaires stables dans les algbres de Lie, J. Algebra 273 (2004), 507–516.
P. Tauvel, R. W. T. Yu, Sur l’indice de certaines algbres de Lie, Ann. Inst. Fourier 54 (2004), no. 6, 1793–1810.
P. Tauvel, R. W. T. Yu, Lie Algebras and Algebraic Groups, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2005.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Duflo, M., Khalgui, M.S. & Torasso, P. Algèbres de Lie quasi-réductives. Transformation Groups 17, 417–470 (2012). https://doi.org/10.1007/s00031-012-9179-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00031-012-9179-4



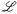 -algebras, J. Reine Angew. Math. 507 (1999), 189–218.
-algebras, J. Reine Angew. Math. 507 (1999), 189–218.