Long-time behavior of solutions to the generalized Allen–Cahn model with degenerate diffusivity

Abstract

The generalized Allen–Cahn equation,

$$\begin{aligned} u_t=\varepsilon ^2(D(u)u_x)_x-\frac{\varepsilon ^2}{2}D'(u)u_x^2-F'(u), \end{aligned}$$

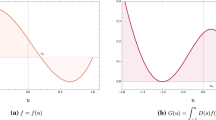
with nonlinear diffusion, $D = D(u)$, and potential, $F = F(u)$, of the form

$$\begin{aligned} D(u) = |1-u^2|^{m}, \quad \text {or} \quad D(u) = |1-u|^{m}, \quad m >1, \end{aligned}$$

and

$$\begin{aligned} F(u)=\frac{1}{2n}|1-u^2|^{n}, \qquad n\ge 2, \end{aligned}$$

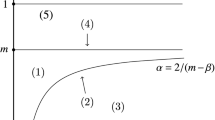
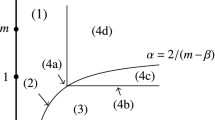
respectively, is studied. These choices correspond to a reaction function that can be derived from a double well potential, and to a generalized degenerate diffusivity coefficient depending on the density u that vanishes at one or at the two wells, $u = \pm 1$. It is shown that interface layer solutions that are equal to $\pm 1$ except at a finite number of thin transitions of width $\varepsilon$ persist for an either exponentially or algebraically long time, depending upon the interplay between the exponents n and m. For that purpose, energy bounds for a renormalized effective energy potential of Ginzburg–Landau type are derived.