Hypersimplicial subdivisions

Abstract

Let $\pi :{\mathbb {R}}^n \rightarrow {\mathbb {R}}^d$ be any linear projection, let A be the image of the standard basis. Motivated by Postnikov’s study of postitive Grassmannians via plabic graphs and Galashin’s connection of plabic graphs to slices of zonotopal tilings of 3-dimensional cyclic zonotopes, we study the poset of subdivisions induced by the restriction of $\pi$ to the k-th hypersimplex, for $k=1,\dots ,n-1$. We show that: For arbitrary A and for $k\le d+1$, the corresponding fiber polytope ${\mathcal {F}}^{(k)}(A)$ is normally isomorphic to the Minkowski sum of the secondary polytopes of all subsets of A of size $\max \{d+2,n-k+1\}$. When $A=\mathbf {P}_{n}$ is the vertex set of an n-gon, we answer the Baues question in the positive: the inclusion of the poset of $\pi$-coherent subdivisions into the poset of all $\pi$-induced subdivisions is a homotopy equivalence. When $A=\mathbf {C}(d,n)$ is the vertex set of a cyclic d-polytope with d odd and any $n \ge d+3$, there are non-lifting (and even more so, non-separated) $\pi$-induced subdivisions for $k=2$.

1 Introduction

The main object of study in this paper are hypersimplicial subdivisions, defined as follows. Let A be a set of n points affinely spanning ${\mathbb {R}}^d$. Let $\Delta _n$ be the standard $(n-1)$-dimensional simplex in ${\mathbb {R}}^n$. Consider the linear projection $\pi : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^d$ sending the vertices of $\Delta ^n$ to the points in A. (We implicitly consider the points in A labelled by [n], so that $\pi$ sends $e_i$ to the point labelled by i). Let $\Delta _n^{(k)} {:}{=} k\Delta _n \cap [0,1]^n$ be the standard hypersimplex and $A^{(k)}$ the image of the vertices of $\Delta _n^{(k)}$ under $\pi$ (so that points in $A^{(k)}$ are labelled by k-subsets of [n]). A hypersimplicial subdivision of $A^{(k)}$ is a polyhedral subdivision of ${{\,\mathrm{conv}\,}}(A^{(k)})$ such that every face of the subdivision is the image of a face of $\Delta _n^{(k)}$ under $\pi$. Put differently, we call hypersimplicial subdivisions the $\pi$-induced subdivisions of the projection $\pi : \Delta _n^{(k)} \rightarrow {{\,\mathrm{conv}\,}}(A^{(k)})$, as introduced in [3, 5] (see also [8, 18]). See more details in Sect. 2.

One reason to study such subdivisions comes from the case where $A\subset {\mathbb {R}}^2$ are the vertices of a convex polygon. Galashin [10] shows that in this case fine hypersimplicial subdivisions, which we call hypertriangulations, are in bijection with maximal collections of chord-separated k-sets. These, in turn, correspond to reduced plabic graphs, [15] which are a fundamental tool in the study of the positive Grassmannian [16, 17].

More generally, it is of interest the case where A are the vertices of a cyclic polytope $\mathbf {C}(n,d) \subset {\mathbb {R}}^d$. (The n-gon is the case $d=2$). In [17, Problem 10.3] Postnikov asks the generalized Baues problem for this scenario; that is, he asks whether the poset of hypersimplicial subdivisions of $\mathbf {C}(n,d)^{(k)}$ has the homotopy type of a $(n-d-2)$-sphere. For $k=1$ this was shown to have a positive answer by Rambau and Santos [19]. For $d=2$, Balitskiy and Wellman show the poset to be simply connected and again ask the Baues question for it ( [6, Theorem 6.4 and Question 6.1]). We here give the answer to this:

Theorem 1.1

(Theorem 6.17) Let $\mathbf {P}_{n}$ be the vertices of any convex n-gon. The poset of hypersimplicial subdivisions ${\mathcal {B}}(\Delta _n^{(k)} \rightarrow \mathbf {P}_{n}^{(k)})$ deformation retracts onto the poset of coherent hypersimplicial subdivisions. In particular, it has the homotopy type of an $(n-4)$-sphere.

Postnikov [17, Problem 10.3] also asks for which values of the parameters can all hypersimplicial subdivisions of $\mathbf {C}(n,d)^{(k)}$ be lifted to zonotopal tilings of the cyclic zonotope. This was already known to be false for $d=1$ [17, Example 10.4] and we generalize the counterexamples to every odd dimension:

Theorem 1.2

(Corollary 5.4) Consider the cyclic polytope $\mathbf {C}(n,d)\subset {\mathbb {R}}^d$ for odd d and $n\ge d+3$. Then, for every $k\in [2,n-2]$ there exist hypersimplicial subdivisions of $\mathbf {C}(n,d)^{(k)}$ that do not extend to zonotopal tilings of the cyclic zonotope $Z(\mathbf {C}(n,d))$.

Galashin [10] showed that the answer to Postnikov’s question is positive for hypertriangulations of $\mathbf {P}_{n}$, a result that was generalized to all hypersimplicial subdivisions of $\mathbf {P}_{n}$ by Balitskiy and Wellman [6, Lemma 6.3]. In Example 5.1 we show that the same does not hold for other two-dimensional configurations.

The poset of coherent hypersimplicial subdivisions of any A is isomorphic to the face poset of a polytope, a particular case of a fiber polytope. When $k=1$ this is just the secondary polytope of A, so for $k>1$ we call it the k-th hypersecondary polytope of A. A related, but different, polytope is studied in [12] (see Remark 2.7).

We study hypersecondary polytopes for any $A\subset {\mathbb {R}}^d$ and $k\le d+1$. Specifically, we show that these polytopes are normally equivalent to the Minkowski sum of certain faces of the secondary polytope of A. By symmetry, an analogue statement holds for $n-d-1\le k<n$.

Theorem 1.3

(Theorem 3.11) Let $A\subseteq {\mathbb {R}}^d$ be a configuration of size n and $k\in [d+1]$. Let $s = \max (n-k+1, d+2)$. The hypersecondary polytope ${\mathcal {F}}^{(k)}(A)$ is normally equivalent to the Minkowski sum of the secondary polytopes of all subsets of A of size s.

The paper is organized as follows: Sect. 2 introduces notation and basic background on induced subdivisions in general, and hypersimplicial subdivisions in particular. In Sect. 3 we look at coherent hypersimplicial subdivisions and hypersecondary polytopes as Minkowski sums and prove Theorem 1.3, among other results. In Sect. 4 we study the connection of hypersimplicial subdivisions with zonotopal tilings. In particular, we extend to tiles of positive dimension the concept of A-separated sets introduced in [11]. With this machinery we show that if all hypertriangulations of A are separated then all hypersubdivisions are separated too (Corollary 4.12). In Sects. 5 and 6 we prove Theorem 1.2 and Theorem 1.1 respectively. We also briefly discuss the enumeration of hypersimplicial subdivisions of $\mathbf {P}_{n}^{(2)}$ in Sect. 6.2.

2 Preliminaries and notation

2.1 Fiber polytopes

We here briefly recall the main concepts and results on fiber polytopes. See [5] or [18] for more details.

Let $\pi : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^d$ be a linear projection map. Let $Q\subset {\mathbb {R}}^n$ be a polytope and let $A=\pi ({{\,\mathrm{vertices}\,}}(Q)$). A $\pi$-induced subdivision of A is a polyhedral subdivision S (in the sense of, for example, [8]), such that every face of S is the image under $\pi$ of a face F of Q.

Given a vector $w\in ({\mathbb {R}}^n)^*$ the face $Q^w$ of Q selected by w is the convex hull of all vertices of Q which minimize w. A $\pi$-coherent subdivison is a $\pi$-induced subdivision in which the faces of Q are chosen “coherently” via a vector $w\in ({\mathbb {R}}^n)^*$. More precisely, we define the $\pi$-coherent subdivision of A given by w to be

$$\begin{aligned} S(Q {\mathop {\rightarrow }\limits ^{\pi }} A,w) {:}{=} \left\{ \pi (F) : \exists {\tilde{w}}\in ({\mathbb {R}}^n)^* \ s.t.\ {\tilde{w}}|_{\ker (\pi )} = w|_{\ker (\pi )} ,\ Q^{{\tilde{w}}} = F\right\} . \end{aligned}$$

The fiber fan of the projection $Q {\mathop {\rightarrow }\limits ^{\pi }} A$ is the stratification of $({\mathbb {R}}^n)^*$ according to what $\pi$-coherent subdivision is produced. It is a polyhedral fan with lineality space equal to

$$\begin{aligned} \{w \in ({\mathbb {R}}^n)^* : \ker (\pi ) \subset \ker (w)\} + \{w \in ({\mathbb {R}}^n)^* : w|_Q=\text {constant}\}. \end{aligned}$$

As we will see below, it is the normal fan of a certain polytope ${\mathcal {F}}(Q {\mathop {\rightarrow }\limits ^{\pi }} A)$ of dimension $\dim (Q) - \dim (A)$.

To define ${\mathcal {F}}(Q {\mathop {\rightarrow }\limits ^{\pi }} A)$, we look at fine $\pi$-induced subdivisions. A $\pi$-induced subdivision S is fine if $\dim (F)=\dim (\pi (F))$ for each of the faces $F\le Q$ whose images are cells in S. Put differently, a fine $\pi$-induced subdivision is the image of a subcomplex of Q that is a section of $\pi :Q\rightarrow {{\,\mathrm{conv}\,}}(A)$. To each fine $\pi$-induced subdivision S we associate the following point:

$$\begin{aligned} {{\,\mathrm{GKZ}\,}}(S){:}{=} \sum _{\begin{array}{c} F\le Q \\ \pi (F)\in S \end{array}} \frac{{{\,\mathrm{vol}\,}}(\pi (F))}{{{\,\mathrm{vol}\,}}(A)} \mathbf{c}(F) \in {\mathbb {R}}^n, \end{aligned}$$

where $\mathbf{c}(F)$ denotes the centroid of F.

Definition 2.1

The fiber polytope of the projection $\pi : Q \rightarrow {{\,\mathrm{conv}\,}}(A)$ is the convex hull of the vectors ${{\,\mathrm{GKZ}\,}}(S)$ for all fine $\pi$-induced subdivisions. We denote it ${\mathcal {F}}(Q\rightarrow A)$.

The main property of the fiber polytope is the following result of Billera and Sturmfels. In fact, for the purposes of this paper this theorem can be taken as a definition of the fiber polytope, since our results are mostly not about the polytope but about its normal fan (see, eg Sect. 3).

Theorem 2.2

(Billera and Sturmfels [5]) ${\mathcal {F}}(Q\rightarrow A)$ is a polytope of dimension $\dim (Q) - \dim (A)$ whose normal fan equals the fiber fan.

In particular, the face lattice of ${\mathcal {F}}(Q\rightarrow A)$ is isomorphic to the poset of $\pi$-coherent subdivisions ordered by refinement. For example, vertices of ${\mathcal {F}}(Q\rightarrow A)$ correspond bijectively to fine $\pi$-coherent subdivisions.

The following two cases of this construction are of particular importance. Let $A=\{a_1,\dots ,a_n\}\subset {\mathbb {R}}^d$ be a configuration of n points. Then:

• (1) If we let $\pi : \Delta _n \rightarrow {{\,\mathrm{conv}\,}}(A)$ be the affine map $e_i\mapsto a_i$ bijecting vertices of $\Delta _n$ to A, then all the polyhedral subdivisions of A are $\pi$-induced, and the coherent ones are usually called regular subdivisions of A. The corresponding fiber polytope is the secondary polytope of A and we denote it ${\mathcal {F}}^{(1)}(A)$ (in the next sections we define ${\mathcal {F}}^{(k)}(A)$ for other values of k).

• (2) Let

  $$\begin{aligned} Z(A) = \sum _{i} {{\,\mathrm{conv}\,}}\left( 0,(a_i,1) \right) \subset {\mathbb {R}}^{d+1} \end{aligned}$$

  be the zonotope generated by the vector configuration $A\times \{1\}\subset {\mathbb {R}}^{d+1}$. The $\pi$ in the previous case extends to a linear map $\pi : [0,1]^n \rightarrow Z(A)$ still sending $e_i\mapsto a_i$. Then the $\pi$-induced subdivisions are precisely the zonotopal tilings of Z(A). The corresponding fiber polytope is the fiber zonotope of Z(A) (or of A) and we denote it ${\mathcal {F}}^Z(A)$.

2.2 The Baues problem

The poset of all $\pi$-induced subdivisions (excluding the trivial subdivision for technical reasons) is called the Baues poset of the projection and we denote it ${\mathcal {B}}(Q\rightarrow A)$. The subposet of $\pi$-coherent subdivisions is denoted ${\mathcal {B}}_{{{\,\mathrm{coh}\,}}}(Q\rightarrow A)$. The Baues problem is, loosely speaking, the question of how similar are ${\mathcal {B}}(Q\rightarrow A)$ and ${\mathcal {B}}_{{{\,\mathrm{coh}\,}}}(Q\rightarrow A)$, formalized as follows:

To every poset ${\mathcal {P}}$ one can associate a simplicial complex called the order complex of ${\mathcal {P}}$ by using the elements of ${\mathcal {P}}$ as elements and chains in the poset as simplices. In particular, one can speak of the homotopy type of ${\mathcal {P}}$ meaning that of its order complex. Similarly, an order preserving map of posets

$$\begin{aligned} f: {\mathcal {P}}_1 \rightarrow {\mathcal {P}}_2 \end{aligned}$$

induces a simplicial map between the corresponding order complexes, and one can speak of the homotopy type of f.

The prototypical example is the following: if ${\mathcal {P}}$ is the face poset of a polyhedral complex ${\mathcal {C}}$, then the order complex of ${\mathcal {P}}$ is (isomorphic to) the barycentric subdivision of ${\mathcal {C}}$. In particular, since ${\mathcal {B}}_{{{\,\mathrm{coh}\,}}}(Q\rightarrow A)$ is the face poset of the polytope ${\mathcal {F}}(Q\rightarrow A)$, it is homotopy equivalent (in fact, homeomorphic) to a sphere of dimension $\dim (Q) - \dim (A) -1$.

Question 2.3

(Baues Problem) Under what conditions is the inclusion ${\mathcal {B}}_{{{\,\mathrm{coh}\,}}}(Q\rightarrow A) \hookrightarrow {\mathcal {B}}(Q\rightarrow A)$ a homotopy equivalence?

See [18] for a (not so recent) survey about this question, and [13, 22] for examples where the answer is no and having Q a simplex and a cube, respectively. See Theorem 2.5 for examples, onvolving cyclic polytopes, where the answer to the Baues Problen is known to be positive. Another important case for us is when A is 2-dimensional. The following is known:

Theorem 2.4

Consider the Baues problem for a projection with $\dim (A)=2$.

• (1) If Q is a simplex then ${\mathcal {B}}_{{{\,\mathrm{coh}\,}}}(Q\rightarrow A) \hookrightarrow {\mathcal {B}}(Q\rightarrow A)$ is a homotopy equivalence [9].

• (2) There is a 5-polytope Q with ten vertices and a projection $Q\rightarrow {\mathbb {R}}^2$ for which ${\mathcal {B}}(Q\rightarrow A)$ is not homotopy equivalent to a sphere (hence not homotopy equivalent to ${\mathcal {B}}_{{{\,\mathrm{coh}\,}}}(Q\rightarrow A)$) [20].

2.3 Cyclic polytopes

Cyclic polytopes are a family of polytopes of particular interest for this manuscript and are defined as follows. The trigonometric moment curve (also known as the Carathéodory curve), is parametrized by

$$\begin{aligned} \phi _d: t \rightarrow (\sin (t),\cos (t),\sin (2t),\cos (2t),\dots )\in {\mathbb {R}}^d. \end{aligned}$$

Let $t_1,\dots ,t_n$ be n cyclically equidistant numbers in $[0,2\pi )$, for example, $t_i = \frac{2\pi (i-1)}{n}$. The cyclic polytope $\mathbf {C}(n,d)$ is the convex hull of $\phi (t_1),\dots ,\phi (t_n)$.

The combinatorics of the cyclic polytope can be nicely described in terms of the circuits of the corresponding oriented matroid. Namely, all circuits are of the form $(\{a_1,a_3,\dots \}, \{a_2,a_4,\dots \})$ such that $a_1<a_2<\dots <a_{d+2}$ and their opposites (giving the label i to the vertex $\phi (t_i)$).

Cyclic polytopes are more commonly defined using the polynomial moment curve $t\rightarrow (t,t^2,\dots ,t^d)$ instead of the trigonometric moment curve. Their combinatorial type (that is, their face lattice) is the same for both models, and for all choices of the parameters $t_1,\dots ,t_n$. However, the coherence of subdivisions, and hence the combinatorial type of the corresponding fiber polytopes, depends on the embedding, as we mention in Example 3.12. Using the trigonometric moment curve with equally spaced parameters has the advantage that it makes even dimensional cyclic polytopes have additional symmetry, namely the cyclic group action on the vertices. (For points in the polynomial curve or non-equally spaced parameters in the trigonometric curve, this cyclic symmetry is only combinatorial). When $d=2$ the cyclic polytope $\mathbf {C}(n,2)$ is a regular polygon and we abbreviate it by $\mathbf {P}_{n}$.

The Baues problem is known to have positive answer for cyclic polytopes in the following two cases:

Theorem 2.5

([19, 23]) Let $n >d \in {\mathbb {N}}$. Then, the following two cases of the Baues question have a positive answer:

• When $Q=\Delta _n$ and $A=\mathbf {C}(n,d)$ is the cyclic polytope of dimension d with n vertices [19].

• When $Q=[0,1]^n$ and $A=Z(\mathbf {C}(n,d))$ is the cyclic zonotope of dimension $d+1$ with n generators [23].

2.4 Hypersecondary polytopes

Let $A=\{a_1,\dots , a_n\}\in {\mathbb {R}}^d$ be a point configuration. For each $k=1,\dots ,n-1$ we consider the following k-th deleted (Minkowski) sum of A with itself, which we denote $A^{(k)}$:

$$\begin{aligned} A^{(k)} {:}{=} \left\{ a_{i_1} + \dots + a_{i_k} \in {\mathbb {R}}^d : \{i_1,\dots , i_k\} \in \left( {\begin{array}{c}[n]\\ k\end{array}}\right) \right\} . \end{aligned}$$

The k-th deleted sum of the standard $(n-1)$-simplex $\Delta _{n} {:}{=}{{\,\mathrm{conv}\,}}(e_1,\dots ,e_n)$ equals the k-th hypersimplex of dimension $n-1$:

$$\begin{aligned} \Delta _n^{(k)} {:}{=} {{\,\mathrm{conv}\,}}\left( \left\{ \sum _ {i\in B} e_i : B\in \left( {\begin{array}{c}[n]\\ k\end{array}}\right) \right\} \right) = [0,1]^n \cap \left\{ x:\sum _{i=1}^n x_i = k\right\} . \end{aligned}$$

(Observe that the notation $\Delta _n^{(k)}$ is an abbreviation of ${{\,\mathrm{conv}\,}}({{\,\mathrm{vertices}\,}}(\Delta _n)^{(k)}))$.

As mentioned above, the projection ${\mathbb {R}}^n\rightarrow {\mathbb {R}}^d \times \{1\}$ that sends the vertices of $\Delta _n$ to A extends to a linear map ${\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{d+1}$ that sends the unit cube $[0,1]^n$ to the zonotope Z(A). In turn, this linear map restricts to an affine map sending each $\Delta _n^{(k)}\subset {\mathbb {R}}^n$ to $A^{(k)}\subset {\mathbb {R}}^d \times \{k\}$. We use the same letter $\pi$ for all these projections.

Definition 2.6

The $\pi$-induced subdivisions of the projection $\pi : \Delta _n^{(k)} \rightarrow A^{(k)}$ are called hypersimplicial subdivisions of level k of A, or just hypersimplicial subdivisions of $A^{(k)}$. Fine hypersimplicial subdivisions are called hypertriangulations. We denote ${\mathcal {B}}^{(k)}(A)$ and ${\mathcal {F}}^{(k)}(A)$ the corresponding Baues poset and fiber polytope, and call the latter the k-th hypersecondary polytope of A. We denote ${\mathcal {B}}_{{{\,\mathrm{coh}\,}}}^{(k)}(A)$ for the coherent subdivisions in ${\mathcal {B}}^{(k)}(A)$.

Remark 2.7

In parallel to our work, Galashin, Postnikov and Williams have studied a similar polytope which they call higher secondary polytope [12]. We want to emphasize that these are not the same as the hypersecondary polytopes of Definition 2.6. However, they are related. In particular, hypersecondary polytopes can be constructed as Minkowski sums of higher secondary polytopes (see [12, Theorem 2.2]). We provide a different decomposition of the hypersecondary polytope into Minkowski summands in Theorem 3.11. Higher secondary polytopes as well as hypersecondary polytopes are further studied in [2] for the case $d=1$ (in our notation).

2.5 Lifting subdivisions

By construction, the intersection of any zonotopal tiling of Z(A) with the hyperplane $\sum x_i = k$ is a hypersimplicial subdivision of $A^{(k)}$. But the converse is in general not true. Not every hypersimplicial subdivision of $A^{(k)}$ “extends” to a zonotopal tiling of Z(A). Following [17] the ones that extend are called lifting hypersimplicial subdivisions. (In the case $k=1$ the name “lifting” for these subdivisionss established in [4], and used because, via the Bohne-Dress Theorem, they are exactly the ones that can be “lifted” in the oriented matroid sense. See also [21].) The following are examples of them:

• Any $\pi$-coherent subdivision of $A^{(k)}$ is lifting. Indeed, the subdivision of $A^{(k)}$ given by the vector $w\in ({\mathbb {R}}^*)$ is equal to the restriction to $A^{(k)}$ of the subdivsion of Z(A) given by w. However, the converse is not true (see Example 2.9).

• For a cyclic polytope $\mathbf {C}(n,d)$, all triangulations in the standard sense (that is, all hypertriangulations of $\mathbf {C}(n,d)^{(1)}$) are lifting [19]. The same is not known for non-simplicial subdivisions.

• For arbitrary k and a convex n-gon $\mathbf {P}_{n}$, all hypertriangulations of $\mathbf {P}_{n}^{(k)}$ are lifting [10]. The same result for all hypersimplicial subdivisions has recently been proved in [6].

The fact that all hypertriangulations of $\mathbf {P}_{n}^{(k)}$ are lifting does not inmediatly imply a positive answer to the Baues problem for this case, as there are non-coherent lifting triangulations (see Example 2.9). So the posets ${\mathcal {B}}^{(k)}(\mathbf {P}_{n})$ and ${\mathcal {B}}^{(k)}(\mathbf {P}_{n})$ do not coincide in general. Non-lifting triangulations of $A^{(1)}$ are not known in dimension two but easy to construct in dimension three or higher. For example, if a subdivision S of A has the property that its restriction to some subset B of A cannot be extended to a subdivision of B, then S is non-lifting. Such subdivisions (and triangulations) exist when A is the vertex set of a triangular prism together with any point in the interior of it, the vertex set of a 4-cube, or the vertex set of $\Delta _4\times \Delta _4$, among other cases (see, e.g., [21, Chapter 5], or [8, Proof (10) in Sect. 7.1.2]).

To better understand lifting subdivisions, let us look at zonotopal tilings of Z(A). We denote ${\mathcal {B}}^Z (A)$, ${\mathcal {B}}_{{{\,\mathrm{coh}\,}}}^Z (A)$ and ${\mathcal {F}}^Z (A)$ for the poset of zonotopal tilings, its subposet of coherent tilings and the secondary zonotope of Z(A) respectively. We call any subset of [n] a point, since it represents an element of the point configuration $\sum _{i\in [n]} \{0, a_i\}$. A tile is a poset interval [X, Y] of the boolean poset $2^{[n]}$, where $X\subseteq Y$. To be precise, $[X,Y] {:}{=} \{I \subseteq [n] : X\subseteq I \subseteq Y\}$. Geometrically, we think of [X, Y] as the zonotope $X + Z(Y\setminus X)$, but we prefer the combinatorial notation where the tile is described as the set of vertices of $[0,1]^n$ of which it is the projection.

Every tile [X, Y] is a cell in a coherent zonotopal tiling of Z(A), specifically in the one given by the vector $w\in ({\mathbb {R}}^*)^n$ where

$$\begin{aligned} w(e_j) = {\left\{ \begin{array}{ll} -1, &{} \text {for } j\in X\\ 0, &{} \text {for } j\in Y\backslash X\\ 1, &{} \text {for } j\in [n]\backslash Y. \end{array}\right. } \end{aligned}$$

Indeed, this w gives value at least $-|X|$ to every point in Z(A), with equality if and only if the point belongs to [X, Y].

Every face of the hypersimplex $\Delta _n^{(k)}$ is the intersection of a face of $[0,1]^n$ with the hyperplane $\left\{ x:\sum _{i=1}^n x_i = k\right\}$. Therefore we can denote the projection under $\pi$ of any face of $\Delta _n^{(k)}$ by

$$\begin{aligned}{}[X,Y]^{(k)} {:}{=} [X,Y]\cap \left( {\mathbb {R}}^d\times \{k\}\right) = \{B : X\subseteq B \subseteq Y \quad |B| = k\}. \end{aligned}$$

Similarly, for a collection S of tiles we denote

$$\begin{aligned} S^{(k)} : = \{ [X,Y]^{(k)} : [X,Y] \in S\}. \end{aligned}$$

By definition, a subdivision of $A^{(k)}$ is hypersimiplicial if and only if all of its cells are of the form $[X,Y]^{(k)}$. A hypersimplicial subdivision is fine if for every cell $[X,Y]^k$ we have that $Y\backslash X$ is an affine basis in A. We say that a tile [X, Y] covers level k, if $|X|<k<|Y|$. In other words, [X, Y] covers level k if $[X,Y]^{(k)}$ is of positive dimension.

This spells out the following relation with zonotopal tilings:

Proposition 2.8

For every configuration A of n points and every $k\in [n-1]$:

• (1) Intersection of zonotopal tilings with the hyperplane at level k induces an order-preserving map

  $$\begin{aligned} r^{(k)}: {\mathcal {B}}^Z(A) \rightarrow&{\mathcal {B}}^{(k)}(A) .\\ S \quad \mapsto&\quad S^{(k)} \end{aligned}$$

• (2) The normal fan of ${\mathcal {F}}^Z(A)$ refines the normal fan of ${\mathcal {F}}^{(k)}(A)$.

Proof

For the first claim, notice that $S^{(k)}$ equals the intersection of the zonotopal tiling S with the hyperplane ${\mathbb {R}}^d\times \{k\}$ containing $A^{(k)}$, which clearly is hypersimplicial. The second claim follows from the fact that $S(Z(A),w)^{(k)} = S(A^{(k)}, w)$ for every $w\in ({\mathbb {R}}^n)^*$. $\square$

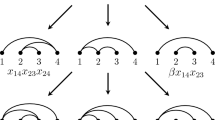
Example 2.9

Consider the regular hexagon $\mathbf {P}_{6}$. Figure 1 shows a hypersimplicial subdivision of $\mathbf {P}_{6}^{(2)}$ whose set of facets are the triangles $[\emptyset ,123]^{(2)}$, $[\emptyset ,135]^{(2)}$, $[\emptyset ,156]^{(2)}$, $[\emptyset ,345]^{(2)}$, $[1,1236]^{(2)}$, $[1,1356]^{(2)}$, $[3,1235]^{(2)}$, $[3,2345]^{(2)}$, $[5,1345]^{(2)}$ and $[5,1456]^{(2)}$. The colour of the triangle $[X,Y]^{(2)}$ is dark gray if $X =\emptyset$ and white if $|X|=1$, which agrees with the colouring of vertices of the corresponding plabic graph (see [10]).

This subdivision is not coherent. To see this, suppose there is a lifting vector $w\in ({\mathbb {R}}^*)^6$ whose regular subdivision is this. Then notice that the presence of the edge $[1,136]^{(2)}$ implies $w_3+w_6<w_2+w_5$, the presence of the edge $[3,235]^{(2)}$ implies $w_2+w_5<w_1+w_4$ and the presence of the edge $[5,145]^{(2)}$ implies $w_1+w_4<w_3+w_6$, together forming a contradiction. This contrasts the fact that every subdivision of a convex polygon is regular. This example is an adaptation of a classical construction from which many non-coherent subdivisions are derived [8, Example 5.1.4].

Fig. 1

A non-coherent hypersimplicial subdivision of $\mathbf {P}_{6}^{(2)}$

2.6 Lifting subdivisions via Gale transforms. The Bohne-Dress Theorem

As a general reference for the contents of this section we recommend the book [8], more specifically Chapters 4, 5 and 9.

A Gale transform of a point configuration $A=\{a_1,\dots ,a_n\}$ is a vector configuration $\mathbf {G}_{A}=\{a^*_1,\dots , a^*_n\}$ with the property that a vector $(\lambda _1,\dots ,\lambda _n)\in {\mathbb {R}}^n$ is the coefficient vector of an affine dependence in A if and only if it is the vector of values of a linear functional on $\mathbf {G}_{A}$. The definition implicitly assumes a bijection between A and $\mathbf {G}_{A}$ given by the labels $1,\dots ,n$.

Gale duality is an involution: the Gale duals of a Gale dual of A are linearly isomorphic to A when considering A as a vector configuration via homogenization, by which we mean looking at affine geometry on the points $a_1,\dots ,a_n$ as linear algebra on the vectors $(a_1,1), \dots , (a_n,1)$. In fact, if A and B are Gale duals to one another then their oriented matroids are dual, which implies that their ranks add up to n. In our setting where A has affine dimension d and hence rank $d+1$, its Gale duals have rank $n-d-1$.

The normal fan of the secondary polytope ${\mathcal {F}}^{(1)}(A)$ of A lives naturally in the ambient space of $\mathbf {G}_{A}$: it equals the common refinement of all the complete fans with rays taken from $\mathbf {G}_{A}$. Put differently, vectors $w \in {{\,\mathrm{span}\,}}(\mathbf {G}_{A})$ are in natural bijection to lifting functions $A\rightarrow {\mathbb {R}}$ (where the latter, which forms a linear space isomorphic to ${\mathbb {R}}^n$, is considered modulo the linear subspace of affine functions restricted to A). Under this identification, $w_1$ and $w_2$ define the same coherent subdivision of A if and only if they lie in exactly the same family of cones among the finitely many cones spanned by subsets of B. The precise combinatorial rule to construct the coherent subdivision $S=S(\Delta _n {\mathop {\rightarrow }\limits ^{\pi }} A,w)$ of A induced by a $w\in {{\,\mathrm{span}\,}}( \mathbf {G}_{A} )$ is: a subset $Y\subset [n]$ is a cell in S if and only if w lies in the relative interior of $[n]\backslash Y$.

This rule can be made purely combinatorial as follows. Instead of starting with a vector $w\in {{\,\mathrm{span}\,}}(\mathbf {G}_{A})$, let ${\mathcal {M}}^*(A)$ be the oriented matroid of $\mathbf {G}_{A}$ and let ${\mathcal {M}}'$ be a single-element extension of ${\mathcal {M}}^*(A)$. That is, ${\mathcal {M}}'$ is an oriented matroid of the same rank as ${\mathcal {M}}$ on the ground set $[n]\cup \{w\}$ and such that ${\mathcal {M}}'$ restricted to [n] equals ${\mathcal {M}}^*(A)$. Any vector $w\in {{\,\mathrm{span}\,}}( \mathbf {G}_{A})$ induces such an extension, but the definition is more general since ${\mathcal {M}}'$ needs not be realizable, or it may be realizable but not extend the given realization $\mathbf {G}_{A}$ of ${\mathcal {M}}^*(A)$. Yet, any such extension w allows to define a subdivision S(w) of A as follows.

Proposition 2.10

With the notation above, the following rules define, respectively, a polyhedral subdivision $S^{(1)}(A,w)$ of A and a zonotopal tiling $S^{(Z)}(A,w)$ of Z(A):

• (1) A subset $Y\subset [n]$ is a cell in $S^{(1)}(A,w)$ if and only if $([n]\setminus Y, \{w\})$ is a vector in the oriented matroid ${\mathcal {M}}'$.

• (2) An interval [X, Y] is a tile in $S^{(Z)}(A,w)$ if and only if $([n]\setminus Y, X \cup \{w\})$ is a vector in the oriented matroid ${\mathcal {M}}'$.

By construction, $S^{(1)}(A,w)$ is the slice at height 1 of $S^{(Z)}(A,w)$. In fact:

Theorem 2.11

(Bohne-Dress Theorem) The construction of Proposition 2.10(2) is a bijection (and a poset isomorphism, with the weak map order on extensions of ${\mathcal {M}}^*(A)$) between one-element extensions of ${\mathcal {M}}^*(A)$ and zonotopal tilings of Z(A). In particular, lifting subdivisions of $A^{(1)}$ are precisely the ones that can be obtained by the construction in Proposition 2.10(1).

3 Normal fans of hypersecondary polytopes

The goal of this section is to study hypersecondary polytopes, and the relations between them and the secondary zonotope. Most of such relations say that the normal fan of one of the polytopes refines that of another one. We introduce the following definition to this effect:

Definition 3.1

Let $P, Q \in {\mathbb {R}}^d$ be two polytopes. We say that Q is a Minkowski summand of P, and write $Q \le P$, if any of the following equivalent conditions holds:

• (1) The normal fan of P refines that of Q.

• (2) $P+Q$ is combinatorially isomorphic to P.

If P and Q are Minkowski summands of one another then they are normally equivalent and we write $P\cong Q$.

Remark 3.2

The equivalence of these two conditions follows from the fact that the normal fan of $P+Q$ is the common refinement of the normal fans of P and Q. It can be shown $Q\le P$ is also equivalent to the existence of a polytope $Q'$ and an $\varepsilon >0$ such that $P=Q'+\varepsilon Q$, hence the name “Minkowski summand”.

Throughout this section we will assume that $A\subseteq {\mathbb {R}}^d$ is a point configuration that spans affinely ${\mathbb {R}}^d$. As a first example, it follows from Proposition 2.8 that:

Proposition 3.3

For every configuration $A\subset {\mathbb {R}}^d$ of size n:

• (1) ${\mathcal {F}}^{(k)}(A) \le {\mathcal {F}}^Z(A)$.

• (2) Let $k_0=0< k_1< \dots < k_p=n$ be a sequence of integers with $k_{i+1}-k_i \le d+1$ for all i. Then,

  $$\begin{aligned} {\mathcal {F}}^Z(A) \cong \sum _{i=0}^p {\mathcal {F}}^{(k_i)}(A). \end{aligned}$$

Proof

• (1) Let $w\in ({\mathbb {R}}^*)^n$. The coherent zonotopal tiling of Z(A) given by w restricts to $A^{(k)}$ to the coherent hypersimplicial subdivision of $A^{(k)}$ given by w. So the cones of the normal fan of ${\mathcal {F}}^Z(A)$ are always completely contained in a cone of the normal fan of ${\mathcal {F}}^{(k)}(A)$, hence ${\mathcal {F}}^{(k)}(A) \le {\mathcal {F}}^Z(A)$.

• (2) Every full dimensional zonotope [X, Y] in a zonotopal tiling S(Z(A), w) satisfies that $|Y\backslash X| \ge d+1$ so there are at least d integers k between $|X|+1$ and $|Y|-1$ where $[X,Y]^{(k)}$ is a facet of the $S(A^{(k)},w)$. So if we know all the facets of $S(A^{(k_i)})$ for $1\le i \le p$, we know all full dimensional zonotopes $[X,Y]\in S(Z(A),w)$, as each of them appears as $[X,Y]^{(k_i)}\in S(A^{(k_i)},w)$ for some i. Then the subdivision S(Z(A), w) is determined by the subdivisions $S(A^{(k_i)},w)$, so ${\mathcal {F}}^Z(A) \le \sum _{i=0}^p {\mathcal {F}}^{(k_i)}(A)$. The other direction follows from the first part of the proposition.

$\square$

In particular:

Corollary 3.4

For every configuration $A\subset {\mathbb {R}}^d$ of size n,

• (1) If $n \le 2d+2$ then

  $$\begin{aligned} {\mathcal {F}}^Z(A) \cong {\mathcal {F}}^{(k)}(A) , \qquad \forall k\in [n-d-1,d+1]. \end{aligned}$$

• (2) If $n\ge 2d+2$ then

  $$\begin{aligned} \sum _{k=d+1}^{n-d-1} {\mathcal {F}}^{(k)}(A) \cong {\mathcal {F}}^Z(A). \end{aligned}$$

Proof

Just apply Proposition 3.3 to the sequence 0, k, n for case (1), and $0,d+1, d+2,\dots , n-d-1,n$ for case (2). $\square$

Lemma 3.5

Let S be coherent zonotopal subdivision of A and let $B\subseteq A$ be a spanning subset. Then there is at most one $X\subseteq A\backslash B$, such that $[X,X\cup B] \in S$.

Proof

Let $w\in ({\mathbb {R}}^*)^n$ such that $S = S(Z(A),w)$. Since B is of maximal dimension, there is at most one ${\tilde{w}}$ such that $\tilde{w}|_{\ker (\pi )} = w|_{\ker (\pi )}$ and $w\cdot b = 0$ for every $b\in B$. If such ${\tilde{w}}$ exists then the only tile of the form $[X, X\cup B]$ that is in S is the one where $X = \{x\in A : \tilde{w}\cdot x < 0\}$. If no such ${\tilde{w}}$ exists then there is no tile of that form in the subdivision. $\square$

In the following result and in the rest of this section we denote by $A_J$ the subset of A labelled by J, for any $J\subset [n]$.

Lemma 3.6

Fix $k\ge 1$ and a lifting vector $w\in ({\mathbb {R}}^n)^*$, for a point configuration A of size n. For each tile $[X,Y] \subset 2^{[n]}$ such that $Y\backslash X$ a basis of A, the following are equivalent:

• (1) $[X,Y]^{(k+1)}$ is a cell in $S^{(k+1)}(A,w)$.

• (2) There is an $x \in X$ such that $[X\backslash x, Y\backslash x]^{(k)}$ is a cell in $S^{(k)}(A_{[n]\backslash x},w)$ but not in $S^{(k)}(A,w)$.

• (3) For every $x \in X$, $[X\backslash x, Y\backslash x]^{(k)}$ is a cell in $S^{(k)}(A_{[n]\backslash x},w)$ but not in $S^{(k)}(A,w)$.

If, moreover, $k>1$, then they are also equivalent to:

• (4) There are $x_1,x_2\in X$ such that $[X\backslash x_i, Y\backslash x_i]^{(k)}$ is a cell in $S^{(k)}(A_{[n]\backslash x_i},w)$ for $i=1,2$.

• (5) For every $x \in X$, $[X\backslash x, Y\backslash x]^{(k)}$ is a cell in $S^{(k)}(A_{[n]\backslash x},w)$.

Proof

The implication (3)$\Rightarrow$(2) is obvious.

To show (2)$\Rightarrow$(1), consider an x such that the cell $[X\backslash x, Y\backslash x]^{(k)}$ is a cell in $S((A_{[n]\backslash x})^{(k)},w)$. Then by Proposition 2.8, $[X\backslash x, Y\backslash x]$ is a cell of $S(Z(A_{[n]\backslash x}),w)$. Therefore either $[X\backslash x, Y\backslash x]\in S(Z(A),w)$ or $[X,Y]\in S(Z(A),w)$ but not both by Lemma 3.5. In other words, either $[X\backslash x, Y\backslash x]^{(k)}\in S(A^{(k)},w)$ or $[X,Y]^{(k+1)}\in S(A^{(k+1)},w)$ but not both. Since we assumed $[X\backslash x, Y\backslash x]^{(k)}\not \in S(A^{(k)},w)$, we are done.

To see (1)$\Rightarrow$(3), notice that if $[X,Y]^{(k+1)}\in S(A^{(k+1)},w)$ then $[X,Y]\in S(Z(A),w)$. So, for all $x \in X$ we have that the tile $[X\backslash x, Y\backslash x]$ is a cell of $S(Z(A_{[n]\backslash x}),w)$. In particular, $[X\backslash x, Y\backslash x]^{(k)}\in S((A_{[n]\backslash h})^{(k)},w)$. But, as $[X,Y]\in S(Z(A),w)$, by Lemma 3.5$[X\backslash x, Y\backslash x]$ can not be a cell of S(Z(A), w). We conclude that $[X\backslash x, Y\backslash x]^{(k)}$ can not be a cell of $S(A^{(k)},w)$.

Now assume that $k>1$. It is clear that (3)$\Rightarrow$(5)$\Rightarrow$(4). To see that (4)$\Rightarrow$(2) notice that it if $[X\backslash x_i, Y\backslash x_i]^{(k)}\in S(A^{(k)},w)$ holds for $i =1,2$, then the two zonotopes $[X\backslash x_1, Y\backslash x_1]$ and $[X\backslash x_2, Y\backslash x_2]$ are in S(Z(A), w), which can not happen by Lemma 3.5. $\square$

Proposition 3.7

For every configuration A of size n and every $k\in [n-1]$ we have that ${\mathcal {F}}^{(k+1)}(A)$ is a Minkowski summand of

$$\begin{aligned} {\mathcal {F}}^{(k)}(A) + \sum _{i \in [n]} {\mathcal {F}}^{(k)}(A_{[n]\backslash i}). \end{aligned}$$

Proof

That ${\mathcal {F}}^{(k+1)}(A)$ is a Minkowski summand of ${\mathcal {F}}^{(k)}(A) + \sum _{i \in [n]} {\mathcal {F}}^{(k)}(A_{[n]\backslash i})$ is equivalent to: “for every w, if we know the subdivisions that w induces in $A^{(k)}$ and in $A\backslash x^{(k)}$ for every x, then we also know the subdivision induced in $A^{(k+1)}$. For a cell $[X,Y]^{(k+1)}$ with $|X| =k$, Lemma 3.6 says that its presence in $S(A^{(k+1)},w)$ is determined by its presence in $S(A^{(k)},w)$ and $S(A\backslash x^{(k)},w)$. Cells $[X,Y]^{(k+1)}$ with $|X|<k$ are in $S(A^{(k+1)},w)$ if and only if $[X,Y]^{(k)}\in S(A^{(k)},w)$. $\square$

The converse is only true for small k:

Proposition 3.8

For every configuration $A\subseteq {\mathbb {R}}^d$ of size n and every $k\in [d]$ we have that

$$\begin{aligned} {\mathcal {F}}^{(k+1)}(A) \cong {\mathcal {F}}^{(k)}(A) + \sum _{i \in [n]} {\mathcal {F}}^{(k)}(A_{[n]\backslash i}). \end{aligned}$$

Proof

One direction is Proposition 3.7. For the other direction we have that by Lemma 3.6 then $S(A^{(k+1)},w)$ determines $S(A_{[n]\backslash i}^{(k+1)},w)$ for all $i\in [n]$. Any maximal cell in $[X,Y]^{(k)}\in S(A^{(k)},w)$ must satisfy $|Y\backslash X|\ge d+1$, in particular $|Y|\ge d+1> k$, so $[X,Y]^{(k+1)}$ is also a cell in $S(A^{(k+1)},w)$. This implies that $S(A^{(k+1)},w)$ determines $S(A^{(k)},w)$. $\square$

Proposition 3.9

For every configuration $A\subseteq {\mathbb {R}}^d$ of size $n>d+2$ and every $k\in [d]$ we have that

$$\begin{aligned} {\mathcal {F}}^{(k)}(A) \le \sum _{i=1}^n {\mathcal {F}}^{(k)}(A_{[n]\backslash i}) \end{aligned}$$

Proof

We need to prove that for every $w\in {\mathbb {R}}^d$, knowing $S(A_{[n]\backslash i}^{(k)} ,w)$ for every i determines $S(A^{(k)},w)$. It is enough to prove it for a generic w, so we can assume the subdivisions are fine. Let [X, Y] be a tile such that $Y\backslash X$ is an affine basis. We claim that $[X,Y]^{(k)}\in S(A_{[n]\backslash i}^{(k)},w)$ if and only if $[X\backslash i,Y\backslash i]^{(k)}\in S(A_{[n]\backslash i}^{(k)},w)$ for every $i\in [n]\backslash (Y\backslash X)$.

There is exactly one ${\tilde{w}}$ that agrees with w in $\ker (\pi )$ and such that ${\tilde{w}} \cdot x = 0$ for every $x\in Y\backslash X$. We have that $[X,Y]^{(k)}\in S(A_{[n]\backslash i}^{(k)},w)$ if and only if ${\tilde{w}} \cdot x<0$ for every $x \in X$ and $\tilde{w} \cdot x>0$ for every $x \in [n]\backslash Y$. Notice that as $n> d+2$, $|[n]\backslash (Y\backslash X)|> 2$. Let $i \in [n]\backslash (Y\backslash X)$. As $k\le d$ and $|Y\backslash X|= d+1$, then for $Y\backslash i> k$ so $[X\backslash i,Y\backslash i]^{(k)}$ is a full dimensional cell in the level k. So it is in $S(A_{[n]\backslash i}^{(k)},w)$ if and only if $\tilde{w}\cdot x< 0$ for every $x\in X\backslash i$ for all $x \in X\backslash i$ and ${\tilde{w}} \cdot x>0$ for every $x \in [n]\backslash (Y\cup i)$. As $|[n]\backslash (Y\backslash X)|> 2$, we can do this for two different elements in $[n]\backslash (Y\backslash X)$ so we can verify the sign of ${\tilde{w}} \cdot i$ for every $i\in [n]\backslash (Y\backslash X)$. $\square$

A consequence of this is that Proposition 3.8 can be strengthened as follows:

Proposition 3.10

For every configuration $A\subseteq {\mathbb {R}}^d$ of size $n>d+2$ and every $k\in [d]$ we have that

$$\begin{aligned} {\mathcal {F}}^{(k+1)}(A) \cong \sum _{i \in [n]} {\mathcal {F}}^{(k)}(A_{[n]\backslash i}). \end{aligned}$$

Notice that if $n = d+1$ then the fiber polytopes are just points and if $n=d+2$ they are just segments and in particular ${\mathcal {F}}^{(k+1)}(A) \cong {\mathcal {F}}^{(k)}(A)$. Now we are ready to prove the main result of this section:

Theorem 3.11

Let $A\subseteq {\mathbb {R}}^d$ be a configuration of size n and $k\in [d+1]$. Let $s = \max (n-k+1, d+2)$. Then

$$\begin{aligned} {\mathcal {F}}^{(k)}(A) \cong \sum \limits _{J\in {[n]\atopwithdelims ()s}} {\mathcal {F}}(A_J) \end{aligned}$$

Proof

We prove this by iterating Proposition 3.10 several times. At each iteration, for $1<i \le k$, we replace each ${\mathcal {F}}^{(i+1)}(A_J)$ by $\sum \limits _{j \in [n]} {\mathcal {F}}^{(i)}(A_{J\backslash j})$ if $|J| > d+2$ or by ${\mathcal {F}}^{(i)}(A_J)$ if $|J| = d+2$. The iteration stops at level 1 with the desired result (notice that Minkowski sum is idempotent with respect to normal equivalence). $\square$

Example 3.12

The secondary polytope ${\mathcal {F}}^{(1)} (\mathbf {P}_{6})$ of the regular hexagon $\mathbf {P}_{6}$ is the 3-dimensional associahedron, as seen in Fig. 2. Its boundary consists of 6 pentagons and 3 squares. By Theorem 3.11, the hypersecondary polytope ${\mathcal {F}}^{(2)} (\mathbf {P}_{6})$ is normally equivalent to the Minkowski sum of those 6 pentagons, see Fig. 3. It has 66 vertices and the facets consist of 27 quadrilaterals (18 rectangles, 6 rhombi and 3 squares), 6 pentagons, 2 hexagons and 6 decagons. The short edges correspond to flips which do not change the set of vertices of the triangulation and the long edges correspond to those flips that do change the set of vertices.

Fig. 2

The associahedron ${\mathcal {F}}^{(1)}(\mathbf {P}_{6})$

Fig. 3

The hyperassociahedron ${\mathcal {F}}^{(2)}(\mathbf {P}_{6})$

The GKZ vector corresponding to the triangulation from Example 2.9 is in the center of one of the hexagons. There are 4 non-coherent hypertriangulations of $\mathbf {P}_{6}^{(2)}$, which come in pairs with the same GKZ-vector, each in the center of one of the two hexagons. If instead of a regular hexagon we had a hexagon where the three long diagonals do not intersect in the same point, two of those subdivisions would become coherent and the hypersecondary polytope would have instead of each hexagon a triple of rhombi around the new vertex.

The order complex of the Baues poset ${\mathcal {B}}^{(2)}(\mathbf {P}_{6})$ is the (barycentric subdivision of the border of the) hyperassociahedron ${\mathcal {F}}^{(2)}(\mathbf {P}_{6})$ where the hexagons are replaced by cubes. In particular it satisfies the Baues problem, that is, ${\mathcal {B}}^{(2)}(\mathbf {P}_{6})$ retracts onto ${\mathcal {F}}^{(2)}(\mathbf {P}_{6})$. We will generalize this in Sect. 6.

4 Separation and lifting subdivisions

Throughout this section let $A\subset {\mathbb {R}}^d$ be a point configuration labelled by [n], and let $Z(A)\subset {\mathbb {R}}^{d+1}$ be the zonotope generated by the vector configuration $A\times \{1\}\subset {\mathbb {R}}^d\times \{1\}$. Recall that a point in Z(A) is a subset $X\subset [n]$ and a tile is an interval $[X,Y]\subset 2^{[n]}$, where $X\subset Y\subset [n]$.

Following [11], we say that two points $X_1, X_2 \subset [n]$ are separated with respect to A or A-separated for short if there is an affine functional positive on (the elements of A labeled by) ${X_1\backslash X_2}$ and negative on ${X_2\backslash X_1}$. Equivalently, if there is no oriented circuit $(C^+,C^-)$ in A with $C^+\subset X_1\backslash X_2$ and $C^- \subset X_2\backslash X_1$. Their motivation is that the notions of strongly separated and chord separated that were introduced in [14] and [10, 15] are equivalent to “$\mathbf {C}(n,1)$-separated” and “$\mathbf {C}(n,2)$-separated” respectively ( [11, Lemmas 3.7 and 3.10]).¹ One of their main results is as follows (their statement is a bit more general, since it is stated for arbitrary oriented matroids, rather then “point configurations”):

Theorem 4.1

([11, Theorems 2.7 and 7.2]) Let A be a point configuration and let m be the number of affinely independent subsets of A. Then:

• (1) No family of A-separated points in A has size larger than m.

• (2) The map sending each zonotopal tiling to the set of (labelled) points used as vertices gives a bijection

  $$\begin{aligned} \{\text {fine zonotopal tilings of { Z}({ A})}\} \leftrightarrow \{S\subset 2^{[n]} : S \text { is { A}-separated and |S|=m}\}. \end{aligned}$$

We here extend their definition to separation of tiles. In the rest of the paper we omit A and write “separated” instead of A-separated:

Definition 4.2

Let $[X_1,Y_1]$ and $[X_2,Y_2]$ be two tiles. We say they are separated if there is no circuit $(C^+,C^-)$ such that $C^+\subset Y_1\setminus X_2$, $C^-\subset Y_2\setminus X_1$ and $C^+\cup C^- \not \subseteq (Y_1\cap Y_2)\setminus (X_1\cup X_2)$.

The following diagram illustrates the circuits forbidden by the first two conditions in this definition. The third condition forbids circuits with support fully contained in the middle cell:

	$X_2$	$Y_2\setminus X_2$	$[n]\setminus Y_2$
$X_1$	0	$\ge 0$	$\ge 0$
$Y_1\setminus X_1$	$\le 0$	*	$\ge 0$
$[n]\setminus Y_1$	$\le 0$	$\le 0$	0

By the orthogonality between circuits and covectors in an oriented matroid [4, Proposition 3.7.12], and the fact that covectors of a realized oriented matroid are the sign vectors of affine functionals this definition is equivalent to:

Proposition 4.3

Two tiles $[X_1,Y_1]$ and $[X_2,Y_2]$ are separated if there is a covector (that is, an affine functional) that is positive on $(X_1\setminus X_2) \cup (Y_1\setminus Y_2)$, negative on $(X_2\setminus X_1) \cup (Y_2\setminus Y_1)$, and zero on $(Y_1\cap Y_2)\setminus \{X_1\cup X_2\}$.

The following diagram illustrates the sign-patterns of covectors witnessing that two tiles are separated:

	$X_2$	$Y_2\setminus X_2$	$[n]\setminus Y_2$
$X_1$	*	+	+
$Y_1\setminus X_1$	−	0	+
$[n]\setminus Y_1$	−	−	*

Proof

Consider the subset $I=(Y_1\cup Y_2) \setminus (X_1\cap X_2)$ of A, and let $A'$ be the restriction of A to I. Remember that the circuits of $A'$ are the circuits of A with support contained in $A'$, while the covectors of $A'$ are the covectors of A (all of them) restricted to $A'$. In particular, the characterization of covectors of $A'$ as the sign vectors orthogonal to all circuits says that

$$\begin{aligned} \left( (X_1\setminus X_2) \cup (Y_1\setminus Y_2) \, , \, (X_2\setminus X_1) \cup (Y_2\setminus Y_1) \right) \end{aligned}$$

is a covector in $A'$ if and only if a circuit as in the definition of separation does not exist. $\square$

Example 4.4

Two “singleton tiles” (that is, $X_1=Y_1$ and $X_2= Y_2$) are separated as tiles if and only if they are separated as points in the sense of Galashin and Postnikov. Two tiles containing the origin, that is with $X_1=X_2=\emptyset$, are separated if and only if $Y_1$ and $Y_2$ intersect properly in the usual sense, as cells in A (that is to say, ${{\,\mathrm{conv}\,}}(Y_1)\cap {{\,\mathrm{conv}\,}}(Y_2)$ is a common face of ${{\,\mathrm{conv}\,}}(Y_1)$ and ${{\,\mathrm{conv}\,}}(Y_2)$). Finally, the whole zonotope $2^{[n]} = [\emptyset , [n]]$ is separated from a tile [X, Y] if and only if the cells Y and $[n]\setminus X$ intersect properly; this is equivalent to [X, Y] being a face of the zonotope Z(A).

See Example 5.1 for a illustrated example of non-separated tiles. Their restriction to level 2 may be extended to a hypersimplicial subdivision, but the entire tiles intersect each other in the interior.

The following result clarifies the relation between separation of points and tiles. In it, we say that a tile [X, Y] is fine if $Y\backslash X$ is an independent set. Fine tiles are the ones that can be used in fine zonotopal tilings of Z(A).

Proposition 4.5

Let $[X_1,Y_1]$ and $[X_2,Y_2]$ be two tiles. If every point $B_1 \in [X_1,Y_1]$ is separated from every point $B_2 \in [X_2,Y_2]$, then $[X_1,Y_1]$ and $[X_2,Y_2]$ are separated. The converse holds if the tiles are fine.

Proof

We proceed by induction on $|Y_1\backslash X_1| + |Y_2\backslash X_2|$ to prove the first direction. In the base case, when $X_1= Y_1$ and $X_2=Y_2$, the statement holds trivially true since $[X_1,Y_1]$ and $[X_2,Y_2]$ are both single points. So we can assume one of $[X_1,Y_1]$ and $[X_2,Y_2]$, say $[X_1,Y_1]$, is not a singleton. Moreover, by induction hypothesis, we can assume that every tile properly contained in $[X_1,Y_1]$ is separated from $[X_2,Y_2]$. In particular, taking any element $i\in Y_1\backslash X_1$ we have that both $[X_1\cup i,Y_1]$ and $[X_1,Y_1\backslash i]$ are separated from $[X_2,Y_2]$. By Proposition 4.3, that implies the following two covectors:

	$X_2$	$Y_2\backslash X_2$	$[n]\backslash Y_2$
$X_1$	*	+	+
i	*	+	+
$Y_1\backslash X_1 \backslash i$	−	0	+
$[n]\setminus Y_1$	−	−	*

	$X_2$	$Y_2\backslash X_2$	$[n]\backslash Y_2$
$X_1$	*	+	+
$Y_1\backslash X_1 \backslash i$	−	0	+
i	−	−	*
$[n]\setminus Y_1$	−	−	*

If $i\in X_2$ or $i\in [n]\backslash Y_2$ then the first or the second covector, respectively, show that $[X_1,Y_1]$ and $[X_2,Y_2]$ are separated. If $i\in Y_2\backslash X_2$ then elimination of i in these two covectors gives a covector with values

	$X_2$	$Y_2\backslash X_2$	$[n]\backslash Y_2$
$X_1$	*	+	+
i		0
$Y_1\backslash X_1 \backslash i$	−	0	+
$[n]\setminus Y_1$	−	−	*

which again shows that $[X_1,Y_1]$ and $[X_2,Y_2]$ are separated.

For the converse, suppose that $[X_1,Y_1]$ and $[X_2,Y_2]$ are fine and separated. Let V be the covector showing it. Let $B_1$ and $B_2$ be points in them. Since the set $C{:}{=}(Y_1\setminus X_1) \cap (Y_2 \setminus X_1)$ is independent and is contained in the zero-set of V, no matter what signs we prescribe for its elements there is a covector $V'$ that agrees with V where V is not zero and has the prescribed signs on C. This implies the points $B_1$ and $B_2$ are separated. $\square$

Theorem 4.6

Let $[X_1,Y_1]$ and $[X_2,Y_2]$ be two tiles. Then, the following conditions are equivalent:

• (1) The tiles are separated.

• (2) There is a zonotopal tiling of Z(A) using both.

• (3) There is a coherent zonotopal tiling of Z(A) using both.

• (4) There is a polyhedral subdivision of A using $Y_1\backslash X_2$ and $Y_2\backslash X_1$ as cells.

• (5) There is a coherent polyhedral subdivision of A using $Y_1\backslash X_2$ and $Y_2\backslash X_1$ as cells.

Remark 4.7

For the case of general subdivisions of a point configuration A implication $2\Rightarrow 3$ is well known (see [8, Exercise 2.5]. An alternative proof for zonotopes is to transfer that case via the Cayley Trick ([8, Corollary 9.2.19]).

Proof

Throughout the proof, let $A=\{a_1,\dots ,a_n\}$ and denote $\tilde{a}_i =(a_i,1)$ the corresponding generator of Z(A).

• $1\Rightarrow 3$. Suppose the tiles are separated. By Proposition 4.3 this implies there is a linear functional $v\in ({\mathbb {R}}^{d+1})^*$ such that $v\cdot {\tilde{a}}_i$ takes the following values on the generators of Z(A):

	$X_2$	$Y_2\setminus X_2$	$[n]\setminus Y_2$
$X_1$	*	$>0$	$>0$
$Y_1\setminus X_1$	$<0$	0	$>0$
$[n]\setminus Y_1$	$<0$	$<0$	*

Let $w\in ({\mathbb {R}}^n)^*$ be defined as follows on each $i\in [n]$:

	$X_2$	$Y_2\setminus X_2$	$[n]\setminus Y_2$
$X_1$	$-N$	$-2\, v\cdot {\tilde{a}}_i$	$-v\cdot {\tilde{a}}_i$
$Y_1\setminus X_1$	0	0	0
$[n]\setminus Y_1$	$-v\cdot {\tilde{a}}_i$	$-2\,v\cdot {\tilde{a}}_i$	$+N$

where N is a very large positive number. Since w is negative in $X_1$, positive in $[n]\backslash Y_1$, and zero in $Y_1\backslash X_1$, the tile selected by w in the subdivision S(Z(A), w) is $[X_1,Y_1]$. Similarly, the vector ${w'}\in ({\mathbb {R}}^n)^*$ defined by ${w'}_i = w_i +2 v\cdot {\tilde{a}}_i$ has the following values

	$X_2$	$Y_2\setminus X_2$	$[n]\setminus Y_2$
$X_1$	$<0$	0	$v\cdot {\tilde{a}}_i$
$Y_1\setminus X_1$	$2\,v\cdot {\tilde{a}}_i$	0	$2\,v\cdot {\tilde{a}}_i$
$[n]\setminus Y_1$	$v\cdot {\tilde{a}}_i$	0	$>0$

which shows that $[X_2,Y_2]$ is also in S(Z(A), w), since the difference between w and $w'$ is a linear function.

• $2\Rightarrow 1$. By the Bohne-Dress Theorem, zonotopal tilings of Z(A) correspond to lifts of the oriented matroid of Z(A). Here, a lift is an oriented matroid ${\mathcal {M}}$ of rank $d+2$ on the ground set $[n+1]$ and such that ${\mathcal {M}}/(n+1) ={\mathcal {M}}(A)$. The tiles of the subdivision defined by the lift ${\mathcal {M}}$ are the intervals $[X,Y]\subset 2^{[n]}$ such that ${\mathcal {M}}$ has a covector that is negative on X, zero on $Y\setminus X$, and positive on $[n+1] \backslash Y$. That is, our hypothesis is that there is a lift ${\mathcal {M}}$ of A that contains the covectors

  $$\begin{aligned} ([n+1] \setminus Y_1 \, ,\, X_1) \qquad \text { and }\qquad (X_2\, ,\, [n+1] \setminus Y_2). \end{aligned}$$

  Elimination of the element $n+1$ among these covectors gives us a covector of Proposition 4.3.

• $1\Rightarrow 5$. Let v as in the proof of $1\Rightarrow 3$, and define $w\in ({\mathbb {R}}^n)^*$ as follows:

	$X_2$	$Y_2\setminus X_2$	$[n]\setminus Y_2$
$X_1$	N	0	0
$Y_1\setminus X_1$	$-v\cdot {\tilde{a}}_i$	0	0
$[n]\setminus Y_1$	$-v\cdot {\tilde{a}}_i$	$-v\cdot {\tilde{a}}_i$	N

Then w and the $w'$ defined by $w'_i = w_i + v\cdot {\tilde{a}}_i$ show that $Y_1\backslash X_2$ and $Y_2\backslash X_1$ are cells in S(A, w).

• $4\Rightarrow 1$ For $C_1{:}{=}Y_1\backslash X_2$ and $C_2{:}{=}Y_2\backslash X_1$ to be cells in a subdivision it is necessary that their convex hulls intersect in a common face. That is, there must be a covector in A that is zero in $C_1\cap C_2$, negative on $C_1\setminus C_2$, and positive on $C_2\setminus C_1$. These are precisely the same conditions as required in Proposition 4.3.

• $3\Rightarrow 2$ and $5\Rightarrow 4$ are obvious.

$\square$

Remark 4.8

With this theorem, it is now easy to see that Lemma 3.5 also holds for non coherent subdivisions. If $Y_1\backslash X_1 = Y_2\backslash X_2$ is a spanning set then there can not be a linear functional vanishing on it, so $[X_1,Y_1]$ and $[X_2,Y_2]$ are not separated (unless $X_1 = X_2$, in which case they are the same cell).

Remark 4.9

The definition of separated points and tiles makes sense for an arbitrary oriented matroid ${\mathcal {M}}$, since it uses only the notion of circuits, and Proposition 4.3 still holds in this more general setting.

The notions of zonotopal tiling and of subdivision also make sense for arbitrary oriented matroids: the former is interpreted as “extension of the dual oriented matroid” via Theorem 2.11 and the latter is studied in detail in [21]. In this setting the implications $(2) \Rightarrow (4) \Rightarrow (1)$ of Theorem 4.6 still hold, the first one as a consequence of the oriented matroid analogue of Proposition 2.10 and the second one because our proof above works at the level of oriented matroids. Yet:

• (1) The converse implications do not hold in the nonrealizable case. The implication $(4) \Rightarrow (2)$ fails in the example of [21, Section 5.2] (see Proposition 5.6(i) in that section), and the implication $(1) \Rightarrow (4)$ fails in the Lawrence polytope that one can construct from that example.

• (2) The notion of coherent subdivisions does not make sense for nonrealizable oriented matroids. Moreover, for realizable ones, different realizations of the same oriented matroid may have different sets of coherent subdivisions, and non-isomorphic secondary polytopes/zonotopes.

Corollary 4.10

Let $[X_1,Y_1]$ and $[X_2,Y_2]$ be two separated tiles. Then any pair of subtiles $[\tilde{X_1},\tilde{Y_1}]\subseteq [X_1,Y_1]$ and $[\tilde{X_2},\tilde{Y_2}]\subseteq [X_2,Y_2]$ are separated.

Proof

By Theorem 4.6, there is a zonotopal tiling using $[X_1,Y_1]$ and $[X_2,Y_2]$ and such tiling uses $[\tilde{X_1},\tilde{Y_1}]$ and $[\tilde{X_2},\tilde{Y_2}]$. $\square$

Proposition 4.11

Let A be a configuration of n pairwise independent points. Let $k\in [n-1]$. Let $[X_1,Y_1]$ and $[X_2,Y_2]$ be two tiles that cover level k (that is, $|X_i|< k < |Y_i|)$. Suppose that $[X_1,Y_1]$ and $[X_2,Y_2]$ are not-separated and that one of them is not fine.

Then, there are fine tiles $[X'_1,Y'_1]$ and $[X'_2,Y'_2]$ contained in $[X_1,Y_1]$ and $[X_2,Y_2]$, still covering level k and still not separated.

Proof

By induction on the dependence rank (that is, $|Y\backslash X| - \dim ({\text {span}}(Y\backslash X))$) of the tiles we only need to show that if $[X_1,Y_1]$ is dependent then there is a tile $[X'_1,Y'_1]$ properly contained in $[X_1,Y_1]$, covering level k, and non-separated from $[X_2,Y_2]$.

Let $(C_+,C_-)$ be a circuit showing that $[X_1,Y_1]$ and $[X_2,Y_2]$ are not-separated. Let $C=C_+\cup C_-$ be its support.

If there is an element $a\in (Y_1\backslash X_1) \backslash C$ then both $[X_1\cup a, Y_1]$ and $[X_1, Y_1\backslash a]$ are not separated from $[X_2,Y_2]$, and one of them still covers level k, since dependent sets are of size at least 3.

If there is no such an a, then $Y_1\backslash X_1 \subset C$. Since C is a circuit we conclude that $Y_1\backslash X_1 = C$. By definition, we have that $C_- \subset Y_2$ and $C_+ \subset [n]\backslash X_2$. Again, we take as new tile $[X_1\cup a, Y_1]$ or $[X_1, Y_1\backslash b]$, depending on which of the two still covers level k, where $a \in C_+$ and $b\in C_-$. $\square$

Corollary 4.12

Let A be a point configuration in general position (“uniform”) and let $k\in [n-1]$. If no hypertriangulation of $A^{(k)}$ contains two non-separated tiles, then no hypersimplicial subdivision of $A^{(k)}$ contains them either.

Proof

Suppose that a subdivision S contains two non-separated tiles $[X_1,Y_1]$ and $[X_2,Y_2]$. Let $[X'_1,Y'_1]$ and $[X'_2,Y'_2]$ be the tiles guaranteed by Proposition 4.11. Then, we can refine $[X_1,Y_1]$ and $[X_2,Y_2]$ to fine subdivisions using $[X'_1,Y'_1]$ and $[X'_2,Y'_2]$. By general position this extends to a hypertriangulation refining S and with two non-separated tiles. $\square$

5 Non-separated subdivisions

We call a subdivision S of $A^{(k)}$ non-separated if it contains two non-separated cells. Non-separated subdivisions are certainly non-lifting, by the implication $(2)\Rightarrow (1)$ in Theorem 4.6.

Example 5.1

We here construct a non-separated subdivision in dimension two, which contrasts the fact that for $\mathbf {P}_{n}$ such things do not exist [6]. Let A be the configuration of the following 5 points in the plane: $p_1 = (1,2)$, $p_2 = (0,4)$, $p_3 = (4,4)$, $p_4 = (4,0)$ and $p_5 = (0,0)$. Figure 4 on the right shows a hypertriangulation of $A^{(2)}$ consisting of the triangles:

$$\begin{aligned}&[\emptyset ,234]^{(2)}, [\emptyset ,245]^{(2)},\\&[2,1235]^{(2)},[2,2345]^{(2)},[4,1234]^{(2)},[4,1245]^{(2)},[4,1345]^{(2)},[5,1245]^{(2)}. \end{aligned}$$

The circuit (14, 35) shows that the cell $[2,2345]^{(2)}$ is not separated from the cells $[4,1234]^{(2)}$ and $[4,1245]^{(2)}$.

Fig. 4

A not separated hypertriangulation in the plane

The following non-separated subdivision of $\mathbf {C}(4,1)^{(2)}$ appears as Example 10.4 in [17]:

$$\begin{aligned} S=\{ [1,123]^{(2)}, [1,134]^{(2)}, [4,124]^{(2)}, [4,234]^{(2)} \}. \end{aligned}$$

Here we generalize it to

Lemma 5.2

For every odd d and every $k\in [2,d-2]$ there is a non-separated hypertriangulation of $\mathbf {C}(d+3,d)^{(k)}$.

Proof

A hypertriangulation of a configuration A with $n=d+3$ has all its full-dimensional cells of one of the following forms, where $a < b\in [n]$ and we omit the superscript (k), which will be clear from the context:

$$\begin{aligned} {[\,\emptyset , \ [n]\backslash ab\,]}, \quad {[\,a, \ [n]\backslash b\,]},\quad {[\,b, \ [n]\backslash a\,]},\quad {[\,ab, \ [n]\,]}. \end{aligned}$$

To simplify notation, we denote these four cells simply as ab, ${\overline{a}} b$, $a {\overline{b}}$ and ${\overline{a}} {\overline{b}}$, respectively (observe that we always write the indices a and b in increasing order). For example, in this notation the subdivision S of $\mathbf {C}(4,1)^{(2)}$ mentioned above becomes

$$\begin{aligned} S=\{ {\overline{1}}4, {\overline{1}}2, 3{\overline{4}}, 1{\overline{4}} \}^{(2)}. \end{aligned}$$

One reason for this notation is that via the correspondence in Proposition 2.10 the tile [X, Y] corresponds in $\mathbf {G}_{A}$ to the cone spanned by $X\cup \overline{[n]\setminus Y}$, where we use $\overline{B}$ to denote the set of vectors opposite to B, for $B\subset [n]$.

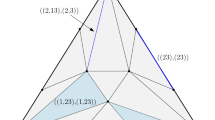
With this notation, Proposition 2.10(2) gives us that the following is a (coherent) zonotopal tiling of $Z(\mathbf {C}(d+3,d))$ (Fig. 5 shows the case of $\mathbf {C}(6,3)$):

$$\begin{aligned} S_0 {:}{=}&\{{\overline{a}}b: a \text { odd}, b \text { odd}\}\cup \{{\overline{a}}{\overline{b}}: a \text { odd}, b \text { even}\}\\&\cup \{ab: a \text { even}, b \text { odd}\}\cup \{a {\overline{b}}: a \text { even}, b \text { even}\}. \end{aligned}$$

Fig. 5

The Gale transform of $\mathbf {C}(6,3)$, with the regions corresponding to the zonotopal tilings $S_0$, $S_1$ and $S_2$ marked in it

Recall that a cubical flip in a zonotopal tiling consists in replacing a collection of tiles that cover the projection of a $(d+1)$-dimensional face F of $[0,1]^n$ by the projection of all other facets of F (in analogy with flips of triangulations that do the same with a face of the simplex instead of the cube). $S_0$ admits the following cubical flips:

• Flip 1: negate the other symbol in every cell containing ${\overline{1}}$. That is, remove

  $$\begin{aligned} \{{\overline{1}}b: b>1 \text { odd}\}\cup \{{\overline{1}}{\overline{b}}: b \text { even}\} \end{aligned}$$

  and insert

  $$\begin{aligned} \{{\overline{1}}{\overline{b}}: b>1 \text { odd}\}\cup \{{\overline{1}} b: b \text { even}\}. \end{aligned}$$

• Flip 2: negate the other element in every cell containing ${\overline{n}}$. That is, remove

  $$\begin{aligned} \{a {\overline{n}}: a<n \text { even}\}\cup \{{\overline{a}}{\overline{n}}: a \text { odd}\} \end{aligned}$$

  and insert

  $$\begin{aligned} \{{\overline{a}} {\overline{n}}: a<n \text { even}\}\cup \{ a{\overline{n}}: a \text { odd}\}. \end{aligned}$$

These flips transform $S_0$ into two new coherent tilings $S_1$ and $S_2$, also shown in Fig. 5. The two flips are not compatible, since both want to remove the tile $\overline{1}\overline{n}$ from $S_0$, and we can only remove it once. But $\overline{1}{\overline{n}}$ only affects level 1 of the tiling, which means that in any $S_0^{(k)}$ with $k\ge 2$ we can do these two flips one after the other. After performing them we get a subdivision that contains (for $k\in [2,d-2]$) the non-separated cells

$$\begin{aligned} \overline{1} 2 \qquad \text {and}\qquad n-1 {\overline{n}}. \end{aligned}$$

$\square$

To further generalize this construction we need the following easy lemma:

Lemma 5.3

Let A be a d-dimensional configuration of size n in general position. If $A_{[n]\backslash i}^{(k)}$ has a non-separated subdivision S for some $i\in [n]$ then $A^{(k)}$ and $A^{(k+1)}$ have non-separated subdivisions too.

Proof

For $A^{(k)}$ do the following: Extend S to a subdivision $S'$ of A by adding all the cells of the form $[X, Y\cup i]^{(k)}$ with $[X,Y] \subset 2^{[n]}$ such that ${[X, Y\cup i]}$ is separated from $[\emptyset , [n]\backslash i]$. (The latter is equivalent to saying that [X, Y] is contained in a facet of $Z(A_{[n]\backslash i})$ whose normal vector has positive scalar product with i). $S'$ is non-separated since it contains S.

For $A^{(k+1)}$ apply the same construction upside-down. That is, consider the non-separated subdivision ${\overline{S}}$ of $A_{[n]\backslash i}^{(n-k-1)}$ obtained from S via the map $[X,Y] \rightarrow [[n]\backslash Y,[n]\backslash X]$. From ${\overline{S}}$ construct a non-separated subdivision $\overline{S'}$ of $A^{(n-k-1)}$ as above, then turn $\overline{S'}$ upside-down to get a non-separated subdivision of $A^{(k+1)}$. $\square$

Corollary 5.4

For every odd d, every $n\ge d+3$, and every $k\in [2,n-2]$, there is a non-separated hypertriangulation of $\mathbf {C}(n,d)^{(k)}$. $\square$

Question 5.5

Are there non separated hypertriangulations of $\mathbf {C}(n,d)^{(k)}$ for $d\ge 4$ even? The case of $\mathbf {C}(n,2)$ suggests that the answer is no.

6 Baues posets of $\mathbf {P}_{n}$

6.1 Preliminaries and notation

In this section we are interested in the case when A is a convex polygon $\mathbf {P}_{n}$, and we make use of the fact that all hypersimplicial subdivisions are lifting. We first introduce the following notation, for general A:

Definition 6.1

Let A be a configuration and let S be a zonotopal tiling of Z(A). We define $S^{(k+\frac{1}{2})}$ as the set of tiles that cover levels k and $k+1$. That is:

$$\begin{aligned} S^{(k+\frac{1}{2})}&{:}{=} \{[X,Y]\in S : |X| < k, |Y| > k+1 \}. \end{aligned}$$

Observe that a lifting subdivision of $A^{(k)}$ may have several extensions to a zonotopal tiling of Z(A). However, the following holds:

Proposition 6.2

Let S and $S'$ be zonotopal tilings of Z(A) with the same restriction $S^{(k)} = S'^{(k)}$. Then, $S^{(k+\frac{1}{2})}= S'^{(k+\frac{1}{2})}$ and $S^{(k-\frac{1}{2})}= S'^{(k-\frac{1}{2})}$.

Proof

Both $S^{(k+\frac{1}{2})}$ and $S^{(k-\frac{1}{2})}$ contain only tiles of S that cover level k, and those appear as full-dimensional cells in $S^{(k)} = S'^{(k)}$. $\square$

The proposition suggests we define the following poset and maps:

Definition 6.3

Let

$$\begin{aligned} {\mathcal {B}}^{(k+\frac{1}{2})}(\mathbf {P}_{n}) {:}{=} \{S^{(k+\frac{1}{2})} : S \in {\mathcal {B}}^Z(\mathbf {P}_{n})\}, \end{aligned}$$

partially ordered by refinement: $S_1 < S_2$ if and only if $\forall \sigma \in S_1 \exists \tau \in S_2: \sigma \subseteq \tau$. By Proposition 6.2 and the fact that all hypersimplicial subdivisions of $\mathbf {P}_{n}$ are lifting, [6] we have two order-preserving maps

$$\begin{aligned} {\mathcal {U}}&: {\mathcal {B}}^{(k)}(\mathbf {P}_{n}) \rightarrow {\mathcal {B}}^{(k+\frac{1}{2})}(\mathbf {P}_{n}) , \\ {\mathcal {D}}&: {\mathcal {B}}^{(k+1)}(\mathbf {P}_{n}) \rightarrow {\mathcal {B}}^{(k+\frac{1}{2})}(\mathbf {P}_{n}) \end{aligned}$$

defined as

$$\begin{aligned} {\mathcal {U}}(S^{(k)}) = {\mathcal {D}}(S^{(k+1)}) {:}{=} \{[X,Y] : {[X,Y]} \in {S},\ |X| < k \text { and } |Y| > k+1\} . \end{aligned}$$

By construction, we have the following commutative diagram, in which $r^{(k)}$ and $r^{(k+1)}$ are the maps of Proposition 2.8:

Notice that the four maps are surjective: $r^{(k)}$ and $r^{(k+1)}$ are surjective because all hypersubdivisions of $\mathbf {P}_{n}$ are lifting. On the other hand, ${\mathcal {D}}\circ r^{(k+1)} = {\mathcal {U}}\circ r^{(k)}$ is surjective (and hence ${\mathcal {D}}$ and ${\mathcal {U}}$ are surjective too) by definition.

Remark 6.4

For a non-lifting hypersimplicial subdivision S of a general configuration $A^{(k)}$ (resp., of $A^{(k+1)}$) it still makes sense to define ${\mathcal {U}}(S)$ (resp., ${\mathcal {D}}(S)$) as the collection of cells in S whose corresponding tiles in Z(A) cover both the levels k and $k+1$. One can then define ${\mathcal {B}}^{(k+\frac{1}{2})}(A)$ as the union ${\mathcal {U}}({\mathcal {B}}^{(k)}(A)) \cup {\mathcal {D}}({\mathcal {B}}^{(k+1)}(A))$ (or any natural poset containing this union) and get the same diagram as above, but none of the maps is guaranteed to be surjective anymore. Surjectivity is crucial for what we want to do, since it is needed in our main technical tool Lemma 6.10.

Fig. 6

The subdivision $T\in {\mathcal {B}}^{(2)}(\mathbf {P}_{6})$ of Example 6.5 (left) and the first level of ${{\mathcal {D}}(T)}$ (right)

Example 6.5

Consider the subdivision $T\in {\mathcal {B}}^{(2)}(\mathbf {P}_{6})$ in Fig. 6 whose maximal cells are

$$\begin{aligned} \left\{ [\emptyset , 124]^{(2)}, [\emptyset ,234]^{(2)},[\emptyset ,1456]^{(2)},[1,1246]^{(2)},[2,1234]^{(2)},[4,1345]^{(2)},[4,2345]^{(2)}\right\} \end{aligned}$$

The gray cells of T in the figure give ${\mathcal {D}}(T)$; that is:

$$\begin{aligned} {\mathcal {D}}(T) = \{[\emptyset , 124],[\emptyset ,234],[\emptyset ,1456]\}. \end{aligned}$$

As seen in the right part of the figure, the cells in ${\mathcal {D}}(T)$ are precisely the ones that have a full-dimensional intersection with the first level.

Proposition 6.6

Let $S\in {\mathcal {B}}^{(k+\frac{1}{2})}(\mathbf {P}_{n})$. Consider a point $X\in {{\,\mathrm{vertices}\,}}(S^{(k)})$. Define

$$\begin{aligned} {{\,\mathrm{uh}\,}}_S(X) {:}{=} X \cup \{i\in [n] : X\cup i \in {{\,\mathrm{vertices}\,}}(S^{(k+1)})\}. \end{aligned}$$

(Here “ ${{\,\mathrm{uh}\,}}$” stands for “upper hole”). Then $[X,{{\,\mathrm{uh}\,}}_S(X)]$ is separated from every cell in S.

Proof

Observe that ${{\,\mathrm{uh}\,}}_S(X)$ equals

$$\begin{aligned} \{i\in [n] : \exists j\in X \quad [X\setminus j, X\cup i] \text { is a face of a cell in } S\}. \end{aligned}$$

Suppose there exist $X\in {{\,\mathrm{vertices}\,}}(S^{(k)})$ and $[I,J]\in S$ such that $[X, \cup {{\,\mathrm{uh}\,}}_S(X)]$ and [I, J] are not separated. Since $d=2$ we may assume that $|J\setminus I| \le 2$ and there is $Y\in [X, {{\,\mathrm{uh}\,}}_S(X)]^{(k+2)}$ such that [X, Y] is not separated from [I, J]. So we have a circuit $(C^+, C^-)$ such that $C^+\in Y\setminus I$ and $C^-\in J\setminus X$ Further, since $S\in {\mathcal {B}}^{(k+\frac{1}{2})}(\mathbf {P}_{n})$ we can also assume $|I|\le k-1$. Let $y\in Y\setminus X$. Since $y\in {{\,\mathrm{uh}\,}}_S(X)\setminus X$ we have that there is $x\in X$ such that $[X\setminus x, X\cup y]$ is a face of a cell in S. Then by Proposition 4.10 and the fact that S is pairwise separated we have that $[X\setminus x, X\cup y ]$ is separated from [I, J]. So $C^+$ can not be contained in $X\cup y$. This means that $C^+ = Y\setminus X$. Notice that for every $i \in [n] \setminus C$ there is $y\in C^+$ such that $(C^+\setminus y \cup i, C^-)$ is a circuit. So if there is an $i \in X\setminus I$, this circuit would imply that $[X, Y\setminus y ]$ is not separated from [I, J], which can not be as $[X, Y\setminus y]$ is a face of some cell in S. But this means $X\setminus I = \emptyset$ which is a contradiction since $|X|= k > k-1 = |I|$. $\square$

6.2 Hypercatalan numbers

Although this is not needed for the main result on Baues posets, let us see how the upper holes ${{\,\mathrm{uh}\,}}_S(X)$ defined in Proposition 6.6 allow us to count hypertriangulations of a polygon at level two.

Let $C_n^{(k)}$ be the number of hypertriangulations of $\mathbf {P}_{n+2}^{(k)}$. E.g., $C_n^{(1)}$ is the Catalan number $C_n$. For a triangulation T of $\mathbf {P}_{n+2}$ and a vertex $i\in [n+2]$ we write $\deg _T(i)$ for the number of diagonals (edges excluding the sides of $\mathbf {P}_{n+2}$) in T incident to i. We call it the degree of i in T.

Lemma 6.7

$$\begin{aligned} C_n^{(2)} = \sum _T \prod _{i\in [n+2]} C_{\deg _T(i)}, \end{aligned}$$

where the sum runs over all trinangulations T of $\mathbf {P}_{n+2}$.

Proof

Let T be a triangulation of $\mathbf {P}_{n+2}$. To get a hypertriangulation of $\mathbf {P}_{n+2}^{(2)}$ that agrees with T we need to triangulate $[i,{{\,\mathrm{uh}\,}}_T(i)]^{(2)}$ for every i. As $[i,{{\,\mathrm{uh}\,}}_T(i)]^{(2)}$ is a polygon with $\deg _T(i)+2$ vertices, the number of ways to triangulate it is $C_{\deg _T(i)}$. So, for each triangulation T there are $\prod \limits _{i\in [n+2]} C_{\deg _T(i)}$ hypertriangulations of $\mathbf {P}_{n+2}^{(2)}$. Summing over all triangulations gives the desired result. $\square$

Thus, in order to compute or bound $C_n^{(2)}$ we need to understand how degrees are distributed in triangulations. The following result summarizes what we need:

Lemma 6.8

Let T be a triangulation of $\mathbf {P}_{n+2}$ and let $n_i$ denote the number of vertices of degree i in T. Then:

• (1) $\sum _{i\in [n+2]} {\deg _T(i)} = 2n-2$.

• (2) If $n\ge 2$ then $2 \le n_0 \le \frac{n+2}{2}$.

• (3) If $n\ge 4$ then $3n_0 + n_1 \le \frac{3}{2}(n+2)$.

Proof

For part (1) just observe that $\sum _{i\in [n+2]} {\deg _T(i)}$ equals twice the number of interior diagonals in T, which is $n-1$. Part (2) is well-known, since $n_0$ is the number of ears in T.

For part (3), let T be a triangulation maximizing $3n_0+n_1$ and, among those, maximizing $n_0$. If some vertex i of degree 1 is not adjacent to an ear, flipping this edge would increase $n_0$ by one and decrease $n_1$ by at most three (at vertices $i-1$, i and $i+1$; the fourth vertex of the flipped quadrilateral must have degree at least two before the flip and it increases its degree by the flip).

So, in T every vertex of degree 1 is next to an ear. Moreover, such a vertex cannot be next to two ears (for then our polygon would be a quadrilateral, $n=2$) and it cannot be next to another vertex of degree one (for then our polygon would be a pentagon, $n=3$). That is to say, all vertices of degree one belong to a pair (ear,degree 1) separated from the rest of the polygon by a diagonal. Let $n_0'$ be the number of extra ears, not adjacent to any vertex of degree 1. Then $n_0-n_0' = n_1$ is the number of pairs (ear, degree 1) and we have:

$$\begin{aligned} n_1+3n_0 \le \frac{3}{2}(n_1+2n_0) = \frac{3}{2} (3n_1+2n_0') \le \frac{3}{2}(n+2). \end{aligned}$$

$\square$

Corollary 6.9

Let $n\ge 4$. For every triangulation T of the $(n+2)$-gon we have

$$\begin{aligned} 2^{n-2} \le \prod _{i\in [n+2]} C_{\deg _T(i)} \le 2^{\frac{5}{2}n -7}. \end{aligned}$$

Hence,

$$\begin{aligned} 2^{n-2} \le \frac{C_n^{(2)}}{C_n} \le 2^{\frac{5}{2}n -7}. \end{aligned}$$

$\square$

Proof

Since $C_0=C_1=1$, we have

$$\begin{aligned} \prod _{i\in [n+2]} C_{\deg _T(i)} = \prod _{\deg _T(i)\ge 1} C_{\deg _T(i)} = \prod _{\deg _T(i)\ge 2} C_{\deg _T(i)}. \end{aligned}$$

Then, using that $C_k\ge 2^{k-1}$ for $k\ge 1$ and parts (1) and (2) of Lemma 6.8 we get:

$$\begin{aligned} \prod _{\deg _T(i)\ge 1} C_{\deg _T(i)} \ge&\prod _{\deg _T(i)\ge 1} 2^{\deg _T(i)-1} \\ =&2^{n_0}\prod _{i\in [n+2]} 2^{\deg _T(i)-1} = 2^{n_0}2^{n-4} \ge 2^{n-2}. \end{aligned}$$

Similarly, using $C_k\le 2^{2k-3}$ for $k\ge 2$ and parts (1) and (3) of the lemma:

$$\begin{aligned} \prod _{\deg _T(i)\ge 2} C_{\deg _T(i)} \le&\prod _{\deg _T(i)\ge 2} 2^{2\deg _T(i)-3} \\ =&2^{n_1+3n_0}\prod _{i\in [n+2]} 2^{2\deg _T(i)-3}= 2^{n_1+3n_0} \, 2^{n-10} \le 2^{\frac{5}{2}n-7}. \end{aligned}$$

$\square$

We have evaluated the formula of Lemma 6.7 for $n \le 8$. On the other hand, since all hypertriangulations of a polygon are lifting, every $C_n^{(k)}$ is bounded from above by the number of fine zonotopal tilings of $Z(\mathbf {P}_{n+2})$, which is known for $n+2\le 7$ (sequence A060595 in the Online Encyclopedia of Integer Sequences). The following table compares all these numbers.

$n+2$	3	4	5	6	7	8	9	10
${C_n}$	1	2	5	14	42	132	429	1430
$C_n^{(2)}$	1	2	10	70	574	5176	49656	497640
$C_n^{(2)}/C_n$	1	1	2	5	13.67	39.21	115.75	348
A060595	1	2	10	148	7686

6.3 Proof of the main result

In this section we prove that the maps ${\mathcal {U}}$ and ${\mathcal {D}}$ of Definition 6.3 induce homotopy equivalences of the corresponding order complexes (Corollary 6.16). From this we will derive that the inclusion ${\mathcal {B}}_{{{\,\mathrm{coh}\,}}}^{(k)}(\mathbf {P}_{n}) \rightarrow {\mathcal {B}}^{(k)}(\mathbf {P}_{n})$ and the restriction $r^{(k)}: {\mathcal {B}}^Z(\mathbf {P}_{n}) \rightarrow {\mathcal {B}}^{(k)}(\mathbf {P}_{n})$ are also homotopy equivalences (Theorem 6.17 and Corollary 6.18).

To prove this we use the following criterion, which was originally proved by Babson [1]. Another proof can be found in [23] and some generalizations appear in [7]. Recall that we call a poset contractible if its order complex is contractible.

Lemma 6.10

(Babson’s Lemma) Let $f: {\mathcal {P}} \rightarrow {\mathcal {Q}}$ be an order preserving map between two posets. Suppose that for every $q\in {\mathcal {Q}}$ we have that

• (1) $f^{-1}(q)$ is contractible, and

• (2) $f^{-1}(q) \cap {\mathcal {P}}_{\le p}$ is contractible, for every $p\in f^{-1}({\mathcal {Q}}_{\ge q})$.

Then f is a homotopy equivalence.

Observe that part (1) needs the map f to be surjective, since the empty poset is not contractible. In our case surjectivity comes from the fact that all hypersimplicial subdivisions of $\mathbf {P}_{n}$ are lifting ( [6, Lemma 6.3], see Remark 6.4).

For a collection S of tiles of Z(A), let ${{\,\mathrm{vertices}\,}}(S^{(k)})$ be the set of vertices of cardinality k of all zonotopes in S, that is, the vertices of all the cells in $S^{(k)}$. Recall that we only consider a point B in [X, Y] to be a vertex if it is a face; that is, if [X, Y] is separated from $\{B\}$.

Proposition 6.11

Let $S\in {\mathcal {B}}^{(k+\frac{1}{2})}(\mathbf {P}_{n})$. Then

$$\begin{aligned} S^{(k+1)}\cup \{[X, {{\,\mathrm{uh}\,}}_S(X)]^{(k+1)} : X \in {{\,\mathrm{vertices}\,}}(S^{(k)}) \}, \end{aligned}$$

together with all their faces, form the unique coarsest subdivision in the fibre ${\mathcal {D}}^{-1}(S)$.

Proof

Every cell in a subdivision of $\mathbf {P}_{n}^{(k+1)}$ containing S that is not already in S is of type 1. Hence it is of the form $[X,Y]^{(k+1)}$ for a vertex $X\in {{\,\mathrm{vertices}\,}}(S^{(k)})$. By Proposition 6.6, the tiles $[X, {{\,\mathrm{uh}\,}}_S(X)]$ are separated from each other, so we only need to prove that for $X_1, X_2\in {{\,\mathrm{vertices}\,}}(S^{(k)})$, $[X_1,{{\,\mathrm{uh}\,}}_S(X_1)]$ and $[X_2,{{\,\mathrm{uh}\,}}_S(X_2)]$ are separated. To show this, suppose they were not. Then, we can again assume there are subsets $Y_1\subseteq {{\,\mathrm{uh}\,}}_S(X_1)$ and $Y_2 \subseteq {{\,\mathrm{uh}\,}}_S(X_2)$ of cardinality $k+2$ such that $[X_1, Y_1]$ and $[X_2,Y_2]$ are separated. As all subtiles of them are faces of S, we have that there is a circuit $C^+ = Y_1\setminus X_1$ and $C^-= Y_2\setminus X_2$. As in the proof of Proposition 6.6, this implies that $X_1 = X_2$. The corollary follows from the fact that every cell in a subdivision in ${\mathcal {D}}^{-1}(S)$ not coming from S is contained in $[X,{{\,\mathrm{uh}\,}}_S(X)]$ for some X. $\square$

Example 6.12

Consider the subdivision $S\in {\mathcal {B}}^{(1)}(\mathbf {P}_{6})$ in Fig. 7 whose maximal cells are

$$\begin{aligned} \left\{ [\emptyset , 124]^{(1)}, [\emptyset ,234]^{(1)},[\emptyset ,145]^{(1)},[\emptyset ,156]^{(1)}\right\} . \end{aligned}$$

We have that

$$\begin{aligned} \begin{array}{ccc} {{\,\mathrm{uh}\,}}(1)= 12456, &{}{{\,\mathrm{uh}\,}}(2)= 1234, &{}{{\,\mathrm{uh}\,}}(3)= 234, \\ {{\,\mathrm{uh}\,}}(4)= 12345, &{}{{\,\mathrm{uh}\,}}(5)= 156, &{}{{\,\mathrm{uh}\,}}(6)= 156, \\ \end{array} \end{aligned}$$

so that the coarsest subdivision ${\hat{S}}$ of ${\mathcal {D}}^{-1}(S)$ has maximal cells

$$\begin{aligned}&\left\{ [\emptyset , 124]^{(2)}, \right. [\emptyset ,234]^{(2)},[\emptyset ,145]^{(2)},[\emptyset ,156]^{(2)}, \\&\quad \left. [1, 12456]^{(2)}, [2,1234]^{(2)},[4,12345]^{(2)},[5,1456]^{(2)} \right\} . \end{aligned}$$

The two cells

$$\begin{aligned}{}[3, {{\,\mathrm{uh}\,}}(3)]^{(2)}&= [3, 234]^{(2)} \subset [\emptyset ,234]^{(2)}, \qquad \text {and}\\ [6, {{\,\mathrm{uh}\,}}(6)]^{(2)}&= [6, 156]^{(2)}\subset [\emptyset ,1456]^{(2)} \end{aligned}$$

are also in ${\hat{S}}$, but they are not maximal: they are edges.

Fig. 7

The subdivision $S\in {\mathcal {B}}^{(1)}(\mathbf {P}_{6})$ of Example 6.12 (left) and ${\hat{S}} \in {\mathcal {B}}^{(2)}(\mathbf {P}_{6})$ (right)

Lemma 6.13

Let $S\in {\mathcal {B}}^{(k+\frac{1}{2})}(\mathbf {P}_{n})$ and let $T\in {\mathcal {B}}^{(k+1)}(\mathbf {P}_{n})$ be such that $S \le {\mathcal {D}}(T)$. Then, the poset ${\mathcal {D}}^{-1}(S) \cap {\mathcal {B}}^{(k+1)}(\mathbf {P}_{n})_{\le T}$ has a unique maximal element.

Proof

Let ${\hat{S}}$ be the maximal element of ${\mathcal {D}}^{-1}(S)$, as described in Corollary 6.11.

Let $T'\in {\mathcal {D}}^{-1}(S)$, which is a refinement of ${\hat{S}}$. If a cell $[X,Y]^{(k+1)}\in T'$ is such that $|X| < k$, then $[X,Y]\in S$ which implies that it is contained in a cell of ${\mathcal {D}}(T)$. Then, $[X,Y]^{(k+1)}$ is contained in a cell of T. Thus, for $T'$ to be a refinement of T, it is enough that $[X,Y]^{(k+1)}\in T'$ is contained in a cell of T for every $[X,Y]\in T'$ with $|X|=k$.

For every such X, the cells $[X,Y']^{(k+1)}\in T$ are a subdivision of the polygon $[X,{{\,\mathrm{uh}\,}}_{{\mathcal {D}}(T)}(X)]^{(k+1)}$. Let $[X,Y_1]^{(k+1)},\dots , [X,Y_l]^{(k+1)}$ be such subdivision. For each Y there are two possibilities:

• If $Y\subseteq {{\,\mathrm{uh}\,}}_{{\mathcal {D}}(T)}(X)$, then $[X,Y]^{(k+1)}$ is contained in a cell of T if and only if there is some $i\in [l]$ such that $Y \subseteq Y_i$.

• If $Y\not \subseteq {{\,\mathrm{uh}\,}}_{{\mathcal {D}}(T)}(X)$, then $[X,Y]^{(k+1)}$ is contained in a cell of T if and only if $[X,Y]^{(k+1)}$ does not intersect the interior of $[X,{{\,\mathrm{uh}\,}}_{{\mathcal {D}}(T)}(X)]^{(k+1)}$. To see this, notice that if $[X,Y]^{(k+1)}$ does not intersect the interior of $[X,{{\,\mathrm{uh}\,}}_{{\mathcal {D}}(T)}(X)]^{(k+1)}$, then all vertices of $[X,Y]^{(k+1)}$ correspond to edges of $S^{(k)}$ contained in the same cell of ${\mathcal {D}}(T)$. If this cell is $[X',Y']$, then $[X',Y']^{(k+1)}\in T$ contains [X, Y].

The discussion above implies that: a $T'\in {\mathcal {D}}^{-1}(S)$ is a refinement of T if and only if all edges of T are also edges in $T'$. This follows from the fact that the only edges in $T'$ not in ${\hat{S}}$ are of the form [X, Y] with $|X|=k$ and $Y\subseteq {{\,\mathrm{uh}\,}}_S(X)$. For each X, there is a unique coarsest subdivision of the polygon $[X,{{\,\mathrm{uh}\,}}_S(X)]^{(k+1)}$ that uses those edges. The subdivision that does that for each X is the unique coarsest refinement of T in ${\mathcal {D}}^{-1}(S)$. $\square$

Example 6.14

Consider the subdivisions T from Example 6.5 and S from Example 6.12. We have that S refines ${\mathcal {D}}(T)$. The unique maximal, (actually, the only) subdivision in ${\mathcal {D}}^{-1}(S) \cap {\mathcal {B}}^{(k+1)}(\mathbf {P}_{n})_{\le T}$ is $T'$ as depicted in Fig. 8.

Fig. 8

The only subdivision $T'$ in ${\mathcal {D}}^{-1}(S) \cap {\mathcal {B}}^{(k+1)}(\mathbf {P}_{6})_{\le T}$

Remark 6.15

One could expect the unique maximal element of Lemma 6.13 to coincide with the maximal element $\widehat{{\mathcal {D}}(T)}$ in ${\mathcal {D}}^{-1}({\mathcal {D}}(T))$. But this is not the case in Example 6.14. In fact, in that example $\widehat{{\mathcal {D}}(T)}$ (whose picture would be as the picture of T in Fig. 6 without the edge $\{45,24\}$) does not refine ${\hat{S}}$.

Corollary 6.16

The maps ${\mathcal {D}}: {\mathcal {B}}^{(k+1)}(\mathbf {P}_{n}) \rightarrow {\mathcal {B}}^{(k+\frac{1}{2})}(\mathbf {P}_{n})$ and ${\mathcal {U}}: {\mathcal {B}}^{(k)}(\mathbf {P}_{n}) \rightarrow {\mathcal {B}}^{(k+\frac{1}{2})}(\mathbf {P}_{n})$ are homotopy equivalences.

Proof

For ${\mathcal {D}}$, conditions (1) and (2) in Babson’s Lemma follow from Corollary 6.11 and Lemma 6.13, respectively, since a poset with a unique maximal element is clearly contractible. For ${\mathcal {U}}$ the proof is completely symmetric. $\square$

Theorem 6.17

The inclusion ${\mathcal {B}}_{{{\,\mathrm{coh}\,}}}^{(k)}(\mathbf {P}_{n}) \rightarrow {\mathcal {B}}^{(k)}(\mathbf {P}_{n})$ is a homotopy equivalence, for $k=1,\dots , n-1$.

Proof

The proof is by induction on k. The base case, $k=1$, is the main result of Rambau and Santos in [19]. Now let us suppose that ${\mathcal {B}}_{{{\,\mathrm{coh}\,}}}^{(k)}(\mathbf {P}_{n}) \rightarrow {\mathcal {B}}^{(k)}(\mathbf {P}_{n})$ is a homotopy equivalence and consider the following diagram, which commutes by Proposition 6.2:

The maps $i^{(k)}$ and $i^{(k+1)}$ are the inclusions of coherent subdivisions into all subdivisions. The maps $r^{(k)}$ and $r^{(k+1)}$ are the restriction of each zonotopal tiling to its k and $k+1$ levels; that is, $S\mapsto S^{(k)}$ and $S\mapsto S^{(k+1)}$ respectively. They are homotopy equivalences since they can be geometrically realized as the identity maps among the normal fans of ${\mathcal {F}}^Z(\mathbf {P}_{n})$, ${\mathcal {F}}^{(k)}(\mathbf {P}_{n})$ and ${\mathcal {F}}^{(k+1)}(\mathbf {P}_{n})$. ${\mathcal {D}}$ and ${\mathcal {U}}$ are homotopy equivalences by Corollary 6.16, and $i^{(k)}$ is a homotopy equivalence by inductive hypothesis, the dotted arrow $i^{(k+1)}$ must also be a homotopy equivalence. $\square$

Corollary 6.18

The restriction map $r^{(k)}: {\mathcal {B}}^Z(\mathbf {P}_{n}) \rightarrow {\mathcal {B}}^{(k)}(\mathbf {P}_{n})$ is a homotopy equivalence, for $k=1,\dots ,n-1$.

Proof

We now use the following commutative diagram:

The top arrow is a homotopy equivalence by [23] and the bottom arrow by Theorem 6.17. The left arrow is also a homotopy equivalence, as mentioned in the proof of Theorem 6.17, so the right arrow is a homotopy equivalence too. $\square$