Abstract
Let \(G\) be a compact Lie group, \(H\) a closed subgroup of maximal rank and \(X\) a topological \(G\)-space. We obtain a variety of results concerning the structure of the \(H\)-equivariant K-ring \(K_H^*(X)\) viewed as a module over the \(G\)-equivariant K-ring \(K_G^*(X)\). One result is that the module has a nonsingular bilinear pairing; another is that the module contains multiplets which are analogous to the Gross–Kostant–Ramond–Sternberg multiplets of representation theory.
Similar content being viewed by others
Abbreviations
- \(\bar{1}\) :
-
Identity coset \(1H\in M\)
- \(A\times _CB\) :
-
Fibred product
- \(\alpha \) :
-
Root of \(G\)
- \(\mathcal B _G\) :
-
Basis of \(\mathcal R _G\)
- BM :
-
Unit ball bundle of cotangent bundle \(T^*M\)
- \(\mathbf{C}_\chi \) :
-
One-dimensional \(G\)-module defined by character \(\chi \in \mathcal{X }(G)\)
- \(\mathbf{Cl}(E)\) :
-
Clifford algebra of a vector space or vector bundle \(E\)
- \([D]\) :
-
Symbol class of operator \(D\)
- \(\mathbf{d}_G\) :
-
Weyl denominator of \(G\)
-
 :
: -
Twisted \(\mathbf{Spin}^c\) Dirac operator
-
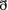 :
: -
\(\mathbf{Spin}^c\) Dirac operator
- \(e^\chi \) :
-
Class of \(\mathbf{C}_\chi \) in \(R(G)\)
- \(\mathbf{e}(D)\) :
-
Euler class of operator \(D\)
- \(\varepsilon _0\) :
-
Standard generator of \(\mathcal{X }(\mathbf{U}(1))\cong \mathbf{Z}\)
- \(\eta \) :
-
Tangent representation \(H\rightarrow \mathbf{GL}(\mathfrak{m })\)
- \(G\) :
-
Compact connected Lie group
- \(G\times ^HV\) :
-
Homogeneous vector bundle
- \(G^{(\sigma )}\) :
-
Central extension of \(G\) by \(\mathbf{U}(1)\)
- \(\Gamma \) :
-
Smooth global sections functor
- \(\gamma \) :
-
c-spinorial character of \(H\)
- \(\mathfrak{g }\) :
-
Lie algebra of \(G\)
- \(\mathfrak{g }_\mathbf{C}^\alpha \) :
-
Root space of \(\mathfrak{g }_\mathbf{C}\)
- \(H\) :
-
Closed subgroup of \(G\), from Sect. 2.5 onward connected and containing \(T\)
- \(H^{(\tau )}\) :
-
Central extension of \(H\) by \(\mathbf{U}(1)\)
- \(i\) :
-
Inclusion \(H\rightarrow G\)
- \(i_!\) :
-
Formal induction
- \(i_*\) :
-
Twisted \(\mathbf{Spin}^c\)-induction
-
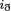 :
: -
\(\mathbf{Spin}^c\)-induction
- \(i_D\) :
-
Induction defined by operator \(D\)
- \({\text{ ind}}_H^G\) :
-
Formal induction
- \(j_G\) :
-
Inclusion \(T\rightarrow G\)
- \(j_H\) :
-
Inclusion \(T\rightarrow H\)
- \(J_G\) :
-
Anti-symmetrizer of \(W_G\)
- \(J_M\) :
-
Relative anti-symmetrizer
- \(J_M^\mathrm{op }\) :
-
“Opposite” of \(J_M\)
- \(K(\mathfrak E )\) :
-
Grothendieck group of category \(\mathfrak E \)
- \(M\) :
-
Homogeneous space \(G{/}H\)
- \(\mathfrak{m }\) :
-
Tangent space \(T_{\bar{1}}M\)
- \(\mathfrak{m }^\alpha \) :
-
Weight space
- \(\omega _M\) :
-
Orientation system of \(M\)
- \(\pi \) :
-
Projection \(T^*M\rightarrow M\)
- \(R(G)\) :
-
Representation ring
- \(R(G)^*\) :
-
Dual \(\mathbf{Z}\)-module of \(R(G)\)
- \(R(G,\sigma )\) :
-
Twisted representation module
- \(R(H)^\vee \) :
-
Dual \(R(G)\)-module of \(R(H)\)
- \(\mathcal R _G\) :
-
Root system of \(G\)
- \(\mathcal R _G^+\) :
-
Positive roots of \(G\)
- \(\mathcal R _M\) :
-
Weights \(\mathcal R _G{\setminus }\mathcal R _H\) of \(\mathfrak{m }_\mathbf{C}\)
- \(\mathcal R _M^+\) :
-
Positive weights \(\mathcal R _G^+{\setminus }\mathcal R _H^+\) of \(\mathfrak{m }_\mathbf{C}\)
- \(\rho _G\) :
-
Half-sum of positive roots of \(G\)
- \(\rho _M\) :
-
Half-character \(\rho _G-\rho _H\)
- \(S\) :
-
Spinor module \(S^0\oplus S^1\) of \(\mathbf{Cl}(\mathfrak{m })\)
- \(\sigma \) :
-
Central extension of \(G\) by \(\mathbf{U}(1)\)
- SM :
-
Unit sphere bundle of cotangent bundle \(T^*M\)
- \(\mathfrak Spin _G^c(M)\) :
-
Set of equivalence classes of invariant \(\mathbf{Spin}^c\)-structures on \(M\)
- \(T\) :
-
Maximal torus of \(G\)
- \(\tau \) :
-
Central extension of \(H\) by \(\mathbf{U}(1)\)
- \(\mathbf{U}(1)\) :
-
Unit circle
- \(W_G\) :
-
Weyl group of \(G\)
- \(W^H\) :
-
Shortest representatives for \(W_G{/}W_H\)
- \(X\) :
-
Topological \(G\)-space
- \(\mathcal{X }(G)\) :
-
Character group \({\text{ Hom}}(G,\mathbf{U}(1))\)
- \(\mathcal{X }(H)^c\) :
-
c-spinorial characters of \(H\)
- \(\zeta \) :
-
Zero section \(M\rightarrow T^*M\)
References
Atiyah, M.: Bott periodicity and the index of elliptic operators. Quart. J. Math. Oxf. Ser. 19(2), 113–140 (1968)
Atiyah, M.: Elliptic operators and compact groups. In: Lecture Notes in Mathematics, vol. 401, Springer, Berlin (1974)
Atiyah, M., Bott, R.: A Lefschetz fixed point formula for elliptic complexes. I. Ann. Math. 86(2), 374–407 (1967)
Atiyah, M., Bott, R.: A Lefschetz fixed point formula for elliptic complexes. II. Applications. Ann. Math. 88(2), 451–491 (1968)
Atiyah, M., Segal, G.: Twisted K-theory. Ukr. Mat. Visn. 1(3), 287–330 (2004)
Atiyah, M., Singer, I.: The index of elliptic operators IV. Ann. Math. (2) 93, 119–138 (1971)
Bott, R.: The index theorem for homogeneous differential operators. In: Differential and Combinatorial Topology, A Symposium in Honor of Marston Morse (Princeton, NJ) (Cairns, S., ed.), Princeton Mathematical Series, vol. 27, Princeton University Press, Princeton, pp. 167–186 (1965)
Bourbaki, N.: Groupes et Algèbres de Lie, Éléments de Mathématique. Diffusion CCLS, Paris (1971)
Bouwknegt, P., Carey, A., Mathai, V., Murray, M., Stevenson, D.: Twisted K-theory and K-theory of bundle gerbes. Comm. Math. Phys. 228(1), 17–45 (2002)
Carey, A., Wang, B.-L.: Thom isomorphism and push-forward map in twisted K-theory. J. K-Theory 1(2), 357–393 (2008)
Donovan, P., Karoubi, M.: Graded Brauer groups and K-theory with local coefficients. Inst. Hautes Études Sci. Publ. Math. 38, 5–25 (1970)
Frobenius, F.G.: Gesammelte Abhandlungen, Herausgegeben von J.-P. Serre. Springer, Berlin (1968)
Gross, B., Kostant, B., Ramond, P., Sternberg, S.: The Weyl character formula, the half-spin representations, and equal rank subgroups. Proc. Natl. Acad. Sci. USA 95(15), 8441–8442 (1998)
Guillemin, V., Ginzburg, V., Karshon, Y.: Moment maps, cobordisms, and Hamiltonian group actions, Mathematical Surveys and Monographs, vol. 98. American Mathematical Society, Providence (2002) [Appendix J by M. Braverman (2002)]
Harada, M., Landweber, G., Sjamaar, R.: Divided differences and the Weyl character formula in equivariant K-theory. Math. Res. Lett. 17(3), 507–527 (2010)
Hirzebruch, F., Slodowy, P.: Elliptic genera, involutions, and homogeneous spin manifolds. Geom. Dedicata 35(1–3), 309–343 (1990)
Hodgkin, L.: The equivariant Künneth theorem in K-theory. In: Topics in K-theory, Lecture Notes in Mathematics, vol. 496, pp. 1–101, Springer, Berlin (1975)
Karoubi, M.: K-theory. An Introduction, Grundlehren der Mathematischen Wissenschaften, vol. 226, Springer, Berlin (1978)
Kazhdan, D., Lusztig, G.: Proof of the Deligne-Langlands conjecture for Hecke algebras. Invent. Math. 87(1), 153–215 (1987)
Kostant, B.: A cubic Dirac operator and the emergence of Euler number multiplets of representations for equal rank subgroups. Duke Math. J. 100(3), 447–501 (1999)
Krepski, D.: Pre-quantization of the moduli space of flat \(G\)-bundles over a surface. J. Geom. Phys. 58(11), 1624–1637 (2008)
Lam, T.Y.: Lectures on Modules and Rings, Graduate Texts in Mathematics, vol. 189. Springer, New York (1999)
Lam, T.Y.: Serre’s Problem on Projective Modules. Springer Monographs in Mathematics. Springer, Berlin (2006)
Landweber, G.: Twisted representation rings and Dirac induction. J. Pure Appl. Algebra 206(1–2), 21–54 (2006)
Landweber, G., Sjamaar, R.: Homogeneous \({ Spin}^c\)-structures, in preparation
Mathai, V., Melrose, R., Singer, I.: Equivariant and fractional index of projective elliptic operators. J. Differ. Geom. 78(3), 465–473 (2008)
McLeod, J.: The Künneth formula in equivariant K-theory. In: Algebraic Topology (Waterloo, 1978) (Hoffman, P., Snaith, V., eds.), Lecture Notes in Mathematics, vol. 741, Springer, Berlin, pp. 316–333 (1979)
Meinrenken, E.: On the quantization of conjugacy classes. Enseign. Math. 55(1–2), 33–75 (2009)
Murray, M., Singer, M.: Gerbes, Clifford modules and the index theorem. Ann. Glob. Anal. Geom. 26(4), 355–367 (2004)
Pittie, H.: Homogeneous vector bundles on homogeneous spaces. Topology 11, 199–203 (1972)
Quillen, D.: Higher algebraic K-theory I. In: Algebraic K-Theory I: Higher K-Theories (Seattle, WA, 1972) (Bass, H., ed.), Lecture Notes in Mathematics, vol. 341. Springer, Berlin, pp. 85–147 (1973)
Quillen, D.: Projective modules over polynomial rings. Invent. Math. 36, 167–171 (1976)
Rosenberg, J., Schochet, C.: The Künneth theorem and the universal coefficient theorem for equivariant K-theory and KK-theory. Mem. Amer. Math. Soc. 62(348), vi+95 (1986)
Segal, G.: Equivariant K-theory. Inst. Hautes Études Sci. Publ. Math. 34, 129–151 (1968)
Segal, G.: The representation ring of a compact Lie group. Inst. Hautes Études Sci. Publ. Math. 34, 113–128 (1968)
Shapiro, A.: Group extensions of compact Lie groups. Ann. Math. 50(2), 581–586 (1949)
Shapiro, J.: A duality theorem for the representation ring of a compact connected Lie group. Ill. J. Math. 18, 79–106 (1974)
Shapiro, J.: On the algebraic structure of the K-theory of \(G_2/SU(3)\) and \(F_4/Spin(9)\). Ill. J. Math. 18, 509–515 (1974)
Slebarski, S.: The Dirac operator on homogeneous spaces and representations of reductive Lie groups I. Am. J. Math. 109(2), 283–301 (1987)
Slebarski, S.: The Dirac operator on homogeneous spaces and representations of reductive Lie groups II. Am. J. Math. 109(3), 499–520 (1987)
Slebarski, S.: The Dirac operator on homogeneous spaces and representations of reductive Lie groups III. Am. J. Math. 110(3), 451–471 (1988)
Snaith, V.: On the Künneth formula spectral sequence in equivariant K-theory. Proc. Camb. Philos. Soc. 72, 167–177 (1972)
Steinberg, R.: On a theorem of Pittie. Topology 14, 173–177 (1975)
Suslin, A.: Projective modules over polynomial rings are free. Dokl. Akad. Nauk SSSR 229(5), 1063–1066 (1976) [(Russian), English translation in Soviet Math. Dokl. 17(4), 1160–1164 (1976)]
Tu, J.-L., Xu, P., Laurent-Gengoux, C.: Twisted K-theory of differentiable stacks. Ann. Sci. École Norm. Sup. (4) 37(6), 841–910 (2004)
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix: twisted K-theory
In this appendix we summarize the necessary facts from twisted K-theory in a form suited to our purpose. Like the original treatment by Donovan and Karoubi [11], we cover only K-theory twisted by torsion classes. We denote by \(X\) a compact topological space and by \(G\) and \(H\) two (not necessarily connected) compact Lie groups. Contrary to our convention elsewhere in the paper, we do not assume \(H\) to be a subgroup of \(G\).
1.1 Twists and twisted vector bundles
A twist of \(X\) is a pair \(\tau =(P,H^{(\tau )})\), where \({\text{ pr}}:P\rightarrow X\) is a principal \(H\)-bundle over \(X\) and \(H^{(\tau )}\) is a central extension of \(H\) by \(\mathbf{U}(1)\). We regard \(P\) as an \(H^{(\tau )}\)-space on which the central circle \(\mathbf{U}(1)\) acts trivially. A \(\tau \) -twisted vector bundle over \(X\) is an \(H^{(\tau )}\)-equivariant complex vector bundle over \(P\) which is of level \(1\), in the sense that the central circle of \(H^{(\tau )}\) acts on \(E\) by scalar multiplication on the fibres.
A morphism between \(\tau \)-twisted vector bundles \(E_1\) and \(E_2\) is an \(H^{(\tau )}\)-equivariant vector bundle homomorphism \(E_1\rightarrow E_2\). We denote by \(\mathfrak Vec (X,\tau )\) the category of \(\tau \)-twisted vector bundles. This is an additive category, in which there is an obvious notion of an exact sequence. Thus, we can form the Grothendieck group of \(\mathfrak Vec (X,\tau )\), which we will denote by \(K(X,\tau )\).
A twist \(\tau \) is a simple example of a gerbe with band \(\mathbf{U}(1)\) over \(X\), and \(K(X,\tau )\) is called the \(\tau \) -twisted K-group of \(X\), or the K-group of \(X\) with coefficients in \(\tau \). See [9, § 2] or [45, § 2.5] for more general notions of a gerbe and a comparison with other versions of twisted K-theory.
We can multiply a twisted bundle \(F\) by an ordinary vector bundle \(E\) on \(X\) by the rule \(E\cdot F={\text{ pr}}^*E\otimes F\). This rule turns \(K(X,\tau )\) into a \(K(X)\)-module. More generally, let \(\tau _1=(P_1,H_1^{(\tau _1)})\) and \(\tau _2=(P_2,H_2^{(\tau _2)})\) be two twists of \(X\). The sum of \(\tau _1\) and \(\tau _2\) is the twist \(\tau =(P,H^{(\tau )})\), where \(P\) is the fibred product \(P_1\times _XP_2\), viewed as a principal bundle over \(X\) with structure group \(H=H_1\times H_2\), and the central extension \(H^{(\tau )}\) is the quotient of \(H_1^{(\tau _1)}\times H_2^{(\tau _2)}\) by the anti-diagonal copy of \(\mathbf{U}(1)\). Any \(\tau _1\)- and \(\tau _2\)-twisted bundles on \(X\) can be lifted to \(P\) and the tensor product of the lifts is a \(\tau _1+\tau _2\)-twisted bundle. This defines a multiplication law
A twist \(\tau \) pulls back under a continuous map \(f:Y\rightarrow X\) in an evident way, and we have an induced homomorphism
The twist \(\tau \) is (Morita) trivial if there exists a trivialization, that is, a principal \(H^{(\tau )}\)-bundle \(Q\) over \(X\) such that \(P\) is the quotient of \(Q\) by the central circle of \(H^{(\tau )}\). (If the extension \(H^{(\tau )}\) of \(H\) is trivial, then the twist \(\tau \) is Morita trivial, but the converse is false.) If \(\tau \) is Morita trivial, then
This isomorphism depends on the choice of the trivialization \(Q\).
Example 6.1.1
Let \(V\) be an oriented real vector bundle of rank \(m\) over \(X\) provided with a Riemannian metric. The orientation twist or orientation system associated with \(V\) is the pair \(\omega _V=(\mathbf{SO}(V),\mathbf{Spin}^c(m))\). Here \(\mathbf{SO}(V)\) is the oriented orthogonal frame bundle of \(V\), which has structure group \(\mathbf{SO}(m)\), and \(\mathbf{Spin}^c(m)\) is the \(\mathbf{Spin}^c\)-group of the Euclidean space \(\mathbf{R}^m\). The orientation system is Morita trivial precisely when \(V\) possesses a \(\mathbf{Spin}^c\)-structure, tht is, an orientation in K-theory. If \(X\) is an oriented Riemannian manifold, the orientation twist \(\omega _X\) of \(X\) is defined to be the orientation twist of the tangent bundle of \(X\).
Example 6.1.2
Let \(\tau \) be a central extension of a compact Lie group \(H\) by \(\mathbf{U}(1)\). By letting \(H\) act on itself by right multiplication we can view \(H\) as a principal bundle over the one-point space \(X=\mathrm{pt}\). From this point of view \(\tau \) is nothing but a twist of a point. As such it is Morita trivial, and therefore it follows from (6.1) that \(K(\mathrm{pt},\tau )\cong \mathbf{Z}\).
Suppose the compact Lie group \(G\) acts continuously on \(X\). A twist \(\tau =(P,H^{(\tau )})\) of \(X\) is \(G\) -equivariant if the principal bundle \(P\) is \(G\)-equivariant, that is, equipped with a \(G\)-action by bundle maps which lifts the \(G\)-action on the base \(X\) and which commutes with the action of the structure group \(H\). A \(G\) -equivariant \(\tau \) -twisted vector bundle over \(X\) is a \(G\times H^{(\tau )}\)-equivariant complex vector bundle over \(P\) which is of level \(1\) with respect to \(H^{(\tau )}\). Such twisted bundles are the objects of an exact category \(\mathfrak Vec _G(X,\tau )\), whose K-group \(K_G(X,\tau )\) is the equivariant K-group of \(X\) with coefficients in \(\tau \).
Example 6.1.3
The orientation twist of an oriented Riemannian vector bundle \(V\) is equivariant with respect to any compact Lie group which acts on \(V\) by orientation-preserving isometric bundle maps. In particular, the orientation twist of an oriented Riemannian manifold \(X\) is equivariant with respect to any compact Lie group which acts on \(X\) by orientation-preserving isometries.
Example 6.1.4
Let \(X=\mathrm{pt}\) and let \(\tau \) be as in Example 6.1.2. We turn \(\tau \) into an \(H\)-equivariant twist by letting \(H\) act on \(H\) by left multiplication. Every \(H\times H^{(\tau )}\)-equivariant vector bundle \(E\) over \(H\) trivializes equivariantly to a product bundle \(E\cong H\times U\). On this product bundle \(H\) acts on the base \(H\) by left multiplication and trivially on the vector space \(U\), and \(H^{(\tau )}\) acts on the base by right multiplication and linearly on the fibre. Thus, the bundle \(E\) is of level \(1\) if and only if the \(H^{(\tau )}\)-module \(U\) is of level \(1\). It follows that the category \(\mathfrak Vec _H(\mathrm{pt},\tau )\) is equivalent to the category of level \(1\) \(H^{(\tau )}\)-modules. We conclude that \(K_H(\mathrm{pt},\tau )\cong R(H,\tau )\), the twisted representation module of \(H\).
Example 6.1.5
Generalizing Example 6.1.4, we let \(X\) be a topological \(H\)-space and \(p:X\rightarrow \mathrm{pt}\) the constant map. The \(H\)-equivariant twist \(\tau \) pulls back to the \(H\)-equivariant twist \(p^*\tau \) on \(X\). We view \(X\) as an \(H^{(\tau )}\)-space on which the central circle acts trivially. As in Example 6.1.4 one shows that the category \(\mathfrak Vec (X,p^*\tau )\) is equivalent to the category of \(H^{(\tau )}\)-equivariant level \(1\) vector bundles on \(X\). Thus \(K_H(X,p^*\tau )\) is the Grothendieck group of \(H^{(\tau )}\)-equivariant level \(1\) vector bundles on \(X\). To simplify the notation we will often write this group as \(K_H(X,\tau )\).
Example 6.1.6
(induced twists) Continuing Example 6.1.5, we suppose that \(H\) is a subgroup of \(G\) and let \(i:H\rightarrow G\) the inclusion map. We view the product \(G\times X\) as a \(G\)-equivariant principal \(H\)-bundle over the associated bundle \(G\times ^HX\). Hence the pair
is a \(G\)-equivariant twist of \(G\times ^HX\), called the twist induced by \(\tau \). If \(E\) is a \(\tau \)-twisted vector bundle over \(X\), then \(G\times E\) is a \(i_*\tau \)-twisted vector bundle over \(G\times ^HX\). The map \(E\mapsto G\times E\) defines an equivalence of categories between \(\mathfrak Vec (X,\tau )\) and \(\mathfrak Vec (G\times ^HX,i_*\tau )\). Thus we have a natural isomorphism
For \(X=\mathrm{pt}\) this specializes to \(K_G(M,i_*\tau )\cong R(H,\tau )\), where \(M=G{/}H\). For simplicity we will often write \(K_G(G\times ^HX,\tau )\) instead of \(K_G(G\times ^HX,i_*\tau )\).
1.2 Relative twisted K-theory
Relative twisted K-classes are presented by complexes of twisted vector bundles. Let \(X\) be a compact \(G\)-space and let \(\tau =(P,H^{(\tau )})\) be a \(G\)-equivariant twist of \(X\). Consider the category \(\mathfrak Vec _G^*(X,\tau )\) of bounded complexes associated with the additive category \(\mathfrak Vec _G(X,\tau )\). Thus an object of \(\mathfrak Vec _G^*(X,\tau )\) is a \(\mathbf{Z}\)-graded \(G\)-equivariant \(\tau \)-twisted bundle \(E^*\) such that \(E^j=0\) for almost all \(j\), furnished with a differential of degree \(1\). Let \(Y\) be a closed \(G\)-invariant subspace of \(X\). We denote by \(\mathfrak Vec _G^*(X,Y,\tau )\) the full subcategory of \(\mathfrak Vec _G^*(X,\tau )\) comprising all objects \(E^*\) with the property that the restriction of \(E^*\) to the subspace \({\text{ pr}}^{-1}(Y)\) of \(P\) is an exact complex. The set \(L_G(X,Y,\tau )\) of isomorphism classes of \(\mathfrak Vec _G^*(X,Y,\tau )\) is an abelian monoid. A quotient of \(L_G(X,Y,\tau )\) by an appropriate submonoid (which is defined in the same way as in ordinary K-theory; see [34, § 3]) is the relative twisted K-group \(K_G(X,Y,\tau )\) of \(X\). The Euler characteristic map \(L_G(X,Y,\tau )\rightarrow K_G(X,\tau )\) defined by \([E^*]\mapsto \sum _j(-1)^j[E^j]\) induces a homomorphism
which is an isomorphism if \(Y\) is empty.
The group \(K_G^0(X,Y,\tau )=K_G(X,Y,\tau )\) is the degree \(0\) part of the \(\mathbf{Z}{/}2\mathbf{Z}\)-graded K-group \(K_G^*(X,Y,\tau )\). The degree \(1\) part is defined by
1.3 The Thom isomorphism
Let \(X\) be a compact \(G\)-space, and let \(\tau \) be a \(G\)-equivariant twist of \(X\). Let \(\pi :V\rightarrow X\) be a \(G\)-equivariant oriented real vector bundle of even rank \(m=2l\) equipped with an invariant Riemannian metric, and let \(\omega _V\) be the orientation twist of \(V\). We denote the unit ball bundle of \(V\) by BV, the unit sphere bundle by SV and the zero section by \(\zeta :X\rightarrow V\). Let \(P=\mathbf{SO}(V)\). The spinor module \(S=S^0\oplus S^1\) of the Clifford algebra \(\mathbf{Cl}(\mathbf{R}^{2l})\) is a level \(1\) \(\mathbf{Spin}^c(2l)\)-module, so the product bundle \(E=\pi ^*(P)\times S\) is a \(\mathbf{Z}{/}2\mathbf{Z}\)-graded \(\pi ^*(\omega _V)\)-twisted vector bundle over (the total space of) \(V\). Consider the two-term \(G\times \mathbf{Spin}^c(2l)\)-equivariant complex of vector bundles
defined by placing the term \(E^j\) in degree \(j\) and for each \(v\in V\) letting \(\text{ cliff}(v):E_v^0\rightarrow E_v^1\) be Clifford multiplication by \(v\). Since \(\text{ cliff}(v)\) is an isomorphism for \(v\ne 0\), the complex (6.2) defines a class in \(L_G(BV,SV,\pi ^*\omega _V)\), and hence a class
which is called the Thom class of \(V\). The Thom map is the map
defined by \(\zeta _*(a)=\pi ^*(a)\mathbf{th}(V)\). The following result is [18, Theorem IV.6.21]. See also [10, § 3.2] for a discussion closer to our treatment.
Theorem 6.3.1
The Thom map is an isomorphism of graded \(K_G^*(X)\)-modules.
Appendix: Central extensions
In this appendix we gather a few elementary facts regarding central extensions. The notation is as stated at the beginning of Sect. 2. In particular \(G\) denotes a compact connected Lie group. In addition \(\check{G}\) denotes a connected central extension of \(G\) by a compact abelian Lie group \(C\),
A complex \(\check{G}\)-module \(V\) has central character \(\chi \in \mathcal{X }(C)\) if the subgroup \(C\) acts on \(V\) by \(c\cdot v=\chi (c)v\). Let \(\mathfrak Rep ^\chi (\check{G})\) be the category of finite-dimensional complex \(\check{G}\)-modules of central character \(\chi \). We call the Grothendieck group \(R^\chi (\check{G})\) of \(\mathfrak Rep ^\chi (\check{G})\) the \(\chi \) -twisted representation module of \(G\). The category \(\mathfrak Rep ^0(\check{G})\) (where \(\chi =0\) is the trivial character) is equivalent to \(\mathfrak Rep (G)\), so the groups \(R^0(\check{G})\) and \(R(G)\) are isomorphic. The tensor product functor
induces a bi-additive map
In particular \(R^\chi (\check{G})\) is an \(R(G)\)-module for all \(\chi \).
Lemma 7.1
-
(i)
The \(R(G)\)-module \(R(\check{G})\) is the direct sum of the submodules \(R^\chi (\check{G})\) over all \(\chi \in \mathcal{X }(C)\). Each summand \(R^\chi (\check{G})\) is nonzero.
-
(ii)
Let \(\check{T}\subset \check{G}\) be the inverse image of \(T\). Then \(\check{T}\) is a maximal torus of \(\check{G}\); for each character \(\chi \) of \(C\) the submodule \(R^\chi (\check{T})\) of \(R(\check{T})\) is preserved by the \(W_G\)-action; and the restriction homomorphism \(R^\chi (\check{G})\rightarrow R^\chi (\check{T})\) is an isomorphism onto \(R^\chi (\check{T})^{W_G}\).
Proof
Every \(\check{G}\)-module \(V\) decomposes under the action of \(C\) into a direct sum \(\bigoplus _{\chi \in \mathcal{X }(C)}V^\chi \) of isotypical submodules \(V^\chi \). This decomposition is functorial and defines an equivalence of categories
Passing to Grothendieck groups we obtain the direct sum decomposition in (i). Each of the submodules \(R^\chi (\check{G})\) is nonzero, because there exists an irreducible representation of \(\check{G}\) with central character \(\chi \), for instance an appropriate subrepresentation of the formally induced representation \({\text{ ind}}_C^{\check{G}}(\mathbf{C}_\chi )\). Since \(C\) is central in \(\check{G}\), the group \(\check{T}\) is a maximal torus of \(\check{G}\), and the homomorphism \(\check{G}\rightarrow G\) induces isomorphisms of root systems \(\mathcal R _{\check{G}}\cong \mathcal R _G\) and of Weyl groups \(W_{\check{G}}\cong W_G\). The homomorphism \(\check{T}\rightarrow T\) is \(W_G\)-equivariant. The \(W_G\)-action on \(\check{T}\) fixes \(C\) and therefore the submodule \(R^\chi (\check{T})\) of \(R(\check{T})\) is \(W_G\)-stable for each \(\chi \in \mathcal{X }(C)\). The isomorphism \(R^\chi (\check{G})\cong R^\chi (\check{T})^{W_G}\) now follows from \(R(\check{G})\cong R(\check{T})^{W_G}\). \(\square \)
Let \(V\) be an irreducible \(\check{G}\)-module. By Schur’s lemma, the central subgroup \(C\) acts on \(V\) by a character \(\chi _V\). Define
for \(c\in C\). By linear extension, this formula defines a \(C\)-action on the complexified representation ring \(R(\check{G})_\mathbf{C}\) by ring automorphisms. The ring of \(C\)-invariants is
Recall that the rank of a module \(A\) over a domain \(R\) is the dimension of the vector space \(F\otimes _RA\), where \(F\) is the fraction field of \(R\), and is denoted by \({\text{ rank}}_R(A)\).
Lemma 7.2
\({\text{ rank}}_{R(G)}(R^\chi (\check{G}))=1\) for every \(\chi \in \mathcal{X }(C)\).
Proof
Assume first that \(C\) is finite. Since \(G\) and \(\check{G}\) are connected, the rings \(R(G)\) and \(R(\check{G})\) have no zero divisors, so we can form the fraction fields \(\mathbf{K}\) of \(R(G)_\mathbf{C}\) and \(\check{\mathbf{K}}=R(\check{G})_\mathbf{C}\otimes _{R(G)_\mathbf{C}}\mathbf{K}\) of \(R(\check{G})_\mathbf{C}\). It follows from (7.2) that \(\check{\mathbf{K}}\) is a Galois extension of \(\mathbf{K}\) with Galois group \(C\), which implies \(\dim _\mathbf{K}(\check{\mathbf{K}})=|C|\). For \(\chi \in \mathcal{X }(C)\) let
which is a \(\mathbf{K}\)-linear subspace of \(\check{\mathbf{K}}\). It follows from Lemma 7.1(i) that as a vector space over \(\mathbf{K}\)
where each of the summands is nonzero. The number of summands is \(|C|\) because of the fact that \(\mathcal{X }(C)\cong C\), and therefore \(\dim _\mathbf{K}(\check{\mathbf{K}}^\chi )=1\) for all \(\chi \). Hence
For general \(C\) we make the basic observation, which appears to go back to Shapiro [36], that the compact central extension \(\check{G}\) is the pushout of a finite central extension
One produces \(\tilde{G}\) by choosing a Lie algebra homomorphism \(\kappa :\mathfrak{g }\rightarrow \check{\mathfrak{g }}\) which splits the exact sequence
One can choose \(\kappa \) to be defined over \(\mathbf{Q}\); this ensures that it exponentiates to a Lie group homomorphism \(\kappa :\tilde{G}\rightarrow \check{G}\), where \(\tilde{G}\) is a finite connected covering group of \(G\). Let \(Z\) be the kernel of the covering \(\tilde{G}\rightarrow G\); then \(\kappa (Z)\) is contained in \(C\). Let \(\chi \) be a character of \(C\) and \(\kappa ^*(\chi )\) its pullback to \(Z\). Then the \(R(G)\)-module \(R^\chi (\check{G})\) is isomorphic to \(R^{\kappa ^*(\chi )}(\tilde{G})\), and we already know that the latter is of rank \(1\). \(\square \)
Example 7.3
Let \(\check{G}_1=\check{G}_2=\mathbf{SU}(2)\) and
Then \(R(\check{G})\cong R(\check{G}_1)\otimes R(\check{G}_2)\cong \mathbf{Z}[x_1,x_2]\). Identify \(\mathcal{X }(C)\) with \(\mathbf{Z}{/}2\mathbf{Z}=\{0,1\}\); then \(C\) acts on the monomial \(x_1^{r_1}x_2^{r_2}\in R(\check{G})\) with weight \((r_1+r_2)\text{ mod}\,2\). Hence \(R(\check{G})\) is the direct sum of the submodules
where the congruences are modulo \(2\). As a ring,
where the inclusion \(R(G)\rightarrow R(\check{G})\) is given by
The twisted module \(R^1(\check{G})\) is generated by \(x_1\) and \(x_2\), which are subject to the single relation \(y_3x_1-y_1x_2=0\). Over the quotient field of \(R(G)\) the two generators are multiples of each other, \(x_2=(y_2y_3^{-1})x_1\) and \(x_1=(y_1y_3^{-1})x_2\), so \(R^1(\check{G})\) is of rank \(1\), as predicted by Lemma 7.2. However, \(R^1(\check{G})\) is not generated by any single element and is therefore not free.
Appendix: Shifted anti-invariants
This appendix is devoted to the proof of the statement below (Proposition 3.2.5 in the main text). We use the notation defined in Sect. 3. In particular, \(G\) is a compact connected Lie group with maximal torus \(T\), \(\omega _{G{/}T}\) is the orientation system of the flag variety \(G{/}T\) defined in (3.2), \(J_G\) is the anti-symmetrizer (3.5), and \(\mathbf{d}_G\) is the Weyl denominator (3.7). Recall that \(A^{-W_G}\) denotes the set of anti-invariant elements of a \(W_G\)-module \(A\). If \(G\) is semisimple and simply connected, then \(\rho _G\in \mathcal{X }(T)\) and therefore the \(R(T)\)-module \(R(T,\omega _{G{/}T})\) is \(W_G\)-equivariantly isomorphic to \(R(T)\) by Lemma 3.2.1(iii). The proposition is then a standard fact; see e.g. [8, § VI.3, Proposition 2]. We will deduce the general case from this special case.
Proposition.
-
(i)
The \(W_G\)-action on \(R(T^{(\omega _{G{/}T})})\) preserves \(R(T,\omega _{G{/}T})\).
-
(ii)
The set of anti-invariants \(R(T,\omega _{G{/}T})^{-W_G}\) is a free \(R(G)\)-module of rank \(1\) generated by \(\mathbf{d}_G\).
-
(iii)
The elements \(J_G(e^\lambda )\), with \(\lambda \in \rho _G+\mathcal{X }(T)\) strictly dominant, form a basis of the \(\mathbf{Z}\)-module \(R(T,\omega _{G{/}T})^{-W_G}\).
Proof
Put
We identify \(R(T)\) with \(\mathbf{Z}[\mathcal{X }(T)]\) and \(R(T,\omega )\) with \(R(T)\,e^\rho =\mathbf{Z}[\rho +\mathcal{X }(T)]\) as in Remark 3.2.2. The fact that \(\rho -w(\rho )\) is in the root lattice for all \(w\in W\) implies that the \(W\)-action on \(\mathcal{X }(T)_\mathbf{Q}\) preserves the affine lattice \(\rho +\mathcal{X }(T)\). This proves (i). Let \(\phi :\tilde{G}\rightarrow G\) be a compact connected covering group which is the product \(\tilde{G}=C\times \bar{G}\) of a torus \(C\) and a simply connected group \(\bar{G}\). Let \(\tilde{T}\) be the maximal torus \(\phi ^{-1}(T)\) of \(\tilde{G}\) and identify \(\mathcal{X }(T)\) with its image \(\phi ^*(\mathcal{X }(T))\). Let \(\bar{T}\) be the maximal torus \(\bar{G}\cap \tilde{T}\) of \(\bar{G}\). Since \(\bar{G}\) is simply connected, \(\rho \in \mathcal{X }(\bar{T})\) and therefore \(\mathbf{d}\in R(\bar{T})\). We have
because \(W\) acts trivially on \(R(C)\) and \(R(C)\) is a free abelian group. Since \(\bar{G}\) is simply connected, it follows from [8, § VI.3, Proposition 2] that
Therefore
Now let \(a\in R(T,\omega )^{-W}\subset R(\tilde{T})^{-W}\). It follows from (8.1) that \(a=b\mathbf{d}\) for some \(b\in R(\tilde{T})^W\). We need to argue that \(b\in R(T)\). Let \(K\subset \tilde{T}\) be the kernel of the covering homomorphism \(\phi :\tilde{G}\rightarrow G\). This group acts on the complexified representation ring \(R(\tilde{T})_\mathbf{C}\) as in (7.1), and the ring of \(K\)-invariants \((R(\tilde{T})_\mathbf{C})^K\) is isomorphic to \(R(T)_\mathbf{C}\). Since \(a\) and \(\mathbf{d}\) are in \(R(T,\omega )=R(T)e^\rho \), we have \(k\cdot a=\rho (k)a\) and \(k\cdot \mathbf{d}=\rho (k)\mathbf{d}\) for all \(k\in K\) and hence
It follows that \(k\cdot b=b\) for all \(k\in K\), that is, \(b\in R(T)\). This proves (ii). (iii) is proved in exactly the same way as [8, § VI.3, Proposition 1]. \(\square \)
Appendix: Homogeneous \(\mathbf{Spin}^c\)-structures
In this appendix we review the classification of invariant \(\mathbf{Spin}^c\)-structures on equal-rank homogeneous spaces, which is surely well known but for which we could not find a reference. (But see [16, §2.6] and also Example 9.5 below for remarks on the \(\mathbf{Spin}\) case.) See [28, Example 4.6] and [25] for examples of maximal-rank homogeneous spaces that do not carry invariant \(\mathbf{Spin}^c\)-structures.
The notation and the assumptions are as explained at the beginning of Sects. 2 and 3. Recall that \(G\) denotes a compact connected Lie group, \(H\) a closed and connected subgroup of maximal rank and \(T\) a common maximal torus of \(G\) and \(H\). Recall also that \(\mathfrak{m }=T_{\bar{1}}M\) denotes the tangent space at the identity coset of the homogeneous space \(M=G{/}H\), and \(\eta :H\rightarrow \mathbf{SO}(\mathfrak{m })\) denotes the tangent representation. We denote the set of equivalence classes of \(G\)-invariant \(\mathbf{Spin}^c\)-structures on \(M\) by \(\mathfrak Spin _G^c(M)\).
Definition 9.1
The orthogonal representation \(\eta \) is c-spinorial if it lifts to a homomorphism \(H\rightarrow \mathbf{Spin}^c(\mathfrak{m })\). The subgroup \(H\) is c-spinorial if \(\eta \) is c-spinorial.
Note that \(\eta \) is c-spinorial if and only if \(M\) possesses a \(G\)-invariant \(\mathbf{Spin}^c\)-structure, that is, if and only if \(\mathfrak Spin _G^c(M)\) is nonempty. Moreover, liftings of \(\eta \) to \(\mathbf{Spin}^c(\mathfrak{m })\) correspond bijectively to elements of \(\mathfrak Spin _G^c(M)\).
A lifting of \(\eta \) to \(\mathbf{Spin}^c(\mathfrak{m })\) determines a trivialization \(s\) of the central extension

defined in (3.2). Conversely, given a section \(s\) of \(\phi \) we can compose it with the canonical homomorphism \(\hat{\eta }:H^{(\omega )}\rightarrow \mathbf{Spin}^c(\mathfrak{m })\) to obtain a lifting of \(\eta \),
Thus, we have a natural one-to-one correspondence between \(\mathfrak Spin _G^c(M)\) and the set of trivializations of the orientation system \(\omega \).
The determinant character is the character \(\det :H^{(\omega )}\rightarrow \mathbf{U}(1)\) obtained by pulling back the determinant character of \(\mathbf{Spin}^c(\mathfrak{m })\), which is defined by \(\det ([z,a])=z^2\). The homomorphism
is a double covering map. Let \(s\) be a section of \(\phi \), and let \(\gamma \) be the character \(\det \circ s\) of \(H\). Then \(s\) is a lifting homomorphism of \(\gamma \times {\text{ id}}\), as in the commutative diagram

and so \(s=s_\gamma \) is uniquely determined by \(\gamma \).
Definition 9.2
A character \(\gamma \in \mathcal{X }(H)\) is c-spinorial (relative to the orthogonal \(H\)-module \(\mathfrak{m }\)) if the lifting \(s_\gamma \) of \(\gamma \times {\text{ id}}\) exists. We denote the set of \(c\)-spinorial characters by \(\mathcal{X }(H)^c\).
The conclusion is that we have natural bijections between the set \(\mathfrak Spin _G^c(M)\), the set of trivializations of \(\omega \) and the set \(\mathcal{X }(H)^c\). This proves the first part of the following proposition. The map \(\nu :\mathcal{X }(H)\rightarrow \frac{1}{2}\mathcal{X }(T)\) in the second part is defined by
Proposition 9.3
-
(i)
For a \(c\)-spinorial character \(\gamma \), define a \(G\)-invariant principal \(\mathbf{Spin}^c(\mathfrak{m })\)-bundle over \(M\) by
$$\begin{aligned} \mathbf{P}_\gamma =G\times ^H\mathbf{Spin}^c(\mathfrak{m }), \end{aligned}$$where the right-hand side denotes the quotient of \(G\times \mathbf{Spin}^c(\mathfrak{m })\) by the \(H\)-action \(h\cdot (g,k)=(gh^{-1},\hat{\eta }(s_\gamma (h))k)\). The map
$$\begin{aligned} f:\mathcal{X }(H)^c\longrightarrow \mathfrak Spin _G^c(M) \end{aligned}$$which sends \(\gamma \) to the equivalence class of \(\mathbf{P}_\gamma \) is bijective. In particular \(\mathfrak Spin _G^c(M)\) is nonempty if and only if \(\mathcal{X }(H)^c\) is nonempty.
-
(ii)
A character \(\gamma \) of \(H\) is \(c\)-spinorial if and only if \(\nu (\gamma )\in \mathcal{X }(T)\). Hence \(\mathcal{X }(H)^c=\nu ^{-1}(\mathcal{X }(T))\).
Proof
It remains to prove (ii). By covering space theory and our standing assumption that \(H\) is connected, a lifting \(s\) of \(\gamma \times {\text{ id}}\) exists if and only if it exists on the level of fundamental groups, as in the diagram

Let \(\mathcal{Y }(T)={\text{ Hom}}(\mathbf{U}(1),T)\) denote the cocharacter group of \(T\). The fundamental group \(\pi _1(H)\) is naturally isomorphic to \(\mathcal{Y }(T){/}Q(\mathcal R _H^\vee )\), where \(Q(\mathcal R _H^\vee )\) is the coroot lattice in \(\mathcal{Y }(T)\). (See e.g. [8, § IX.4.6].) Since \(\psi \) is a covering map, \(\psi _*\) maps the coroot system of \(H^{(\omega )}\) bijectively to that of \(\mathbf{U}(1)\times H\). Therefore, the lifting problem (9.1) is equivalent to the lifting problem

Since \(\mathcal{X }(T)\) and \(\mathcal{Y }(T)\) are dual abelian groups, this lifting problem is equivalent to the dual extension problem

By Lemma 3.2.1(ii), \(\mathcal{X }(T^{(\omega )})\) is the direct sum of \(\phi ^*(\mathcal{X }(T))\) and \(\mathbf{Z}\cdot (\varepsilon _0-\rho _M)\). Let \(\mathcal{X }\) be the image of \(\psi ^*\), which is a sublattice of \(\mathcal{X }(T^{(\omega )})\) of index \(2\). Since \(2\rho _M\) is in \(\mathcal{X }(T)\) and \(\psi ^*\) maps the generator \(\varepsilon _0\) of \(\mathcal{X }(\mathbf{U}(1))\) to the determinant character \(\det =2\varepsilon _0\), the element \(\varepsilon _0-\rho _M\in \mathcal{X }(T^{(\omega )})\) is a representative of the nontrivial coset in \(\mathcal{X }(T^{(\omega )}){/}\mathcal{X }\). Because \(2(\varepsilon _0-\rho _M)\) is equal to \(\psi ^*(\varepsilon _0-2\rho _M)\), the extension problem (9.2) is soluble if and only if
is divisible by \(2\) in \(\mathcal{X }(T)\). If this is the case, the extension \(s^*=s_\gamma ^*\) is uniquely determined by the formula
This proves (ii). \(\square \)
We call \(\gamma \in \mathcal{X }(H)^c\) the character of the \(\mathbf{Spin}^c\)-structure \(\mathbf{P}_\gamma \). Let \(\gamma \in \mathcal{X }(H)^c\) and \(\chi \in \mathcal{X }(H)\). Then
so \(\gamma +2\chi \in \mathcal{X }(H)^c\). Thus we have an action of the abelian group \(\mathcal{X }(H)\) on the set of \(c\)-spinorial characters defined by \(\chi \cdot \gamma =\gamma +2\chi \). Let \(\mathbf{L}_\chi =G\times ^H\mathbf{C}_\chi \) be the homogeneous complex line bundle on \(M\) defined by \(\chi \in \mathcal{X }(H)\). Recall the natural isomorphisms
where \({\text{ Pic}}_G(M)\) denotes the (topological) Picard group of isomorphism classes of homogeneous complex line bundles on \(M\). The first map sends a character \(\chi \) to the class of the bundle \(\mathbf{L}_\chi \), and the second map sends the class of a bundle \(L\) to its equivariant Chern class \(c_G^1(L)\). (See e.g. [14, Theorem C.47].) A natural action of \({\text{ Pic}}_G(M)\) on \(\mathfrak Spin _G^c(M)\) is defined by
where \(\mathbf{U}(L)\) denotes the circle bundle associated with \(L\) and we identify the circle \(\mathbf{U}(1)\) with the kernel of \(\psi :\mathbf{Spin}^c(\mathfrak{m })\rightarrow \mathbf{SO}(\mathfrak{m })\). (The quotient in the right-hand side is taken in the category of manifolds over \(M\), and \(\mathbf{U}(1)_M=M\times \mathbf{U}(1)\) denotes the constant groupoid over \(M\) with fibre \(\mathbf{U}(1)\).)
Proposition 9.4
The notation is as in Proposition 9.3.
-
(i)
The bijection \(f:\mathcal{X }(H)^c\rightarrow \mathfrak Spin _G^c(M)\) is \(\mathcal{X }(H)\)-equivariant with respect to the group isomorphism (9.4).
-
(ii)
\(\mathfrak Spin _G^c(M)\) is a principal homogeneous space for the abelian group \(\mathcal{X }(H)\). In particular \(\mathfrak Spin _G^c(M)\) consists of at most one element if \(H\) is semisimple.
-
(iii)
Let \(\gamma \in \mathcal{X }(H)^c\). The determinant \(\text{ line}\) bundle of \(\mathbf{P}_\gamma \) is \(\mathbf{L}_\gamma =G\times ^H\mathbf{C}_\gamma \). Its equivariant Chern class \(c_1(\mathbf{L}_\gamma )\in H_G^2(M,\mathbf{Z})\cong \mathcal{X }(H)\) is equal to \(\gamma \).
-
(iv)
Let \(\gamma \in \mathcal{X }(H)^c\) and let
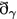 be the \(\mathbf{Spin}^c\) Dirac operator associated with \(\mathbf{P}_\gamma \). The equivariant Euler class of
be the \(\mathbf{Spin}^c\) Dirac operator associated with \(\mathbf{P}_\gamma \). The equivariant Euler class of  is
is 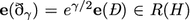 , where
, where  is the twisted \(\mathbf{Spin}^c\) Dirac operator of \(M\).
is the twisted \(\mathbf{Spin}^c\) Dirac operator of \(M\).
Proof
Let \(\gamma \in \mathcal{X }(H)^c\) and \(\chi \in \mathcal{X }(H)\). The fibre of \(\mathbf{U}(\mathbf{L}_\chi )\times ^{\mathbf{U}(1)_M}\mathbf{P}_\gamma \) over the identity coset \(\bar{1}\in M\) is
where \(\mathbf{U}(\mathbf{C}_\chi )\) denotes the unit circle in \(\mathbf{C}_\chi \). The map
defined by \((z,k)\mapsto zk\) is a diffeomorphism and is equivariant with respect to the \(H\)-actions defined on the left-hand side by
and on the right-hand side by \(h\cdot k=\hat{\eta }(s_{\gamma +2\chi }(h))k\). It follows that \([L_\chi ]\cdot [\mathbf{P}_\gamma ]=[\mathbf{P}_{\gamma +2\chi }]\), which proves (i). It is easy to verify that the \(\mathcal{X }(H)\)-action on \(\mathcal{X }(H)^c\) is free and transitive. Thus (ii) follows from (i). The determinant line bundle of \(\mathbf{P}_\gamma \) is
The isomorphism \(\mathcal{X }(H)\rightarrow H_G^2(M,\mathbf{Z})\) defined in (9.4) maps \(\gamma \) to \(c_G^1(\mathbf{L}_\gamma )\), which proves (iii). By (2.10) and (3.4), the Euler class of  is
is

where \(S\) is the spinor module of \(\mathbf{Cl}(\mathfrak{m })\). Using Lemma 3.2.1(iv) and (9.3) we obtain

which establishes (iv). \(\square \)
Example 9.5
(\(\mathbf{Spin}\)-structures) Let us call the orthogonal representation \(\eta :H\rightarrow \mathbf{SO}(\mathfrak{m })\), or the subgroup \(H\), spinorial if \(\eta \) lifts to a homomorphism \(\tilde{\eta }:H\rightarrow \mathbf{Spin}(\mathfrak{m })\). Thus, \(H\) is spinorial if and only if \(M\) has a \(G\)-invariant \(\mathbf{Spin}\)-structure, and such a structure is unique up to equivalence, because \(H\) is connected. A \(\mathbf{Spin}\)-structure determines a \(\mathbf{Spin}^c\)-structure by means of the homomorphism \(\kappa \circ \tilde{\eta }:H\rightarrow \mathbf{Spin}^c(\mathfrak{m })\), where \(\kappa :\mathbf{Spin}(\mathfrak{m })\rightarrow \mathbf{Spin}^c(\mathfrak{m })\) is the inclusion map. The corresponding \(c\)-spinorial character of \(H\) is \(\gamma =\det \circ \kappa \circ \tilde{\eta }=0\), because \(\mathbf{Spin}(\mathfrak{m })\) is the kernel of the determinant character. Hence, by Proposition 9.3(ii), \(M\) is \(G\)-invariantly \(\mathbf{Spin}\) if and only if \(\rho _M\in \mathcal{X }(T)\). The Euler class of the \(\mathbf{Spin}\) Dirac operator is equal to that of the twisted \(\mathbf{Spin}^c\) Dirac operator  .
.
Remark 9.6
If \(H\) is c-spinorial and semisimple, then a lifting \(H\rightarrow \mathbf{Spin}^c(\mathfrak{m })\) takes values in the commutator subgroup \(\mathbf{Spin}(\mathfrak{m })\), so \(H\) is spinorial.
Example 9.7
(almost complex structures) Up to homotopy, \(G\)-invariant almost complex structures on \(M\) correspond bijectively to \(H\)-invariant orthogonal complex structures on \(\mathfrak{m }\). Let \(J\) be such a structure; then the tangent representation \(\eta :H\rightarrow \mathbf{SO}(\mathfrak{m })\) takes values in \(\mathbf{U}(\mathfrak{m },J)\), the group of \(J\)-holomorphic orthogonal maps. We equip \(M\) with the \(\mathbf{Spin}^c\)-structure defined by composing this homomorphism with the canonical injection \(\iota \) (see e.g. [14, § D.3.1]),
The associated \(c\)-spinorial character \(\gamma \) is then \(\gamma =\det \circ \iota \circ \eta \). Since \(\det \circ \iota \) is equal to the usual complex determinant character of \(\mathbf{U}(\mathfrak{m },J)\), we have \(j_H^*(\gamma )=\sum _{k=1}^l\beta _k\), where the \(\beta _k\) are the weights of the \(T\)-action on \(\mathfrak{m }\) with respect to \(J\). To compute this, let \(\mathcal R _M^+=\{\alpha _1,\alpha _2, \ldots , \alpha _l\}\) and let \(J_0\) be the \(T\)-invariant complex structure on \(\mathfrak{m }\) given by the decomposition \(\mathfrak{m }=\bigoplus _{k=1}^l\mathfrak{m }_k\), where \(\mathfrak{m }_k\cong \mathfrak{g }_\mathbf{C}^{\alpha _k}\). On \(\mathfrak{m }_k\) we have \(J=c_kJ_0\), where \(c_k=\pm 1\). Hence \(\beta _k=c_k\alpha _k\) and \(j_H^*(\gamma )=\sum _{k=1}^lc_k\alpha _k\).
Example 9.8
(complex structures) As a special case of Example 9.7, let us take \(H\) to be the centralizer of a subtorus of \(T\). This is the case precisely when \(M\) has an integrable invariant almost complex structure, as one sees from the well-known identification \(M\cong G_\mathbf{C}{/}P\) ([8, § IX.4, Exercise 8]), where \(P\) is the parabolic subgroup of \(G_\mathbf{C}\) generated by \(H\) and the negative root spaces. The corresponding orthogonal almost complex structure \(J\) on \(\mathfrak{m }\) is positive with respect to the inner product on \(\mathfrak{m }\), so \(c_k=1\) for all \(k\) and hence

The Kähler structure on \(M\) and the associated \(\mathbf{Spin}^c\)-structure depend on the choice of the basis of \(\mathcal R _G\).
Rights and permissions
About this article
Cite this article
Landweber, G.D., Sjamaar, R. Character formulæ and GKRS multiplets in equivariant K-theory. Sel. Math. New Ser. 19, 49–95 (2013). https://doi.org/10.1007/s00029-012-0102-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00029-012-0102-6



 :
: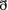 :
: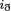 :
: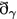 be the
be the  is
is 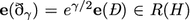 , where
, where  is the twisted
is the twisted