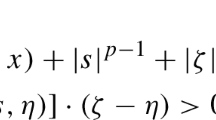Maximal regularity for elliptic operators with second-order discontinuous coefficients

Abstract

We prove maximal regularity for parabolic problems associated to the second-order elliptic operator

$$\begin{aligned} L =\Delta +(a-1)\sum _{i,j=1}^N\frac{x_ix_j}{|x|^2}D_{ij}+c\frac{x}{|x|^2}\cdot \nabla -b|x|^{-2} \end{aligned}$$

with $a>0$ and $b,\ c$ real coefficients.

1 Introduction

In this paper, we consider second-order elliptic operators of the form

$$\begin{aligned} L =\Delta +(a-1)\sum _{i,j=1}^N\frac{x_ix_j}{|x|^2}D_{ij}+c\frac{x}{|x|^2}\cdot \nabla -b|x|^{-2} \end{aligned}$$

(1)

with $a>0$ and $b,\ c$ constant real coefficients. The leading coefficients are uniformly elliptic but discontinuous at 0, if $a \ne 1$, and singularities in the lower order terms appear when b or c is different from 0. The operator commutes with dilations, in the sense that $I_s^{-1} LI_s=s^2L$, if $I_s u(x)=u(sx)$. When $c=0$ and $a=1$, L reduces to a Schrödinger operator with inverse square potential. Operators of this form have been widely investigated in previous works. In particular generation properties of analytic semigroups in $L^p$ spaces endowed with the Lebesgue measure, sharp kernel estimates and Rellich-type inequalities have been proved (see [3, 10,11,12,13,14,15,16]). Here, we prove that the following parabolic problem associated with L

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t u(t)-Lu(t)=f(t),&{}\quad t>0, \\ u(0)=0 \end{array}\right. \end{aligned}$$

(2)

has maximal $L^q$ regularity, that is for each $f\in L^q(0,\infty ;X)$ there exists $u\in W^{1,q}(0,\infty ;X)\cap L^q(0,\infty ; D(L))$ satisfying (2). Here, X is the underlying function space where L acts and D(L) is the domain of L in X.

The functional analytic approach we use for proving maximal regularity is widely described in [9] and in the new books [6, 7]. The whole theory relies on a deep interplay between harmonic analysis and structure theory of Banach spaces but largely simplifies when the underlying Banach spaces are $L^p$ spaces, by using classical square function estimates. This last approach has been employed extensively in [4], showing that uniformly parabolic operators have maximal regularity, under very general boundary conditions. Here, we show that the same happens for a class of degenerate second-order operators.

We deduce maximal regularity from the R-boundedness of the generated semigroup in closed sectors of the right half plane, see [4, Chapter 4]. This last is deduced through an extrapolation result in [1] which involves a family of Muckenhoupt weighted estimates. We show that L has maximal regularity in $L^p$ when it generates a semigroup in $L^p$, that is when the necessary and sufficient conditions of Theorems 2.1 and 2.2 are satisfied. We consider $L^p$ spaces with respect to radial power weights $|x|^m$ not just for the sake of generality but because our proof relies on weighted estimates: we are unable to obtain the result just fixing the Lebesgue measure or the symmetrizing measure but we have to work simultaneously in different homogeneous spaces. Our result is known for Schrödinger operators with inverse square potentials, due to a recent result of Bui, see [2]. We adopt his strategy in Sect. 4.1 but new complications arise due to the lack of symmetry of L in $L^p({\mathbb {R}}^N)$. At a first sight one could think that the symmetrizing measure (see Sect. 3) plays the same role as the Lebesgue measure for Schrödinger operators. This is not true, however, and there are situations where the symmetrizing measure is not doubling and the whole machinery of harmonic analysis in homogeneous spaces breaks down. Let us explain these points by considering Proposition 4.9. If $\mu _m$ is the Lebesgue measure, maximal regularity follows if L generates in $L^2$, which is not always the case since L is not symmetric. On the other hand, if $\mu _m$ is the symmetrizing measure $|x|^\gamma \mathrm{d}x$, one needs $N+\gamma >0$ in order to work with a doubling measure and this condition would impose extra conditions on the coefficients of L, not needed for the generation of a semigroup. The generality of the weights $|x|^m$ allows to play with an extra parameter m, prove maximal regularity when $|x|^m \mathrm{d}x$ is doubling and L generates both in $L^2(d\mu _m)$ and in $L^p(d\mu _m)$ and then recover the general situation by similarity transformations. When $|x|^m$ is doubling, that is when $m+N>0$, ${{{\mathcal {R}}}}$ boundedness follows from domination of the semigroup by maximal functions. Both the Euclidean maximal function ${\mathcal {M}} f$ and the weighted maximal function ${\mathcal {M}}_{\mu _m} f$ are used and the proof distinguish between $m \ge 0$ and $-N<m<0$, where $|x|^m\in A_p$.

The paper is organized as follows. In Sect. 2 we briefly recall generation results for the operator L in $L^p$ spaces with respect to the Lebesgue measure and sharp pointwise kernel estimates needed in the following. Then, in Sect. 3, we consider the same operators in weighted $L^p$ spaces with weights of the form $|x|^m$. A suitable transformation allows to deduce generation results and kernel estimates in weighted spaces from the previous ones. Section 4 is devoted to the main maximal regularity result.

Notation

We use $\Omega$ for ${\mathbb {R}}^N {\setminus }\{0\}$. The unit sphere $\{\Vert x\Vert =1\}$ in ${\mathbb {R}}^N$ is denoted by $S^{N-1}$. We denote by ${\mathbb {C}}_+:=\{z;\;\mathrm{Re}\,z>0\}$ and for $\delta \ge 0$, $\Sigma _\delta =\{z \in {\mathbb {C}}: |\mathrm{Arg} \, z | <\delta \}$. We adopt standard notation for $L^p$ and Sobolev spaces and the Lebesgue measure is understood when no measure is explicitly written.

2 Generation results in $L^p({\mathbb {R}}^N)$

In this section, we recall, without proofs, the main results concerning generation and domain characterization proved in [13, 15]. Kernel estimates are, instead, proved in [3, 11, 16].

If $1<p<\infty$, we define the maximal operator $L_{p,\mathrm{max}}$ through the domain

$$\begin{aligned} D(L_{p,\mathrm{max}})=\left\{ u \in L^p({\mathbb {R}}^N) \cap W^{2,p}_{\mathrm{loc}} ({\mathbb {R}}^N {\setminus }\{0\} ): Lu \in L^p({\mathbb {R}}^N)\right\} . \end{aligned}$$

(3)

The operator $L_{p,\mathrm{min}}$ is defined as the closure, in $L^p({\mathbb {R}}^N)$ of $(L,C_c^\infty ({\mathbb {R}}^N {\setminus }\{0\})$ (the closure exists since this operator is contained in the closed operator $L_{p,\mathrm{max}}$) and it is clear that $L_{p,\mathrm{min}} \subset L_{p,\mathrm{max}}$.

Let us employ spherical coordinates on ${\mathbb {R}}^N{\setminus }\{0\}$. For every $x\in {\mathbb {R}}^N{\setminus }\{0\}$ we write $x=r\omega$, where $r:=|x|$,  $\omega :=\frac{x}{|x|}\in {{\mathbb {S}}}^{N-1}$. If $u\in C^2({\mathbb {R}}^N)$, $D_r u$, $D_{rr} u$ are the radial derivatives of u and $\nabla _{\tau }u$ is the tangential component of its gradient. They are defined through the formulas

$$\begin{aligned} D_r u&=\sum _{i=1}^N D_{x_i}u\,\frac{x_i}{r},\quad D_{rr} u=\sum _{i,j=1}^N D_{x_ix_j}u\,\frac{x_i x_j}{r^2},\quad \nabla u=D_ru \frac{x}{|x|}+\frac{\nabla _\tau u}{r}. \end{aligned}$$

Denoting by $\Delta _0$ the Laplace–Beltrami operator on ${{\mathbb {S}}}^{N-1}$, the operator L takes the form

$$\begin{aligned} L=aD_{rr}+\frac{N-1+c}{r}D_r-\frac{b-\Delta _0}{r^2}. \end{aligned}$$

(4)

The equation $Lu=0$ has radial solutions $|x|^{-s_1}$, $|x|^{-s_2}$ where $s_1,s_2$ are the roots of the indicial equation $f(s)=-as^2+(N-1+c-a)s+b=0$ given by

$$\begin{aligned} s_1:=\frac{N-1+c-a}{2a}-\sqrt{D}, \quad s_2:=\frac{N-1+c-a}{2a}+\sqrt{D} \end{aligned}$$

(5)

where

$$\begin{aligned} D:= \frac{b}{a}+\left( \frac{N-1+c-a}{2a}\right) ^2. \end{aligned}$$

(6)

Introducing the parameter

$$\begin{aligned} \gamma =\frac{N-1+c}{a}-N+1. \end{aligned}$$

(7)

we may write

$$\begin{aligned} s_{1,2}&=\frac{N+\gamma -2}{2} \mp \sqrt{D},\quad D=\frac{b}{a} +\frac{\left( N+\gamma -2\right) ^2}{4}. \end{aligned}$$

The above numbers are real if and only if $D \ge 0$. In the critical case $D=0$, we often write $s_0$ for $s_1=s_2$. When $D<0$ the equation $u-Lu=f$ cannot have positive distributional solutions for certain positive f, see [15].

Assuming $D \ge 0$ we have shown in [13, 15] that there exists an intermediate operator $L_{p,\mathrm{min}} \subset L_{p,\mathrm{int}} \subset L_{p,\mathrm{max}}$ which generates a semigroup in $L^p({\mathbb {R}}^N)$ if and only if $\frac{N}{p} \in (s_1,s_2+2)$. From now on, we assume that $D\ge 0$ and $1<p<\infty$ throughout this paper.

Theorem 2.1

Assume that $D>0$. If $\frac{N}{p} \in (s_1,s_2+2)$ that is $s_1<\frac{N}{p}-2\theta <s_2$ for some $\theta \in (0,1]$, then L endowed with domain

$$\begin{aligned} D(L_{p,\mathrm{int}})=\{u\in D(L_{p,\mathrm{max}});\;|x|^{-2\theta }u\in L^p\} \end{aligned}$$

generates a bounded positive analytic semigroup of angle $\pi /2$ on $L^p$. Moreover,

$$\begin{aligned} D(L_{p,\mathrm{int}})= \{ u\in D(L_{p,\mathrm{max}});\; (1\wedge |x|)^{2-2\theta }D^2u, (1\wedge |x|)^{1-2\theta }\nabla u, |x|^{-2\theta }u\in L^p \} \end{aligned}$$

for all/one $\theta$ as above. In particular, if $s_1+2<\frac{N}{p}<s_2+2$, then $\theta =1$ and

$$\begin{aligned} D(L_{p,\mathrm{int}})= \{ u\in W^{2,p}({\mathbb {R}}^N);\; |x|^{-1}\nabla u, |x|^{-2}u\in L^p \}. \end{aligned}$$

When $\frac{N}{p} \not \in (s_1,s_2+2)$, then $\sigma (L)={\mathbb {C}}$ for every $L_{p,\mathrm{min}} \subset L \subset L_{p,\mathrm{max}}$.

Theorem 2.2

Assume that $D=0$. If $\frac{N}{p} \in (s_0, s_0+2)$, then L endowed with domain

$$\begin{aligned} D(L_{p,\mathrm{int}})= \left\{ u\in D(L_{p,\mathrm{max}});\; |x|^{-2\theta _0}|\log |x||^{-\frac{2}{p}}u \in L^p(B_{\frac{1}{2}}) \right\} \end{aligned}$$

with $\theta _0=\frac{1}{2}(s_0-\frac{N}{p})\in (0,1)$ generates a bounded positive analytic semigroup of angle $\pi /2$ on $L^p$. Moreover,

$$\begin{aligned} D(L_{p,\mathrm{int}})= \left\{ u\in D(L_{p,\mathrm{max}});\; \begin{array}{l} u\in W^{2,p}\left( {\mathbb {R}}^N{\setminus } B_{\frac{1}{2}}\right) ,\\ |x|^{2-2\theta _0}\left| \log |x|\right| ^{-\frac{2}{p}}D^2u\in L^p\left( B_{\frac{1}{2}}\right) ,\\ |x|^{1-2\theta _0}|\log |x||^{-\frac{2}{p}}\nabla u\in L^p\left( B_{\frac{1}{2}}\right) ,\\ |x|^{-2\theta _0}|\log |x||^{-\frac{2}{p}}u \in L^p\left( B_{\frac{1}{2}}\right) \end{array} \right\} . \end{aligned}$$

When $\frac{N}{p} \not \in (s_0,s_0+2)$, then $\sigma (L)={\mathbb {C}}$ for every $L_{p,\mathrm{min}} \subset L \subset L_{p,\mathrm{max}}$.

We refer the reader to [15, Theorem 3.29] for a detailed discussion of the inclusion $D(L_{p,\mathrm{int}}) \subset W^{2,p}({\mathbb {R}}^N)$. As a consequence of the previous results, L generates a semigroup in some $L^p({\mathbb {R}}^N)$, $1<p<\infty$, if and only if $(s_1,s_2+2)\cap {[0,N]}\ne \varnothing$. We remark that, in general, the generated semigroup is not contractive. If $a=1$, in fact, it is contractive if and only if $s_1 \le ( N-2)/p \le s_2$, see [13, Proposition 4.2].

The formal adjoint of L is given by

$$\begin{aligned} L^* =\Delta +(a-1)\sum _{i,j=1}^N\frac{x_ix_j}{|x|^2}D_{ij}+c^*\frac{x}{|x|^2}\cdot \nabla -b^*|x|^{-2} \end{aligned}$$

(8)

where $c^*=2(N-1)(a-1)-c$ and $b^*=b+(N-2)(c-(N-1)(a-1))$.

Let us compute the numbers $s_1^*,s_2^*,D^*$ defined as in (5), (6) and relative to $L^*$. We have

$$\begin{aligned} D^*&:= \frac{b^*}{a}+\left( \frac{N-1+c^*-a}{2a}\right) ^2=D, \end{aligned}$$

(9)

$$\begin{aligned} s_{1,2}^*&:=\frac{N-1+c^*-a}{2a}\mp \sqrt{D^*}=s_{1,2}+\frac{(a-1)(N-1)-c}{a}=N-2-s_{2,1}. \end{aligned}$$

(10)

Observe that $\frac{N}{p}>s_1$ is equivalent to $\frac{N}{p'} <s_2^*+2$ and $\frac{N}{p}<s_2$ is equivalent to $\frac{N}{p'} >s_1^*+2$. Similarly, $\frac{N}{p}>s_1+2$ is equivalent to $\frac{N}{p'} <s_2^*$ and $\frac{N}{p}<s_2+2$ is equivalent to $\frac{N}{p'} >s_1^*$.

L is formally self-adjoint, that is $L=L^*$, if and only if $c=(a-1)(N-1)$, that is when $\gamma =0$. Note also that $N-s_1^*=s_2+2$ and $s_2+2-s_1=2+2\sqrt{D}$. Moreover, $s_1+2\le s_2$ if and only if $D\ge 1$.

The coefficients of the formal adjoint $L^*$ of L, taken with respect to the Lebesgue measure and defined in (8), then satisfy

$$\begin{aligned} \gamma ^*=-\gamma ,\quad c^*=c-2a\gamma ,\quad b^*=b+a(N-2)\gamma ,\quad s_{1,2}^*=s_{1,2}-\gamma . \end{aligned}$$

(11)

Proposition 2.3

If p, q satisfy the hypotheses of Theorems 2.1 or 2.2, then the generated semigroups coincide in $L^p({\mathbb {R}}^N) \cap L^q({\mathbb {R}}^N)$. Moreover, $(L_{p,\mathrm{int}})^*=L^*_{p',\mathrm{int}}$.

In the following propositions we write the above results in a different way and we also clarify when $L_{p,\mathrm{int}}$ coincides with $L_{p,\mathrm{min}}$ or $L_{p,\mathrm{max}}$. To shorten the notation we write

$$\begin{aligned} \frac{N}{\alpha }:={\left\{ \begin{array}{ll} \frac{N}{\alpha },&{}\text {if}\quad \alpha >0,\\ \infty ,&{}\text {if}\quad \alpha \le 0, \end{array}\right. } \end{aligned}$$

(12)

Proposition 2.4

The following properties are equivalent

• (i) There exists an intermediate operator $L_{p,\mathrm{min}} \subset L_{p,\mathrm{int}} \subset L_{p,\mathrm{max}}$ which generates a semigroup on $L^p({\mathbb {R}}^N)$.

• (ii) $(s_1,s_2+2)\cap {[0,N]}\ne \varnothing$ and $\frac{N}{p}\in (s_1,s_2+2)$.

• (iii) $|x|^{-s_1},|x|^{-s_1^*}\in L^1_{\mathrm{loc}}\left( {\mathbb {R}}^N\right)$ that is $\displaystyle s_1,s_1^*<N$ and $\displaystyle \left( \frac{N}{s_1^*}\right) '<p<\frac{N}{s_1}$.

We now characterize $L_{p,\mathrm{int}}$ coincides with $L_{p,\mathrm{min}}$ or $L_{p,\mathrm{max}}$.

Proposition 2.5

If $D=0$ then $L_{p,\mathrm{min}}\subsetneq L_{p,\mathrm{int}}\subsetneq L_{p,\mathrm{max}}$, whereas if $D>0$ then

• $L_{ p,\mathrm{int}}=L_{p, \mathrm{max}}$ if and only if $\frac{N}{p}\in (s_1,s_2]$ or equivalently $\displaystyle \left( \frac{N}{s_1^*+2}\right) '\le p<\frac{N}{s_1}$;

• $L_{p,\mathrm{int}}=L_{p,\mathrm{min}}$ if and only if $\frac{N}{p}\in [s_1+2,s_2+2)$ or equivalently $\displaystyle \left( \frac{N}{s_1^*}\right) '<p\le \frac{N}{s_1+2}$.

Therefore, the following properties are equivalent:

• (i) $L_{p,\mathrm{int}}=L_{p, \mathrm{min}}=L_{p, \mathrm{max}}$;

• (ii) $D\ge 1$ and $\displaystyle \left( \frac{N}{s_1^*+2}\right) '\le p\le \frac{N}{s_1+2}$

• (iii) $s_1+2 \le s_2$ and $\frac{N}{p}\in [s_1+2,s_2]$.

Next we show that, under the assumptions of Theorems 2.1 and 2.2, the generated semigroup $e^{zL}$ consists of integral operators, see [3, 11].

For $z\in {\mathbb {C}}_+$, $x=r\omega$, $y=\rho \eta$, $r,\ \rho >0$, $|\omega |=|\eta |=1$, let

$$\begin{aligned} p_L(z, x,y)&:=\frac{1}{2az}\rho ^{\gamma }\left( r\rho \right) ^{-s_1-\sqrt{D}}\exp \left\{ -\frac{r^2+\rho ^2}{4az}\right\} \sum _{n=0}^\infty I_{\sqrt{D_n}}\left( \frac{r\rho }{2az}\right) {\mathbb {Z}}^{(n)}_{\omega }(\eta ). \end{aligned}$$

(13)

Here, $I_{\alpha }$ is the modified Bessel function of order $\alpha >0$, ${\mathbb {Z}}_\omega ^{(n)}$ is the zonal spherical harmonic of order $n\in {\mathbb {N}}_0$ and $D_n:=D+\frac{n(n+N-2)}{a}$.

Theorem 2.6

Assume that $p\in ]1,\infty [$ satisfies the condition of Proposition 2.4. Then,

$$\begin{aligned} e^{zL}f(x)=\int _{R^N}p_L(z,x,y)f(y)\mathrm{d}y,\quad \mathrm{Re}\,z>0,\ x,y\in \Omega ,\quad f\in L^p\left( {\mathbb {R}}^N\right) . \end{aligned}$$

(14)

Moreover, the following properties hold.

• (i) $p_L$ is analytic on ${\mathbb {C}}_+$, for every fixed $x, y\in \Omega$, it is continuous on ${\mathbb {C}}_+\times \Omega \times \Omega$ and $p_L|y|^{-\gamma }$ is symmetric on $\Omega \times \Omega$ for every fixed $z\in {\mathbb {C}}_+$. Furthermore, one has

  $$\begin{aligned} p_L(zs,x,y)=s^{-\frac{N}{2}}p_L\left( z,\frac{x}{\sqrt{s}}, \frac{y}{\sqrt{s}}\right) , \quad z\in {\mathbb {C}}_+,\quad s>0,\quad x, y\in {\mathbb {R}}^N {\setminus } \{0\}. \end{aligned}$$

• (ii) For every $\varepsilon >0$, there exist $C_\varepsilon >0$ and $\kappa _\epsilon >0$ such that for $z\in {\mathbb {C}}_+$ satisfying $|\arg z|\le \frac{\pi }{2}-\varepsilon$, and $(x,y)\in \Omega \times \Omega$

  $$\begin{aligned} | p_L(z,x,y)|&\le C_\varepsilon |z|^{-\frac{N}{2}} \left( \frac{|x|}{|z|^{\frac{1}{2}}}\wedge 1 \right) ^{-s_1} \left( \frac{|y|}{|z|^{\frac{1}{2}}}\wedge 1 \right) ^{-s_1^*} \exp \left( -\frac{|x-y|^2}{\kappa _\varepsilon |z|}\right) \\&\simeq C_\varepsilon |z|^{-\frac{N}{2}}\left( \frac{|x|}{|y|}\right) ^{-\frac{\gamma }{2}} \left( \frac{|x|}{|z|^{\frac{1}{2}}}\wedge 1 \right) ^{-s_1+\frac{\gamma }{2}} \left( \frac{|y|}{|z|^{\frac{1}{2}}}\wedge 1 \right) ^{-s_1+\frac{\gamma }{2}} \exp \left( -\frac{|x-y|^2}{\kappa _\varepsilon |z|}\right) . \end{aligned}$$

  where $s_1$ is defined in (5) and $s_1^*$ in (10).

• (iii) For every $1<p,q<\infty$ satisfying the condition of Proposition 2.4, the semigroups generated by L, respectively, in $L^p\left( {\mathbb {R}}^N\right)$ and in $L^q\left( {\mathbb {R}}^N\right)$ are consistent.

Proof

The existence of the heat kernel as well as its regularity is proved in [3, Theorems 4.3 and 4.5, Corollary 4.6] and in [16] (note that by [16, Lemma 5.4] the semigroups in $L^p\left( {\mathbb {R}}^N\right)$ and in $L^2\left( {\mathbb {R}}^N,|x|^\gamma \right)$, as well as their generators, are consistent). The decomposition (13) of $p_L$ in spherical harmonics is proved in [3, Theorem 4.3], [11, Proposition 6.7]. (ii) is proved in [3, Corollary 4.6]. The second inequality in (ii) can be proved as in [16, Corollary 4.15]. The consistency of $e^{zL}$ in all the spaces $L^p\left( {\mathbb {R}}^N\right)$ follows after observing that the kernel $p_L$ is independent of p. $\square$

In particular, when $s_1,\ s_1^*\le 0$ the heat kernel of the generated semigroup satisfies Gaussian estimates.

3 Generation results in $L^p({\mathbb {R}}^N,|x|^m\mathrm{d}x)$

In this section, we consider the operator L (keeping the assumption $D\ge 0$) in the space $L^p({\mathbb {R}}^M,d\mu _m)$ where $d\mu _m=|x|^m \mathrm{d}x$, $m\in {\mathbb {R}}$. The case $m=\gamma$, defined in (7), is important since this measure symmetrizes the operator and will be discussed at the end of this section. The weighted case is deduced by the unweighted one by the use of the following multiplication operator.

Proposition 3.1

For $k\in {\mathbb {R}}$, let

$$\begin{aligned} T_ku(x)&:=|x|^ku(x),\quad x\in \Omega . \end{aligned}$$

Then, $T_k$ maps isometrically $L^p(\Omega ,\mathrm{d}x)$ onto $L^p(\Omega ,|x|^{-kp}\mathrm{d}x)$. For every $u\in W^{2,1}_{\mathrm{loc}}\left( \Omega \right)$ one has

$$\begin{aligned} T_{-k} LT_ku={{\tilde{L}}} u \end{aligned}$$

where ${{\tilde{L}}}$ is the operator defined as in (1) with parameters b, c replaced, respectively, by

$$\begin{aligned} {{\tilde{b}}}=b-ak\left( N-2+\gamma +k\right) ,\quad {{\tilde{c}}}=c+2ak. \end{aligned}$$

(15)

Moreover, the discriminant ${{\tilde{D}}}$ and the parameter ${{\tilde{\gamma }}}$, ${{\tilde{s}}}_{1,2}$ of ${{\tilde{L}}}$ defined as in (5), (6) and (7) are given by

$$\begin{aligned} {{\tilde{D}}}=D,\quad {{\tilde{s}}}_{1,2}=s_{1,2}+k,\quad {{{\tilde{s}}}}^*_{1,2}= s^*_{1,2}-k,\quad {{\tilde{\gamma }}}=\gamma +2k. \end{aligned}$$

(16)

Proof

Employing spherical coordinates $x=r\omega$, $r=|x|$, $\omega =x/|x|\in {\mathbb {S}}^{N-1}$, we immediately get

$$\begin{aligned} D_r T_ku(x)&=r^{k}D_r u+kr^{k-1}u.\\ D_{rr} T_k u(x)&=r^{k}D_{rr} u+2kr^{k-1}D_r u+k(m-1)r^{k-2}u.\\ \Delta _0 T_ku(x)&=r^k\Delta _0 u. \end{aligned}$$

Then, recalling (4) one has

$$\begin{aligned} LT_ku(x)&=r^k\Big [aD_{rr} u+2akr^{-1}D_r u+ak(k-1)r^{-2}u\\&\quad +\frac{N-1+c}{r}\left( D_r u+kr^{-1}u\right) -\frac{b-\Delta _0}{r^2} \Big ]\\&=r^k\Big [aD_{rr} u+\frac{N-1+c+2ak}{r}D_r u\\&\quad -\Big (b-k(N-1+c+a(k-1))\Big )\frac{u}{r^2}+\frac{\Delta _0}{r^2} \Big ]\\&=T_k{{\tilde{L}}} u, \end{aligned}$$

which is the first required claim. The second assertion follows from the definitions (5), (6) since

$$\begin{aligned} {{\tilde{D}}}&=\frac{{{\tilde{b}}}}{a}+\left( \frac{N-1+{{\tilde{c}}}-a}{2a}\right) ^2 =\frac{b}{a}-k\left( N-2+\gamma +k\right) +\left( \frac{N-1+c-a+2ak}{2a}\right) ^2\\&=\frac{b}{a}-k\left( N-2+\gamma \right) -k^2+\left( \frac{N-1+c-a}{2a}+k\right) ^2\\&=D-k\left( N-2+\gamma \right) +k\frac{N-1+c-a}{a}= D. \end{aligned}$$

$\square$

If $1<p<\infty$, we define for $k=-m/p$

$$\begin{aligned} D(L_{m,p,\mathrm{max}}):=T_k\left( D({\tilde{L}}_{p,\mathrm{max}}) \right) , \quad D(L_{m,p,\mathrm{min}}):=T_k\left( D({\tilde{L}}_{p,\mathrm{min}}) \right) \end{aligned}$$

(17)

and

$$\begin{aligned} D(L_{m,p,\mathrm{int}})&:=T_k\left( D({\tilde{L}}_{p,\mathrm{int}}) \right) \nonumber \\&\quad =\left\{ u\in D(L_{m,p,\mathrm{max}});\;|x|^{-2\theta }u\in L^p\left( {\mathbb {R}}^N,d\mu _m\right) \right\} \end{aligned}$$

(18)

as one easily verifies (with the usual logarithmic correction when $D=0$). The operator $L_{m,p,\mathrm{min}}$ is the closure, in $L^p({\mathbb {R}}^N,d\mu _m)$ of $(L,C_c^\infty (\Omega ))$. We also define

$$\begin{aligned} W^{2,p}(\Omega ,d\mu _m)=\left\{ u\in L^1_{\mathrm{loc}}\left( \Omega \right) :u,\nabla u, D^2u\in L^p\left( \Omega ,d\mu _m\right) \right\} , \end{aligned}$$

where $\nabla u$, $D^2 u$ consist of weak derivatives of u in $\Omega$ (not in ${\mathbb {R}}^N$). For a fixed ball B centered at the origin, $W^{2,p}({\mathbb {R}}^N {\setminus } B,d\mu _m)$ is defined in a similar way.

In what follows we extend the result of the previous section by showing that L generates a semigroup in $L^p(\Omega ,d\mu _m)$ for any $1< p<\infty$ satisfying $s_1<\frac{N+m}{p}<s_2+2$. All the results for L in $L^p\left( {\mathbb {R}}^N,d\mu _m\right)$ are immediate consequence of those of ${\tilde{L}}$ in $L^p({\mathbb {R}}^N, \mathrm{d}x)$, using the isometry $T_{-m/p}$.

Theorem 3.2

Assume that $D>0$. If $\frac{N+m}{p} \in (s_1,s_2+2)$ that is $s_1<\frac{N+m}{p}-2\theta <s_2$ for some $\theta \in (0,1]$, then L endowed with domain

$$\begin{aligned} D(L_{m,p,\mathrm{int}})=\{u\in D(L_{m,p,\mathrm{max}});\;|x|^{-2\theta }u\in L^p\left( {\mathbb {R}}^N,d\mu _m\right) \} \end{aligned}$$

generates a bounded positive analytic semigroup of angle $\pi /2$ on $L^p\left( {\mathbb {R}}^N,d\mu _m\right)$. Moreover,

$$\begin{aligned} D(L_{m,p,\mathrm{int}})&= \Big \{ u\in D(L_{m,p,\mathrm{max}}): (1\wedge |x|)^{2-2\theta }D^2u, (1\wedge |x|)^{1-2\theta }\nabla u,\\&\qquad |x|^{-2\theta }u\in L^p\left( {\mathbb {R}}^N,d\mu _m\right) \Big \} \end{aligned}$$

for all/one $\theta$ as above. In particular, if $s_1+2<\frac{N+m}{p}<s_2+2$, then $\theta =1$ and

$$\begin{aligned} D(L_{m,p,\mathrm{int}})= \left\{ u\in W^{2,p}(\Omega ,d\mu _m);\; |x|^{-1}\nabla u, |x|^{-2}u\in L^p\left( {\mathbb {R}}^N,d\mu _m\right) \right\} . \end{aligned}$$

When $\frac{N+m}{p} \not \in (s_1,s_2+2)$, then $\sigma (L)={\mathbb {C}}$ for every $L_{m,p,\mathrm{min}} \subset L \subset L_{m,p,\mathrm{max}}$.

Theorem 3.3

Assume that $D=0$. If $\frac{N}{p} \in (s_0, s_0+2)$, then L endowed with domain

$$\begin{aligned} D(L_{m,p,\mathrm{int}})= \left\{ u\in D(L_{m,p,\mathrm{max}});\; |x|^{-2\theta _0}|\log |x||^{-\frac{2}{p}}u \in L^p(B_{\frac{1}{2}},d\mu _m) \right\} \end{aligned}$$

with $\theta _0=\frac{1}{2}(s_0-\frac{N}{p})\in (0,1)$ generates a bounded positive analytic semigroup of angle $\pi /2$ on $L^p\left( {\mathbb {R}}^N,d\mu _m\right)$. Moreover,

$$\begin{aligned} D(L_{m,p,\mathrm{int}})= \left\{ u\in D(L_{m,p,\mathrm{max}});\; \begin{array}{l} u\in W^{2,p}\left( {\mathbb {R}}^N{\setminus } B_{\frac{1}{2}},d\mu _m\right) ,\\ |x|^{2-2\theta _0}|\log |x||^{-\frac{2}{p}}D^2u\in L^p\left( B_{\frac{1}{2}},d\mu _m\right) ,\\ |x|^{1-2\theta _0}|\log |x||^{-\frac{2}{p}}\nabla u\in L^p\left( B_{\frac{1}{2}},d\mu _m\right) ,\\ |x|^{-2\theta _0}|\log |x||^{-\frac{2}{p}}u \in L^p\left( B_{\frac{1}{2}},d\mu _m\right) \end{array} \right\} . \end{aligned}$$

When $\frac{N+m}{p} \not \in (s_0,s_0+2)$, then $\sigma (L)={\mathbb {C}}$ for every $L_{m,p,\mathrm{min}} \subset L \subset L_{m,p,\mathrm{max}}$.

Let us denote by $I_{N+m}$ the closed interval with endpoints 0 and $N+m$ (note that $N+m <0$ is allowed). As a consequence of the previous Theorems, L generates a semigroup in some $L^p({\mathbb {R}}^N,d\mu _m)$, $1<p<\infty$, if and only if $(s_1,s_2+2)\cap I_{N+m}\ne \varnothing$.

In the following Proposition we compute the adjoint $L^{*m}$ of L with respect to the measure $\mu _m=|x|^m \mathrm{d}x$.

Proposition 3.4

The adjoint of $L_{m,p,\mathrm{int}}$ is $L^{*m}_{m,p',\mathrm{int}}$ where

$$\begin{aligned} L^{*m} =\Delta +(a-1)\sum _{i,j=1}^N\frac{x_ix_j}{|x|^2}D_{ij}+c^{*m}\frac{x}{|x|^2}\cdot \nabla -b^{*m}|x|^{-2} \end{aligned}$$

(19)

and

$$\begin{aligned} c^{*m}&=c-2a(\gamma -m)=c^*+2am,\\ b^{*m}&=b+a(N+m-2)(\gamma -m)=b^*+am(\gamma -m-N+2). \end{aligned}$$

The parameters $s_{1,2}^{*m},\gamma ^{*m},D^{*m}$ defined as in (5), (6) and relative to $L^{*m}$ are

$$\begin{aligned} D^{*m}=D,\quad \gamma ^{*m}=-\gamma +2m,\quad s_{1,2}^{*m}=s_{1,2}-\gamma +m =s_{1,2}^*+m. \end{aligned}$$

Proof

Note that if $1<p<\infty$ and $k\in {\mathbb {R}}$, then the adjoint operator of the isometry $T_k:L^p(\Omega ,\mathrm{d}x)\rightarrow L^p(\Omega ,|x|^{-kp}\mathrm{d}x)$ defined in Proposition 3.1 is the operator $T_k^*=T_{k(1-p)}$. In this way, since by definition $L=T_{-\frac{m}{p}}{{\tilde{L}}} T_{\frac{m}{p}}$, where ${{\tilde{L}}}$ is the operator acting on $L^p\left( {\mathbb {R}}^N\right)$ and defined by taking $k=-\frac{m}{p}$ in Proposition 3.1, one has

$$\begin{aligned} L^{*m}=\left( T_{\frac{m}{p}}\right) ^*\left( {{\tilde{L}}}\right) ^{*} \left( T_{-\frac{m}{p}}\right) ^*= T_{-\frac{m}{p'}}\left( {{\tilde{L}}}\right) ^{*} T_{\frac{m}{p'}}. \end{aligned}$$

The parameters of $L^{*m}$ can be computed using (11) and Proposition 3.1. The equality $(L_{m,p,\mathrm{int}})^{*m}=(L^{*m})_{m,p',\mathrm{int}}$ is consequence, via the isometry $T_{-\frac{m}{p'}}$, of the analogous property of ${\tilde{L}}^*$ in $L^{'p}({\mathbb {R}}^N, \mathrm{d}x)$ stated in Proposition 2.3. $\square$

Note that L is self-adjoint with respect to the measure $\mu _m=|x|^m \mathrm{d}x$ if and only if $m=\gamma$.

In the following Proposition we show an equivalent characterization of the range of p for which L generates a semigroup on $L^p\left( {\mathbb {R}}^N,d\mu _m\right)$.

In what follows when $N+m>0$ we adopt the notation

$$\begin{aligned} \frac{N+m}{\alpha }:={\left\{ \begin{array}{ll} \frac{N+m}{\alpha },&{}\text {if}\quad \alpha >0,\\ \infty ,&{}\text {if}\quad \alpha \le 0. \end{array}\right. } \end{aligned}$$

(20)

Proposition 3.5

The following properties are equivalent.

• (i) There exists an intermediate operator $L_{m,p,\mathrm{min}} \subset L_{m,p,\mathrm{int}} \subset L_{m,p,\mathrm{max}}$ which generates a bounded positive analytic semigroup of angle $\pi /2$ on $L^p({\mathbb {R}}^N,d\mu _m)$.

• (ii) $(s_1,s_2+2)\cap I_{N+m}\ne \varnothing$ and $\frac{N+m}{p}\in (s_1,s_2+2)$.

In particular:

• (a) When $N+m<0$ then (i) is equivalent to $s_1, s_1^{*m}<0$ and

  $$\begin{aligned} \frac{N+m}{s_1}<p<\left( \frac{N+m}{s_1^{*m}}\right) '. \end{aligned}$$

• (b) When $N+m=0$ then (i) is equivalent to $s_1, s_1^{*m}<0$ and $1<p<\infty$;

• (c) When $N+m>0$ then (i) is equivalent to $|x|^{-s_1},|x|^{-s_1^{*m}}\in L^1_{\mathrm{loc}}\left( {\mathbb {R}}^N,d\mu _m\right)$ that is $\displaystyle s_1,s_1^{*m}<N+m$ and

  $$\begin{aligned} \left( \frac{N+m}{s_1^{*m}}\right) '<p<\frac{N+m}{s_1}. \end{aligned}$$

Furthermore, $p=2$ satisfies the above assumptions if and only if $|\gamma -m|<2\left( 1+\sqrt{D}\right)$.

The coincidence of $L_{m,p,\mathrm{int}}$ with $L_{m,p,\mathrm{min}}$ or $L_{p,\mathrm{max}}$ can be obtained similarly from Proposition 2.5 but we do not state it here.

Let us compute the kernel of the generated semigroup

Proposition 3.6

Let $1<p <\infty$ satisfies the condition of Proposition 3.5. Then, for $z \in {\mathbb {C}}_+$

$$\begin{aligned} e^{zL}f(x)=\int _{R^N}p_m(z,x,y)f(y)d\mu _m(y),\quad t>0,\ x,y\in \Omega ,\quad f\in L^p\left( {\mathbb {R}}^N,d\mu _m\right) \end{aligned}$$

(21)

with $p_m(z,x,y)=|y|^{-m}p_L(z,x,y)$ and $p_L$ defined in (13). Moreover, the following properties hold

• (i) For every $\varepsilon >0$, there exist $C_\varepsilon >0$ and $\kappa _{\varepsilon }>0$ such that for $z\in {\mathbb {C}}_+$ satisfying $|\arg z|\le \frac{\pi }{2}-\varepsilon$, and $(x,y)\in \Omega \times \Omega$

  $$\begin{aligned} | p_m(z,x,y)| \le C_\varepsilon |z|^{-\frac{N}{2}}|y|^{-m} \left( \frac{|x|}{|z|^{\frac{1}{2}}}\wedge 1 \right) ^{-s_1} \left( \frac{|y|}{|z|^{\frac{1}{2}}}\wedge 1 \right) ^{-s_1^{*}} \exp \left( -\frac{|x-y|^2}{\kappa _\varepsilon |z|}\right) . \end{aligned}$$

  where $s_1$ is defined in (5), $s_1^*$ in (10) and $s_1^{*m}$ in Proposition 3.4. Furthermore, if $m\ge 0$ then

  $$\begin{aligned} | p_m(z,x,y)| \le C_\varepsilon |z|^{-\frac{N+m}{2}}\left( \frac{|x|}{|z|^{\frac{1}{2}}}\wedge 1 \right) ^{-s_1} \left( \frac{|y|}{|z|^{\frac{1}{2}}}\wedge 1 \right) ^{-s_1^{*m}} \exp \left( -\frac{|x-y|^2}{\kappa _\varepsilon |z|}\right) . \end{aligned}$$

• (iii) If $m,n\in {\mathbb {R}}$ and $1<p,q<\infty$ satisfy the generation conditions of Proposition 2.4 in both $L^p\left( {\mathbb {R}}^N,d\mu _m\right)$ and $L^q\left( {\mathbb {R}}^N,d\mu _n\right)$. Then, the semigroups generated by L in $L^q\left( {\mathbb {R}}^N,d\mu _m\right)$ and in $L^q\left( {\mathbb {R}}^N,d\mu _n\right)$ are consistent.

Proof

Let us consider the isometry $T_{-\frac{m}{p}}:L^p(\Omega ,\mathrm{d}x)\rightarrow L^p(\Omega ,|x|^{m}\mathrm{d}x)$. Then, by the definition, we have for every $u\in L^p(\Omega ,|x|^{m}\mathrm{d}x)$

$$\begin{aligned} e^{zL}u=T_{-\frac{m}{p}}\,e^{z{{\tilde{L}}}}\left( T_{\frac{m}{p}}u\right) \end{aligned}$$

where ${{\tilde{L}}}$ is the operator on $L^p\left( {\mathbb {R}}^N\right)$ defined as in (1) with parameters ${{\tilde{b}}},{{\tilde{c}}}$ defined by (15). Let p(z, x, y) the heat kernels of $\left( e^{zL}\right) _{z\in {\mathbb {C}}_+}$ on $L^p\left( {\mathbb {R}}^N,d\mu _m\right)$ taken with respect to the Lebesgue measure. The last relation between the semigroups translate into the analogous equality for the heat kernels:

$$\begin{aligned} p(z,x,y)=|x|^{-\frac{m}{p}}p_{{{\tilde{L}}}}(z,x,y)|y|^{\frac{m}{p}}. \end{aligned}$$

Recalling (13) and setting $x=r\omega$, $y=\rho \eta$, $r,\ \rho >0$, $|\omega |=|\eta |=1$, the last relation yields

$$\begin{aligned} p(z, x,y)&=\frac{1}{2at}r^{-\frac{m}{p}}\rho ^{{{\tilde{\gamma }}}+\frac{m}{p}}\left( r\rho \right) ^{-{{\tilde{s}}}_1-\sqrt{D}}\exp \left\{ -\frac{r^2+\rho ^2}{4az}\right\} \sum _{n=0}^\infty I_{\sqrt{D_n}}\left( \frac{r\rho }{2az}\right) {\mathbb {Z}}^{(n)}_{\omega }(\eta )\\&=\frac{1}{2at}r^{-\frac{m}{p}}\rho ^{\gamma -\frac{m}{p}}\left( r\rho \right) ^{-s_1+\frac{m}{p}-\sqrt{D}}\exp \left\{ -\frac{r^2+\rho ^2}{4az}\right\} \sum _{n=0}^\infty I_{\sqrt{D_n}}\left( \frac{r\rho }{2az}\right) {\mathbb {Z}}^{(n)}_{\omega }(\eta )\\&=p_L(z,x,y), \end{aligned}$$

where we used the fact that, from (16), we have ${{\tilde{D}}}=D$, ${{\tilde{s}}}_{1,2}=s_{1,2}+\frac{m}{p}$, ${{\tilde{\gamma }}}=\gamma -2\frac{m}{p}$. The other claims follow directly from Theorem 2.6. The estimate for $m\ge 0$ follows after observing that, in this case,

$$\begin{aligned} |y|^{-m}\left( |y|\wedge 1\right) ^{-s_1^{*m}+m}\le \left( |y|\wedge 1\right) ^{-s_1^{*m}}, \quad y\in \Omega . \end{aligned}$$

$\square$

Let us end this section with some comments on the special case $m=\gamma$, see (7). Writing

$$\begin{aligned} L= & {} |y|^{-\gamma }{ \text{ div }}\Big (|x|^{\gamma }\,{{\bar{a}}}(x)\nabla \Big )-b|x|^{-2},\\ {{\bar{a}}}(x)= & {} I_N+(a-1)\frac{x\otimes x}{|x|^2}, \end{aligned}$$

we can see that L is associated to the symmetric form

$$\begin{aligned} {\mathfrak {a}}(u,v) = \int _{{\mathbb {R}}^{N}} \left( \langle {{\bar{a}}}\nabla u ,\nabla v\rangle + b|y|^{-2}u v\right) \,d\mu _\gamma \end{aligned}$$

which is coercive if and only if $D \ge 0$. Then, L is self-adjoint in $L^2(d\mu _\gamma )$ and the generation conditions in $L^p(d\mu _\gamma )$ of Proposition 3.5 take the form

$$\begin{aligned} |(N+\gamma )(1/2-1/p)| < 1+\sqrt{D}. \end{aligned}$$

We refer to [3, 11, 16] for this approach.

4 Maximal regularity

An analytic semigroup $T(\cdot )$ on a Banach space X with generator B has maximal regularity of type $L^q$ ($1<q<\infty$) if for each $f\in L^q([0,T],X)$ the function $t\mapsto u(t)=\int _0^tT(t-s)f(s)\,ds$ belongs to $W^{1,q}([0,T],X)\cap L^q([0,T],D(B))$. This means that the mild solution of the evolution equation

$$\begin{aligned} u'(t)=Bu(t)+f(t), \quad t>0, \quad u(0)=0, \end{aligned}$$

is in fact a strong solution and has the best regularity one can expect. It is known that this property does not depend on $1<q<\infty$ and $T>0$. In recent years this concept has thoroughly been studied and applied in various directions, see [4, 9] for applications to uniformly parabolic problems under general boundary conditions. A characterization of maximal regularity is available in UMD Banach spaces, through the R-boundedness of the resolvent in sector larger than the right half plane or, equivalently, of the semigroup in a sector around the positive axis, can be largely simplified when $X=L^p$ (with respect to any measure), through the classical tool of square functions estimates. This is what we use and recall here after, see [9, Theorem 1.11, Remark 2.9]

Theorem 4.1

Let $T(\cdot )$ be a bounded analytic semigroup in $L^p$. Then, $T(\cdot )$ has maximal regularity of type $L^q$ if and only if there is a constant $C>0$ such that for every $z \in \Sigma _\delta$, $\delta >0$, $f_i \in L^p$

$$\begin{aligned} \left\| \left( \sum _i |T(z_i)f_i|^2\right) ^{\frac{1}{2}}\right\| _p \le C\left\| \left( \sum _i |f_i|^2\right) ^{\frac{1}{2}}\right\| _p. \end{aligned}$$

4.1 Muckenhoupt weighted estimates

Let $\left( S,d,\nu \right)$ be a space of homogeneous type, that is a metric space endowed with a Borel measure $\nu$ which is doubling on balls. When $X=L^p\left( S,d,\nu \right)$ the square function estimate in Theorem 4.1 can be reduced to a family of Muckenhoupt weighted estimates of the type

$$\begin{aligned} \Vert T(z)f\Vert _{L^p(w)}\le C \Vert f\Vert _{L^p(w)}, \end{aligned}$$

see Theorem 4.4 as follows. With this in mind, we recall preliminarily, the definition and the essential properties about Muckenhoupt weights. For the proof of the following results as well as for further details, we refer the reader to [1, Chapter 2 and 5] and [18, Chapter 1]. Let w be a weight, i.e., a nonnegative locally integrable function defined on S; we use the notation

Let ${\mathcal {M}}$ denote the uncentered maximal operator over balls in S defined by

(22)

where the supremum is taken over all balls of S containing x. We recall that ${\mathcal {M}}$ is bounded on $L^p(w)$ if and only if $w\in A_p$, see for example [5, Theorem 7.3].

We say that $w\in A_p$, $1< p <\infty$, if there exists a constant C such that for every ball $B\subseteq S$ one has

(23)

For $p=1$, we say that $w\in A_1$ if there is a constant C such hat ${\mathcal {M}}_\nu w\le C\,w$ a.e..

The weight w is in the reverse Hölder class of order q, $w\in RH_{q}$, $1< q \le \infty$, if there is a constant C such that for every ball $B\subseteq S$

with the usual modification for $q=\infty$. The best constants appearing in the previous inequalities are referred, respectively, as the $A_p$ and the $RH_q$ constants of w.

We sum up in the following propositions the properties we need about these classes of weights.

Proposition 4.2

The following properties hold:

• (i) $A_1\subset A_p \subset A_q$ for every $1\le p\le q\le \infty$;

• (ii) $w\in A_p$, $1<p<\infty$, if and only if $w^{1-p'}\in A_{p'}$;

• (iii) If $w\in A_p$, $1<p<\infty$, then there exists $1<q<p$ such that $w\in A_q$;

• (iv) $RH_\infty \subset RH_q\subset RH_p$ for $1 <p\le q\le \infty$;

• (v) If $w\in RH_q$, $1<q<\infty$, then there exists $q<p<\infty$ such that $w\in RH_p$;

• (vi) $A_\infty :=\bigcup _{1\le p<\infty } A_p=\bigcup _{1<q\le \infty } RH_q.$

• (vii) Let $1<p_0<p<q_0<\infty$. Then, we have

  $$\begin{aligned} w\in A_{\frac{p}{p_0}}\cap RH_{\left( \frac{q_0}{p}\right) '}\iff w^{-\frac{p'}{p}}=w^{1-p'}\in A_{\frac{p'}{q_0'}}\cap RH_{\left( \frac{p'_0}{p'}\right) '}. \end{aligned}$$

• (viii) If $1\le p\le \infty$ and $1\le r<\infty$ then

  $$\begin{aligned} w\in A_p \cap RH_r \quad \Longleftrightarrow \quad w^{r},w^{-\frac{1}{p-1}}\in A_{\infty } \quad \Longleftrightarrow \quad w^{r}\in A_{r\,(p-1)+1}. \end{aligned}$$

Proof

Properties (i)-(vi) can be found in [5, Chapter 7], [18, Chapter 1]. Point (vii) follows as in [1, Lemma 4.4]. The first equivalence in (viii) is proved in [18, Lemma 11, Chapter 1]; the second follows as in [8]. $\square$

A proof of the following result is in [18, Corollary 14] or [5, Chapter 7].

Lemma 4.3

Let $w\in A_p\cap RH_r$, $1< r,p<\infty$. Then, there exists a constant $C > 1$ such that for any ball B and any measurable subset $E\subset B$,

$$\begin{aligned} C^{-1}\left( \frac{\nu (E)}{\nu (B)}\right) ^p\le \frac{w(E)}{w(B)}\le C\left( \frac{\nu (E)}{\nu (B)}\right) ^{\frac{r-1}{r}}. \end{aligned}$$

We now state an extrapolation result originally due to Rubio de Francia, adapted as in [1, Theorem 4.9], which allows to reduce the square function estimate in Theorem 4.1 to a family of Muckenhoupt weighted estimates. Only weights and pairs of functions appear and no operator is involved. In what follows we consider families ${\mathcal {F}}=\{(f,g): f, g \in L_+^0(S) \}$, where $L_+^0(S)$ is the set of all nonnegative, measurable functions defined on S.

Theorem 4.4

Let $\left( S,d,\nu \right)$ be a space of homogeneous type and let ${\mathcal {F}} \subseteq L_+^0(S)\times L_+^0(S)$. Suppose that there exists p with $p_0\le p\le q_0$ (and $p<\infty$ if $q_0=\infty$), such that for $(f,g)\in {\mathcal {F}}$,

$$\begin{aligned} \Vert f\Vert _{L^p(w)} \le C\Vert g\Vert _{L^p(w)}, \quad \hbox {for all }w\in A_{\frac{p}{p_0}}\cap RH_{\left( \frac{q_0}{p}\right) '}, \end{aligned}$$

Then, for all $p_0<q<q_0$ and $(f,g)\in {\mathcal {F}}$ we have

$$\begin{aligned} \Vert f\Vert _{L^q(w)} \le C\,\Vert g\Vert _{L^q(w)}, \quad \text{ for } \text{ all } w\in A_{\frac{q}{p_0}}\cap RH_{\left( \frac{q_0}{q}\right) '}, \end{aligned}$$

Moreover, for all $p_0<q,r<q_0$ and $\{(f_j,g_j)\}\subset {\mathcal {F}}$ we have

$$\begin{aligned} \Big \Vert \Big (\sum _j (f_j)^r\Big )^{1/r} \Big \Vert _{L^q(w)} \le C\,\Big \Vert \Big (\sum _j (g_j)^r\Big )^{1/r} \Big \Vert _{L^q(w)}, \quad \hbox {for all }w\in A_{\frac{q}{p_0}}\cap RH_{\left( \frac{q_0}{q}\right) '}. \end{aligned}$$

All the constant C above may vary from line to line but depend only on the $A_p$ and $RH_q$ constants of w.

Combining Theorems 4.1 and 4.4 we derive the following characterization of maximal regularity in terms of boundedness over $L^p(w)$ spaces.

Theorem 4.5

Let $\left( S,d,\nu \right)$ be a space of homogeneous type and let $T(\cdot )$ be a bounded analytic semigroup in $L^p\left( S,\nu \right)$ defined in a sector $\Sigma _\delta$, $\delta >0$. Let $0<p_0<q_0\le \infty$. Suppose that $p_0<2<q_0$ and that there exists p with $p_0\le p\le q_0$ (and $p<\infty$ if $q_0=\infty$), such that for $f\in L^p\left( S,\nu \right)$,

$$\begin{aligned} \Vert T(z)f\Vert _{L^p(w)} \le C\Vert f\Vert _{L^p(w)},\quad \text{ for } \text{ all } z \in \Sigma _\delta , \quad \text{ for } \text{ all } w\in A_{\frac{p}{p_0}}\cap RH_{\left( \frac{q_0}{p}\right) '}, \end{aligned}$$

Then, for all $p_0<q<q_0$, $T(\cdot )$ has maximal regularity on $L^q(w)$ for all $w\in A_{\frac{q}{p_0}}\cap RH_{\left( \frac{q_0}{q}\right) '}$.

The following three lemmas will be crucial in the proof of maximal regularity.

Lemma 4.6

Let $w\in A_p$, $p \ge 1$, and let $\nu _w$ be the measure $wd\nu$. Denote by ${\mathcal {M}}_{\nu _w}$ and ${\mathcal {M}}_{\nu }$ the maximal function defined by $\nu _w$ and $\nu$. Then, $\left( S,d,\nu _w\right)$ is a space of homogeneous type and

$$\begin{aligned} {\mathcal {M}}_\nu f\le A_p (w)^\frac{1}{p}\left( {\mathcal {M}}_{\nu _w}|f|^p\right) ^{\frac{1}{p}}, \quad f\in L^1_{\mathrm{loc}}\left( S,\nu \right) , \end{aligned}$$

where $A_p(w)$ is the $A_p$ constant of w.

Proof

The doubling condition for the measure $\nu _w$ follows from that of $\nu$ and Lemma 4.3. To prove the second claim, let $f\in L^1_{\mathrm{loc}}\left( S,\nu \right)$. Then, for every ball B of S one has, applying Hölder’s inequality,

$$\begin{aligned} \frac{1}{\nu (B)}\int _B |f|d\nu&=\frac{1}{\nu (B)}\int _B |f|w^{\frac{1}{p}}w^{-\frac{1}{p}}d\nu \le \frac{1}{\nu (B)}\left( \int _B |f|^pwd\nu \right) ^{\frac{1}{p}}\left( \int _B w^{1-p'}d\nu \right) ^{\frac{1}{p'}}. \end{aligned}$$

Using (23) we get

$$\begin{aligned} \frac{1}{\nu (B)}\int _B |f|d\nu \le A_p(w)^\frac{1}{p}\left( \frac{1}{\nu _w(B)}\int _B |f|^pwd\nu \right) ^{\frac{1}{p}} \end{aligned}$$

which, taking the supremum over B, yields the required claim. The case $p=1$ follows similarly. $\square$

Lemma 4.7

Let p be a nonnegative, locally integrable function on ${\mathbb {R}}^N$ and consider the measure $\nu =p\, \mathrm{d}x$. Let $\mathcal {M_\nu }$ be the uncentered maximal operator relative to $\nu$, defined as in (22). If $0 \le \phi \in L^1\left( {\mathbb {R}}^N,\nu \right)$ is radial and decreasing then

$$\begin{aligned} |(\phi *pf)(x)|\le \Vert \phi \Vert _{L^1\left( {\mathbb {R}}^N,\nu \right) }{\mathcal {M}}_\nu f(x),\quad x\in {\mathbb {R}}^N,\quad f\in L^1_{\mathrm{loc}}\left( {\mathbb {R}}^N,\nu \right) . \end{aligned}$$

If p is homogeneous of degree k, i.e., $p(tx)=p(x)t^k$ for all $x\in {\mathbb {R}}^N$ and $t>0$, then setting $\phi _t:=t^{-N-k}\phi (t^{-1}x)$ one has

$$\begin{aligned} \sup _{ t>0}|(\phi _t*pf)(x)|\le \Vert \phi \Vert _{L^1\left( {\mathbb {R}}^N,\nu \right) }{\mathcal {M}}_\nu f(x). \end{aligned}$$

Proof

Let us suppose preliminarily that $\phi$ is a simple function and let us write, for some $a_1,\ldots ,a_k>0$ and balls $B_1,\ldots , B_k$ centered at 0,

$$\begin{aligned} \phi (x)=\sum _{j=1}^k a_j \chi _{B_{j}}(x). \end{aligned}$$

Then, since $\Vert \phi \Vert _{L^1\left( {\mathbb {R}}^N,\nu \right) }=\sum _{j=1}^k a_j\, \nu (B_{j})$ and $(\chi _{B_{j}}*pf)(x)=\int _{x-B_j}f(y)d\nu$, we get

$$\begin{aligned} (\phi *pf)(x)=\sum _{j=1}^k a_j\, \nu (B_{j})\frac{1}{\nu (B_{j})}(\chi _{B_{j}}*pf)(x)\le \Vert \phi \Vert _{L^1\left( {\mathbb {R}}^N,\nu \right) }{\mathcal {M}}_\nu f(x). \end{aligned}$$

In the general case the first required claim follows since $\phi$ can be approximated by a sequence of simple functions which increase to it monotonically. To prove the second claim it is enough to observe that, under the homogeneity assumptions on p, one has $\Vert \phi _t\Vert _{L^1\left( {\mathbb {R}}^N,\nu \right) }=\Vert \phi \Vert _{L^1\left( {\mathbb {R}}^N,\nu \right) }$ $\square$

Lemma 4.8

Let $m\in {\mathbb {R}}$ such that $N+m>0$ and let $d\mu _m=|x|^m \mathrm{d}x$. For every $k\in {\mathbb {R}}$ let us consider the radial weight $w(x)=|x|^k$. The following properties hold.

• (i) If $1\le p\le \infty$ then $w\in A_p\left( \mu _m\right)$ if and only if $-(N+m)<k<(N+m)(p-1)$.

• (ii) If $1\le p\le \infty$ and $1\le r<\infty$ then $w\in A_p(\mu _m) \cap RH_r(\mu _m)$ if and only if $-\frac{N+m}{r}<k<(N+m)(p-1)$.

Proof

To prove (i), we start by considering balls of center $x_0$ and radius 1. Fix $R>1$ and assume first that $|x_0|\le R$. Then, both $|x|^k$ and $|x|^{-\frac{k}{p-1}}$ are integrable in $B(x_0,1)$ with respect to the measure $\mu _m$ and

$$\begin{aligned} \left( \frac{1}{\mu _m(B(x_0,1))}\int _{B(x_0,1)}|x|^k\ d\mu _m\right) \left( \frac{1}{\mu _m(B(x_0,1))}\int _{B(x_0,1)}|x|^{-\frac{k}{p-1}}\ d\mu _m\right) ^{p-1}\le C\nonumber \\ \end{aligned}$$

(24)

for some positive constant C depending on R. On the other hand, when $|x_0|>R$, then

$$\begin{aligned}&\left( \frac{1}{\mu _m(B(x_0,1))}\int _{B(x_0,1)}|x|^k\ d\mu _m\right) \approx |x_0|^k, \\&\left( \frac{1}{\mu _m(B(x_0,1))}\int _{B(x_0,1)}|x|^{-\frac{k}{p-1}}\ d\mu _m\right) ^{p-1}\approx |x_0|^{-k} \end{aligned}$$

and the left hand side in (24) is bounded from above and below by a constant. For a general ball of radius r the claim follows by scaling. Property (ii) follows using (i) and property (viii) of Proposition 4.2. $\square$

4.2 Maximal regularity when $N+m>0$

Let $m\in {\mathbb {R}}$ be such that $N+m>0$ and let us consider the measure $d\mu _m=|x|^m \mathrm{d}x$ on ${\mathbb {R}}^N$. Denoting by d the Euclidean distance, $\left( {\mathbb {R}}^N,d,\mu _m\right)$ is of homogeneous type. In what follows we write $A_p(\mu _m)$, $RH_p(\mu _m)$, ${\mathcal {M}}_{\mu _m}$ to denote, respectively, the class of Muckenhoupt weights, the reverse Hölder class and the maximal function over balls taken with respect to the measure $\mu _m$. When $m=0$ we write $A_p$, $RH_p$, ${\mathcal {M}}$.

We fix $0<\delta <\pi /2$ and we recall that for $z \in \Sigma _\delta$, $z=\omega t$, $t=|z|$, Proposition 3.6 yields the pointwise estimate

$$\begin{aligned} |T(z)f(x)|&\le C t^{-\frac{N}{2}}\,\left( \frac{|x|}{\sqrt{t}}\wedge 1 \right) ^{-s_1}\int _{{\mathbb {R}}^N} \left( \frac{|y|}{\sqrt{t}}\wedge 1 \right) ^{-s_1+\gamma } \nonumber \\&\quad \exp \left( -\frac{|x-y|^2}{\kappa t}\right) |f(y)| \,\mathrm{d}y. \end{aligned}$$

(25)

When $m\ge 0$ we also have

$$\begin{aligned} |T(z)f(x)|&\le C t^{-\frac{N+m}{2}}\,\left( \frac{|x|}{\sqrt{t}}\wedge 1 \right) ^{-s_1}\int _{{\mathbb {R}}^N} \left( \frac{|y|}{\sqrt{t}}\wedge 1 \right) ^{-s_1^{*m}} \nonumber \\&\quad \exp \left( -\frac{|x-y|^2}{\kappa t}\right) |f(y)| \,d\mu _m(y). \end{aligned}$$

(26)

We prove the ${\mathcal {R}}$-boundedness of the family $(T(z))_{z \in \Sigma _\delta }$ using the extrapolation result of Theorem 4.4. We follow the proof in [2, Theorem 2.9] but new complications arise because the operator is non-symmetric and the measure $\mu _m$ is not the Lebesgue one. In particular we have to distinguish between the cases $m \ge 0$ and $-N<m<0$ and both the maximal functions with respect to the Lebesgue measure and the weighted one appear.

For the reader’s convenience, in what follows we write for $z\in \Sigma _\delta$, $B=B(0,\sqrt{t})$, $t=|z|$, and

$$\begin{aligned} T(z)f&=\chi _{B^c}\left( T(z)f\chi _{B^c}\right) +\chi _{B}\left( T(z)(f\chi _{B})\right) +\chi _{B^c}\left( T(z)f\chi _B\right) +\chi _{B}\left( T(z)(f\chi _{B^c})\right) \nonumber \\&:= T_1(z)f+T_2(z)f+T_3(z)f+T_4(z)f. \end{aligned}$$

(27)

Proposition 4.9

Let $N+m>0$, $1<p< \infty$ and let us suppose that the generation conditions of Proposition 3.5 are satisfied, that is

$$\begin{aligned} s_1,s_1^{*m}<N+m, \quad \left( \frac{N+m}{s_1^{*m}}\right) '<p<\frac{N+m}{s_1}. \end{aligned}$$

(28)

Then, for every weight

$$\begin{aligned} w\in A_{\frac{p}{\left( \frac{N+m}{s_1^{*m}}\right) '}}(\mu _m)\cap RH_{\left( \frac{N+m}{s_1 p}\right) '}(\mu _m) \end{aligned}$$

there exist $C>0$ depending on $\delta$ and the $A_p(\mu _m)$ and $R_p(\mu _m)$ constants of w such that for every $z\in \Sigma _\delta$ one has

$$\begin{aligned} \Vert T(z)f\Vert _{L^p(w)}\le C\Vert f\Vert _{L^p(w)},\quad f\in L^p({\mathbb {R}}^N,w d\mu _m)=:L^p(w). \end{aligned}$$

Finally, if $|\gamma -m|<2\left( 1+\sqrt{D}\right)$ then $T(\cdot )$ has maximal regularity on $L^p({\mathbb {R}}^N,w d\mu _m)$.

We split the proof in four lemmas according to (27).

Lemma 4.10

The estimate of Proposition 4.9 holds for $(T_1(z))_{z \in \Sigma _\delta }$.

Proof

Assume first that $m\ge 0$. Then, using (26) and Lemma 4.7 with $p(y)=|y|^m$ we get

$$\begin{aligned} |T_1(z)f(x)|&\le C t^{-\frac{N+m}{2}}\int _{{\mathbb {R}}^N} \exp \left( -\frac{|x-y|^2}{\kappa t}\right) |f(y)| \,d\mu _m(y)\le C{\mathcal {M}}_{\mu _m}f(x), \end{aligned}$$

The claim then follows since ${\mathcal {M}}_{\mu _m}$ is bounded on $L^p(w)$.

When $-N<m<0$ we use (25) (and Lemma 4.7 with respect to the Lebesgue measure) to get

$$\begin{aligned} |T_1(z)f(x)|&\le C t^{-\frac{N}{2}}\int _{{\mathbb {R}}^N} \exp \left( -\frac{|x-y|^2}{\kappa t}\right) |f(y)|\chi _{B^c} (y)\,\mathrm{d}y\le C{\mathcal {M}}f(x), \end{aligned}$$

Since $w\in A_{\frac{p}{\left( \frac{N+m}{s_1^{*m}}\right) '}}(\mu _m)$, by Proposition 4.2 there exists r sufficiently close to $\left( \frac{N+m}{s_1^{*m}}\right) '$ such that $\left( \frac{N+m}{s_1^{*m}}\right) '<r<p<\frac{N+m}{s_1}$ and $w\in A_{\frac{p}{r}}(\mu _m)$. Since $-N<m<0$, Lemma 4.8 (i) gives $|x|^m\in A_r(\mathrm{d}x)$ and then Lemma 4.6 yields

$$\begin{aligned} |T_1(z)f(x)|&\le C\left( {\mathcal {M}}_{\mu _m}|f|^{r}(x)\right) ^{\frac{1}{r} }. \end{aligned}$$

Since $w\in A_{\frac{p}{r}}(\mu _m)$, ${\mathcal {M}}_{\mu _m}$ is bounded on $L^{\frac{p}{r}}(w)$ and we get $\Vert T_1(z)f\Vert _{L^p(w)}\le C\Vert f\Vert _{L^p(w)}$. $\square$

Lemma 4.11

The estimate of Proposition 4.9 holds for $(T_2(z))_{z \in \Sigma _\delta }$.

Proof

Using (25) and Hölder’s inequality we get

$$\begin{aligned} |T_2(z)f(x)|&\le C t^{-\frac{N+m}{2}}\left( \frac{|x|}{\sqrt{t}}\right) ^{-s_1}\int _{B} \left( \frac{|y|}{\sqrt{t}}\right) ^{-s_1^{*m}} |f(y)| \,d\mu _m(y) \\&\le Ct^{-\frac{N+m}{2}}\left( \frac{|x|}{\sqrt{t}}\right) ^{-s_1}\Vert f\Vert _{L^p(w)} \left( \int _{B}\left( \frac{|y|}{\sqrt{t}} \right) ^{-s_1^{*m}p'}w(y)^{1-p'}\ d\mu _m(y)\right) ^{\frac{1}{p'}}. \end{aligned}$$

Setting $v=w^{1-p'}$ this implies

$$\begin{aligned} \Vert T_2(z)f\Vert _{L^p(w)}^p&\le Ct^{-\frac{N+m}{2}p}\Vert f\Vert _{L^p(w)}^p \left( \int _{B}\left( \frac{|y|}{\sqrt{t}} \right) ^{-s_1^{*m}p'}v(y)\ d\mu _m(y)\right) ^{\frac{p}{p'}} \\&\quad \int _{B} \left( \frac{|x|}{\sqrt{t}}\right) ^{-s_1 p}w(x)\ d\mu _m(x). \end{aligned}$$

Let us treat the first integral. If $s_1^{*m}>0$, then one has

$$\begin{aligned} \int _{B}\left( \frac{|y|}{\sqrt{t}} \right) ^{-s_1^{*m}p'}v(y)\ d\mu _m(y)&=\sum _{j\ge 0}\int _{2^{-j-1}\le \frac{|y|}{\sqrt{t}}<2^{-j}}\left( \frac{|y|}{\sqrt{t}} \right) ^{-s_1^{*m}p'}v(y)\ d\mu _m(y)\\&\le C \sum _{j\ge 0} 2^{js_1^{*m}p'}v(2^{-j}B). \end{aligned}$$

By property (vii) of Proposition 4.2, $v\in A_{\frac{p'}{\left( \frac{N+m}{s_1}\right) '}}\cap RH_{\left( \frac{N+m}{s_1^{*m} p'}\right) '}$; by property (v) of Proposition 4.2 there exists $r>p'$ such that $v\in RH_{\left( \frac{N+m}{s_1^{*m} r}\right) '}$. Lemma 4.3 then implies

$$\begin{aligned} v(2^{-j}B)\le C v(B)\left( \frac{\mu _m\left( 2^{-j}B\right) }{\mu _m\left( B\right) }\right) ^{\frac{s_1^{*m} r}{N+m}}=C v(B)2^{-jrs_1^{*m}}. \end{aligned}$$

Therefore, since $s_1^{*m}> 0$

$$\begin{aligned} \int _{B}\left( \frac{|y|}{\sqrt{t}} \right) ^{-s_1^{*m}p'}v(y)\ d\mu _m(y)&\le Cv(B) \sum _{j\ge 0} 2^{-js_1^{*m}(r-p')}=Cv(B). \end{aligned}$$

The last inequality holds also when $s_1^{*m}\le 0$, since in this case

$$\begin{aligned} \int _{B}\left( \frac{|y|}{\sqrt{t}} \right) ^{-s_1^{*m}p'}v(y)\ d\mu _m(y)\le \int _{B}v(y)\ d\mu _m(y)=v(B). \end{aligned}$$

Similarly if $s_1>0$ then

$$\begin{aligned} \int _{B} \left( \frac{|x|}{\sqrt{t}}\right) ^{-s_1 p}w(x)\ d\mu _m(x)&=\sum _{j\ge 0}\int _{2^{-j-1}\le \frac{|x|}{\sqrt{t}}<2^{-j}}\left( \frac{|x|}{\sqrt{t}}\right) ^{-s_1p}w(x)\ d\mu _m(x)\\&\le C \sum _{j\ge 0} 2^{js_1p}w(2^{-j}B). \end{aligned}$$

Since $w\in A_{\frac{p}{\left( \frac{N+m}{s_1^{*M}}\right) '}}\cap RH_{\left( \frac{N+m}{s_1 p}\right) '}$ by property (v) of Proposition 4.2 there exists $r>p$ such that $w\in RH_{\left( \frac{N+m}{s_1 r}\right) '}$. By Lemma 4.3 then

$$\begin{aligned} w(2^{-j}B)\le C w(B)2^{-jrs_1}. \end{aligned}$$

Therefore

$$\begin{aligned} \int _{B}\left( \frac{|x|}{\sqrt{t}} \right) ^{-s_1p}w(x)\ d\mu _m(x)\le C w(B) \sum _{j\ge 0} 2^{-js_1(r-p)}=Cw(B). \end{aligned}$$

The last inequality holds also when $s_1^{}\le 0$, since in this case

$$\begin{aligned} \int _{B}\left( \frac{|x|}{\sqrt{t}} \right) ^{-s_1}w(x)\ d\mu _m(x)\le \int _{B}w(x)\ d\mu _m(x)=w(B). \end{aligned}$$

Putting together the last inequalities we have in any case

$$\begin{aligned} \Vert T_2(z)f\Vert _{L^p(w)}^p\le C \Vert f\Vert _{L^p(w)}^p t^{-p\frac{N+m}{2}}\left( v(B)\right) ^{\frac{p}{p'}}w(B). \end{aligned}$$

Since $s_1^{*m}<N+m$ from property (i) of Proposition 4.2 we get $w\in A_{\frac{p}{\left( \frac{N+m}{s_1^{*m}}\right) '}}\subseteq A_p$ which implies, by the definition (23) of $A_p$ weights, $\sup _{ t >0}t^{-p\frac{N+m}{2}}\left( v(B)\right) ^{\frac{p}{p'}}w(B) <\infty$. $\square$

Lemma 4.12

The estimate of Proposition 4.9 holds for $(T_3(z))_{z \in \Sigma _\delta }$.

Proof

Using (25) we get

$$\begin{aligned} |T_3(z)f(x)|&\le C t^{-\frac{N+m}{2}}\int _{B} \left( \frac{|y|}{\sqrt{t}} \right) ^{-s_1^{*m}} \exp \left( -\frac{|x-y|^2}{\kappa t}\right) |f(y)| \,d\mu _m(y). \end{aligned}$$

Let us fix r such that $\left( \frac{N+m}{s_1^{*m}}\right) '<r<p<\frac{N+m}{s_1}$. Applying Hölder’s inequality we obtain

$$\begin{aligned} |T_3(z)f(x)|&\le C \left( t^{-\frac{N+m}{2}} \int _{{\mathbb {R}}^N} \exp \left( -\frac{|x-y|^2}{\kappa t}\right) |f(y)|^r\ d\mu _m(y)\right) ^\frac{1}{r} \\&\quad \times \left( t^{-\frac{N+m}{2}} \int _{B}\left( \frac{|y|}{t^{\frac{1}{2}}} \right) ^{-s_1^{*m}r'} \ d\mu _m(y)\right) ^\frac{1}{r'}. \end{aligned}$$

The substitution $z=y/\sqrt{t}$ and Lemma 4.7 yield

$$\begin{aligned} |T_3(z)f(x)|&\le C \left( {\mathcal {M}}_{\mu _m}|f|^r(x)\right) ^{\frac{1}{r}} \left( \int _{B(0,1)}|z|^{-s_1^{*m}r'+m}\ \mathrm{d}z\right) ^\frac{1}{r'}=C \left( {\mathcal {M}}_{\mu _m}|f|^r(x)\right) ^{\frac{1}{r}} \end{aligned}$$

Since $w\in A_{\frac{p}{\left( \frac{N+m}{s_1^{*m}}\right) '}}$, by Proposition 4.2 there exists r sufficiently close to $\left( \frac{N+m}{s_1^{*m}}\right) '$ such that $\left( \frac{N+m}{s_1^{*m}}\right) '<r<p<\frac{N+m}{s_1}$ and $w\in A_{\frac{p}{r}}$. This implies that ${\mathcal {M}}_{\mu _m}$ is bounded on $L^{\frac{p}{r}}(w)$ which, using the latter inequality, proves the required claim. $\square$

To prove the boundedness of $T_4(z)$ we apply a duality argument. With this aim, let p, m satisfy the assumptions in (28) and let $T^{*m}(z)$ be the adjoint of T(z) taken with respect to the measure $\mu _m$. The conditions in (28) are equivalent to

$$\begin{aligned} s_1,s_1^{*m}<N+m, \quad \frac{N+m}{s_1}<p'<\left( \frac{N+m}{s_1^{*m}}\right) '. \end{aligned}$$

If $L^{*m}$ is the adjoint operator defined by Proposition 3.4, then the last conditions assures that $L^{*m}$ generates a bounded analytic semigroup in $L^{p'}\left( {\mathbb {R}}^N,\mu _m\right)$ which coincides with $T^{*m}(z)$.

Lemma 4.13

The estimate of Proposition 4.9 holds for $(T_4(z))_{z \in \Sigma _\delta }$.

Proof

We apply a duality argument. Let $g\in L^{p'}({\mathbb {R}}^N,w\mu _m)$; since $T_4(z)=T^{*m}_3(z)$ we obtain

$$\begin{aligned} \int _{{\mathbb {R}}^N}T_4(z)fg\, w\mu _m=\int _{{\mathbb {R}}^N}f\,T^{*m}_3(z)(g w)\mu _m=\int _{{\mathbb {R}}^N}f\,\frac{T^{*m}_3(z)(g w)}{w}w\mu _m. \end{aligned}$$

Using Hölder’s inequality we then yield

$$\begin{aligned} \left| \int _{{\mathbb {R}}^N}T_4(z)fg\, w\mu _m\right|&\le \Vert f\Vert _{L^p(\omega )}\left\| \frac{T^{*m}_3(z)(g w)}{w}\right\| _{L^{p'}(\omega )}\\&=\Vert f\Vert _{L^p(\omega )}\left\| T^{*m}_3(z)(g w)\right\| _{L^{p'}(\omega ^{1-p'})}. \end{aligned}$$

Using Lemma 4.12 with L and p replaced, respectively, by $L^{*m}$ and $p'$ we get

$$\begin{aligned} \left| \int _{{\mathbb {R}}^N}T_4(z)fg\, w\mu _m\right| \le C\Vert f\Vert _{L^p(\omega )}\left\| g w\right\| _{L^{p'}(\omega ^{1-p'})}=C\Vert f\Vert _{L^p(\omega )}\left\| g \right\| _{L^{p'}(\omega )} \end{aligned}$$

which concludes the proof. $\square$

We can finally prove Proposition 4.9.

Proof of Proposition 4.9

The first claim follows by using (27) and Lemmas 4.10, 4.11, 4.12, 4.13. If $|\gamma -m|<2\left( 1+\sqrt{D}\right)$ then the ${\mathcal {R}}$-boundedness of $(T(z))_{z \in \Sigma _\delta }$ on $L^p({\mathbb {R}}^N,w d\mu _m)$ follows by Theorems 4.1, 4.5 since, in this case, by Proposition 3.5, $p=2$ satisfies (28). $\square$

4.3 Maximal regularity without restrictions on m

Let us start with the case of the Lebesgue measure, that is when $m=0$.

Theorem 4.14

Let $1<p< \infty$ and let us suppose that the generation conditions of Proposition 2.4 are satisfied, that is

$$\begin{aligned} s_1,s_1^{*}<N, \quad \left( \frac{N}{s_1^{*}}\right) '<p<\frac{N}{s_1}. \end{aligned}$$

Then, $T(\cdot )$ has maximal regularity on $L^p({\mathbb {R}}^N)$.

Proof

Let $s_1<\frac{N}{p}<s_2+2$. If $|\gamma |<2\left( 1+\sqrt{D}\right)$, the required claim follows by using Proposition 4.9 with $m=0$ and $w=1$. Let us suppose now $|\gamma |\ge 2\left( 1+\sqrt{D}\right)$; in this case, from Proposition 3.5, L does not generate a semigroup in $L^2\left( {\mathbb {R}}^N\right)$ and therefore $p\ne 2$. Let $m\in {\mathbb {R}}$ and let us consider the isometry

$$\begin{aligned} T_{\frac{m}{p}}: L^p(\Omega ,|x|^m \mathrm{d}x)\rightarrow L^p(\Omega ,\mathrm{d}x),\quad u\mapsto |x|^{\frac{m}{p}}u. \end{aligned}$$

Using Proposition 3.1 we have

$$\begin{aligned} T_{-\frac{m}{p}} LT_{\frac{m}{p}}u={{\tilde{L}}} u \end{aligned}$$

where ${{\tilde{L}}}$ is the operator defined as in (1) with parameters b, c defined by (15); in particular we have ${{\tilde{\gamma }}}=\gamma +2\frac{m}{p}$. Let ${{\tilde{T}}}(z)=T_{-\frac{m}{p}} T(z)T_{\frac{m}{p}}$ be the analytic semigroup generated by ${\tilde{L}}$. From the latter equality one can easily deduce that $(T(z))_{z \in \Sigma _\delta }$ is ${\mathcal {R}}$-bounded on $L^p({\mathbb {R}}^N)$ if and only if there exists $m\in {\mathbb {R}}$ such that $({{\tilde{T}}}(z))_{z \in \Sigma _\delta }$ is ${\mathcal {R}}$-bounded on $L^p({\mathbb {R}}^N, |x|^m\mathrm{d}x)$. From Proposition 4.9 this is equivalent to require

$$\begin{aligned} \left| \gamma +m\left( \frac{2}{p}-1\right) \right| =|{{\tilde{\gamma }}} -m|<2\left( 1+\sqrt{D}\right) , \quad N+m>0, \end{aligned}$$

(note that, by construction, the generation conditions for ${\tilde{L}}$ in $L^p({\mathbb {R}}^N, |x|^m\mathrm{d}x)$ are implicitly satisfied). By elementary calculation the latter inequalities read as

$$\begin{aligned} {\left\{ \begin{array}{ll} N+m>0;\\ m\left( \frac{1}{p}-\frac{1}{2}\right) <\frac{N}{2}-s_1;\\ m\left( \frac{1}{p}-\frac{1}{2}\right) >\frac{N}{2}-(s_2+2), \end{array}\right. } \end{aligned}$$

If $p<2$ the system has a solution m when

$$\begin{aligned} \frac{N}{2} -(s_2+2)<-N\left( {\frac{1}{p} -\frac{1}{2}}\right) <\frac{N}{2} -s_1 \end{aligned}$$

that is when $s_1<\frac{N}{p} <s_2+2$. If $p>2$ the claim follows in the same way. $\square$

The results for L in $L^p\left( {\mathbb {R}}^N,d\mu _m\right)$ are immediate consequence of those of ${\tilde{L}}$ in $L^p({\mathbb {R}}^N, \mathrm{d}x)$, using the isometry $T_k$ of Proposition 3.1 with $k=-m/p$ and Theorem 4.14. Note that the condition $N+m>0$ is no longer required.

Corollary 4.15

Let $m\in {\mathbb {R}}$, $1<p< \infty$ and let us suppose that the generation conditions of Proposition 3.5 are satisfied, that is

$$\begin{aligned} (s_1,s_2+2)\cap I_{N+m}\ne \varnothing ,\quad \frac{N+m}{p}\in (s_1,s_2+2). \end{aligned}$$

Then, $T(\cdot )$ has maximal regularity on $L^p({\mathbb {R}}^N, d\mu _m)$.

The following remark follows by combining the previous corollary with Proposition 3.5.

Remark 4.16

The Laplacian $\Delta$ generates a semigroup in $L^p(d\mu _m)$ if and only if $-N<m<N(p-1)$, that is when $|x|^m \in A_p$. In such a case it has maximal regularity.