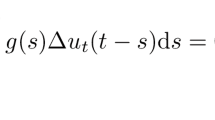Abstract
We consider the Moore–Gibson–Thompson equation with memory of type II
where A is a strictly positive selfadjoint linear operator (bounded or unbounded) and \(\alpha ,\beta ,\gamma >0\) satisfy the relation \(\gamma \le \alpha \beta \). First, we prove well-posedness of finite energy solutions, without requiring any restriction on the total mass \(\varrho \) of g. This extends previous results in the literature, where such a restriction was imposed. Second, we address an open question within the context of longtime behavior of solutions. We show that an “overdamping” in the memory term can destabilize the originally stable dynamics. In fact, it is always possible to find memory kernels g, complying with the usual mass restriction \(\varrho <\beta \), such that the equation admits solutions with energy growing exponentially fast, even in the regime \(\gamma < \alpha \beta \) where the corresponding model without memory is exponentially stable. In particular, this provides an answer to a question recently raised in the literature.
Similar content being viewed by others
References
M.O. Alves, A.H. Caixeta, M.A. Jorge Silva and J.H. Rodrigues, Moore-Gibson-Thompson equation with memory in a history framework: a semigroup approach, Z. Angew. Math. Phys. 69 (2018), n.106.
C.M. Dafermos, Asymptotic stability in viscoelasticity, Arch. Rational Mech. Anal. 37 (1970), 554–569.
F. Dell’Oro, I. Lasiecka and V. Pata, The Moore-Gibson-Thompson equation with memory in the critical case, J. Differential Equations 261, (2016), 4188–4222.
F. Dell’Oro and V. Pata, On the Moore-Gibson-Thompson equation and its relation to linear viscoelasticity., Appl. Math. Optim. 76 (2017), 641–655.
F. Dell’Oro and V. Pata, On a fourth-order equation of Moore-Gibson-Thompson type, Milan J. Math. 85 (2017), 215–234.
M. Fabrizio and S. Polidoro Asymptotic decay for some differential systems with fading memory, Appl. Anal. 81 (2002), 1245–1264.
P. Jordan, Second-sound phenomena in inviscid, thermally relaxing gases, Discrete Contin. Dyn. Syst. Ser. B 19 (2014), 2189–2205.
P. Jordan, Private communication.
B. Kaltenbacher, Mathematics of nonlinear acoustics, Evol. Equ. Control Theory, 4 (2015), 447–491.
B. Kaltenbacher, I. Lasiecka and R. Marchand, Wellposedness and exponential decay rates for the Moore-Gibson-Thompson equation arising in high intensity ultrasound, Control Cybernet. 40 (2011), 971–988.
B. Kaltenbacher, I. Lasiecka and M.K. Pospieszalska, Well-posedness and exponential decay of the energy in the nonlinear Jordan-Moore-Gibson-Thompson equation arising in high intensity ultrasound, Math. Models Methods Appl. Sci. 22 (2012), no. 11, 1250035, 34 pp.
I. Lasiecka, Global solvability of Moore-Gibson-Thompson equation with memory arising in nonlinear acoustics, J. Evol. Equ. 17 (2017), 411-441.
I. Lasiecka and X. Wang, Moore-Gibson-Thompson equation with memory, part II: General decay of energy, J. Differential Equations 259 (2015), 7610–7635.
I. Lasiecka and X. Wang, Moore-Gibson-Thompson equation with memory, part I: Exponential decay of energy, Z. Angew. Math. Phys. 67 (2016), n.17.
G. Lebon and A. Cloot, Propagation of ultrasonic sound waves in dissipative dilute gases and extended irreversible thermodynamics, Wave Motion 11 (1989), 23–32.
R. Marchand, T. McDevitt and R. Triggiani, An abstract semigroup approach to the third-order Moore-Gibson-Thompson partial differential equation arising in high-intensity ultrasound: structural decomposition, spectral analysis, exponential stability, Math. Methods Appl. Sci. 35 (2012), 1896–1929.
F.K. Moore and W.E. Gibson, Propagation of weak disturbances in a gas subject to relaxation effects, J. Aero/Space Sci. 27 (1960), 117–127.
J.E. Muñoz Rivera, Asymptotic behaviour in linear viscoelasticity, Quart. Appl. Math. 52 (1994), 629–648.
K. Naugolnykh and L. Ostrovsky, Nonlinear wave processes in acoustics, Cambridge University Press, Cambridge, 1998.
V. Nikolić and B. Kaltenbacher, Sensitivity analysis for shape optimization of a focusing acoustic lens in lithotripsy, Appl. Math. Optim. 76 (2017), 261–301.
L. Pandolfi Controllability of isotropic viscoelastic bodies of Maxwell-Boltzmann type, ESAIM Control Optim. Calc. Var. 23 (2017), 1649–1666.
V. Pata, Stability and exponential stability in linear viscoelasticity, Milan J. Math. 77 (2009), 333–360.
Professor Stokes, An examination of the possible effect of the radiation of heat on the propagation of sound, Philos. Mag. Series 4 1 (1851), 305–317.
P.A. Thompson, Compressible-fluid dynamics, McGraw-Hill, New York, 1972.
Acknowledgements
The authors would like to thank Monica Conti for fruitful discussion. They also thank the anonymous referee for useful comments and remarks.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Dell’Oro, F., Lasiecka, I. & Pata, V. A note on the Moore–Gibson–Thompson equation with memory of type II. J. Evol. Equ. 20, 1251–1268 (2020). https://doi.org/10.1007/s00028-019-00554-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00028-019-00554-0