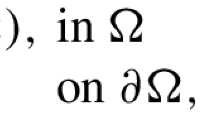Abstract
In this paper, we deal with a class of semilinear parabolic problems related to a Hardy inequality with singular weight at the boundary.
More precisely, we consider the problem
where Ω is a bounded regular domain of \({\mathbbm{R}^N}\), \({d(x)=\text{dist}(x,\partial\Omega)}\), \({p > 0}\), and \({\lambda > 0}\) is a positive constant.
We prove that
-
1.
If \({0 < p < 1}\), then (P) has no positive very weak solution.
-
2.
If \({p=1}\), then (P) has a positive very weak solution under additional hypotheses on \({\lambda}\) and \({u_0}\).
-
3.
If \({p > 1}\), then, for all \({\lambda > 0}\), the problem (P) has a positive very weak solution under suitable hypothesis on \({u_0}\).
Moreover, we consider also the concave–convex-related case.
Similar content being viewed by others
References
B. Abdellaoui, K. Biroud, J. Davila and F. Mahmoudi, Nonlinear elliptic problem related to the Hardy inequality with singular term at the boundary. Commun. Contemp. Math. 17 (2015), no. 3, 1450033.
Abdellaoui B., Peral I., Primo A.: Influence of the Hardy potential in a semilinear heat equation, Proc. Roy. Soc. Edinburgh Sect. A 139, no. 5, 897–926 (2009)
A. Attar, S. Merchan, I. Peral, A remark on existence of semilinear heat equation involving a Hardy–Leray potential. J. Evol. Equ. 15 (2015), no. 1, 239–250.
Baras P., Goldstein J.: The heat equation with a singular potential. Trans. Amer. Math. Soc. 294, 121–139 (1984)
Barbatis G., Filippas S., Tertikas A.: A unified approach to improved \({L^p}\) Hardy inequalities with best constants. Trans. A.M.S. 356(6), 2169–2196 (2003)
Brezis H., Cabré X.: Some simple nonlinear PDE’s without solution. Boll. Unione. Mat. Ital. Sez. B 8, 223–262 (1998)
Brezis H., Kamin S.: Sublinear elliptic equations in \({\mathbbm{R}^N}\). Manuscripta Math. 74, 87–106 (1992)
H. Brezis, M. Marcus, Hardy’s inequalities revisited. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 25 (1997), no. 1–2, 217–237 (1998).
Cabré X., Martel Y.: Existence versus explosion instantanée pour des équations de la chaleur linéaires avec potentiel singulier. C. R. Acad. Sci. Paris Sér. I Math. 329, no. 11, 973–978 (1999)
Cazenave T., Dickstein F., Escobedo M.: A semilinear heat equation with concave–convex nonlinearity. Rendiconti di Matematica, Serie VII 19, 211–242 (1999)
Dávila J., Peral I.: Nonlinear elliptic problems with a singular weight on the boundary. Calc. Var. Partial Differential Equations, 41, no. 3–4, 567–586 (2011)
Garcia-Azorero J., Peral I.: Hardy Inequalities and Some Critical Elliptic and Parabolic Problems. J. Differential Equations, 144(1), 441–476 (1998)
M. Ghergu, V. Radulescu, Singular Elliptic Problems. Bifurcation and Asymptotic Analysis. Oxford Lecture Series in Mathematics and Its Applications, vol. 37, The Clarendon Press, Oxford University Press, (2008).
M. Marcus M, V.J. Mizel, Y. Pinchover, On the best constant for Hardy’s inequality in \({\mathbbm{R}^N}\). Trans. Amer. Math. Soc. 350(1998) 3237–3255
Matskewich T., Sobolevskii P.E.: The best possible constant in generalized Hardy’s inequality for convex domain in \({\mathbbm{R}^N}\). Nonlinear Anal, Theory, Methods and Appl. Vol. 29, 1601–1610 (1997)
Prignet A.: Existence and uniqueness of entropy solution of parabolic problems with \({L^1}\) data. Nonlinear Anal. T.M.A. 28, no. 12, 1943–1954 (1997)
I. Shafrir, Asymptotic behaviour of minimizing sequences for Hardy inequality. Commun. Contemp. Math. no. 2 (2000), 151–189.
A. Tertikas, L. Moschini, S. Filippas, Sharp Two Sided Heat Kernel Estimates for Critical Schrödinger Operators on Bounded Domains. Commun. Math. Phys. (2007), 237–281.
Yvan Martel, Complete blow up and global behaviour of solution of \({u_t-\Delta u=g(u)}\). Ann. Inst. Henri Poincaré, (15) 6 (1998), 687–723.
Author information
Authors and Affiliations
Corresponding author
Additional information
Work partially supported by Project MTM2010-18128, MINECO, Spain.
B. Abdellaoui is also partially supported by a Grant from the ICTP centre of Italy.
Rights and permissions
About this article
Cite this article
Abdellaoui, B., Biroud, K. & Primo, A. A semilinear parabolic problem with singular term at the boundary. J. Evol. Equ. 16, 131–153 (2016). https://doi.org/10.1007/s00028-015-0295-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00028-015-0295-1