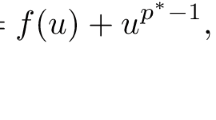Abstract
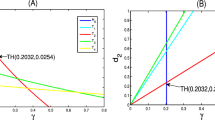
In this paper, we investigate the continuity with respect to the diffusion parameter \({\epsilon}\) of the asymptotic states of an one-dimensional p-Laplacian problem which is a nonlinear version of the well-known Chafee–Infante problem. We obtain the upper semicontinuity at any value \({\epsilon > 0}\) and exhibit cases where the lower semicontinuity of the set of equilibria with respect to the diffusion is always true. Finally, we study a particular case where the lower semicontinuity of the equilibrium set occurs for almost every \({\epsilon > 0}\) but fails when \({\epsilon}\) belongs to the bifurcation sequence. As a consequence, we show that the attractor cannot be continuous at these points.
Similar content being viewed by others
References
A. V. Babin and M. I. Vishik, Attractors of Evolution Equations, North Holland, Amsterdam, 1992.
Babin A.V., Vishik M.I.: Unstable invariant sets of semigroups of nonlinear operators and their perturbations. Russian Mathematical Surveys 41, 1–41 (1986)
Bruschi S.M., Gentile C.B., Primo M. R.T.: Continuity properties on p for p-Laplacian parabolic problems. Nonlinear Analysis 72, 1580–1588 (2010)
S. M. Bruschi, C. B. Gentile and M. R. T. Primo, Upper semicontinuity of attractors and continuity of equilibrium sets of a parabolic problem with a degenerate p-Laplacian, preprint.
Caraballo T., Crauel H., Langa J. A., Robinson J.C.: The effect of noise on the Chafee–Infante equation: a nonlinear case study. Proceedings of the American Mathematical Society 135, 373–382 (2007)
A. N. Carvalho, J. A. Langa and J. C. Robinson (Editors), Asymptotic Dynamics of Non-autonomous Systems, Discrete and Continuous Dynamical Systems - Series B, Special issue on the asymptotic dynamics of non-autonomous systems, 20 (3) (2015), AIMS.
Carvalho A.N., Piskarev S.A.: A general approximation scheme for attractors of abstract parabolic problems. Numerical functional analysis and optimization 27, 785–829 (2006)
Carvalho A.N., Hines G.: Lower semicontinuity of attractors for gradient systems. Dynamic Systems and Applications 9, 37–50 (2000)
Chafee N., Infante E.F.: A bifurcation problem for a nonlinear partial differential equation of parabolic type. Bulletin of the American Mathematical Society 4, 17–37 (1974)
V. V. Chepyzhov and M. I. Vishik, Attractors for equations of mathematical physics, Colloquium Publication 49, American Mathematical Society, Providence, RI, (2002).
P. Constantin, C. Foias, B. Nicolaenko and R. Temam, Integral Manifolds and Inertial Manifolds for Dissipative Partial Differential Equations, Applied Mathematical Sciences, vol 70, Springer-Verlag, New York, 1989.
Elliott C.M., Kostin I.N.: Lower semicontinuity of a non-hyperbolic attractor for the viscous Cahn-Hilliard equation. Nonlinearity 9, 687–702 (1996)
Gentile C.B., Bruschi S.M.: Lap number properties for p-Laplacian problems investigated by Lyapunov methods. Nonlinear Analysis 66, 1005–1015 (2007)
J. K. Hale, Asymptotic behavior of dissipative systems, American Mathematical Society, Providence, RI, 1988.
Hale J.K., Raugel G.: Lower semicontinuity of attractors of gradient systems and applications. Annali di Matematica Pura ed Applicata 154, 281–326 (1989)
D. Henry, Geometric theory of semilinear parabolic equations, Lecture notes in mathematics, vol 840. Springer-Verlag, Berlin Heidelberg New York, 1981.
Li D., Kloeden P.E.: Equi-attraction and the continuous dependence of attractors on parameters. Glasgow Mathematical Journal 46, 131–141 (2004)
Kostin I.N.: Lower semicontinuity of a non-hyperbolic attractor. J. London Math. Soc. 52(2), 568–582 (1995)
A. M. Stuart and A. R. Humphries, Dynamical systems and numerical analysis, Cambridge University Press, Cambridge, 1996.
Takeuchi S., Yamada Y.: Asymptotic properties of a reaction-diffusion equation with degenerate p-Laplacian. Nonlinear Analysis, 42, 41–61 (2000)
R. Temam, Infinite-dimensional dynamical systems in mechanics and physics, Springer-Verlag, New York, 1988.
Author information
Authors and Affiliations
Corresponding author
Additional information
A. C. Pereira was partially supported by CAPES (Brazil).
O. H. Miyagaki was partially supported by CNPq (Brazil).
Rights and permissions
About this article
Cite this article
Pereira, A.C., Gentile Moussa, C.B. & Miyagaki, O.H. An example of noncontinuous attractors. J. Evol. Equ. 15, 979–1000 (2015). https://doi.org/10.1007/s00028-015-0289-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00028-015-0289-z