Skip to main content
SpringerLink
Log in

A Proof of the \(\frac{n!}{2}\) Conjecture for Hook Shapes

  • Published:
Annals of Combinatorics Aims and scope Submit manuscript

Abstract

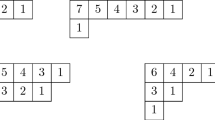
A well-known representation-theoretic model for the transformed Macdonald polynomial \({\widetilde{H}}_\mu (Z;t,q)\), where \(\mu \) is an integer partition, is given by the Garsia–Haiman module \({\mathcal {H}}_\mu \). We study the \(\frac{n!}{k}\) conjecture of Bergeron and Garsia, which concerns the behavior of certain k-tuples of Garsia–Haiman modules under intersection. In the special case that \(\mu \) has hook shape, we use a basis for \({\mathcal {H}}_\mu \) due to Adin, Remmel, and Roichman to resolve the \(\frac{n!}{2}\) conjecture by constructing an explicit basis for the intersection of two Garsia–Haiman modules.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Macdonald, I.G.: A new class of symmetric functions. Actes du 20\(\,^{\circ }\) Séminaire Lotharingien, 131–171 (1988)

  2. Haiman, M.: Hilbert schemes, polygraphs, and the Macdonald positivity conjecture. J. Amer. Math. Soc. 14(4), 941–1006 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bergeron, F., Garsia, A.M.: Science Fiction and Macdonald’s Polynomials. In: Algebraic Methods and \(q\)-special Functions (Montréal, QC, 1996), vol.22, pp. 1–52 (1999)

  4. Adin, R.M., Remmel, J.B., Roichman, Y.: The combinatorics of the Garsia-Haiman modules for hook shapes. Electron. J. Combin. 15(1), 38–42 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  5. Haglund, J., Haiman, M., Loehr, N.: A combinatorial formula for Macdonald polynomials. J. Amer. Math. Soc. 18(3), 735–761 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  6. Haglund, J.: A combinatorial model for the Macdonald polynomials. Proc. Natl. Acad. Sci. USA 101(46), 16127–16131 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  7. Garsia, A.M., Haiman, M.: A graded representation model for Macdonald’s polynomials. Proc. Nat. Acad. Sci. U.S.A. 90(8), 3607–3610 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  8. Haiman, M.: Macdonald polynomials and geometry. New perspectives in algebraic combinatorics (Berkeley, CA, 1996–97) 38(207–254) (1999)

  9. Allen, E.E.: Bitableaux bases for some Garsia-Haiman modules and other related modules. Electron. J. Combin. 9(1), 36–59 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  10. Assaf, S., Garsia, A.: A Kicking Basis for the Two Column Garsia-Haiman Modules. In: 21st International Conference on Formal Power Series and Algebraic Combinatorics (FPSAC 2009), pp. 103–114. Assoc. Discrete Math. Theor. Comput. Sci., Nancy (2009)

  11. Aval, J.-C.: Monomial bases related to the \(n!\) conjecture. Discrete Math. 224(1-3), 15–35 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  12. Garsia, A.M., Haiman, M.: Some natural bigraded \(S_n\)-modules and \(q,t\)-Kostka coefficients. Electron. J. Combin. 3(2), 24–60 (1996)

  13. Stembridge, J.R.: Some particular entries of the two-parameter Kostka matrix. Proc. Amer. Math. Soc. 121(2), 367–373 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  14. Garsia, A.M., Haiman, M.: Factorizations of Pieri rules for Macdonald polynomials. Discrete Math. 139(1-3), 219–256 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  15. Garsia, A.M., Haiman, M.: Orbit harmonics and graded representations

  16. Bergeron, F., Hamel, S.: Intersection of modules related to Macdonald’s polynomials. Discrete Math. 217(1-3), 51–64 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  17. Foata, Dominique: On the Netto inversion number of a sequence. Proc. Amer. Math. Soc. 19, 236–240 (1968)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Southern California, 3620 S Vermont Avenue, Los Angeles, CA, 90089, USA

    Sam Armon

Authors
  1. Sam Armon
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sam Armon.

Ethics declarations

Conflict of interest

On behalf of all the authors, the corresponding author states that there is no conflict of interest.

Data sharing

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Additional information

Communicated by Alexander Yong.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Armon, S. A Proof of the \(\frac{n!}{2}\) Conjecture for Hook Shapes. Ann. Comb. 27, 819–832 (2023). https://doi.org/10.1007/s00026-022-00613-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00026-022-00613-3

Keywords

Search

Navigation