Total Nonnegativity and Induced Sign Characters of the Hecke Algebra

Abstract

Let ${\mathfrak {S}}_{[i,j]}$ be the subgroup of the symmetric group ${\mathfrak {S}}_n$ generated by adjacent transpositions $(i,i+1), \dotsc , (j-1,j)$, assuming $1 \le i < j \le n$. We give a combinatorial rule for evaluating induced sign characters of the type A Hecke algebra $H_n(q)$ at all elements of the form $\sum _{w \in {\mathfrak {S}}_{[i,j]}} T_w$ and at all products of such elements. This includes evaluation at some elements $C'_w(q)$ of the Kazhdan–Lusztig basis.

1 Introduction

Concepts of total nonnegativity, first explored by Gantmacher and Krein [9] have found their way into many areas of mathematics, including the study of polynomials $p(x_{1,1},\dotsc ,x_{n,n})$ satisfying $p(a_{1,1}, \dotsc , a_{n,n}) \ge 0$ for every totally nonnegative $n \times n$ matrix $A = (a_{i,j})$. We call these totally nonnegative (TNN) polynomials. In particular, work of Lusztig [17] implies that in ${\mathbb {Z}}[x]:={\mathbb {Z}}[x_{1,1},\dotsc ,x_{n,n}]$, certain elements which are related to the dual canonical basis of the quantum group ${{\mathcal {O}}}_q(SL_n ({\mathbb {C}}))$ are TNN polynomials.

In practice, it is sometimes possible to use cluster algebras [8] and a computer to demonstrate that a polynomial is TNN by expressing it as a subtraction-free rational expression in matrix minors. On the other hand, no simple characterization of TNN polynomials is known. To improve our understanding of TNN polynomials, one might begin by investigating the immanant subspace $\mathrm {span}_{{\mathbb {Z}}} \{ x_{1,w_1} \,\cdots {x}_{n,w_n} \,|\, w \in {\mathfrak {S}}_n\}$ of ${\mathbb {Z}}[x]$, especially the generating functions

$$\begin{aligned} \mathrm {Imm}_{\theta }(x) :=\sum _{w \in {\mathfrak {S}}_n} \theta (w) x_{1,w_1} \,\cdots {x}_{n,w_n} \end{aligned}$$

(1.1)

for class functions $\theta : {\mathfrak {S}}_n\rightarrow {\mathbb {Z}}$. Or, since the Hecke algebra $H_n(q)$ satisfies $H_n(1) \cong {\mathbb {Z}}[{\mathfrak {S}}_n]$, and since some results relate total nonnegativity to $H_n(q)$-traces $\theta _q: H_n(q)\rightarrow {\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$, one might investigate these.

In particular, let $\{ {\widetilde{C}}_{w}(q) \,|\, w \in {\mathfrak {S}}_n\}$ be the (modified, signless) Kazhdan–Lusztig basis of $H_n(q)$, and let $\{ {\widetilde{C}}_{w}(1) \,|\, w \in {\mathfrak {S}}_n\}$ be the corresponding basis of ${\mathbb {Z}}[{\mathfrak {S}}_n]$. (See §2 for a brief introduction.) For $1 \le a < b \le n$, let $s_{[a,b]} \in {\mathfrak {S}}_n$ be the reversal whose one-line notation is $1 \cdots (a-1) b (b-1) \cdots (a+1) a (a+2) \cdots n$. Stembridge [21, Thm. 2.1] showed that for any linear function $\theta : {\mathbb {Z}}[{\mathfrak {S}}_n]\rightarrow {\mathbb {Z}}$, the immanant $\mathrm {Imm}_{\theta }(x)$ is TNN if for all sequences $J_1, \dotsc , J_m$ of subintervals of $[n] :=\{1, \dotsc , n\}$, we have

$$\begin{aligned} \theta ({\widetilde{C}}_{s_{J_1}\,}(1) \cdots {\widetilde{C}}_{s_{J_m}\,}(1)) \ge 0. \end{aligned}$$

(1.2)

Furthermore, by Lindström’s Lemma [16] and its converse [4, 6], a combinatorial interpretation of the above expression would immediately yield a combinatorial interpretation of the number $\mathrm {Imm}_{\theta }(A)$ for A a TNN matrix. Now if a linear function $\theta _q: H_n(q)\rightarrow {\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$ specializes at $q^{\frac{1}{2}} = 1$ to $\theta$, then (1.2) is clearly a consequence of the condition

$$\begin{aligned} \theta _q({\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)) \in {\mathbb {N}}[q], \end{aligned}$$

(1.3)

and a combinatorial interpretation of coefficients of the above polynomial would yield combinatorial interpretations of the earlier expressions. Haiman [10, Appendix] observed that (1.3) in turn follows from the condition that for all $w \in {\mathfrak {S}}_n$, we have

$$\begin{aligned} \theta _q({\widetilde{C}}_{w}(q)) \in {\mathbb {N}}[q] \end{aligned}$$

(1.4)

since results in [1, 20] imply that any product of Kazhdan–Lusztig basis elements belongs to $\mathrm {span}_{{\mathbb {N}}[q]}\{ {\widetilde{C}}_{w}(q) \,|\, w \in {\mathfrak {S}}_n\}$. On the other hand, it is not clear that the coefficients in the resulting linear combination would lead to a combinatorial interpretation of the expression in (1.3).

Stembridge [21, Cor. 3.3] proved that for each irreducible ${\mathfrak {S}}_n$-character $\chi ^\lambda$, the evaluation (1.2) belongs to ${\mathbb {N}}$. Haiman [10, Lem. 1.1] proved that for each corresponding irreducible $H_n(q)$-character $\chi _q^\lambda$, the evaluation (1.4) belongs to ${\mathbb {N}}[q]$. They conjectured the same statements [22, Conj. 2.1], [10, Conj. 2.1] to hold for functions $\phi ^\lambda$, $\phi _q^\lambda$, called monomial traces of ${\mathfrak {S}}_n$ and $H_n(q)$, respectively. These traces are related to irreducible characters by the inverse Kostka numbers,

$$\begin{aligned} \phi ^\lambda = \sum _{\mu \vdash n} K^{-1}_{\lambda ,\mu } \chi ^\mu , \qquad \phi _q^\lambda = \sum _{\mu \vdash n} K^{-1}_{\lambda ,\mu } \chi _q^\mu , \end{aligned}$$

where $\mu \vdash n$ denotes that $\mu$ varies over all partitions of n. The sets $\{ \chi ^\lambda \,|\, \lambda \vdash n \}$, $\{ \phi ^\lambda \,|\, \lambda \vdash n \}$ form bases of the space of ${\mathfrak {S}}_n$-class functions, and the sets $\{ \chi _q^\lambda \,|\, \lambda \vdash n \}$, $\{ \phi _q^\lambda \,|\, \lambda \vdash n \}$ form bases of the $H_n(q)$-trace space. (See, e.g., [3, §A3.9], [22, §1].)

None of these results or conjectures included a combinatorial interpretation. For the purposes of understanding TNN polynomials of the form (1.1), it would be desirable to solve the following problem.

Problem 1.1

Give combinatorial interpretations of all of the expressions in (1.3) when $\theta _q$ varies over all elements of any basis of the $H_n(q)$-trace space.

So far, only some special cases have such interpretations. In the case that w avoids the patterns $3412$ and $4231$, the Kazhdan–Lusztig basis element ${\widetilde{C}}_{w}(q)$ is closely related to a product of the form appearing in (1.3). Combinatorial interpretations of the corresponding expressions (1.3) and (1.4) were given in [5] for $\theta _q \in \{\chi _q^\lambda \,|\, \lambda \vdash n\}$, and for $\theta _q$ belonging to several other bases of the $H_n(q)$-trace space, including the basis $\{ \epsilon _q^\lambda \,|\, \lambda \vdash n \}$ of induced sign characters. Combinatorial interpretations for $\theta _q = \phi _q^\lambda$ were given only when $\lambda$ has at most two parts [5, Thm. 10.3], or when $\lambda$ has rectangular shape and $q=1$ [22, Thm. 2.8].

In the case that all reversals $s_{J_1},\dotsc ,s_{J_m}$ in (1.3) are adjacent transpositions, combinatorial interpretations of

$$\begin{aligned} \epsilon _q^\lambda ({\widetilde{C}}_{s_{[j_1,j_1+1]}\,}(q) \cdots {\widetilde{C}}_{s_{[j_m,j_m+1]}\,}(q)) \end{aligned}$$

for all $\lambda \vdash n$ were given in [11, Thm. 5.4], nearly solving Problem 1.1. To complete the solution of Problem 1.1, we generalize [11, Thm. 5.4] to interpret all evaluations of the form

$$\begin{aligned} \epsilon _q^\lambda ({\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)), \end{aligned}$$

(1.5)

where the intervals $J_1, \dotsc , J_m \subseteq [n]$ have arbitrary cardinality. The justification of our solution closely follows the steps used in [11, §3–5], with definitions and propositions generalized as necessary.

In Sect. 2, we discuss the symmetric group algebra ${\mathbb {Z}}[{\mathfrak {S}}_n]$, the Hecke algebra $H_n(q)$, and a noncommutative q-analog ${\mathcal {A}}= {\mathcal {A}}(n,q)$ of ${\mathbb {Z}}[x]$ known as the quantum matrix bialgebra. The q-analogs $\mathrm {Imm}_{\theta _q}(x)$ of immanants (1.1) belong to a q-analog ${\mathcal {A}}_{[n],[n]}\subset {\mathcal {A}}$ of the immanant subspace of ${\mathbb {Z}}[x]$, and $\mathrm {Imm}_{\epsilon _q^\lambda }(x)$ has a natural expression in terms of certain monomials which we write as $\{x^{u,w} \,|\, u, w \in {\mathfrak {S}}_n\}$. In Sect. 3, we consider elements of the form $\smash {{\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)} \in H_n(q)$, and we associate with each a planar network G, a related matrix B, and a linear map $\sigma _B: {\mathcal {A}}_{[n],[n]}\rightarrow {\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$. In Sect. 4, we interpret $\sigma _B(x^{u,w}) \in {\mathbb {N}}[q]$ for each pair $u,w \in {\mathfrak {S}}_n$ in terms of statistics on families of source-to-sink paths in G and on tableaux filled with such paths. In Sect. 5, we show that for each $H_n(q)$-trace $\theta _q$ and its generating function $\mathrm {Imm}_{\theta _q}(x)$, we have the identity

$$\begin{aligned} \theta _q({\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)) = \sigma _B(\mathrm {Imm}_{\theta _q}(x)). \end{aligned}$$

(1.6)

This identity leads to our main result in Sect. 6, where we use path families, tableaux, and $\mathrm {Imm}_{\epsilon _q^\lambda }(x)$ to combinatorially evaluate the expressions (1.5).

2 Algebraic Background

Define the symmetric group algebra ${\mathbb {Z}}[{\mathfrak {S}}_n]$ and the (type A Iwahori-)-Hecke algebra $H_n(q)$ to be the algebras with multiplicative identity elements e and $T_e$, respectively, generated over ${\mathbb {Z}}$ and ${\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$ by elements $s_1,\dotsc , s_{n-1}$ and $T_{s_1},\dotsc , T_{s_{n-1}}$, subject to the relations

(2.1)

Analogous to the natural basis $\{ w \,|\, w \in {\mathfrak {S}}_n\}$ of ${\mathbb {Z}}[{\mathfrak {S}}_n]$ is the natural basis $\{ T_w \,|\, w \in {\mathfrak {S}}_n\}$ of $H_n(q)$, where we define $T_w = T_{s_{i_1}} \,\cdots T_{s_{i_\ell }}$ whenever $s_{i_1} \,\cdots s_{i_\ell }$ is a reduced (short as possible) expression for w in ${\mathfrak {S}}_n$. We call $\ell$ the length of w and write $\ell = \ell (w)$. We define the one-line notation $w_1 \cdots w_n$ of $w \in {\mathfrak {S}}_n$ by letting any expression for w act on the word $1 \cdots n$, where each generator $s_j = s_{[j,j+1]}$ acts on an n-letter word by swapping the letters in positions j and $j+1$, i.e., $s_j \circ v_1 \cdots v_n = v_1 \cdots v_{j-1} v_{j+1} v_j v_{j+2} \cdots v_n$. It is easy to show that $\ell (w)$ is equal to $\textsc {inv}(w)$, the number of inversions in the one-line notation $w_1 \cdots w_n$ of w. Specializing at $q^{\frac{1}{2}} = 1$, we have $T_v \mapsto v$ and $H_n(1) \cong {\mathbb {Z}}[{\mathfrak {S}}_n]$.

A semilinear involution on $H_n(q)$, known as the bar involution,

$$\begin{aligned} \sum _{w \in {\mathfrak {S}}_n} a_w T_w \mapsto \overline{\sum _{w \in {\mathfrak {S}}_n} a_w T_w} = \sum _{w \in {\mathfrak {S}}_n} \overline{a_w}\, \overline{T_w}, \end{aligned}$$

is defined by

$$\begin{aligned} \overline{q^{\frac{1}{2}}} = q^{\,\bar{\,}\frac{1}{2}}, \qquad \overline{T_w} = (T_{w^{-1}})^{-1}. \end{aligned}$$

Kazhdan and Lusztig showed [13] that $H_n(q)$ has a unique basis $\{ C'_w(q) \,|\, w \in {\mathfrak {S}}_n\}$ satisfying

$$\begin{aligned} \overline{C'_w(q)} = C'_w(q); \qquad C'_w(q) \in q^{\,\bar{\,}\frac{\ell (w)}{2}} T_w + \sum _{v < w} q^{\,\bar{\,}\frac{1}{2}} {\mathbb {Z}}[q^{\,\bar{\,}\frac{1}{2}}] q^{\,\bar{\,}\frac{\ell (v)}{2}} T_v, \end{aligned}$$

where < denotes the Bruhat order. (See [3, §2].) Modifying this basis by ${\widetilde{C}}_{w}(q) :=q^{\frac{\ell (w)}{2}} C'_w(q)$ and expanding in the natural basis, we have

$$\begin{aligned} {\widetilde{C}}_{w}(q) = \sum _{v \le w} P_{v,w}(q) T_v, \end{aligned}$$

(2.2)

where the coefficients $P_{v,w}(q)$ belong to ${\mathbb {N}}[q]$ and are called Kazhdan–Lusztig polynomials. If the one-line notation for w contains no subword matching the pattern 3412 or 4231 (e.g., if w is a reversal), then the Kazhdan–Lusztig polynomials in (2.2) are identically 1 [15].

For any subinterval $J = [a,b]$ of $[n] :=\{1, \dotsc , n\}$, define ${\mathfrak {S}}_{J}$ to be the subgroup of ${\mathfrak {S}}_n$ generated by $\{s_a, \dotsc , s_{b-1}\}$. The longest element of ${\mathfrak {S}}_{J} \cong {\mathfrak {S}}_{b-a+1}$ is the reversal $s_J :=s_{[a,b]}$. Define ${\mathfrak {S}}_-^{J}$ to be the set of unique minimum length representatives of left cosets $w {\mathfrak {S}}_{J}$, i.e., the elements $w \in {\mathfrak {S}}_n$ satisfying $ws_i > w$ for all $i \in [a,b-1]$. A bijection of ${\mathfrak {S}}_n$ with ${\mathfrak {S}}_-^{J} \times {\mathfrak {S}}_{J}$ is given by the fact that each element $w \in {\mathfrak {S}}_n$ factors uniquely as

$$\begin{aligned} w = w_- w^*, \end{aligned}$$

(2.3)

with $(w_-,w^*) \in {\mathfrak {S}}_-^{J} \times {\mathfrak {S}}_{J}$ and $\ell (w_-) + \ell (w^*) = \ell (w)$. This factorization satisfies the identity

$$\begin{aligned} T_w {\widetilde{C}}_{s_J \,}(q) = T_{w_-} T_{w^*} {\widetilde{C}}_{s_J \,}(q) = q^{\ell (w^*)} T_{w_-} {\widetilde{C}}_{s_J \,}(q). \end{aligned}$$

(2.4)

A similar factorization result employs the set ${\mathfrak {S}}_{J}^-$ of minimum length representatives of right cosets ${\mathfrak {S}}_{J} w$, and defines a bijection from ${\mathfrak {S}}_n$ to ${\mathfrak {S}}_{J} \times {\mathfrak {S}}_{J}^-$. (See, e.g., [3, Prop. 2.4.4, Cor. 2.4.5], [10, Eq. 8.9].)

For any partition $\lambda = (\lambda _1, \dotsc , \lambda _r) \vdash n$, the subgroup

$$\begin{aligned} {\mathfrak {S}}_{\lambda } :={\mathfrak {S}}_{[1,\lambda _1]} \times {\mathfrak {S}}_{[\lambda _1 + 1,\lambda _1 + \lambda _2]} \times \cdots \times {\mathfrak {S}}_{[n-\lambda _r+1,n]} \cong {\mathfrak {S}}_{\lambda _1} \times {\mathfrak {S}}_{\lambda _2} \times \cdots \times {\mathfrak {S}}_{\lambda _r} \end{aligned}$$

of ${\mathfrak {S}}_n$ generated by

$$\begin{aligned} \{ s_1, \dotsc , s_{n-1} \} \smallsetminus \{ s_{\lambda _1}, s_{\lambda _1 + \lambda _2}, s_{\lambda _1 + \lambda _2 + \lambda _3}, \dotsc , s_{n-\lambda _r} \} \end{aligned}$$

(2.5)

is called the Young subgroup indexed by $\lambda$. Define $H_\lambda (q)$ to be the subalgebra of $H_n(q)$ generated by the corresponding elements $T_{s_i}$. Define ${\mathfrak {S}}_\lambda ^{-}$ to be the set of minimum length representatives of right cosets ${\mathfrak {S}}_{\lambda }u$, i.e., the elements $u \in {\mathfrak {S}}_n$ satisfying $s_iu > u$ for all $s_i$ in the set (2.5).

Equivalently, ${\mathfrak {S}}_\lambda ^{-}$ consists of all $u \in {\mathfrak {S}}_n$ whose one-line notations are concatenations of r increasing subwords

$$\begin{aligned} u_1 \cdots u_{\lambda _1}, \quad u_{\lambda _1 +1} \cdots u_{\lambda _1 + \lambda _2}, \quad u_{\lambda _1 + \lambda _2 + 1} \cdots u_{\lambda _1 + \lambda _2 + \lambda _3}, \quad \dotsc ,\nonumber \\ \quad u_{n-\lambda _r + 1} \cdots u_n. \end{aligned}$$

(2.6)

The bijections of ${\mathfrak {S}}_n$ with ${\mathfrak {S}}_{J} \times {\mathfrak {S}}_{J}^-$, for $J = [1,\lambda _1], [\lambda _1 + 1, \lambda _1 + \lambda _2], \dotsc , [n-\lambda _r+1,n]$, extend to a bijection of ${\mathfrak {S}}_n$ with ${\mathfrak {S}}_\lambda \times {\mathfrak {S}}_\lambda ^{-}$ and a unique factorization of each element $w \in {\mathfrak {S}}_n$ as

$$\begin{aligned} w = w^\circ w^- \end{aligned}$$

(2.7)

with $(w^\circ , w^-) \in {\mathfrak {S}}_\lambda \times {\mathfrak {S}}_\lambda ^{-}$ and $\ell (w^\circ ) + \ell (w^-) = \ell (w)$. Observe that ${\mathfrak {S}}_{[a,b]}$ is itself a generalization of a Young subgroup corresponding to the composition $1^{a-1}(b-a+1)1^{n-b}$, e.g., the subgroup ${\mathfrak {S}}_{[4,8]}$ of ${\mathfrak {S}}_{10}$ can be written as ${\mathfrak {S}}_{111511}$.

We call a linear function $\theta _q: H_n(q) \rightarrow {\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$ an $H_n(q)$-trace if it satisfies $\theta _q(gh) = \theta _q(hg)$ for all $g, h \in H_n(q)$. Such functions form a free ${\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$-module of rank equal to the number of partitions of n, and include the characters of all finite representations of $H_n(q)$. The specialization at $q^{\frac{1}{2}} = 1$ of a trace is an ${\mathfrak {S}}_n$-class function. Two bases of the module of $H_n(q)$-trace functions are the set of irreducible characters $\{ \chi _q^\lambda \,|\, \lambda \vdash n \}$ and the set of induced sign characters $\{ \epsilon _q^\lambda \,|\, \lambda \vdash n \}$, where

$$\begin{aligned} \epsilon _q^\lambda = \mathrm {sgn}\,\uparrow _{H_\lambda (q)}^{H_n(q)}, \qquad \mathrm {sgn}(T_{s_i}) = -1. \end{aligned}$$

Define the quantum matrix bialgebra ${\mathcal {A}}= {\mathcal {A}}(n,q)$ to be to be the associative algebra with unit 1 generated over ${\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$ by $n^2$ variables $x=(x_{1,1},\dots ,x_{n,n})$, subject to the relations

(2.8)

for all indices $1 \le i < j \le n$ and $1 \le k < \ell \le n$. (See [18].) The counit map $\varepsilon (x_{i,j}) = \delta _{i,j}$, and coproduct map $\Delta (x_{i,j}) = \sum _{k=1}^n x_{i,k} \otimes x_{k,j}$ give ${\mathcal {A}}$ a bialgebra structure. While not a Hopf algebra, ${\mathcal {A}}$ is closely related to the quantum group ${{\mathcal {O}}}_q(SL_n ({\mathbb {C}}))\cong {\mathbb {C}} \otimes {\mathcal {A}}/(\mathrm {det}_q(x)-1)$, where

$$\begin{aligned} \mathrm {det}_q(x) :=\sum _{v \in {\mathfrak {S}}_n} (-q^{\,\bar{\,}\frac{1}{2}})^{\ell (v)} x_{1,v_1} \,\cdots {x}_{n,v_n} \end{aligned}$$

(2.9)

is the ($n \times n$) quantum determinant of the matrix $x = (x_{i,j})$. The antipode map of this Hopf algebra is ${\mathcal {S}} (x_{i,j}) = (-q^{\frac{1}{2}})^{j-i} \mathrm {det}_q(x_{[n]\smallsetminus \{j\}, [n]\smallsetminus \{i\}})$, where $x_{L,M} :=(x_{\ell ,m})_{\ell \in L, m \in M}$, and $\mathrm {det}_q(x_{L,M})$ is defined analogously to (2.9), assuming $|L| = |M|$. Specializing ${\mathcal {A}}$ at $q^{\frac{1}{2}} = 1$, we obtain the commutative ring ${\mathbb {Z}}[x]$.

As a ${\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$-module, ${\mathcal {A}}$ has a natural basis $\{ x_{1,1}^{a_{1,1}} \cdots x_{n,n}^{a_{n,n}} \,|\, a_{1,1}, \dotsc , a_{n,n} \in {\mathbb {N}} \}$ of monomials in which variables appear in lexicographic order, and the relations (2.8) provide an algorithm for expressing any other monomial in terms of this basis. The submodule ${\mathcal {A}}_{[n],[n]}$ spanned by the monomials $\{ x^{u,w} :=x_{u_1,w_1} \cdots x_{u_n,w_n} \mid u,w \in {\mathfrak {S}}_n\}$ has rank n! and natural basis $\{ x^{e,w} \,|\, w \in {\mathfrak {S}}_n\}$. Alternatively, for any fixed u, the set $\{ x^{u,w} \,|\, w \in {\mathfrak {S}}_n\}$ is a basis as well. By (2.8), this basis can be related to the natural basis by repeatedly choosing a generator s satisfying $su < u$ and writing

$$\begin{aligned} x^{u,w} = {\left\{ \begin{array}{ll} x^{su,sw} &{}\quad \text {if }sw > w,\\ x^{su,sw} + (q^{\frac{1}{2}} - q^{\,\bar{\,}\frac{1}{2}})x^{su,w} &{}\quad \text {if }sw < w. \end{array}\right. } \end{aligned}$$

(2.10)

For any linear function $\theta _q: H_n(q)\rightarrow {\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$, we may define the generating function

$$\begin{aligned} \mathrm {Imm}_{\theta _q}(x) :=\sum _{w \in {\mathfrak {S}}_n} q^{\,\bar{\,}\frac{\ell (w)}{2}}\theta _q(T_w) x_{1,w_1} \,\cdots {x}_{n,w_n} \end{aligned}$$

(2.11)

in ${\mathcal {A}}_{[n],[n]}$ which is a q-analog of the generating function (1.1). For example, the generating function for the induced sign character $\epsilon _q^\lambda$ is

$$\begin{aligned} \mathrm {Imm}_{\epsilon _q^\lambda }(x) = \sum _I \mathrm {det}_q(x_{I_1,I_1}) \cdots \mathrm {det}_q(x_{I_r,I_r}), \end{aligned}$$

(2.12)

where the sum is over all ordered set partitions $I = (I_1,\dotsc ,I_r)$ of [n] having type $\lambda$, i.e., satisfying $|I_j| = \lambda _j$ [14, Thm. 5.4]. Fixing an ordered set partition I and expanding the corresponding term on the right-hand side of (2.12), we obtain

$$\begin{aligned} \mathrm {det}_q(x_{I_1,I_1}) \cdots \mathrm {det}_q(x_{I_r,I_r}) = \sum _{y \in {\mathfrak {S}}_\lambda } (-1)^{\ell (y)} q^{\,\bar{\,}\frac{\ell (y)}{2}} x^{u,yu}, \end{aligned}$$

(2.13)

where $u = u(I)$ is the element of ${\mathfrak {S}}_\lambda ^{-}$ whose r increasing subwords (2.6) are the increasing rearrangements of the blocks $I_1, \dotsc , I_r$ of I. As I varies over all ordered set partitions of type $\lambda$, u varies over all elements of ${\mathfrak {S}}_\lambda ^{-}$ and we have

$$\begin{aligned} \mathrm {Imm}_{\epsilon _q^\lambda }(x) = \sum _{u \in {\mathfrak {S}}_\lambda ^{-}} \sum _{y \in {\mathfrak {S}}_\lambda } (-1)^{\ell (y)} q^{\,\bar{\,}\frac{\ell (y)}{2}} x^{u,yu}. \end{aligned}$$

(2.14)

A special case of the induced sign character immanant (2.12) is the generating function for the Hecke algebra sign character $\epsilon _q^n = \chi _q^{1^n}$: the quantum determinant (2.9).

3 Star Networks and the Evaluation Map

To each element of the form $\smash {{\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)} \in H_n(q)$, we associate a planar network G, a related matrix B, and a linear map $\sigma _B: {\mathcal {A}}_{[n],[n]}\rightarrow {\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$. These three objects play crucial roles in the justification of the identity (1.6) in Theorem 5.2, which in turn is necessary for the justification of our main result in Theorem 6.5.

These three definitions are straightforward generalizations of those given in [11, §3.1–3.2] for elements of the form $\smash {{\widetilde{C}}_{s_{i_1}\,}(q) \cdots {\widetilde{C}}_{s_{i_m}\,}(q)} \in H_n(q)$, i.e., where $|J_1| = \cdots = |J_m| = 2$. Other predecessors of the definitions, appearing in [5, §3], [19, §5], pertained to sequences $(J_1, \dotsc , J_m)$ of intervals satisfying the strict “zig-zag” conditions stated in [5, §3], [19, §3].

3.1 The Network G Associated with ${\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)$

To the Kazhdan–Lusztig basis element ${\widetilde{C}}_{s_{[a,b]}\,}(q)$, we associate a (simple, directed, planar) graph $G_{[a,b]}$ on $2n+1$ vertices. For $1 \le a < b \le n$, define $G_{[a,b]}$ as follows.

• (1) On the left is a column of n vertices labeled source 1 $, \dotsc ,$ source n, from bottom to top.

• (2) On the right is a column of n vertices, labeled sink 1 $, \dotsc ,$ sink n, from bottom to top.

• (3) An interior vertex is placed between the sources and sinks.

• (4) For $i = 1, \dotsc , a-1$ and $i = b+1, \dotsc , n$, a directed edge begins at source i and terminates at sink i.

• (5) For $i = a, \dotsc , b$, a directed edge begins at source i and terminates at the interior vertex, and another directed edge begins at the interior vertex and terminates at sink i.

For $a = 1,\dotsc , n$ we define $G_{[a,a]}$ to be the similar directed planar graph on n sources and n sinks with n edges, each from source i to sink i, for $i = 1, \dotsc , n$. Call each of the above graphs a simple star network. In figures we will not explicitly draw vertices or show edge orientations (assumed to be from left to right). For $n = 4$, there are seven simple star networks: $G_{[1,4]}$, $G_{[2,4]}$, $G_{[1,3]}$, $G_{[3,4]}$, $G_{[2,3]}$, $G_{[1,2]}$, $G_{[1,1]} = \cdots = G_{[4,4]}$, respectively,

(3.1)

Define a star network to be the concatenation of finitely many simple star networks. We write $G \circ H$ for concatenation of G and H, formed by identifying sink i of G with source i of H to form an internal vertex, for $i = 1,\dotsc , n$. The sources of $G \circ H$ are those of G, and the sinks of $G \circ H$ are those of H. For example, when $n = 4$ we have

(3.2)

Let $\pi = (\pi _1,\dotsc ,\pi _n)$ be a sequence of source-to-sink paths in a star network G. We call $\pi$ a path family if there exists a permutation $w = w_1 \cdots w_n \in {\mathfrak {S}}_n$ such that $\pi _i$ is a path from source i to sink $w_i$. In this case, we say more specifically that $\pi$ has type w. We say that the path family covers G if it contains every edge exactly once. For example, the stars in the star network $G_{[1,2]} \circ G_{[2,4]}\circ G_{[1,2]}$ (3.2) imply that there are $2 \cdot 6 \cdot 2 = 24$ path families that cover it. Four of these are

(3.3)

The simple star network $G_{[a,b]}$ represents the Kazhdan–Lusztig basis element ${\widetilde{C}}_{s_{[a,b]}\,}(q)$ in the sense that we have

$$\begin{aligned} {\widetilde{C}}_{s_{[a,b]}\,}(q) = \sum _\pi T_{\mathrm {type}(\pi )}, \end{aligned}$$

where the sum is over all path families which cover $G_{[a,b]}$. The concatenation $G_{J_1} \circ \cdots \circ G_{J_m}$ represents the product ${\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)$ in a sense which we will make more precise in Corollary 5.3.

3.2 The Matrix B Associated with ${\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)$

One can enhance any planar network by associating with each edge a weight belonging to some ring R, and by defining the weight of a path to be the product of its edge weights. If R is noncommutative, then one multiplies weights in the order that the corresponding edges appear in the path. For a family $\pi = (\pi _1,\dotsc ,\pi _n)$ of n paths in a planar network, one defines $\mathrm {wgt}(\pi ) = \mathrm {wgt}(\pi _1) \cdots \mathrm {wgt}(\pi _n)$. The (weighted) path matrix $B = B(G) = (b_{i,j})$ of G is defined by letting $b_{i,j}$ be the sum of weights of all paths in G from source i to sink j. Thus the product $b_{1,w_1} \,\cdots {b}_{n,w_n}$ is equal to the sum of weights of all path families of type w in G (covering G or not). It is easy to show that path matrices respect concatenation: $B(G_1 \circ G_2) = B(G_1)B(G_2)$. When R is commutative, a result known as Lindström’s Lemma [12, 16] asserts that for row and column sets I, J with $|I| = |J|$, the minor $\det (B_{I,J})$ is equal to the sum of weights of all nonintersecting path families from sources indexed by I to sinks indexed by J.

Assigning weights to the edges of $G = G_{J_1} \circ \cdots \circ G_{J_m}$ can aid in the evaluation of a linear function $\theta _q: H_n(q)\rightarrow {\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$ at ${\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)$ by relating this evaluation to the generating function (2.11). In particular, let $\{ z_{h,p,k} \,|\, 1 \le p \le r; i_p \le h \le j_p; 1 \le k \le 2 \}$ be indeterminate weights satisfying

$$\begin{aligned} z_{h_2,p_2,k_2} z_{h_1,p_1,k_1} = {\left\{ \begin{array}{ll} z_{h_1,p_1,k_1} z_{h_2,p_2,k_2} &{}\quad \text {if }p_1 \ne p_2,\text { or }k_1 \ne k_2,\\ q^{\frac{1}{2}} z_{h_1,p_1,k_1} z_{h_2,p_2,k_2} &{}\quad \text {if }p_1 = p_2, k_1 = k_2,\text { and }h_1 < h_2. \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.4)

We assign weights to the edges of $G_{J_p} = G_{[i_p,j_p]}$ as follows.

• (1) Assign weight 1 to the $n - j_p + i_p - 1$ edges not incident upon the central vertex.

• (2) Assign weights $z_{i_p,p,1}, z_{i_p+1,p,1}, \dotsc , z_{j_p,p,1}$, to the $j_p - i_p + 1$ edges entering the central vertex, from bottom to top.

• (3) Assign weights $z_{i_p,p,2}, z_{i_p+1,p,2}, \dotsc , z_{j_p,p,2}$, to the $j_p - i_p + 1$ edges leaving the central vertex, from bottom to top.

For example, the star network $G = G_{J_1} \circ G_{J_2} = G_{[2,4]} \circ G_{[1,3]}$ is weighted as

(3.5)

and the weighted path matrix of G is

$$\begin{aligned} \begin{aligned} B&= \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} z_{2,1,1}z_{2,1,2} &{} z_{2,1,1}z_{3,1,2} &{} z_{2,1,1}z_{4,1,2} \\ 0 &{} z_{3,1,1}z_{2,1,2} &{} z_{3,1,1}z_{3,1,2} &{} z_{3,1,1}z_{4,1,2} \\ 0 &{} z_{2,1,1}z_{2,1,2} &{} z_{2,1,1}z_{3,1,2} &{} z_{2,1,1}z_{4,1,2} \end{bmatrix}\, \begin{bmatrix} z_{1,2,1}z_{1,2,2} &{} z_{1,2,1}z_{2,2,2} &{} z_{1,2,1}z_{3,2,2} &{} 0 \\ z_{2,2,1}z_{1,2,2} &{} z_{2,2,1}z_{2,2,2} &{} z_{2,2,1}z_{3,2,2} &{} 0 \\ z_{3,2,1}z_{1,2,2} &{} z_{3,2,1}z_{2,2,2} &{} z_{3,2,1}z_{3,2,2} &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{bmatrix}\\&= \begin{bmatrix} z_{1,1,1}z_{1,2,2} &{} z_{1,2,1}z_{2,2,2} &{} z_{1,2,1}z_{3,2,2} &{} 0 \\ z_{2,1,1}(z_D + z_U)z_{1,2,2} &{} z_{2,1,1}(z_D + z_U)z_{2,2,2} &{} z_{2,1,1}(z_D + z_U)z_{3,2,2} &{} z_{2,1,1}z_{4,1,2} \\ z_{3,1,1}(z_D + z_U)z_{1,2,2} &{} z_{3,1,1}(z_D + z_U)z_{2,2,2} &{} z_{3,1,1}(z_D + z_U)z_{3,2,2} &{} z_{3,1,1}z_{4,1,2} \\ z_{4,1,1}(z_D + z_U)z_{1,2,2} &{} z_{4,1,1}(z_D + z_U)z_{2,2,2} &{} z_{4,1,1}(z_D + z_U)z_{3,2,2} &{} z_{4,1,1}z_{4,1,2} \end{bmatrix}, \end{aligned}\nonumber \\ \end{aligned}$$

(3.6)

where we have defined $z_D = z_{2,1,2}z_{2,2,1}$, $z_U = z_{3,1,2}z_{3,2,1}$.

3.3 The Map $\sigma _B$ Associated with ${\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)$

The final, algebraic, object which we associate with the product ${\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)$ is a map $\sigma _B$ which allows us to evaluate a linear functional $\theta _q$ at this product by considering the corresponding generating function $\mathrm {Imm}_{\theta _q}(x) \in {\mathcal {A}}_{[n],[n]}$. This strategy can be quite helpful when one has a simpler expression for $\mathrm {Imm}_{\theta _q}(x)$ than for its coefficients $\theta _q(T_w)$. In our case, an expression for $\mathrm {Imm}_{\epsilon _q^\lambda }(x)$ is given by (2.12), while we have no explicit formula for $\epsilon _q^\lambda (T_w)$.

Let $Z_G$ be the quotient of the noncommutative ring

$$\begin{aligned} {\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}] \langle z_{h_p,p,k} \,|\, p=1,\dotsc , r; h_p = i_p, \dotsc , j_p; k = 1,2 \rangle \end{aligned}$$

modulo the ideal generated by the relations (3.4), and assume that $q^{\frac{1}{2}}$, $q^{\,\bar{\,}\frac{1}{2}}$ commute with all other indeterminates. Let $z_G$ be the product of all indeterminates $z_{h_p,p,k}$, in lexicographic order, and for $f \in Z_G$, let $[z_G]f$ denote the coefficient of $z_G$ in f. Let B be the weighted path matrix of G. We define $\sigma _B$ to be the ${\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$-linear map

$$\begin{aligned} \begin{aligned} \sigma _B: {\mathcal {A}}_{[n],[n]}&\rightarrow {\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]\\ x_{1,v_1} \,\cdots {x}_{n,v_n}&\mapsto [z_G] b_{1,v_1} \,\cdots {b}_{n,v_n}, \end{aligned} \end{aligned}$$

(3.7)

where $[z_G] b_{1,v_1} \,\cdots {b}_{n,v_n}$ denotes the coefficient of $z_G$ in $b_{1,v_1} \,\cdots {b}_{n,v_n}$, taken after $b_{1,v_1} \,\cdots {b}_{n,v_n}$ is expanded in the lexicographic basis of $Z_G$. Note that the “substitution” $x_{i,j} \mapsto b_{i,j}$ is performed only for monomials of the form $x^{e,v}$ in ${\mathcal {A}}_{[n],[n]}$: we define $\sigma _B(x^{u,w})$ by first expanding $x^{u,w}$ in the basis $\{ x^{e,v} \,|\, v \in {\mathfrak {S}}_n\}$, and then performing the substitution.

To illustrate the utility of the function $\sigma _B$, we consider both sides of the identity (1.6) when the product of Kazhdan–Lusztig basis elements is

$$\begin{aligned} {\widetilde{C}}_{s_{[2,4]}\,}(q) {\widetilde{C}}_{s_{[1,3]}\,}(q) = (1+q)\sum _{w \le 3421} T_w \in H_4(q), \end{aligned}$$

(3.8)

and when the linear function $\theta _q: H_4(q) \rightarrow {\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$ is defined by

$$\begin{aligned} \theta _q(T_w) = {\left\{ \begin{array}{ll} 1 &{}\quad \text {if }w = 3412,\\ -1 &{}\quad \text {if }w = 4312,\\ 0 &{}\quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

To compute the left-hand side of (1.6), we evaluate

$$\begin{aligned} \theta _q({\widetilde{C}}_{s_{[2,4]}\,}(q){\widetilde{C}}_{s_{[2,4]}\,}(q) ) = (1+q)(1) + (0)(-1) = 1+q \end{aligned}$$

(3.9)

since in (3.8) $T_{3412}$ has coefficient $1+q$ and $T_{4312}$ has coefficient 0. To compute the right-hand side of (1.6), we first write

$$\begin{aligned} \mathrm {Imm}_{\theta _q}(x) = q^{-2} x_{1,3}x_{2,4}x_{3,1}x_{4,2} - q^{\,\bar{\,}\frac{5}{2}} x_{1,4}x_{2,3}x_{3,1}x_{4,2} \end{aligned}$$

(3.10)

since $\ell (3412) = 4$ and $\ell (4312) = 5$. Now observe that the star network and weighted path matrix corresponding to ${\widetilde{C}}_{s_{[2,4]}\,}(q){\widetilde{C}}_{s_{[2,4]}\,}(q)$ are $G = G_{[2,4]} \circ G_{[1,3]}$ in (3.5) and B in (3.6). Thus, we compute $\sigma _B(\mathrm {Imm}_{\theta _q}(x))$ by substituting $x_{i,j} = b_{i,j}$ in (3.10) to obtain

$$\begin{aligned} \begin{aligned} q^{-2}b_{1,3}b_{2,4}b_{3,1}b_{4,2}&= q^{-2} z_{1,2,1}z_{3,2,2}z_{2,1,1}z_{4,1,2} z_{3,1,1}\\&\quad (z_D + z_U)z_{1,2,2}z_{4,1,1}(z_D + z_U)z_{2,2,2},\\ q^{\,\bar{\,}\frac{5}{2}} b_{1,4}b_{2,3}b_{3,1}b_{4,2}&= 0, \end{aligned} \end{aligned}$$

(3.11)

and extract the coefficient of $z_G = z_{1,2,1} z_{1,2,2} z_{2,1,1} \cdots z_{4,1,2}$ from these. Since $z_D^2$ and $z_U^2$ are not square-free, we ignore two monomials in the expansion of (3.11). Now, using the relations (3.4) to express the remaining two monomials in lexicographic order, we introduce multiples of $q^{\frac{1}{2}}$ for pairs $(z_{h_1,p,k}, z_{h_2,p,k})$ of variables sharing second and third indices,

Specifically, we introduce a multiple of $q^2$ for the monomial in which $z_D$ precedes $z_U$, and a multiple of $q^3$ in the other monomial. Thus, we have

$$\begin{aligned}{}[z_G] q^{-2} (q^2 + q^3) z_{1,2,1}z_{1,2,2}z_{2,1,1}z_D z_{2,2,2}z_{3,1,1}z_U z_{3,2,2}z_{4,1,1}z_{4,1,2} = 1+q, \end{aligned}$$

which matches (3.9), as desired.

The maps $\sigma$ behave well with respect to concatenation and matrix products. The following result was first proved in [11, Prop. 3.4] for the special case of wiring diagrams.

Proposition 3.1

Let star networks G, H have weighted path matrices B, C, respectively. Then for all $u,w \in {\mathfrak {S}}_n$ we have

$$\begin{aligned} \sigma _{BC}(x^{u,w}) = \sum _{v \in {\mathfrak {S}}_n} \sigma _B(x^{u,v}) \sigma _C(x^{v,w}). \end{aligned}$$

(3.12)

Proof

Write

$$\begin{aligned} G = G_{J_1} \circ \cdots \circ G_{J_k}, \qquad H = G_{J_{k+1}} \circ \cdots \circ G_{J_m}, \qquad J_p = [i_p, j_p], \end{aligned}$$

(3.13)

and let $A = (a_{i,j}) = BC$ be the weighted path matrix of $G \circ H$. Consider the expression

$$\begin{aligned} \begin{aligned} \sigma _{BC}(x^{u,w})&= [z_{G \circ H}]a_{u_1,w_1} \cdots a_{u_n,w_n}\\&= [z_{G \circ H}] \left( \sum _{t_1=1}^n b_{u_1,t_1} c_{t_1,w_1} \right) \cdots \left( \sum _{t_n=1}^n b_{u_n,t_n} c_{t_n,w_n} \right) . \end{aligned} \end{aligned}$$

Expanding the product of n sums we obtain $n^n$ terms, all but n! of which contribute 0 to the coefficient of $z_{G \circ H}$, because repeated indices among $t_1,\dotsc , t_n$ lead to repeated indeterminates or to matrix entries equal to 0. Thus we may consider only the n! terms in which $t_1, \dotsc , t_n$ are all distinct, and the expression reduces to

$$\begin{aligned}{}[z_{G \circ H}] \sum _{v \in {\mathfrak {S}}_n} b_{u_1,v_1}c_{v_1,w_1} \cdots b_{u_n,v_n}c_{v_n,w_n}. \end{aligned}$$

(3.14)

Now observe that $b_{u_i,v_i}$ commutes with $c_{v_j,w_j}$ for all i, j, since our indexing of intervals in (3.13) guarantees all edge weights $\{ z_{i_p, p, 1}, \dotsc , z_{j_p,p,1}, z_{i_p,p,2}, \dotsc , z_{j_p,p,2} \,|\, 1 \le p \le k\}$ of G to commute with all edge weights $\{ z_{i_p, p, 1}, \dotsc , z_{j_p,p,1}, z_{i_p,p,2}, \dotsc , z_{j_p,p,2} \,|\, k+1 \le p \le m\}$ of H. Thus, (3.14) is equal to

$$\begin{aligned} \begin{aligned} \sum _{v \in {\mathfrak {S}}_n} [z_{G \circ H}] b_{u_1,v_1} \cdots b_{u_n,v_n} c_{v_1,w_1} \cdots c_{v_n,w_n}&= \sum _{v \in {\mathfrak {S}}_n} [z_G] b_{u_1,v_1} \cdots b_{u_n,v_n} [z_H]\\ c_{v_1,w_1} \cdots c_{v_n,w_n} \\&= \sum _{v \in {\mathfrak {S}}_n} \sigma _B(x^{u,v}) \sigma _C(x^{v,w}). \end{aligned} \end{aligned}$$

$\square$

4 G-Tableaux and the Combinatorics of the Evaluation Map $\sigma _B$

Justification of the identity (1.6), which allows us to prove Theorem 6.5, depends upon a combinatorial interpretation of evaluations $\sigma _B(x^{u,v})$, which is stated in Proposition 4.5. This result and the preparatory Lemmas 4.1–4.4 extend earlier work in [5, §5–6] and [11, §3–4] on special cases of the evaluations.

First, we observe two cases in which such an evaluation is quite simple.

Lemma 4.1

Let star network $G = G_{J_1} \circ \cdots \circ G_{J_m}$ have weighted path matrix B, and fix $u, v \in {\mathfrak {S}}_n$.

• (1) If no path family of type $u^{-1}v$ covers G, then $\sigma _B(x^{u,v}) = 0$.

• (2) If exactly one path family of type v covers G, then $\sigma _B(x^{e,v}) = \smash {q^{\frac{\ell (v)}{2}}}$.

Proof

• (1) If no path family of type $u^{-1}v$ covers G, then we have $b_{u_1,v_1} \cdots b_{u_n,v_n} = 0$.

• (2) Suppose that there is exactly one path family $\pi$ of type v which covers G. Then for $i < j$, the pair $(v_i, v_j)$ is an inversion in v if and only if the paths $\pi _i$ and $\pi _j$ cross. Since $\pi$ is the unique path family of type v, the paths cannot cross more than once. If $\pi _i$, $\pi _j$ do not intersect, or intersect without crossing, then each variable in $\mathrm {wgt}(\pi _i)$ is lexicographically less than each variable in $\mathrm {wgt}(\pi _j)$. Relative to one another, all of these variables appear in lexicographic order in the expression

  $$\begin{aligned} \mathrm {wgt}(\pi ) = \mathrm {wgt}(\pi _1) \cdots \mathrm {wgt}(\pi _n) \end{aligned}$$

  (4.1)

  and contribute $q^0$ to the coefficient of $z_G$. On the other hand, if $\pi _i$, $\pi _j$ do intersect at the central vertex of $G_{J_p}$, then for some indices $a < b$, the variable $z_{b,p,2}$ appears in $\mathrm {wgt}(\pi _i)$, earlier in (4.1) than the lexicographically lesser variable $z_{a,p,2}$ which appears in $\mathrm {wgt}(\pi _j)$. By (3.4), this pair of variables contributes $q^{\frac{1}{2}}$ to the coefficient of $z_G$. $\square$

In other cases, the evaluation $\sigma _B(x^{u,v})$ is less simple, and we will interpret such an evaluation by covering a star network

$$\begin{aligned} G = G_{J_1} \circ \cdots \circ G_{J_m} \end{aligned}$$

(4.2)

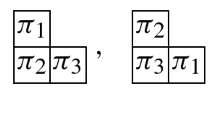
with a path family $\pi = (\pi _1, \dotsc , \pi _n)$ and arranging the component paths into a (French) Young diagram whose shape is some partition $\lambda$ of n. Following [5], we call the resulting structure a G-tableau, or more specifically a $\pi$-tableau of shape $\lambda$. If $\mathrm {type}(\pi ) = w$, we say that the tableau has type w. Since a $\pi$-tableau contains each path of $\pi$ exactly once, and since there are no constraints on where paths can be placed, there are always n! $\pi$-tableaux of a fixed shape $\lambda$. For example, consider $G = G_{[1,2]} \circ G_{[2,4]} \circ G_{[1,2]}$, pictured in (3.2). For any partition $\lambda \vdash 4$, there are $24^2$ G-tableaux of shape $\lambda$, since we have said that there are 24 path families covering G, and that there are 4! arrangements of any such family into four boxes. Five G-tableaux of shape 31 formed from the path families in (3.3),

can more specifically be called two $\pi$-tableaux (of type 1234), a $\rho$-tableau (of type 1234), a $\tau$-tableau (of type 1243), and an $\omega$-tableau (of type 3142).

Given a G-tableau U of shape $\lambda$, we define two Young tableaux L(U) and R(U) of shape $\lambda$ by replacing each path by its source and sink index, respectively. For example, by the definition of $\omega$ in (3.3), the $\omega$-tableau $U_5$ in (4.3) satisfies

We will sometimes omit boxes from a G-tableau or Young tableau when the tableau consists of a single row. In particular, a fixed path family $\pi$ of type v and a permutation $u \in {\mathfrak {S}}_n$ determine a single-row $\pi$-tableau

which we shall use often. This tableau satisfies

$$\begin{aligned} L(U(\pi , u, uv)) = u_1 \cdots u_n, \qquad R(U(\pi , u, uv)) = (uv)_1 \cdots (uv)_n. \end{aligned}$$

The inclusion of uv in our notation $U(\pi ,u,uv)$ is superfluous but makes clear the ordering of sinks as they appear in the tableau.

We define statistics on path families and on the tableaux containing them. Suppose that two paths $\pi _i$, $\pi _j$ pass through the central vertex of some simple star network $G_{J_p}$ in the factorization (4.2). We call the triple $(\pi _i, \pi _j, p) = (\pi _j, \pi _i, p)$ a crossing of $\pi$ if the two paths cross there, and a noncrossing otherwise. Define

$$\begin{aligned} \textsc {cr}(\pi ) = \# \{ (\pi _i, \pi _j, p) \,|\, (\pi _i, \pi _j, p) \text { is a crossing} \}. \end{aligned}$$

(4.5)

Suppose that the triple $(\pi _i, \pi _j, p)$ is a noncrossing, with $\pi _i$ entering and leaving the central vertex of $G_{J_p}$ below $\pi _j$. If U is any $\pi$-tableau, then we call the triple an inverted noncrossing of U if $\pi _j$ appears in an earlier column of U than does $\pi _i$. Define

$$\begin{aligned} \textsc {invnc}(U) = \# \{ (\pi _i, \pi _j, p) \,|\, (\pi _i, \pi _j, p) \text { is an inverted noncrossing in } U \}. \end{aligned}$$

(4.6)

For example, the four path families (3.3) satisfy

$$\begin{aligned} \begin{aligned} \textsc {cr}(\pi )&= 0,\\ \textsc {cr}(\rho )&= |\{(\rho _1, \rho _2, 1), (\rho _1, \rho _2, 3)\}| = 2,\\ \textsc {cr}(\tau )&= |\{ (\tau _1, \tau _2, 1), (\tau _3, \tau _4, 2), (\tau _1, \tau _2, 3)\}|= 3,\\ \textsc {cr}(\omega )&= |\{ (\omega _1, \omega _2, 1_), (\omega _1, \omega _4, 2), (\omega _3, \omega _4, 2)\}|= 3. \end{aligned} \end{aligned}$$

The five G-tableaux (4.3) satisfy

$$\begin{aligned} \begin{aligned} \textsc {invnc}(U_1)&= |\{(\pi _1, \pi _2, 1), (\pi _1, \pi _2, 3)\}|=2,\\ \textsc {invnc}(U_2)&= |\{(\pi _2, \pi _3, 2), (\pi _2, \pi _4, 2)\}|=2,\\ \textsc {invnc}(U_3)&= |\{(\rho _3, \rho _4, 2), (\rho _2, \rho _4, 2), (\rho _2, \rho _3, 2)\}|=3,\\ \textsc {invnc}(U_4)&= |\{(\tau _1, \tau _4, 2)\}|=1,\\ \textsc {invnc}(U_5)&= |\{(\omega _1, \omega _3, 2)\}|=1. \end{aligned} \end{aligned}$$

Now using the statistics $\textsc {cr}$ and $\textsc {invnc}$, we can combinatorially evaluate $\sigma _C(x^{u,v})$ in the case that G is a simple star network with weighted path matrix C.

Lemma 4.2

Fix an interval $J \subset [n]$ and let simple star network $G_J$ have weighted path matrix C. For $u,w \in {\mathfrak {S}}_n$ we have

$$\begin{aligned} \sigma _C(x^{u,w}) = {\left\{ \begin{array}{ll} q^{\frac{\textsc {cr}(\pi )}{2}} q^{\textsc {invnc}(U(\pi ,u,w))} &{}\quad \text {if }u^{-1}w \in {\mathfrak {S}}_{J},\\ 0 &{}\quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

(4.7)

where $\pi$ is the unique path family of type $u^{-1}w$ covering $G_J$.

Proof

We prove (4.7) by induction on $\ell (u)$. Observe first that for all $u \in {\mathfrak {S}}_n$, if $u^{-1}w \notin {\mathfrak {S}}_{J}$, then there is no path family of type $u^{-1}w$ which covers $G_J$. Thus the right-hand side of (4.7) is 0. By Lemma 4.1, the left-hand side is 0 as well. We may, therefore, concentrate on the first case, in which $u^{-1}w \in {\mathfrak {S}}_{J}$.

Suppose $\ell (u) = 0$. Then the left-hand side of (4.7) is $q^{\frac{\ell (w)}{2}}$ by Lemma 4.1. The right-hand side is also $q^{\frac{\textsc {cr}(\pi )}{2}} q^{\textsc {invnc}(U(\pi ,e,w))} = q^{\frac{\ell (w)}{2}} q^0$, since the left tableau $L(U(\pi ,e,w)) = 1 \cdots n$ guarantees that $U(\pi ,e,w)$ has no inverted noncrossings. Now suppose the claim to be true for $\ell (u) = 0,\dotsc , k$ and consider u of length $k+1$ with $u^{-1}w \in {\mathfrak {S}}_{J}$. Factor u as $u = s_iu'$ with $\ell (u') = k$. By (2.10), we have

$$\begin{aligned} \sigma _C(x^{u,w}) = \sigma _C(x^{s_iu'\,,\, w}) = {\left\{ \begin{array}{ll} \sigma _C(x^{u'\,,\,s_iw}) &{}\quad \text {if }s_iw > w,\\ \sigma _C(x^{u'\,,\,s_iw}) + (q^{\frac{1}{2}} - q^{\,\bar{\,}\frac{1}{2}})\sigma _C(x^{u'\,,\,w}) &{}\quad \text {if }s_iw < w. \end{array}\right. } \end{aligned}$$

By induction, and since $(u')^{-1}s_iw = u^{-1}w$, this is

$$\begin{aligned} {\left\{ \begin{array}{ll} q^{\frac{\textsc {cr}(\pi )}{2}} q^{\textsc {invnc}(U(\pi ,u'\,,\,s_iw))} &{}\text {if }s_iw > w,\\ q^{\frac{\textsc {cr}(\pi )}{2}} q^{\textsc {invnc}(U(\pi ,u'\,,\,s_iw))} + (q^{\frac{1}{2}} - q^{\,\bar{\,}\frac{1}{2}}) 0 &{}\text {if }s_iw< w\text { and }(u')^{-1}w \notin {\mathfrak {S}}_{J},\\ q^{\frac{\textsc {cr}(\pi )}{2}} q^{\textsc {invnc}(U(\pi ,u'\,,\,s_iw))} + (q^{\frac{1}{2}} - q^{\,\bar{\,}\frac{1}{2}})(q^{\frac{\textsc {cr}(\pi ')}{2}} q^{\textsc {invnc}(U(\pi ', u'\,,\,w))}) &{}\text {if }s_iw < w\text { and }(u')^{-1}w \in {\mathfrak {S}}_{J}, \end{array}\right. }\nonumber \\ \end{aligned}$$

(4.8)

where $\pi$, as in the statement of the lemma, is the unique path family of type $(u')^{-1}s_iw = u^{-1}w$ covering $G_J$, and where $\pi '$ is the unique path family of type $(u')^{-1}w = u^{-1}s_iw$ covering $G_J$ if $(u')^{-1}w \in {\mathfrak {S}}_{J}$.

Let us consider the two $G_J$-tableaux appearing in (4.8), and relate their crossings and inverted noncrossings to those of $U(\pi ,u,w)$.

The first tableau,

$$\begin{aligned} U(\pi , u'\,,\, s_iw) = \pi _{u_1} \cdots \pi _{u_{i-1}} \pi _{u_{i+1}} \pi _{u_i} \pi _{u_{i+2}} \cdots \pi _{u_n}, \end{aligned}$$

differs from $U(\pi , u, w)$ only by the transposition of paths $\pi _{u_i}$ and $\pi _{u_{i+1}}$. Thus, if $s_iw > w$, then we have $u_i > u_{i+1}$ and $w_i < w_{i+1}$, i.e., the paths $\pi _{u_i}$ and $\pi _{u_{i+1}}$ cross. It follows that we have $\textsc {invnc}(U(\pi ,u'\,,\,s_iw)) = \textsc {invnc}(U(\pi ,u,w))$, and the first case of (4.8) is $q^{\frac{\textsc {cr}(\pi )}{2}}q^{\textsc {invnc}(U(\pi ,u,w))}$.

On the other hand, if $s_iw < w$, then we have $u_i > u_{i+1}$ and $w_i > w_{i+1}$, i.e., the paths $\pi _{u_i}$ and $\pi _{u_{i+1}}$ do not cross. Suppose first that we have $(u')^{-1}w \notin {\mathfrak {S}}_{J}$. Then the paths $\pi _{u_i}$ and $\pi _{u_{i+1}}$ do not intersect, and the triple $(\pi _{u_i}, \pi _{u_{i+1}}, 1)$ is not an inverted noncrossing of $U(\pi ,u,w)$ or of $U(\pi ,u'\,,\, s_iw)$. Thus we have $\textsc {invnc}(U(\pi ,u'\,,\,s_iw)) = \textsc {invnc}(U(\pi ,u,w))$, and the second case of (4.8) is $q^{\frac{\textsc {cr}(\pi )}{2}}q^{\textsc {invnc}(U(\pi ,u,w))}$. Now suppose that we have $(u')^{-1}w \in {\mathfrak {S}}_{J}$. Then the paths $\pi _{u_i}$ and $\pi _{u_{i+1}}$ form a (noninverted) noncrossing in $U(\pi ,u'\,,\,s_iw)$ and an inverted noncrossing in $U(\pi ,u,w)$. It follows that we have

$$\begin{aligned} \textsc {invnc}(U(\pi ,u'\,,\,s_iw)) = \textsc {invnc}(U(\pi ,u,w)) - 1, \end{aligned}$$

(4.9)

and the first term of the third case of (4.8) is $q^{\frac{\textsc {cr}(\pi )}{2}}q^{\textsc {invnc}(U(\pi ,u,w))-1}$.

The second tableau,

$$\begin{aligned} \begin{aligned} U(\pi ', u'\,,\, w)&= \pi '_{u_1} \cdots \pi '_{u_{i-1}} \pi '_{u_{i+1}} \pi '_{u_i} \pi '_{u_{i+2}} \cdots \pi '_{u_n} \\&= \pi _{u_i} \cdots \pi _{u_{i-1}} \pi '_{u_{i+1}} \pi '_{u_i} \pi _{u_{i+2}} \cdots \pi _{u_n}, \end{aligned} \end{aligned}$$

differs from the tableau $U(\pi ,u,w)$ only in the pair $(\pi '_{u_{i+1}}, \pi '_{u_i})$ from sources $(u_{i+1}, u_i)$ to sinks $(w_i, w_{i+1})$, respectively. This pair forms a crossing $(\pi '_{u_{i+1}}, \pi '_{u_i}, 1)$ in $U(\pi '\,,\, u'\,,\,w)$ in place of the inverted noncrossing $(\pi _{u_i}, \pi _{u_{i+1}},1)$ in $U(\pi ,u,w)$. All other contributions to the differences $\textsc {cr}(\pi ) - \textsc {cr}(\pi ')$ and $\textsc {invnc}(U(\pi ,u,w)) - \textsc {invnc}(U(\pi ',u'\,,\, w))$ are due to paths $\pi _{u_j}$ from sources $u_j$ to sinks $w_j$ with indices j belonging to

$$\begin{aligned} Q_i :=\{ j \,|\, u_{i+1}< u_j< u_i; \ w_{i+1}< w_j < w_i \}. \end{aligned}$$

Each such path $\pi _{u_j}$ crosses neither $\pi _{u_i}$ nor $\pi _{u_{i+1}}$ in $\pi$, but crosses both $\pi '_{u_i}$ and $\pi '_{u_{i+1}}$ in $\pi '$. Similarly, for each such path $\pi _{u_j}$, exactly one of the triples $(\pi _{u_j}, \pi _{u_i},1)$, $(\pi _{u_j}, \pi _{u_{i+1}},1)$ is an inverted noncrossing in $\pi$ while neither of the triples $(\pi _{u_j}, \pi '_{u_i},1)$, $(\pi _{u_j}, \pi '_{u_{i+1}},1)$

is an inverted noncrossing in $\pi '$. Thus, we have

$$\begin{aligned} \begin{aligned}&\textsc {cr}(\pi ') = \textsc {cr}(\pi ) + 1 + 2|Q_i|,\\&\textsc {invnc}(U(\pi ',u'\,,\,w)) = \textsc {invnc}(U(\pi ,u,w)) - 1 - |Q_i|. \end{aligned} \end{aligned}$$

(4.10)

It follows that the second term in the third case of (4.8) is equal to

$$\begin{aligned} (q^{\frac{1}{2}} - q^{\,\bar{\,}\frac{1}{2}})q^{\frac{\textsc {cr}(\pi )+1 + 2|Q_i|}{2}} q^{\textsc {invnc}(U(\pi ,u,w)) - 1 - |Q_i|} = (q-1)q^{\frac{\textsc {cr}(\pi )}{2}} q^{\textsc {invnc}(U(\pi ,u,w))-1}, \end{aligned}$$

and the sum of the two terms in the third case of (4.8) is $q^{\frac{\textsc {cr}(\pi )}{2}}q^{\textsc {invnc}(U(\pi ,u,w))}$. In summary, all three cases of (4.8) are equal to this expression, as desired.

$\square$

Alternatively, when $G = G_J$ is a simple star network with weighted path matrix C, we can algebraically evaluate $\sigma _C(x^{u,w})$ in terms of the factorizations in (2.3).

Lemma 4.3

Let simple star network $G_J$ have weighted path matrix C, and let $u,w \in {\mathfrak {S}}_n$ have the unique ${\mathfrak {S}}_-^{J} \times {\mathfrak {S}}_{J}$ factorizations $u = u_- u^*$, $w = w_-w^*$. Then we have

$$\begin{aligned} \sigma _C(x^{u,w}) = {\left\{ \begin{array}{ll} \smash {q^{\frac{\ell (u^*)}{2}}}\smash {q^{\frac{\ell (w^*)}{2}}}&{}\quad \text {if }u^{-1}w \in {\mathfrak {S}}_{J},\\ 0 &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

Proof

By Lemma 4.2 it is sufficient to show that $\smash {q^{\frac{\ell (u^*)}{2}}}\smash {q^{\frac{\ell (w^*)}{2}}}= q^{\frac{\textsc {cr}(\pi )}{2}} q^{\textsc {invnc}(U(\pi ,u,w))}$, equivalently

$$\begin{aligned} \textsc {inv}(u^*) + \textsc {inv}(w^*) = \textsc {cr}(\pi ) + 2 \, \textsc {invnc}(U(\pi ,u,w)), \end{aligned}$$

(4.11)

whenever $u^{-1}w \in {\mathfrak {S}}_{J}$.

Consider a pair (i, j) with $i < j$ and the contributions of this pair and the triple $(\pi _i,\pi _j,1)$ to both sides of (4.11). If the paths do not intersect, then i or j does not belong to J and we have a contribution of 0 to both sides of (4.11). Assume, therefore, that the paths intersect.

If the triple $(\pi _i,\pi _j,1)$ is a crossing, then (i, j) is an inversion in exactly one of $u^*$ and $w^*$. Thus, we have a contribution of 1 to both sides of (4.11). On the other hand, if $(\pi _i,\pi _j,1)$ is a noncrossing, then $\pi _j$ intersects $\pi _i$ from above. Thus, $(\pi _i,\pi _j,1)$ is an inverted noncrossing if and only if $\pi _j$ precedes $\pi _i$ in $U(\pi ,u,w)$, i.e., if and only if j precedes i in u. But this condition is equivalent to j preceding i in w since $\pi _i$ and $\pi _j$ do not cross. Hence, we have a contribution of 2 to both sides of (4.11) or a contribution of 0 to both sides.

$\square$

To combinatorially evaluate expressions of the form $\sigma _B(x^{u,w})$, where B is the weighted path matrix of an arbitrary star network G, we will use the fact that G is a concatenation of smaller star networks. When a star network G decomposes as a concatenation $G' \circ H$, it is natural to similarly decompose any path family $\pi = (\pi _1, \dotsc , \pi _n)$ that covers G as $\pi = \pi ^{G'} \circ \pi ^H$, where $\pi ^{G'} = (\pi _1^{G'}, \dotsc , \pi _n^{G'})$, $\pi ^H = (\pi _1^H, \dotsc , \pi _n^H)$, and $\mathrm {type}(\pi ) = \mathrm {type}(\pi ^{G'}) \mathrm {type}(\pi ^H)$. One can also decompose a single path $\pi _i$ as $(\pi _i)^{G'} \circ (\pi _i)^H$ but one must be careful: if $\mathrm {type}(\pi ^{G'}) = y$ then we have $(\pi _i)^{G'} = (\pi ^{G'})_i = \pi _i^{G'}$, but $(\pi _i)^H = (\pi ^H)_{y_i}$, which is not in general equal to $(\pi ^H)_i = \pi _i^H$, the component path of $\pi ^H$ which starts at source i of H.

The above decompositions of path families and tableaux satisfy some simple identities.

Lemma 4.4

Let path family $\pi$ cover star network $G = G' \circ H$, and let $\pi ^{G'}$, $\pi ^H$ be its restrictions to $G'$, H. Then we have

$$\begin{aligned} \textsc {cr}(\pi ) = \textsc {cr}(\pi ^{G'}) + \textsc {cr}(\pi ^H). \end{aligned}$$

Now fix $u \in {\mathfrak {S}}_n$ and define $w = u \cdot \mathrm {type}(\pi )$, $v = u \cdot \mathrm {type}(\pi ^{G'})$. Then we have

$$\begin{aligned} \textsc {invnc}(U(\pi ,u,w)) = \textsc {invnc}(U(\pi ^{G'}\,,u,v)) + \textsc {invnc}(U(\pi ^H\,,v,w)). \end{aligned}$$

Proof

Write $G' = G_{J_1} \circ \cdots \circ G_{J_k}$, $H = G_{J_{k+1}} \circ \cdots \circ G_{J_m}$ and let paths $\pi _i$, $\pi _j$ intersect at the central vertex of some factor $G_{J_p}$. Suppose that this point of intersection is a crossing. Then it is a crossing of $\pi ^{G'}$ if $p \le k$ and a crossing of $\pi ^H$ if $p > k$. Thus, it contributes 1 to $\textsc {cr}(\pi )$ and 1 to either $\textsc {cr}(\pi ^{G'})$ (if $p \le k$) or $\textsc {cr}(\pi ^H)$ (if $p > k$).

Suppose on the other hand that the point of intersection is a noncrossing. Then it is a noncrossing of $\pi ^{G'}$ if $p \le k$ and a noncrossing of $\pi ^H$ if $p > k$. Moreover, $\pi _i$ enters and departs from the central vertex of $G_{J_p}$ above $\pi _j$ if and only if the restrictions of these paths to $G'$ or H do the same.

Now consider the positions of these paths in their respective tableaux. Let a, b, be the positions of $\pi _i$ and $\pi _j$ in $U(\pi ,u,w)$: $\pi _i = \pi _{u_a}$, $\pi _j=\pi _{u_b}$, and assume without loss of generality that $a < b$. Then the restrictions of the two paths to $G'$ and H also appear in positions a and b, for we have

Tableau	Path in position a	Path in position b
$U(\pi ,u,w)$	$\pi _{u_a}$ From source $u_a$ of G to sink $w_a$	$\pi _{u_b}$ From source $u_b$ of G to sink $w_b$
$U(\pi ^{G'},u,v)$	$\pi _{u_a}^{G'}$ From source $u_a$ of $G'$ to sink $v_a$	$\pi _{u_b}^{G'}$ From source $u_b$ of $G'$ to sink $v_b$
$U(\pi ^H,v,w)$	$\pi _{v_a}^H$ From source $v_a$ of H to sink $w_a$	$\pi _{u_b}^H$ From source $v_b$ of H to sink $w_b$

with $\pi _{u_a} = \pi _{u_a}^{G'} \circ \pi _{v_a}^H$, $\pi _{u_b} = \pi _{u_b}^{G'} \circ \pi _{v_b}^H$. Thus, the triple $(\pi _{u_a}, \pi _{u_b}, p)$ contributes 1 to $\textsc {invnc}(U(\pi ,u,w))$ if and only if $(\pi _{u_a}^{G'}, \pi _{u_b}^{G'}, p)$ contributes 1 to $\textsc {invnc}(U(\pi ^{G'},u,v))$ ($p \le k$), or $(\pi _{u_a}^H, \pi _{u_b}^H, p)$ contributes 1 to $\textsc {invnc}(U(\pi ^H,v,w))$ ($p > k$). $\square$

Combining the simple star network evaluation $\sigma _C(x^{u,w})$ from Lemma 4.2 with the identities in Lemma 4.4, we can now inductively prove a combinatorial evaluation of $\sigma _B(x^{u,w})$ where B is the weighted path matrix of an arbitrary star network.

Proposition 4.5

Let star network G have weighted path matrix B. For $u,w \in {\mathfrak {S}}_n$ we have

$$\begin{aligned} \sigma _B (x^{u,w}) = \sum _\pi q^{\frac{\textsc {cr}(\pi )}{2}} q^{\textsc {invnc}(U(\pi ,u,w))}, \end{aligned}$$

(4.12)

where the sum is over path families $\pi$ of type $u^{-1}w$ covering G.

Proof

By Lemma 4.2, the claim is true when G is the simple star network $G_{[i_1,j_1]}$.

Now suppose the claim is true for G a concatenation of $1, \dotsc , m$ simple star networks and consider $G = G' \circ H$, where $G' = G_{J_1} \circ \cdots \circ G_{J_m}$ and $H = G_{J_{m+1}}$. Let $B'$, C be the path matrices of $G'$, H, respectively, so that $B = B'C$ is the path matrix of G.

By Proposition 3.1 and induction, we have

$$\begin{aligned} \sigma _{B'C}(x^{u,w}) = \sum _{t \in {\mathfrak {S}}_{J_{m+1}}} \sum _{\pi ^{G'}} q^{\frac{\textsc {cr}(\pi ^{G'})}{2}} q^{\textsc {invnc}(U(\pi ^{G'}\,,u,wt^{-1}))}\nonumber \\ q^{\frac{\textsc {cr}(\pi ^H)}{2}} q^{\textsc {invnc}(U(\pi ^H,wt^{-1},w))}, \end{aligned}$$

(4.13)

where $\pi ^{G'}$ varies over all path families of type $u^{-1}wt^{-1}$ which cover $G'$. Since pairs of path families of types $u^{-1}wt^{-1}$ and t covering $G'$ and H, respectively, correspond to path families of type $u^{-1}w$ covering G, we may apply Lemma 4.4 to the right-hand side above to obtain

$$\begin{aligned} \sum _\pi q^{\frac{\textsc {cr}(\pi )}{2}} q^{\textsc {invnc}(U(\pi ,u,w))}, \end{aligned}$$

where the sum is over all path families $\pi$ of type $u^{-1}w$ which cover G. $\square$

5 Products ${\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)$ and the q-Immanant Evaluation Theorem

We complete our justification of the crucial identity (1.6) in Theorem 5.2, first using Proposition 5.1 to relate evaluations of the form $\sigma _B(x^{e,w})$ to coefficients in the natural expansion of ${\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)$. As a corollary, we obtain a second interpretation of these coefficients which generalizes a result of Deodhar [7, Prop. 3.5].

The following two results generalize [11, Prop. 3.6 – Thm. 3.7].

Proposition 5.1

Let star network $G = G_{J_1} \circ \cdots \circ G_{J_m}$ have weighted path matrix B, and fix $w \in {\mathfrak {S}}_n$. Then the coefficient of $T_w$ in ${\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)$ is equal to $q^{\,\bar{\,}\frac{\ell (w)}{2}}\sigma _B(x^{e,w})$.

Proof

Consider the simple star network $G = G_{J_1}$ and its weighted path matrix B. By Lemma 4.3, we have

$$\begin{aligned} \sigma _B(x^{e,w}) = {\left\{ \begin{array}{ll} \smash {q^{\frac{\ell (w)}{2}}}&{}\quad \text {if }w \in {\mathfrak {S}}_{J_1},\\ 0 &{}\quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

Since ${\widetilde{C}}_{s_{J_1}\,}(q) = \sum _{w \in {\mathfrak {S}}_{J_1}} T_w$, the result is true for any simple star network.

Now assume that the result holds for concatenations of $1,\dotsc , m-1$ simple star networks, and define $\{ a_w \,|\, w \in {\mathfrak {S}}_n\} \subseteq {\mathbb {Z}}[q]$ by

$$\begin{aligned} {\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_{m-1}}\,}(q) = \sum _{w \in {\mathfrak {S}}_n} a_w T_w. \end{aligned}$$

Consider the star network $G = G_{J_1} \circ \cdots \circ G_{J_m}$ with weighted path matrix B and decompose G as $G' \circ H$, where $G' = G_{J_1} \circ \cdots \circ G_{J_{m-1}}$ has weighted path matrix $B'$ and $H = G_{J_m}$ has weighted path matrix C. By Proposition 3.1, we have

$$\begin{aligned} \sigma _B(x^{e,w}) = \sum _{u \in {\mathfrak {S}}_{J_m}} \sigma _{B'}(x^{e,wu^{-1}}) \sigma _C(x^{wu^{-1},w}), \end{aligned}$$

where we sum over $u \in {\mathfrak {S}}_{J_m}$ because $\sigma _C(x^{wu^{-1},w})=0$ otherwise. Now factor w as $w_- w^*$ with $w_- \in {\mathfrak {S}}_-^{J_m}$, $w^* \in {\mathfrak {S}}_{J_m}$, and define $t = w^* u^{-1}$ so that we have $wu^{-1} = w_-w^* (w^*)^{-1}t = w_-t$. Making this substitution in the sum and observing that as u varies over ${\mathfrak {S}}_{J_m}$, so does t, we apply Lemma 4.3 to the second factor in each summand to obtain

$$\begin{aligned}&\sum _{t \in {\mathfrak {S}}_{J_m}} \,\sigma _{B'} (x^{e,w_-t}) \sigma _C (x^{w_-t,w}) = \sum _{t \in {\mathfrak {S}}_{J_m}} \,\sigma _{B'} (x^{e,w_-t}) \smash {q^{\frac{\ell ((w_-t)^*)}{2}}}\smash {q^{\frac{\ell (w^*)}{2}}}\\&\quad = \, \smash {q^{\frac{\ell (w^*)}{2}}}\,\sum _{t \in {\mathfrak {S}}_{J_m}} \,\sigma _{B'}(x^{e,w_-t}) \smash {q^{\frac{\ell (t)}{2}}}. \end{aligned}$$

By induction, this is

$$\begin{aligned}&\smash {q^{\frac{\ell (w^*)}{2}}}\,\sum _{t \in {\mathfrak {S}}_{J_m}} \,\smash {q^{\frac{\ell (w_-t)}{2}}}a_{w_-t} \smash {q^{\frac{\ell (t)}{2}}}= \, \smash {q^{\frac{\ell (w^*)}{2}}}\,\sum _{t \in {\mathfrak {S}}_{J_m}} \,\smash {q^{\frac{\ell (w_-)}{2}}}\smash {q^{\frac{\ell (t)}{2}}}a_{w_-t} \smash {q^{\frac{\ell (t)}{2}}}\\&\quad = \, \smash {q^{\frac{\ell (w)}{2}}}\,\sum _{t \in {\mathfrak {S}}_{J_m}}\,a_{w_-t} q^{\ell (t)}, \end{aligned}$$

and we have

$$\begin{aligned} q^{\,\bar{\,}\frac{\ell (w)}{2}}\sigma _B(x^{e,w}) = \sum _{t \in {\mathfrak {S}}_{J_m}}\,a_{w_-t} q^{\ell (t)}. \end{aligned}$$

(5.1)

On the other hand, consider the element

$$\begin{aligned} {\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q) = \left( \sum _{w \in {\mathfrak {S}}_n} a_w T_w \right) {\widetilde{C}}_{s_{J_m}\,}(q) = \sum _{w \in {\mathfrak {S}}_n} a_w T_{w_-} T_{w^*} {\widetilde{C}}_{s_{J_m}\,}(q).\nonumber \\ \end{aligned}$$

(5.2)

By (2.4), this is

$$\begin{aligned}&\sum _{y \in {\mathfrak {S}}_-^{J_m}} \,T_y \,\sum _{t \in {\mathfrak {S}}_{J_m}} \,a_{yt} T_t {\widetilde{C}}_{s_{J_m}\,}(q) = \sum _{y \in {\mathfrak {S}}_-^{J_m}} \,T_y {\widetilde{C}}_{s_{J_m}\,}(q) \,\sum _{t \in {\mathfrak {S}}_{J_m}} \,a_{yt} q^{\ell (t)} \\&\quad = \sum _{y \in {\mathfrak {S}}_-^{J_m}} \,T_y \,\sum _{v \in {\mathfrak {S}}_{J_m}} \,T_v \,\sum _{t \in {\mathfrak {S}}_{J_m}} \,a_{yt} q^{\ell (t)}, \end{aligned}$$

and in the last expression, we obtain $T_w = T_yT_v$ precisely when $y = w_-$, $v = w^*$. Thus, the coefficient of $T_w$ in this expression is (5.1). $\square$

Now we have a quick proof of the q-immanant evaluation theorem for star networks.

Theorem 5.2

Let $\theta _q: H_n(q)\rightarrow {\mathbb {Z}}[q^{\frac{1}{2}}, q^{\,\bar{\,}\frac{1}{2}}]$ be linear, and let star network $G = G_{J_1} \circ \cdots \circ G_{J_m}$ have weighted path matrix B. Then we have

$$\begin{aligned} \theta _q({\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)) = \sigma _B(\mathrm {Imm}_{\theta _q}(x)). \end{aligned}$$

(5.3)

Proof

Write ${\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q) = \sum _{w \in {\mathfrak {S}}_n} a_w T_w$. Then the right-hand side of (5.3) is

$$\begin{aligned}&\sigma _B \left( \sum _{w \in {\mathfrak {S}}_n} \theta _q(T_w) q^{\,\bar{\,}\frac{\ell (w)}{2}}x^{e,w} \right) = \sum _{w \in {\mathfrak {S}}_n} \theta _q(T_w) q^{\,\bar{\,}\frac{\ell (w)}{2}}\sigma _B(x^{e,w}) \\&\quad = \sum _{w\in {\mathfrak {S}}_n} \theta _q(T_w) a_w = \theta _q \left( \sum _{w \in {\mathfrak {S}}_n} a_wT_w \right) , \end{aligned}$$

where the second equality follows from Proposition 5.1. But this is the left-hand side of (5.3). $\square$

Proposition 5.1 and the special case $u = e$ of Proposition 4.5 yield a proof of a generalization of Deodhar’s defect formula [7, Prop. 3.5] for coefficients in the expansion of $(1 + T_{s_{i_1}}) \cdots (1 + T_{s_{i_m}})$, which we will use in Sect. 6. Let $\pi = (\pi _1, \dotsc , \pi _n)$ be a path family covering a star network $G = G_{J_1} \circ \cdots \circ G_{J_m}$. If two paths $\pi _i$, $\pi _j$ intersect at the central vertex of $G_{J_p}$, call the triple $(\pi _i, \pi _j, p)$ defective or a defect if the paths have previously crossed an odd number of times (i.e., in $G_{J_1}, \dotsc , G_{J_{i_{p-1}}}$). Let $\textsc {d}(\pi )$ denote the number of defects of $\pi$,

$$\begin{aligned} \textsc {d}(\pi ) = \# \{(\pi _i, \pi _j, p) \,|\, (\pi _i, \pi _j, p) \text { defective} \}. \end{aligned}$$

(5.4)

The original definition of $\textsc {d}(\pi )$ given in [7, Defn. 2.2] (as interpreted in [2, Rmk. 6]) and used throughout [11] is simply the number of indices p appearing in defective triples $(\pi _i, \pi _j, p)$, since each simple star network $G_{J_p} = G_{[j_p,j_p+1]}$ considered in those papers completely determines the two paths to intersect at its central vertex.

Corollary 5.3

The coefficients in the expansion ${\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q) = \underset{w}{\sum }a_w T_w$ are given by

$$\begin{aligned} a_w = \sum _\pi q^{\textsc {d}(\pi )}, \end{aligned}$$

where the sum is over all path families of type w which cover the star network $G_{J_1} \circ \cdots \circ G_{J_m}$.

Proof

Substitute $u = e$ in Proposition 4.5. The right-hand side of (4.12) is a sum over path families $\pi$ of type w, and each tableau $U = U(\pi ,e,w)$ is simply the sequence $\pi = (\pi _1,\dotsc ,\pi _n)$. Thus, an inverted noncrossing of U is simply a noncrossing in which the upper path has index less than that of the lower path, i.e., a defective noncrossing. To relate these to all defects, let us temporarily define

$$\begin{aligned} \begin{aligned} \textsc {dnc}(\pi )&= \text {number of defective noncrossings of }\pi ,\\ \textsc {dc}(\pi )&= \text {number of defective crossings of }\pi , \end{aligned} \end{aligned}$$

so that $\textsc {d}(\pi ) = \textsc {dnc}(\pi ) + \textsc {dc}(\pi )$. Now observe that for any path family of type w we have

$$\begin{aligned} \textsc {cr}(\pi ) = \textsc {inv}(w) + 2\textsc {dc}(\pi ) \end{aligned}$$

because if paths $\pi _a$, $\pi _b$ cross k times, then at most one of those crossings contributes to $\textsc {inv}(w)$, while exactly half of the remaining crossings are defective. Thus, the right-hand side of (4.12) becomes

$$\begin{aligned} \sum _\pi q^{\frac{\textsc {inv}(w) + 2\textsc {dc}(\pi )}{2}} q^{\textsc {dnc}(\pi )} = \sum _\pi \smash {q^{\frac{\ell (w)}{2}}}q^{\textsc {dc}(\pi )+\textsc {dnc}(\pi )} = \smash {q^{\frac{\ell (w)}{2}}}\sum _\pi q^{\textsc {d}(\pi )}, \end{aligned}$$

(5.5)

where the sum is over all path families of type w which cover the star network $G_{J_1} \circ \cdots \circ G_{J_m}$.

By Proposition 5.1, the left-hand side of (4.12) is $\smash {q^{\frac{\ell (w)}{2}}}a_w$. Combining this with (5.5), we have the desired result. $\square$

6 Evaluation of Induced Sign Characters

We now complete the solution of Problem 1.1 by providing a combinatorial interpretation in Theorem 6.5 for all expressions of the form

$$\begin{aligned} \epsilon _q^\lambda ({\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)), \end{aligned}$$

(6.1)

with $\lambda \vdash n$ and $(J_1,\dotsc ,J_m)$ a sequence of subintervals of [n]. Strengthening [11, Thm. 5.4], Theorem 6.5 relies upon definitions and results which are more general than those given in [11, §5]. For the convenience of the reader, we will state and prove all necessary lemmas from scratch, even when the changes from corresponding results of [11, §5] are minor.

By Theorem 5.2 and Equation (2.14), each expression (6.1) is equal to

$$\begin{aligned} \sigma _B(\mathrm {Imm}_{\epsilon _q^\lambda }(x)) = \sum _{u \in \smash {{\mathfrak {S}}_\lambda ^{-}}} \sum _{y \in {\mathfrak {S}}_\lambda } (-1)^{\ell (y)} q^{\,\bar{\,}\frac{\ell (y)}{2}} \sigma _B(x^{u,yu}), \end{aligned}$$

(6.2)

where B is the weighted path matrix of the star network $G = G_{J_1} \circ \cdots \circ G_{J_m}$. Thus, it suffices to combinatorially interpret the right-hand side of (6.2). To do this, we will apply Proposition 4.5 to each expression $\sigma _B(x^{u,yu})$ and will compute statistics for tableaux belonging to the set

$$\begin{aligned} {\mathcal {U}}_I = {\mathcal {U}}_I(G) :=\{ U(\pi , u, yu ) \,|\, \pi \text { covers } G, u = u(I), y \in {\mathfrak {S}}_\lambda \}, \end{aligned}$$

where $I \mapsto u(I)$ is the bijection defined after (2.13). Note that for each k, our restriction on y forces the sink indices of paths in components

$$\begin{aligned} (\lambda _1 + \cdots + \lambda _{k-1}+1), \dotsc , (\lambda _1 + \cdots + \lambda _k) \end{aligned}$$

(6.3)

of $U(\pi ,u,yu)$ to be a permutation of the source indices of the same paths.

We will apply a sign-reversing involution to the tableaux in each set ${\mathcal {U}}_I$ by defining an involution on a second set ${\mathcal {T}}_I$ of tableaux, in obvious bijection with ${\mathcal {U}}_I$. For a star network G let ${\mathcal {T}}_I = {\mathcal {T}}_I(G)$ be the set of all column-closed, left column-strict G-tableaux W of shape $\lambda ^{\, \top \,}$ such that $L(W^{\, \top \,})_k = I_k$ (as sets) for $k = 1,\dotsc ,r$. Define the bijection

$$\begin{aligned} \begin{aligned} \delta = \delta _I\,: {\mathcal {U}}_I&\rightarrow {\mathcal {T}}_I\\ U&\mapsto W \end{aligned} \end{aligned}$$

(6.4)

by letting W be the left column-strict G-tableau of shape $\lambda ^{\, \top \,}$ whose kth column consists of paths in components (6.3) of U.

Since $U \in {\mathcal {U}}_I$ and $\delta (U) \in {\mathcal {T}}_I$ contain the same path family, it is easy to see that $\delta$ does not affect the statistic $\textsc {cr}$. On the other hand, it changes the statistic $\textsc {invnc}$ in a very simple way. For any G-tableau V, define $\textsc {cdnc}(V)$ to be the number of defective noncrossings of pairs of paths appearing in the same column of V.

Lemma 6.1

Let I be an ordered set partition. For $U \in {\mathcal {U}}_I$ we have

$$\begin{aligned} \textsc {invnc}(U) = \textsc {invnc}(\delta (U)) + \textsc {cdnc}(\delta (U)). \end{aligned}$$

(6.5)

Proof

Let $\lambda = (\lambda _1, \dotsc , \lambda _r)$ be the type of I, and let $\pi$ be the path family in a G-tableau U, where $G = G_{J_1} \circ \cdots \circ G_{J_m}$. Choose an index p, $1 \le p \le m$ and let $\pi _a$, $\pi _b$ be two paths which intersect at the central vertex of $G_{J_p}$, with $\pi _b$ entering above $\pi _a$. For some k, $\pi _b$ appears among the entries

$$\begin{aligned} (\lambda _1 + \cdots + \lambda _{k-1} + 1), \dotsc , (\lambda _1 + \cdots + \lambda _k) \end{aligned}$$

(6.6)

of U. The indices of these $\lambda _k$ paths increase from left to right in U, since the indices of all paths in U form the permutation $u = u(I) \in {\mathfrak {S}}_\lambda ^{-}$ (2.6). Suppose that the triple $(\pi _a, \pi _b, p)$ contributes 1 to $\textsc {invnc}(U)$. Then $\pi _b$ appears earlier than $\pi _a$ in U. If $\pi _a$ appears among the entries (6.6), then we must have $b < a$. Thus, $\pi _a, \pi _b$ both appear in column k of $\delta (U)$, and the triple contributes 0 to $\textsc {invnc}(\delta (U))$ and 1 to $\textsc {cdnc}(\delta (U))$. On the other hand, if $\pi _a$ does not appear in entries (6.6) of U, then it appears strictly to the right of column k of $\delta (U)$. Thus, the triple contributes 1 to $\textsc {invnc}(\delta (U))$ and 0 to $\textsc {cdnc}(\delta (U))$. In all cases, the contribution to the right-hand-side of (6.5) is 1.

Now suppose that the triple ($\pi _a, \pi _b, p$) contributes 0 to $\textsc {invnc}(U)$. If $\pi _a$ and $\pi _b$ cross in $G_{J_p}$, then the triple contributes 0 to $\textsc {invnc}(\delta (U))$ and $\textsc {cdnc}(\delta (U))$. If $\pi _a$ and $\pi _b$ do not cross in $G_{J_p}$, then $\pi _a$ appears before $\pi _b$ in U. If $\pi _a$ appears before the entries (6.6) of U, then in $\delta (U)$ it appears in an earlier column than $\pi _b$ and the triple contributes 0 to $\textsc {invnc}(\delta (U))$ and $\textsc {cdnc}(\delta (U))$. If $\pi _a$ appears as one of the entries (6.6) of U, then it appears in the same column of $\delta (U)$ as $\pi _b$ and satisfies $a < b$. Again the triple contributes 0 to $\textsc {invnc}(\delta (U))$ and $\textsc {cdnc}(\delta (U))$. In both cases the contribution to the right-hand-side of (6.5) is 0. $\square$

Now we define the involution

$$\begin{aligned} \zeta = \zeta _I\,: {\mathcal {T}}_I \rightarrow {\mathcal {T}}_I \end{aligned}$$

(6.7)

(different from $\zeta$ in [11]) as follows. Let $G = G_{J_1} \circ \cdots \circ G_{J_m}$, $u = u(I)$, and $\lambda = \mathrm {type}(I)$. Fix $y \in {\mathfrak {S}}_\lambda$ and let $W = \delta (U(\pi ,u,yu))$.

• (1) If W is column-strict, then define $\zeta (W) = W$.

• (2) Otherwise,

  • (a) Let t be the greatest index such that column t of W is not column-strict.

  • (b) Let p be the greatest index such that (at least) two paths in column t of W pass through the interior vertex of $G_{J_p}$.

  • (c) Let j, $j'$ be the two positions in the interval $[\lambda _1 + \cdots + \lambda _{t-1} + 1, \lambda _1 + \cdots \lambda _t]$ for which paths $\pi _{u_j}$, $\pi _{u_{j'}}$ have the right-to-left lexicographically greatest pair $((yu)_j,(yu)_{j'})$ of sink indices.

  • (d) Let ${\hat{\pi }} = ({\hat{\pi }}_1, \dotsc , {\hat{\pi }}_n)$ be the path family obtained from $\pi$ by swapping the terminal subpaths of $\pi _{u_j}$ and $\pi _{u_{j'}}$, beginning at the interior vertex of $G_{J_p}$. (${\hat{\pi }}_i = \pi _i$ for $i \notin \{u_j,u_{j'}\}.$)

  • (e) Define $\zeta (W)$ to be the tableau obtained from W by replacing $\pi _i$ by ${\hat{\pi }}_i$, for $i = 1,\dotsc ,n$.

If $W \in {\mathcal {T}}_I$ is not a fixed point of $\zeta$, then the tableaux $U, {\widehat{U}} \in {\mathcal {U}}_I$ satisfying $\delta (U) = W$, $\delta ({\widehat{U}}) = \zeta (W)$ are closely related.

Lemma 6.2

Let $I = (I_1, \dotsc I_r)$ be an ordered set partition of type $\lambda$, and define $u = u(I)$.

Let G-tableaux $W \in {\mathcal {T}}_I$ and $U, {\widehat{U}} \in {\mathcal {U}}_I$ satisfy $W = \delta (U) \ne \zeta (W) = \delta ({\widehat{U}})$, and define path families $\pi$, ${\hat{\pi }}$ as above. Then for some generator $s \in {\mathfrak {S}}_\lambda$ and some permutations $y, {\hat{y}} = ys \in {\mathfrak {S}}_\lambda$ we have $U = U(\pi , u, yu)$, ${\widehat{U}} = U({\hat{\pi }}, u, {\hat{y}} u)$.

Proof

The tableaux U, ${\widehat{U}}$ contain the same path families as W and $\zeta (W)$, respectively, and these path families are $\pi$, ${\hat{\pi }}$, as defined in the definition of $\zeta$.

Listing the source indices of paths in column t of W, from bottom to top, we obtain the increasing sequence

$$\begin{aligned} (u_{\lambda _1 + \cdots + \lambda _{t-1}+1}, u_{\lambda _1 + \cdots + \lambda _{t-1}+2}, \dotsc , u_{\lambda _1 + \cdots + \lambda _{t}}). \end{aligned}$$

(6.8)

Since elements of ${\mathcal {T}}_I$ are column-closed, the sink indices of the paths form a permutation of this sequence,

$$\begin{aligned} ((yu)_{\lambda _1 + \cdots + \lambda _{t-1}+1}, (yu)_{\lambda _1 + \cdots + \lambda _{t-1}+2}, \dotsc , (yu)_{\lambda _1 + \cdots + \lambda _{t}}), \end{aligned}$$

for some $y \in {\mathfrak {S}}_\lambda$. In particular, the sink indices $(yu)_j$ and $(yu)_{j'}$ of $\pi _{u_j}$, $\pi _{u_{j'}}$ are simply two components $u_i$ and $u_{i'}$ of (6.8).

By our choice of p, no two paths in column t of W intersect to the right of $G_{J_p}$. By our choice of j and $j'$, no path in this column has a sink index strictly between $u_i$ and $u_{i'}$. It follows that $|i - i'| = 1$. Thus, the sink indices of the path family ${\hat{\pi }}$ are given by ${\hat{y}}u = ysu$, where s is the adjacent transposition $s_{\min \{i,i'\}} \in {\mathfrak {S}}_\lambda$. $\square$

Furthermore, when $W \in {\mathcal {T}}_I$ is not a fixed point of $\zeta$, the values of the statistics $\textsc {cr}$, $\textsc {invnc}$ and $\textsc {cdnc}$ on W and $\zeta (W)$ are closely related, as are $\ell (y)$ and $\ell ({\hat{y}})$, where y, ${\hat{y}}$ are defined as in Lemma 6.2.

Lemma 6.3

Let $W = U(\pi ,u,yu) \ne \zeta (W) = U({\hat{\pi }}, u, {\hat{y}}u)$ be as above with ${\hat{\pi }}$ being defined by the intersection of $\pi _{u_j}$ and $\pi _{u_{j'}}$ in $G_{J_p}$. Let b be the number of paths in $\pi$ (equivalently, in ${\hat{\pi }}$) which enter $G_{J_p}$ between the paths $\pi _{u_j}$ and $\pi _{u_{j'}}$, and which leave $G_{J_p}$ between the same two paths. Then we have

$$\begin{aligned} \ell ({\hat{y}})= & {} {\left\{ \begin{array}{ll} \ell (y) - 1 &{}\text {if }(\pi _{u_j}, \pi _{u_{j'}}, p)\text { is a proper crossing or defective noncrossing}, \\ \ell (y) + 1 &{}\text {if }(\pi _{u_j}, \pi _{u_{j'}}, p)\text { is a proper noncrossing or defective crossing}; \end{array}\right. } \end{aligned}$$

(6.9)

$$\begin{aligned} \textsc {cr}({\hat{\pi }})= & {} {\left\{ \begin{array}{ll} \textsc {cr}(\pi ) - 1 - 2b &{}\text {if }(\pi _{u_j}, \pi _{u_{j'}}, p) \text { is a crossing},\\ \textsc {cr}(\pi ) + 1 + 2b &{}\text {otherwise}; \end{array}\right. } \end{aligned}$$

(6.10)

$$\begin{aligned} \textsc {invnc}(\zeta (W))= & {} {\left\{ \begin{array}{ll} \textsc {invnc}(W) + b &{}\text {if }(\pi _{u_j}, \pi _{u_{j'}}, p)\text { is a crossing},\\ \textsc {invnc}(W) - b &{}\text {otherwise}; \end{array}\right. } \end{aligned}$$

(6.11)

$$\begin{aligned} \textsc {cdnc}({\hat{\pi }})= & {} {\left\{ \begin{array}{ll} \textsc {cdnc}(\pi ) &{}\text {if }(\pi _{u_j}, \pi _{u_{j'}}, p)\text { is proper},\\ \textsc {cdnc}(\pi ) - 1 &{}\text {if }(\pi _{u_j}, \pi _{u_{j'}}, p)\text { is a defective noncrossing},\\ \textsc {cdnc}(\pi ) + 1 &{}\text {if }(\pi _{u_j}, \pi _{u_{j'}}, p)\text { is a defective crossing}. \end{array}\right. } \end{aligned}$$

(6.12)

Proof

(Identity (6.9)). Recall that we have

$$\begin{aligned} \begin{aligned} \text {source}(\pi _{u_j}) = \text {source}({\hat{\pi }}_{u_j}) = u_j,\\ \text {source}(\pi _{u_{j'}}) = \text {source}({\hat{\pi }}_{u_{j'}}) = u_{j'}, \end{aligned} \qquad \begin{aligned}&\text {sink}(\pi _{u_j}) = \text {sink}({\hat{\pi }}_{u_{j'}}) = (yu)_j,\\&\text {sink}(\pi _{u_{j'}}) = \text {sink}({\hat{\pi }}_{u_j}) = (yu)_{j'} > (yu)_j. \end{aligned} \end{aligned}$$

By Lemma 6.2, we have $y, {\hat{y}} = ys \in {\mathfrak {S}}_\lambda$ and therefore $\ell ({\hat{y}}) = \ell (y) \pm 1$. Since $u \in {\mathfrak {S}}_\lambda ^{-}$, we also have

$$\begin{aligned} \ell (yu) = \ell (y) + \ell (u), \qquad \ell ({\hat{y}}u) = \ell ({\hat{y}}) + \ell (u). \end{aligned}$$

(6.13)

If $(\pi _{u_j}, \pi _{u_{j'}}, p)$ is a proper crossing or a defective noncrossing, then the relative orders of $(u_j, u_{j'})$ and $( (yu)_j, (yu)_{j'} )$ are different, i.e., $u_{j'} < u_j$. By the definition of $j, j'$ and (6.8) we also have $j' < j$. Thus, the pair of letters $( (yu)_j, (yu)_{j'} )$ is inverted in the word yu and not in the word ${\hat{y}}u$. It follows that $\ell (yu) > \ell ({\hat{y}}u)$ and by (6.13) that $\ell (y) > \ell ({\hat{y}}) = \ell (y) - 1$. The other case of (6.9) is similar.

To justify the identities (6.10) – (6.12), we first look closely at paths $\pi _i = {\hat{\pi }}_i$, $i \notin \{j, j'\}$, which pass through the interior vertex of $G_{J_p}$. We partition such paths into nine equivalence classes according to whether they enter $G_{J_p}$ below the both of the paths $\pi _{u_j}$, $\pi _{u_{j'}}$ (equivalently, below both ${\hat{\pi }}_{u_j}$, ${\hat{\pi }}_{u_{j'}}$) between the two paths, or above both paths, and whether they leave $G_{J_p}$ below, between, or above the two paths. We name the nine classes AD, AE, AF, BD, BE, BF, CD, CE, CF, according to the (magnified) diagrams of paths intersecting in $G_{J_p}$

(6.14)

The solid and dashed lines represent edges from $\pi _j$, $\pi _{j'}$, ${\hat{\pi }}_j$ and ${\hat{\pi }}_{j'}$, and the dotted lines the edges with highest and lowest sink or source indices among edges incident with the central vertex of $G_{J_p}$. Every other edge meeting this vertex lies in one of the six labeled regions. We may have $\pi _{u_j}$, $\pi _{u_{j'}}$ on the left, with ${\hat{\pi }}_{u_j}$, ${\hat{\pi }}_{u_{j'}}$ on the right, or vice versa. We may have the paths indexed by $u_j$ entering $G_{J_p}$ above the others in both diagrams, or below the others in both diagrams. All four combinations are possible. Thus, paths in class AE enter $G_{J_p}$ below the two bold paths and leave $G_{J_p}$ between them, while the class BE has cardinality b as defined in the statement of the lemma.

(Identity (6.10)) Consider the contributions of all points of intersection $(\pi _i, \pi _{i'}, k)$ and $({\hat{\pi }}_i, {\hat{\pi }}_{i'}, k)$ to $\textsc {cr}(\pi )$ and $\textsc {cr}({\hat{\pi }})$, respectively. For $k < p$ and all $i, i'$, we have that $(\pi _i, \pi _{i'}, k)$ is a crossing if and only if $({\hat{\pi }}_i, {\hat{\pi }}_{i'}, k)$ is a crossing. The same is true for $k \ge p$, provided that $i, i' \notin \{ u_j, u_{j'} \}$. For $k > p$ and $i \notin \{ u_j, u_{j'} \}$, crossings $(\pi _i, \pi _{u_j}, k)$ and $({\hat{\pi }}_i, {\hat{\pi }}_{u_{j'}}, k)$ correspond bijectively, as do crossings $(\pi _i, \pi _{u_{j'}}, k)$ and $({\hat{\pi }}_i, {\hat{\pi }}_{u_j}, k)$. By the definition of $j, j'$, there are no crossings of the form $(\pi _{u_j}, \pi _{u_{j'}}, k)$ or $({\hat{\pi }}_{u_j}, {\hat{\pi }}_{u_{j'}}, k)$ for $k > p$. So far, contributions to $\textsc {cr}(\pi )$ and $\textsc {cr}({\hat{\pi }})$ are equal.

Now consider points of intersection of the form

$$\begin{aligned} (\pi _i, \pi _{u_j}, p), \qquad (\pi _i, \pi _{u_{j'}}, p), \end{aligned}$$

(6.15)

for $i \notin \{ u_j, u_{j'} \}$, and their images under $\zeta$,

$$\begin{aligned} ({\hat{\pi }}_i, {\hat{\pi }}_{u_j}, p), \qquad ({\hat{\pi }}_i, {\hat{\pi }}_{u_{j'}}, p). \end{aligned}$$

(6.16)

If $\pi _i \in AF \cup CD$, then all four triples are crossings; if $\pi _i \in AD \cup CF$, then none is. If $\pi _i \in AE \cup BD \cup BF \cup CE$, then exactly one of the triples (6.15) is a crossing, as is exactly one of the triples (6.16). On the other hand, if $\pi _i$ is one of the b paths in BE, then either both triples (6.15) are crossings while both triples (6.16) are noncrossings (if $(\pi _{u_j}, \pi _{u_{j'}}, p)$ is a crossing), or both triples (6.15) are noncrossings while both triples (6.16) are crossings (if $(\pi _{u_j}, \pi _{u_{j'}}, p)$ is a noncrossing). Finally by the definition of $\zeta$, exactly one of the two triples

$$\begin{aligned} (\pi _{u_j}, \pi _{u_{j'}}, p), \qquad ({\hat{\pi }}_{u_j}, {\hat{\pi }}_{u_{j'}}, p) \end{aligned}$$

(6.17)

is a crossing and the other is a noncrossing. Thus, the points of intersection of the forms (6.15), (6.16), (6.17) contribute a surplus of $2b + 1$ to $\textsc {cr}(\pi )$ if $(\pi _{u_j}, \pi _{u_{j'}}, p)$ is a crossing, and to $\textsc {cr}({\hat{\pi }})$ otherwise.

(Identity (6.11)) For $k < p$ and all $i, i'$, we have that $(\pi _i, \pi _{i'}, k)$ is an inverted noncrossing if and only if $({\hat{\pi }}_i, {\hat{\pi }}_{i'}, k)$ is an inverted noncrossing. The same is true for $k \ge p$, provided that $i, i' \notin \{ u_j, u_{j'} \}$. For $k > p$ and $i \notin \{ u_j, u_{j'} \}$, noncrossings $(\pi _i, \pi _{u_j}, k)$ and $({\hat{\pi }}_i, {\hat{\pi }}_{u_{j'}}, k)$ correspond bijectively, as do noncrossings $(\pi _i, \pi _{u_{j'}}, k)$ and $({\hat{\pi }}_i, {\hat{\pi }}_{u_j}, k)$. Moreover, since paths indexed $u_j$, $u_{j'}$ all appear in the same column t, this correspondence preserves inversion of noncrossings. By the definition of $j, j'$, there are no noncrossings of the form $(\pi _{u_j}, \pi _{u_{j'}}, k)$ or $({\hat{\pi }}_{u_j}, {\hat{\pi }}_{u_{j'}}, k)$ for $k > p$. So far, contributions to $\textsc {invnc}(\pi )$ and $\textsc {invnc}({\hat{\pi }})$ are equal.

Now consider points of intersection of the forms (6.15), (6.16) for $i \notin \{ u_j, u_{j'} \}$. If $\pi _i \in AF \cup CD$, then all four triples are crossings; if $\pi _i \in AD \cup CF$, then all four are noncrossing. Moreover, if we have $\pi _i \in AD$ appearing to the left of column t or $\pi _i \in CF$ appearing to the right of column t, then all four noncrossings are inverted. Otherwise, none of the four is inverted. If $\pi _i \in AE \cup BD \cup BF \cup CE$, then exactly one of the triples (6.15) is a noncrossing, as is exactly one of the triples (6.16). These two noncrossings are inverted if we have $\pi _i \in AE \cup BD$ appearing to the right of column t, or if we have $\pi _i \in BF \cup CE$ appearing to the left of column t. Otherwise, the two noncrossings are not inverted. If $\pi _i \in BE$, then either both triples (6.15) are crossings while both triples (6.16) are not (if $(\pi _{u_j}, \pi _{u_{j'}}, p)$ is a crossing), or vice versa (if $(\pi _{u_j}, \pi _{u_{j'}}, p)$ is a noncrossing). In both cases, exactly one of the two noncrossings is inverted. Finally, observe that neither triple in (6.17) can be an inverted noncrossing, since all four paths appear in column t. Thus, the points of intersection of the forms (6.15), (6.16), (6.17) contribute a surplus of b to $\textsc {invnc}(\pi )$ if $(\pi _{u_j}, \pi _{u_{j'}}, p)$ is a crossing, and to $\textsc {cr}({\hat{\pi }})$ otherwise.

(Identity (6.12)) For $k < p$ and all $i, i'$, we have that $(\pi _i, \pi _{i'}, k)$ is a column defective noncrossing if and only if $({\hat{\pi }}_i, {\hat{\pi }}_{i'}, k)$ is a column defective noncrossing. The same is true for $k \ge p$, provided that $i, i' \notin \{ u_j, u_{j'} \}$. For $k > p$ and $i \notin \{ u_j, u_{j'} \}$, no triple $(\pi _i, \pi _{u_j}, k)$, $(\pi _i, \pi _{u_{j'}}, k)$, $({\hat{\pi }}_i, {\hat{\pi }}_{u_j}, k)$, $({\hat{\pi }}_i, {\hat{\pi }}_{u_{j'}}, k)$ can be a column defective noncrossing, since the definition of $j, j'$ guarantees that no path $\pi _i$ can belong to column t and intersect paths indexed by $u_j$, $u_{j'}$ to the right of $G_{J_p}$. So far, contributions to $\textsc {cdnc}(\pi )$ and $\textsc {cdnc}({\hat{\pi }})$ are equal.

Now consider points of intersection of the forms (6.15), (6.16) for $i \notin \{ u_j, u_{j'} \}$. If $\pi _i \in AF \cup BF \cup CF \cup AE \cup BE \cup CE$, then it cannot appear in column t by our choice of $j, j'$. If $\pi _i \in CD$, then all four triples are crossings. If $\pi _i \in AD \cup BD$, then $(\pi _i, \pi _{u_j}, p)$ is a column defective noncrossing if and only if $({\hat{\pi }}_i, {\hat{\pi }}_{u_j}, p)$ is, and $(\pi _i, \pi _{u_{j'}}, p)$ is a column defective noncrossing if and only if $({\hat{\pi }}_i, {\hat{\pi }}_{u_{j'}}, p)$ is. Finally, observe that neither triple in (6.17) can be a column defective noncrossing if $(\pi _{u_j}, \pi _{u_{j'}}, p)$ is proper, while exactly one of the two a column defective noncrossing if $(\pi _{u_j}, \pi _{u_{j'}}, p)$ is defective. Thus, the points of intersection of the forms (6.17) contribute a surplus of 1 to $\textsc {cdnc}(\pi )$ if $(\pi _{u_j}, \pi _{u_{j'}}, p)$ is a defective noncrossing, 1 to $\textsc {cdnc}({\hat{\pi }})$ if $(\pi _{u_j}, \pi _{u_{j'}}, p)$ is a defective crossing, and 0 to both otherwise. $\square$

As a consequence, we have that the map $\zeta$ preserves a certain linear combination of the above statistics.

Corollary 6.4

For $W = \delta (U(\pi , u, yu))$ and $\zeta (W) = \delta (U({\hat{\pi }}, u, {\hat{y}}u))$ in ${\mathcal {T}}_I$, we have

$$\begin{aligned}&\frac{\textsc {cr}({\hat{\pi }})}{2} + \textsc {cdnc}(\zeta (W)) + \textsc {invnc}(\zeta (W))\nonumber \\&\quad - \frac{\ell ({\hat{y}})}{2} = \frac{\textsc {cr}(\pi )}{2} + \textsc {cdnc}(W) + \textsc {invnc}(W) - \frac{\ell (y)}{2}. \end{aligned}$$

(6.18)

Proof

If W is a fixed point of $\zeta$, then the result is clear. Suppose therefore that $\zeta (W) \ne W$, and consider the triple $(\pi _{u_j}, \pi _{u_{j'}}, p)$ appearing in the definition of $\zeta$. If this triple is a proper noncrossing, then by Lemma 6.3 the left-hand side of (6.18) is

$$\begin{aligned}&\frac{\textsc {cr}(\pi ) + 1 + 2b}{2} + \textsc {cdnc}(W) + \textsc {invnc}(W) - b - \frac{\ell (y)+1}{2}\\&\quad = \frac{\textsc {cr}(\pi )}{2} + \textsc {cdnc}(W) + \textsc {invnc}(W) - \frac{\ell (y)}{2} + \frac{1 + 2b}{2} - b - \frac{1}{2}. \end{aligned}$$

One shows similarly that the result holds when the triple is a defective noncrossing or any crossing. $\square$

Finally, we can state and justify a subtraction-free formula for $\epsilon _q^\lambda ({\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q))$, generalizing [11, Thm. 5.4].

Theorem 6.5

Let $G = G_{J_1} \circ \cdots \circ G_{J_m}$. Then for $\lambda \vdash n$ we have

$$\begin{aligned} \epsilon _q^\lambda ({\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)) = \sum _\pi q^{\frac{\textsc {cr}(\pi )}{2}} \sum _W q^{\textsc {invnc}(W)}, \end{aligned}$$

(6.19)

where the sums are over path families $\pi$ of type e which cover G, and column-strict $\pi$-tableaux W of shape $\lambda ^{\, \top \,}$.

Proof

Let B be the path matrix of G. By Theorem 5.2 and Equations (2.12) – (2.13), the left-hand side of (6.19) is

$$\begin{aligned} \begin{aligned} \sigma _B(\mathrm {Imm}_{\epsilon _q^\lambda }(x))&= \sum _I \sigma _B(\mathrm {det}_q(x_{I_1,I_1}) \cdots \mathrm {det}_q(x_{I_r,I_r}))\\&= \sum _I \sum _{\smash {y \in {\mathfrak {S}}_\lambda }} (-1)^{\ell (y)}q^{\,\bar{\,}\frac{\ell (y)}{2}}\sigma _B (x^{u(I),yu(I)}), \end{aligned} \end{aligned}$$

(6.20)

where the first two sums are over ordered set partitions $I = (I_1,\dotsc ,I_r)$ of [n] of type $\lambda$. Fixing one such partition I and writing $u = u(I)$, we may use Proposition 4.5 and Lemma 6.1 to express the sum over $y \in {\mathfrak {S}}_\lambda$ as

$$\begin{aligned}&\sum _{y \in {\mathfrak {S}}_\lambda } \sum _\pi (-1)^{\ell (y)} q^{\,\bar{\,}\frac{\ell (y)}{2}}q^{\frac{\textsc {cr}(\pi )}{2}} q^{\textsc {invnc}(U(\pi ,u,yu))} \nonumber \\&\quad = \sum _{y \in {\mathfrak {S}}_\lambda } \sum _\pi (-1)^{\ell (y)} q^{\,\bar{\,}\frac{\ell (y)}{2}}q^{\frac{\textsc {cr}(\pi )}{2}} q^{\textsc {invnc}(W)+\textsc {cdnc}(W)}, \end{aligned}$$

(6.21)

where the inner sums are over path families $\pi$ of type $u^{-1}yu$ which cover G, and where $W = \delta _I(U(\pi ,u,yu))$. As y and $\pi$ vary in the above sums, $U(\pi ,u,yu)$ varies over all tableaux in ${\mathcal {U}}_I$, and W varies over all tableaux in ${\mathcal {T}}_I$.

Now consider a tableau $W \in {\mathcal {T}}_I$ which satisfies $\zeta (W) \ne W$. Let tableaux W and $\zeta (W)$ contain path families $\pi$ of type $u^{-1}yu$ and ${\hat{\pi }}$ of type $u^{-1}{\hat{y}}u$, respectively. Then the two terms on the right-hand side of (6.21) corresponding to $\zeta (W)$ and W sum to

$$\begin{aligned} (-1)^{\ell ({\hat{y}})} q^{\frac{\textsc {cr}({\hat{\pi }})}{2} + \textsc {invnc}(\zeta (W)) + \textsc {cdnc}(\zeta (W)) - \frac{\ell ({\hat{y}})}{2}} + (-1)^{\ell (y)} q^{\frac{\textsc {cr}(\pi )}{2} + \textsc {invnc}(W) + \textsc {cdnc}(W) - \frac{\ell (y)}{2}}. \end{aligned}$$

By Lemma 6.2 and Corollary 6.4 this is 0. Thus it suffices to sum the right-hand side of (6.21) over only the pairs $(y,\pi )$ corresponding to tableaux W satisfying $W = \zeta (W)$. By the definition of $\zeta$, each such tableau W is column-strict and, therefore, satisfies $\textsc {cdnc}(W) = 0$. Since all tableaux in ${\mathcal {T}}_I$ are also column-closed, each such tableau W must have type e. Thus, we have we have $u^{-1}yu = e$, i.e., $y=e$. It follows that the right-hand side of (6.21) and the third sum in (6.20) are equal to

$$\begin{aligned} q^{\frac{\textsc {cr}(\pi )}{2}} \sum _W q^{\textsc {invnc}(W)}, \end{aligned}$$

where the sum is over all tableau W in ${\mathcal {T}}_I$ which are column-strict of type e. Since all tableaux in ${\mathcal {T}}_I$ have shape $\lambda ^{\, \top \,}$, the three expressions in (6.20) are equal to the right-hand side of (6.19). $\square$

To illustrate the theorem, we compute $\epsilon _q^{211}({\widetilde{C}}_{s_{[1,2]}\,}(q) {\widetilde{C}}_{s_{[2,4]}\,}(q) {\widetilde{C}}_{s_{[1,2]}\,}(q))$ using the star network

(6.22)

There are two path families of type e which cover G, and four column-strict G-tableaux of shape $211^{\, \top \,}= 31$ for each

The path family $\pi$ has no crossings, and five noncrossings: $(\pi _3, \pi _4, 2)$, $(\pi _2, \pi _4, 2)$, $(\pi _2, \pi _3, 2)$, $(\pi _1, \pi _2, 1)$, $(\pi _1, \pi _2, 3)$. Checking for inverted noncrossings (higher path to the left of lower path) in each $\pi$-tableau, we have

	$U^{(1)}_\pi \,\,$	$U^{(2)}_\pi \,\,$	$U^{(3)}_\pi \,\,$	$U^{(4)}_\pi \,\,$
$(\pi _3, \pi _4, 2)$			$\,\text{ Inverted }\,$	$\,\text{ Inverted }\,$
$(\pi _2, \pi _4, 2)$		$\,\text{ Inverted }\,$	$\,\text{ Inverted }\,$	$\,\text{ Inverted }\,$
$(\pi _2, \pi _3, 2)$	$\,\text{ Inverted }\,$	$\,\text{ Inverted }\,$		$\,\text{ Inverted }\,$
$(\pi _1, \pi _2, 1)$
$(\pi _1, \pi _2, 3)$
$\,\textsc {invnc}(U^{(i)}_\pi )\,$	1	2	2	3

Thus, the $\pi$-tableaux contribute

$$\begin{aligned} q^{\frac{\textsc {cr}(\pi )}{2}} \sum _{i=1}^4 q^{\textsc {invnc}(U_\pi ^{(i)})} = q^{\frac{0}{2}}(q+q^2+q^2+q^3) = q+2q^2+q^3. \end{aligned}$$

(6.23)

The path family $\rho$ has two crossings, and three noncrossings: $(\rho _3, \rho _4, 2)$, $(\rho _1, \rho _4, 2)$, $(\rho _1, \rho _3, 2)$. Checking for inverted noncrossings in each $\rho$-tableau, we have

	$U^{(1)}_\rho \,\,$	$U^{(2)}_\rho \,\,$	$U^{(3)}_\rho \,\,$	$U^{(4)}_\rho \,\,$
$(\rho _3, \rho _4, 2)$			$\,\text{ Inverted }\,$	$\,\text{ Inverted }\,$
$(\rho _1, \rho _4, 2)$		$\,\text{ Inverted }\,$	$\,\text{ Inverted }\,$	$\,\text{ Inverted }\,$
$(\rho _1, \rho _3, 2)$	$\,\text{ Inverted }\,$	$\,\text{ Inverted }\,$		$\,\text{ Inverted }\,$
$\textsc {invnc}(U^{(i)}_\rho )$	1	2	2	3

Thus, the $\rho$-tableaux contribute

$$\begin{aligned} q^{\frac{\textsc {cr}(\rho )}{2}} \sum _{i=1}^4 q^{\textsc {invnc}(U_\rho ^{(i)})} = q^{\frac{2}{2}}(q+q^2+q^2+q^3) = q^2+2q^3+q^4, \end{aligned}$$

(6.24)

and we sum (6.23), (6.24) to obtain

$$\begin{aligned} \epsilon _q^{211}({\widetilde{C}}_{s_{[1,2]}\,}(q) {\widetilde{C}}_{s_{[2,4]}\,}(q) {\widetilde{C}}_{s_{[1,2]}\,}(q)) = q + 3q^2 + 3q^3 + q^4. \end{aligned}$$

It is interesting to note that the above example gives a combinatorial interpretation of the evaluation $\epsilon _q^{211}({\widetilde{C}}_{4231}(q))$ since

$$\begin{aligned} {\widetilde{C}}_{4231}(q) = {\widetilde{C}}_{s_{[1,2]}}(q) {\widetilde{C}}_{s_{[2,4]}}(q) {\widetilde{C}}_{s_{[1,2]}}(q). \end{aligned}$$

(6.25)

More generally, Theorem 6.5 allows one to combinatorially interpret evaluations of $\epsilon _q^\lambda$ at (multiples of) certain elements ${\widetilde{C}}_{w}(q)$ of the Kazhdan–Lusztig basis of $H_n(q)$: those which satisfy

$$\begin{aligned} g(q) {\widetilde{C}}_{w}(q) = {\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q) \end{aligned}$$

(6.26)

for some polynomial g(q) and some sequence $s_{J_1},\dotsc ,s_{J_m}$ of reversals. Such elements include ${\widetilde{C}}_{w}(q)$ for w belonging to the sets of

• (1) 321-hexagon-avoiding permutations [2, Thm. 1],

• (2) $3412$-avoiding, $4231$-avoiding permutations [19, Thm. 4.3],

• (3) ${\mathfrak {S}}_{4}$ (even 3412 which is 321-hexagon-avoiding, and 4231 by (6.25)),

• (4) ${\mathfrak {S}}_{5} \smallsetminus \{45312\}$.

Corollary 6.6

Suppose that ${\widetilde{C}}_{w}(q)$ has a factorization of the form (6.26) and define the star network $G = G_{J_1} \circ \cdots \circ G_{J_m}$. Then we have

$$\begin{aligned} \epsilon _q^\lambda ({\widetilde{C}}_{w}(q)) = \frac{1}{g(q)}\sum _\pi q^{\frac{\textsc {cr}(\pi )}{2}} \sum _W q^{\textsc {invnc}(W)}, \end{aligned}$$

(6.27)

where the sums are over path families $\pi$ of type e which cover G, and all column-strict G-tableaux W of shape $\lambda ^{\, \top \,}$.

It would be interesting to know for which Kazhdan–Lusztig basis elements we have the factorization (6.26) (see [19, Quest. 4.5]).

Recall from Eqs. (1.3)–(1.4) that Haiman’s result [10, Lem. 1.1] that we have

$$\begin{aligned} \chi _q^\lambda ({\widetilde{C}}_{w}(q)) \in {\mathbb {N}}[q] \end{aligned}$$

for all irreducible characters $\chi _q^\lambda$ and all $w \in {\mathfrak {S}}_n$ implies that we also have

$$\begin{aligned} \chi _q^\lambda ({\widetilde{C}}_{s_{J_1}\,}(q) \cdots {\widetilde{C}}_{s_{J_m}\,}(q)) \in {\mathbb {N}}[q] \end{aligned}$$

(6.28)

for all irreducible characters $\chi _q^\lambda$ and all sequences $(s_{J_1}, \dotsc , s_{J_m})$ of reversals. It would, therefore, be interesting to extend Theorem 6.5 to irreducible characters.

Problem 6.7

Find a combinatorial interpretation of the polynomial (6.28) which holds for all irreducible characters $\chi _q^\lambda$ and all sequences $(s_{J_1}, \dotsc , s_{J_m})$ of reversals.