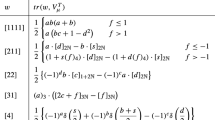Abstract
We define and study odd and even analogues of the major index statistics for the classical Weyl groups. More precisely, we show that the generating functions of these statistics, twisted by the one-dimensional characters of the corresponding groups, always factor in an explicit way. In particular, we obtain odd and even analogues of Carlitz’s identity, of the Gessel–Simion Theorem, and a parabolic extension, and refinement, of a result of Wachs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, a new statistic on the symmetric groups has been introduced and studied in relation with vector spaces over finite fields equipped with a certain quadratic form [21]. This statistic combines combinatorial and parity conditions and is now known as the odd inversion number, or odd length [10, 12]. Analogous statistics have later been defined and studied for the hyperoctahedral and even hyperoctahedral groups [11, 30, 31], and more recently for all Weyl groups [12]. A crucial property of this new statistic is that its signed (by length) generating function over the corresponding Weyl group always factors explicitly [12, 33].
Another line of research in the last 20 years has been the definition and study of analogues of the major index statistic for the other classical Weyl groups, namely for the hyperoctahedral and even hyperoctahedral groups (see, e.g., [1, 5, 7, 14,15,16, 24, 25, 32]) and for finite Coxeter groups [27]. It is now generally recognized that, among these, the ones with the best properties are those first defined by Adin and Roichman in [1] for the hyperoctahedral group and by Biagioli and Caselli in [7] for the even hyperoctahedral group.
Our purpose in this work is to define odd (and even) analogues of these major index statistics for the classical Weyl groups and show that their generating function twisted by the one-dimensional characters of the corresponding Weyl group always factors in an explicit way. More precisely, we show that certain multivariate refinements of these generating functions always factor explicitly. As consequences of our results we obtain odd and even analogues of Carlitz’s identity [13], which involves overpartitions, of the Gessel–Simion Theorem (see, e.g., [2, Theorem 1.3]), and of several other results appearing in the literature ([2, Theorems 5.1, 6.1, 6.2] and [6, Theorem 4.8]). We also obtain an extension, and refinement, of a result of Wachs ([34]).
The organization of the paper is as follows. In the next section, we recall some definitions and results that are used in the sequel. In Sect. 3, we define and study odd and even analogues of the major index and descent statistics of the symmetric group (Definition 3.1). In particular, we obtain odd and even analogues of Carlitz’s identity (Corollary 3.3), of the Gessel–Simion Theorem (Corollary 3.4), and a parabolic extension, and refinement, of a result of Wachs (Theorem 3.10). In Sect. 4, we define odd and even analogues of the major index statistics introduced in [1] and [7] for the classical Weyl groups of types B and D, respectively, and of the usual descent statistics on these groups (Definitions 4.1, 4.2 and 4.3). More precisely, we compute a multivariate refinement of the generating functions of these statistics twisted by the one-dimensional characters of the corresponding groups and show that they always factor explicitly. Finally, in Sect. 5, we show that, under some mild and natural hypotheses, there is no “odd major index” that is equidistributed with the odd length in the symmetric or hyperoctahedral groups and indicate some possible directions for future work.
2 Preliminaries
In this section, we recall some notation, definitions, and results that are used in the sequel. As \(\mathbb {N}\), we denote the set of non-negative integers and as \(\mathbb {P}\) the set of positive integers. If \(n\in \mathbb {N}\), then \([n]:=\{1,2,\ldots ,n\}\) and \([\pm n]:=\{-n,\ldots , -1,1,\ldots ,n\}\), in particular \([0]=\varnothing \). For \(n\in \mathbb {P}\), in the polynomial ring \(\mathbb {Z}[q]\) the q-analogue of n is defined by \([n]_q:=\sum \nolimits _{i=0}^{n-1}q^i\) and the q-factorial by \([n]_q!:=\prod \nolimits _{i=1}^n[i]_q\). We also find it convenient to let \( p_n := (1+(-1)^n)/2\). The cardinality of a set X is denoted by |X| and the power set of X by \(\mathcal {P}(X)\). For \(n,k \in {\mathbb {N}}\) we let \(\left( {\begin{array}{c}[n]\\ k\end{array}}\right) :=\{A\in \mathcal {P}([n]):|A|=k\}\).
For \(n\in \mathbb {N}\), \(i \in \mathbb {Z}\), \(q \in \mathbb {Q}\) and \(J \subseteq [n]\) we let \(J_e := \{j\in J:j\equiv 0{{\,\mathrm{(\mathrm {mod}~2)}\,}}\}\), \(J_o := \{j\in J:j\equiv 1{{\,\mathrm{(\mathrm {mod}~2)}\,}}\}\), \(J+i := \{i+j:j\in J\} \cap [n]\) and \(qJ := \{qj : j \in J\}\).
Next we recall some basic results in the theory of Coxeter groups which are useful in the sequel. The reader can consult [8] or [20] for further details. Let (W, S) be a Coxeter system. The length of an element \(z\in W\) with respect to S is denoted as \(\ell (z)\). If \(J\subseteq S\) and \(w \in W\) we let \(W^J:=\{w\in W:\ell (ws)>\ell (w)~\forall ~s\in J\}\), \(D(w):=\{s\in S:\ell (ws)<\ell (w)\}\) and, more generally, for any \(A\subseteq W\) we let \(A^J:=A\cap W^J\). When the group W is finite, there exists a unique element \(w_0\) of maximal length.
For any \(n\in \mathbb {P}\), let \(S_n\) be the group of bijections of the set [n]. For \(\sigma , \tau \in S_n\), we let \(\sigma \tau := \sigma \circ \tau \) (composition of functions). It is well known (see e.g. [8]) that this is a Coxeter group with set of generators \(\{s_1,s_2,\ldots ,s_{n-1}\}\), \(s_i\) being, in one line notation, \(12 \ldots (i+1)i \ldots n\), or in disjoint cycle notation \((i,i+1)\). Given a permutation \(\sigma = \sigma (1)\sigma (2)\ldots \sigma (n)\in S_n\), the action of \(s_i\) on the right is given by \(\sigma s_i = \sigma (1)\sigma (2)\ldots \sigma (i+1)\sigma (i)\ldots \sigma (n)\), for all \(i\in [n-1]\). As a Coxeter group, identifying \(\{s_1,s_2,\ldots ,s_{n-1}\}\) with \([n-1]\), we have the following well known result (see, e.g. [8]).
Proposition 2.1
Let \(\sigma \in S_{n}\). Then \( \ell (\sigma )=|\{(i,j) \in [n]^2 : i<j,\sigma (i)>\sigma (j)\}|, \) and \( D(\sigma )=\{i\in [n-1]:\sigma (i)>\sigma (i+1)\}. \)
So, given \(J \subseteq [n-1]\), \(S^J_n=\{\sigma \in S_n:\sigma (i)<\sigma (i+1)~\forall ~i \in J\}\).
For \(i \in [n]\) and \(T \subseteq S_n\) define \(T(i):=\{\sigma \in A: \sigma ^{-1}(n)=i\}\). For \(A \subseteq {\mathbb {Z}}\), \(A = \{ a_1, \ldots , a_k \}_<\) (so \(A = \{ a_1, \ldots , a_k \}\) and \(a_1< \cdots < a_k\)) and \(\sigma \in S(A)\) we let \(\tau \) be the only element of \(S_{|A|}\) defined by \(\sigma (a_i) = a_{\tau (i)}\) for all \(i \in [k]\). We call \(\tau \) the flattening of \(\sigma \) and write \(F(\sigma )=\tau \). Moreover, we define
for all \(i\in [\pm n]\), where \({{\,\mathrm{\mathrm {sgn}}\,}}(i):=1\) if \(i>0\) and \({{\,\mathrm{\mathrm {sgn}}\,}}(i):=-1\) if \(i<0\).
The elements of \(S_n^B\) are the bijective functions \(\sigma : [\pm n] \rightarrow [\pm n]\) satisfying \(-\sigma (i)=\sigma (-i)\), for all \(i\in [n]\). We use the window notation. So, for example, the element \([-2,1]\in S^B_2\) represents the function \(\sigma : [\pm 2] \rightarrow [\pm 2]\) such that \(\sigma (1)=-2=-\sigma (-1)\) and \(\sigma (2)=1=-\sigma (-2)\). We let \({{\,\mathrm{\mathrm {Neg}}\,}}(\sigma ):=\{i\in [n]:\sigma (i)<0\}\), \({{\,\mathrm{\mathrm {neg}}\,}}(\sigma )=|{{\,\mathrm{\mathrm {Neg}}\,}}(\sigma )|\), \(s^B_{j} :=(j,j+1)(-j,-j-1)\) for \(j=1,\ldots , n-1\), \(s_{0} :=(1,-1)\), and \(S_{B} :=\{ s_{0},s^B_1,\ldots ,s^B_{n-1} \}\). It is well known that \((S_{n}^{B},S_{B})\) is a Coxeter system of type \(B_{n}\) and that, identifying \(S_B\) with \([0,n-1]\), the following holds (see, e.g., [8, §8.1]). Given \(\sigma \in S^{B}_{n}\), we let
Proposition 2.2
Let \(\sigma \in {S_{n}^{B}}\). Then \(\ell _B(\sigma )=\ell _A(\sigma )-\sum \nolimits _{i\in {{\,\mathrm{\mathrm {Neg}}\,}}(\sigma )}\sigma (i)\), and \(D(\sigma )=\{i\in [0,n-1]:\sigma (i)>\sigma (i+1)\}\), where \(\sigma (0):=0\).
We let \(S^D_{n}\) be the subgroup of \(S^B_{n}\) defined by \( S^D_{n} :=\{ \sigma \in S^B_{n} : \, |{{\,\mathrm{\mathrm {Neg}}\,}}(\sigma )| \equiv 0 \pmod {2} \}, \) \(\tilde{s}_{0} :=(1,-2)(2,-1)\), and \(S_D :=\{ \tilde{s}_{0} ,s^B_{1},\ldots ,s^B_{n-1} \}\). It is then well known that \((S_{n}^{D},S_D)\) is a Coxeter system of type \(D_{n}\), and that the following holds (see, e.g., [8, §8.2]).
Proposition 2.3
Let \(\sigma \in {S_{n}^{D}}\). Then \(\ell _D(\sigma )=\ell _B(\sigma )-{{\,\mathrm{\mathrm {neg}}\,}}(\sigma )\), and \( D(\sigma )= \{ i \in [0,n-1] : \; \sigma (i)>\sigma (i+1) \} \) , where \(\sigma (0) :=-\sigma (2)\).
For simplicity, we often write \(B_n\) and \(D_n\), respectively, in place of \(S^B_n\) and \(S^D_n\). We refer to [8, Chapter 8] for further details on the combinatorics of the groups \(S^B_n\) and \(S^D_n\).
The descent number and the major index are the functions \({{\,\mathrm{des}\,}}: S_n \rightarrow \mathbb {N}\) and \({{\,\mathrm{\mathrm {maj}}\,}}: S_n \rightarrow \mathbb {N}\) defined, respectively, by \( {{\,\mathrm{des}\,}}(\sigma ):=|D(\sigma )|\), and \({{\,\mathrm{\mathrm {maj}}\,}}(\sigma ) :=\sum _{i \in D(\sigma )} i\), for all \(\sigma \in S_n\). More generally, we let \({{\,\mathrm{des}\,}}(a)=|D(a)|\) and \({{\,\mathrm{\mathrm {maj}}\,}}(a) :=\sum _{i \in D(a)} i\) for any sequence \(a=(a_1,\ldots ,a_n) \in \mathbb {Z}^n\), where \(D(a)=\{i\in [n-1]: a_i>a_{i+1}\}\).
Following [1] and [7], respectively, we define the flag-major index of an element \(\sigma \in S^B_n\) by
and the D-major index
where \(|\sigma |_n := [\sigma (1), \ldots , \sigma (n-1), |\sigma (n)|]\).
Recall that a one-dimensional character of a group G is a homomorphism \(\chi : G \rightarrow \mathbb {C}{\setminus }\{0\}\). The one-dimensional characters of \(S_n\) are well known to be the trivial and the alternating one, given by \(\sigma \mapsto 1\) and \(\sigma \mapsto (-1)^{\ell (\sigma )}\), respectively, for all \(\sigma \in S_n\). For the group \(S^B_n\), we have the following result (see [26, Proposition 3.1]):
Proposition 2.4
The hyperoctahedral group \(S_n^B\) has four one-dimensional characters, namely \(\sigma \mapsto 1\), \(\sigma \mapsto (-1)^{\ell (\sigma )}\), \(\sigma \mapsto (-1)^{{{\,\mathrm{\mathrm {neg}}\,}}(\sigma )}\) and \(\sigma \mapsto (-1)^{\ell (\sigma )+{{\,\mathrm{\mathrm {neg}}\,}}(\sigma )}\), for all \(\sigma \in S_n^B\).
The group \(S^D_n\) has only the trivial and the alternating one-dimensional characters \(\sigma \mapsto 1\) and \(\sigma \mapsto (-1)^{\ell (\sigma )}\), for all \(\sigma \in S^D_n\) ([26, Proposition 4.1]).
3 Type A
In this section, we introduce and study odd and even analogues of the descent and major index statistics for the symmetric groups. In particular, we obtain odd and even analogues of Carlitz’s identity, of the Gessel–Simion Theorem, and a parabolic extension, and refinement, of a result of Wachs.
Definition 3.1
We define functions \({{\,\mathrm{\mathrm {odes}}\,}},{{\,\mathrm{\mathrm {edes}}\,}},{{\,\mathrm{\mathrm {omaj}}\,}},{{\,\mathrm{\mathrm {emaj}}\,}}: S_n \rightarrow {\mathbb {N}}\) by letting
and
for all \(\sigma \in S_n\), where \(D(\sigma )_o = \{ i \in D(\sigma ) : i \equiv 1 \pmod {2} \}\) and \(D(\sigma )_e = \{ i \in D(\sigma ) : i \equiv 0 \pmod {2} \}\). We call these functions odd descent number, even descent number, odd major index, and even major index, respectively.
So for example, if \(\sigma =81725634\) then \({{\,\mathrm{\mathrm {odes}}\,}}(\sigma )=2\), \({{\,\mathrm{\mathrm {edes}}\,}}(\sigma )=1\), \({{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )=3\), and \({{\,\mathrm{\mathrm {emaj}}\,}}(\sigma )=3\).
For any \(J\subseteq [n-1]\) we let the parabolic q-Eulerian polynomials and parabolic signed q-Eulerian polynomials, respectively, be
and
So \(A^{\varnothing }_n(q,x)=A_n(q,x)\) and \(B^{\varnothing }_n(q,x)=B_n(q,x)\) where \(A_n(q,x)\) and \(B_n(q,x)\) are, respectively, the q-Eulerian polynomials and the signed q-Eulerian polynomials, as defined in [34].
Our goal is to compute the generating functions of odes, omaj, and of edes, emaj, twisted by the one-dimensional characters of the symmetric groups. Our first result is a natural trivariate generating function factorization.
Theorem 3.2
Let \(n\in \mathbb {P}\). Then
and
Proof
Let, for brevity, \(A^o_n(y,q,x) := \sum \limits _{\sigma \in S_n} y^{\ell (\sigma )} q^{{{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )} x^{{{\,\mathrm{\mathrm {odes}}\,}}(\sigma )}\). We prove the first equation by induction on \(n\geqslant 1\). We have that \(A^o_1(y,q,x)=1\), and \(A^o_2(y,q,x)=1+yxq\). So let \(n \ge 3\). For \(n\equiv 1 \pmod {2}\) we find, by our inductive hypothesis,
as desired. For \(n\equiv 0 \pmod {2}\) we have, by our inductive hypothesis,
as desired.
The proof for the even statistics is analogous, and is, therefore, omitted. \(\square \)
As a corollary of Theorem 3.2, we obtain the odd–even analogue of Carlitz’s identity [13]. Recall that an overpartition is a partition where the last occurrence of any number may be overlined (we refer the reader to [17]). So, for example, (1, 1, 1), \((1,1,\overline{1})\), (2, 1), \((\overline{2},1)\), \((2,\overline{1})\) and \((\overline{2},\overline{1})\) are the overpartitions of 3. We denote by \(\overline{{{\mathcal {P}}}}\) the set of overpartitions.
Corollary 3.3
Let \(n\in \mathbb {P}\). Then
and
Proof
By Theorem 3.2, we have that
and the result follows immediately. The proof of the second equation is identical. \(\square \)
Note that Corollary 3.3 can also be stated in terms of super-Schur functions. Given a partition \(\lambda \) and variables \(x_1,\ldots ,x_m,y_1,\ldots ,y_n\) we denote by \(s_{\lambda }(x_1,\ldots ,x_m/y_1,\ldots ,y_n)\) the super-Schur function (also known as hook Schur function, see [3]) associated to \(\lambda \) (we refer the reader to [28] for the definition and further information about super-Schur functions). Then we have, by [9, Equation (6)],
and
A second corollary of Theorem 3.2 is the odd–even analogue of the Gessel–Simion Theorem.
Corollary 3.4
Let \(n\in \mathbb {P}\). Then
and
A further corollary is the following.
Corollary 3.5
Let \(n\in \mathbb {P}\). Then \(\sum \nolimits _{\sigma \in S_n} q^{{{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )}\) and \(\sum \nolimits _{\sigma \in S_n} q^{{{\,\mathrm{\mathrm {emaj}}\,}}(\sigma )}\) are symmetric unimodal polynomials.
Proof
It follows immediately from Theorem 3.2 that \( \sum \nolimits _{\sigma \in S_n} q^{{{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )} =\frac{n !}{2^{\lfloor \frac{n}{2}\rfloor }} \prod _{i=1}^{\left\lfloor \frac{n}{2}\right\rfloor } (1+q^{i}), \) and that \( \sum \nolimits _{\sigma \in S_n} q^{{{\,\mathrm{\mathrm {emaj}}\,}}(\sigma )} = \frac{n !}{2^{\lfloor \frac{n-1}{2}\rfloor }} \prod _{i=1}^{\left\lfloor \frac{n-1}{2}\right\rfloor } (1+q^{i}). \) But it is well known (see, e.g., [29]) that the polynomial \(\prod \nolimits _{i=1}^{k} (1+q^{i})\) is unimodal for all \(k \ge 1\). \(\square \)
We note the following similar unimodality result.
Proposition 3.6
Let \(n,m \geqslant 1\). Then the polynomial \(\sum \nolimits _{\{\lambda \in \overline{{{\mathcal {P}}}}: \lambda _1\leqslant n, \ell (\lambda )=m\}} q^{|\lambda |}\) is symmetric and unimodal with center of symmetry at \(\frac{m(n+1)}{2}\).
Proof
Let \(P_{n,m}(q):=\sum \nolimits _{\{\lambda \in \overline{{{\mathcal {P}}}}: \lambda _1\leqslant n, \ell (\lambda )=m\}} q^{|\lambda |}\). It is easy to see that \(\deg (P_{n,m})=nm\) and that \(q^{(n+1)m}P_{n,m}(q^{-1})=P_{n,m}(q)\). Moreover,
where \(e_i\) are the elementary symmetric functions and \(h_i\) are the complete symmetric functions (see, e.g., [23, Chapter 1]). It is well known that \(e_i(1,q,\ldots ,q^{n-1})=q^{\left( {\begin{array}{c}i\\ 2\end{array}}\right) }\left( {\begin{array}{c}n\\ i\end{array}}\right) _q\), while \(h_{m-i}(1,q,\ldots ,q^{n-1})=\left( {\begin{array}{c}n+m-i-1\\ m-i\end{array}}\right) _q\) (see, e.g., [23, Example 1.3]) where \(\left( {\begin{array}{c}a\\ b\end{array}}\right) _q:= [a]_q!/([b]_q![a-b]_q)!\) is the q-binomial coefficient. Since \(\left( {\begin{array}{c}a\\ b\end{array}}\right) _q\) is a symmetric unimodal polynomial of degree \(b(a-b)\) (see, e.g., [29, Theorem 11]) and the product of two symmetric unimodal polynomials with nonnegative coefficients is again symmetric and unimodal (see, e.g. [29, Proposition 1]), we have that the product \(e_i(1,q,\ldots ,q^{n-1})h_{m-i}(1,q,\ldots ,q^{n-1})\) is symmetric and unimodal with center of symmetry \(\frac{m(n-1)}{2}\). Therefore, \(P_{n,m}(q)\) is symmetric and unimodal with center of symmetry \(\frac{m(n+1)}{2}\). \(\square \)
Note that Proposition 3.6 is related to, but different from, [18, Conjecture 7.2] namely that the polynomial \(\sum \nolimits _{\{\lambda \in \overline{{{\mathcal {P}}}}: \lambda _1\leqslant n, \ell (\lambda )\leqslant m\}}q^{|\lambda |}\) is unimodal.
Note that the parabolic analogues of the odd and even q-Eulerian polynomials do not factor nicely, in general. For example, one can check that \(\sum _{\sigma \in S^{\{2\}}_4} q^{{{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )}=5q^3 +3q^2 + 3q + 1\), and that \(\sum _{\sigma \in S^{\{1,3\}}_5} q^{{{\,\mathrm{\mathrm {emaj}}\,}}(\sigma )}=16q^3 + 4q^2 + 9q + 1\). Also, the bivariate generating function of \({{\,\mathrm{\mathrm {omaj}}\,}}\) and \({{\,\mathrm{\mathrm {emaj}}\,}}\) does not seem to factor. For example, \(\sum _{\sigma \in S_{3}} q_1^{{{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )} q_2^{{{\,\mathrm{\mathrm {emaj}}\,}}(\sigma )}=q_1 q_2 + 2q_1 + 2q_2 + 1\). The “signed” generating functions, however, can always be reduced to that over a certain subset, that of “Wachs permutations”, which we now define. Such generating functions, in turn, can often, though not always, be computed combinatorially, as we show in the sequel.
For \(n \in \mathbb {P}\), we define
So these are permutations where, in one line notation, 1 and 2, 3 and 4, etc. appear in adjacent positions. For example, \(21534 \in \mathcal {W}(S_5)\) while \(23541 \notin \mathcal {W}(S_5)\). For n even this class of permutations first appeared in [34] in the study of the signed Eulerian numbers. For this reason, we call the elements of \(\mathcal {W}(S_n)\) Wachs permutations.
Note that, if n is even, \(\mathcal {W}(S_n) = \{ \sigma \in S_n : | \sigma (i)-\sigma (i^{*})| \le 1 \; \text{ if } \;i \in [n-1] \}\).
Proposition 3.7
Let \(m>0\) and \(J \subseteq [2m-1]\). Then there is a bijection between \(\mathcal {W}(S_{2m}) \cap S_{2m}^J\) and \(S_m^{J_e/2} \times {{\mathcal {P}}}(\{ i \in [m] : 2i-1 \notin J \}) \).
Proof
For \(J=\varnothing \) the bijection is obtained by associating with each \(\sigma \in S_m\) and \(S \subseteq [m]\) the permutation \(u \in \mathcal {W}(S_{2m})\) defined by
and
for \(j \in [m]\). So, for example, if \(\sigma =4213\) and \(S=\{ 2,3 \} \) then \(u=78432156 \). If \(J \subseteq [2m-1]\) then the bijection just described restricts to a bijection between \(\mathcal {W}(S_{2m}) \cap S_{2m}^J\) and \( S_m^{J_e/2} \times {{\mathcal {P}}}(\{ i \in [m] : 2i-1 \notin J \})\). \(\square \)
In general, it is not hard to see that \(|\mathcal {W}(S_n)| = 2^{\left\lfloor \frac{n}{2} \right\rfloor } \left\lceil \frac{n}{2} \right\rceil !\). The previous bijection implies the following natural algebraic interpretation of \({{\,\mathrm{\mathrm {odes}}\,}}, {{\,\mathrm{\mathrm {edes}}\,}}\) and \({{\,\mathrm{\mathrm {omaj}}\,}}, {{\,\mathrm{\mathrm {emaj}}\,}}\) for Wachs permutation of even rank. The proof is a routine check, and is, therefore, omitted.
Lemma 3.8
Let \(m \in {\mathbb {P}}\), and \(u \in \mathcal {W}(S_{2m})\), \(u=(\sigma , S)\). Then
-
1.
\(\ell (u)=4\ell (\sigma ) + |S|\),
-
2.
\({{\,\mathrm{\mathrm {odes}}\,}}(u)=|S|\), \({{\,\mathrm{\mathrm {edes}}\,}}(u)={{\,\mathrm{des}\,}}(\sigma )\),
-
3.
\({{\,\mathrm{\mathrm {omaj}}\,}}(u)=\sum \limits _{t \in S}t\), \({{\,\mathrm{\mathrm {emaj}}\,}}(u)={{\,\mathrm{\mathrm {maj}}\,}}(\sigma )\).
The proposition below gives a sign-reversing involution that reduces the computation of the signed generating function over any quotient to the corresponding set of Wachs permutations.
Proposition 3.9
Let \(n \in \mathbb {P}\), and \(J \subseteq [n-1]\). Then
Proof
Let \(\sigma \in S_{n}^{J} {\setminus } \mathcal {W}(S_n)\) and \(r := \min \{ i \in [n-1] : | \sigma ^{-1}(i)-\sigma ^{-1}(i^{*})| \ge 2 \}\). Define the map \(\iota : S_{n}^{J} {\setminus } \mathcal {W}(S_n) \rightarrow S_{n}^{J} {\setminus } \mathcal {W}(S_n)\) by \(\iota (\sigma ):= (r, r^{*}) \, \sigma \), for all \(\sigma \in S_{n}^{J} {\setminus } \mathcal {W}(S_n)\). Then \( \ell (\iota (\sigma )) \equiv \ell (\sigma )+1 \pmod {2}\), \(D(\iota (\sigma )) =D(\sigma )\), and \(\iota (\iota (\sigma )) = \sigma \) for all \(\sigma \in S_n^J {\setminus } \mathcal {W}(S_n)\), so the result follows. \(\square \)
The following result is a refinement, and extension, of [34, Theorem 1] (which is the case \(J= \emptyset \), \(q_1=q_2=q^2\), \(x_1=x/q\) and \(x_2=x\)).
Theorem 3.10
Let \(m \in \mathbb {P}\), and \(J \subseteq [2m-1]\). Then
Proof
Let \(A:=\{ i \in [m] \, : \, 2i-1 \notin J \}\). Then by Lemma 3.8 and the considerations preceding it we have that
The result follows from Proposition 3.9. \(\square \)
We note the following consequences of Theorem 3.10.
Corollary 3.11
Let \(m\in \mathbb {P}\). Then
Note that for symmetric groups of odd rank the bivariate signed generating function of \({{\,\mathrm{\mathrm {omaj}}\,}}\) and \({{\,\mathrm{\mathrm {emaj}}\,}}\) does not factorize nicely. For example, \(\sum _{\sigma \in S_5} (-1)^{\ell (\sigma )}q_{1}^{{{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )} q_{2}^{{{\,\mathrm{\mathrm {emaj}}\,}}(\sigma )}=(1+y^2)(1+x^3+xy^4+x^4y^4-2x^3y^2-2xy^2)\).
Corollary 3.12
Let \(m\in \mathbb {P}\) and \(J\subseteq [2m-1]\). Then
Proof
This follows immediately by taking \(q_1=q_2=q^2\), \(x_1 = \frac{x}{q}\), and \(x_2=x\) in Theorem 3.10. \(\square \)
Corollary 3.13
Let \(m\in \mathbb {P}\). Then
We note that the previous “sign-balance” identities are examples of the phenomenon described in [19], namely that the signed enumeration on 2m objects by certain statistics is essentially equivalent to the ordinary enumeration on m objects by the same statistics.
4 Types B and D
In this section, we define and study odd and even analogues of the descent and flag-major statistics on the classical Weyl groups of types B and D, and compute the generating functions of these statistics twisted by the one-dimensional characters of these groups.
For \(i\in [n-1]\) we write, for brevity, “\(s_i\)” rather than “\(s^B_i\)”. We also define
for all \(i\in [n-1]\). Note that the involution of \(B_n\) defined by \(\sigma \mapsto s_i^*\sigma \), restricts to \(D_n\).
Definition 4.1
We define six statistics on the hyperoctahedral group \(B_n\) by letting
for all \(\sigma \in B_n\).
So, for example, if \(\sigma =[-2,5,3,1,-4]\) then \(D(\sigma )=\{ 0,2,3,4 \}\), \({{\,\mathrm{\mathrm {Neg}}\,}}(\sigma )=\{ 1,5 \}\), \({{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )=2\), \({{\,\mathrm{\mathrm {odes}}\,}}(\sigma )=1\), \({{\,\mathrm{\mathrm {oneg}}\,}}(\sigma )=2\), \({{\,\mathrm{\mathrm {emaj}}\,}}(\sigma )=3\), \({{\,\mathrm{\mathrm {edes}}\,}}(\sigma )=3\), and \({{\,\mathrm{\mathrm {eneg}}\,}}(\sigma )=0\). Note that, if \(\sigma \in S_n\), then the first four of these statistics coincide with those already defined in the previous section by the same name.
Definition 4.2
We define the odd flag-major index and the even flag-major index of \(\sigma \in B_n\) by letting
So, if \(\sigma \) is as above then \({{\,\mathrm{\mathrm {ofmaj}}\,}}(\sigma )={{\,\mathrm{\mathrm {efmaj}}\,}}(\sigma )=6\).
For \(\sigma \in B_n\) we let \(|\sigma |_n := [\sigma (1), \ldots , \sigma (n-1), |\sigma (n)|]\). We then define six more statistics on \(B_n\).
Definition 4.3
We let
for all \(\sigma \in B_n\).
So, for example, if \(\sigma \) is as above then \({{\,\mathrm{\mathrm {odes}}\,}}_D(\sigma )=1\), \({{\,\mathrm{\mathrm {oDmaj}}\,}}(\sigma )=5\), \({{\,\mathrm{\mathrm {edes}}\,}}_D(\sigma )=2\) and \({{\,\mathrm{\mathrm {eDmaj}}\,}}(\sigma )=2\). We call \({{\,\mathrm{\mathrm {oDmaj}}\,}}\) and \({{\,\mathrm{\mathrm {eDmaj}}\,}}\) the odd D-major index and the even D-major index of \(\sigma \in B_n\), respectively.
Our aim is to compute the generating functions \( \sum \nolimits _{\sigma \in B_n} \chi (\sigma ) x^{{{\,\mathrm{\mathrm {ofmaj}}\,}}(\sigma )} y^{{{\,\mathrm{\mathrm {odes}}\,}}(\sigma )} z^{{{\,\mathrm{\mathrm {oneg}}\,}}(\sigma )}\) and \( \sum \nolimits _{\sigma \in D_n} \chi (\sigma ) x^{{{\,\mathrm{\mathrm {oDmaj}}\,}}(\sigma )} y^{{{\,\mathrm{\mathrm {odes}}\,}}_D(\sigma )} z^{{{\,\mathrm{\mathrm {oneg}}\,}}_D(\sigma )}\) where \(\chi \) is any one-dimensional character of the corresponding group, and the analogous even ones.
4.1 The Trivial Character
We start with the trivial characters of \(B_n\) and \(D_n\). Recall that we let \( p_n := (1+(-1)^n)/2\).
Theorem 4.4
Let \(n \ge 2\). Then
and
Proof
We only prove the formula for the odd statistics, the proof for the even ones being analogous. We proceed by induction on \(n \ge 2\), the result being easy to check for \(n=2\). Suppose first that n is odd. Then we have that
as desired. Suppose now that n is even. Let \(\sigma \in B_n\) and \([\tau ,i,j]\) be its window notation (\(i,j \in [\pm n]\)). Then one can check that
Therefore, we conclude that
and the result again follows. \(\square \)
The corresponding result for \(D_n\) is a consequence of the one in type B. Note that if \(f_1,\ldots ,f_k : B_n \rightarrow \mathbb {N}\) then
Theorem 4.5
Let \(n \geqslant 3\). Then
and
Proof
Let \(n \ge 3\) be odd. Then
and the result follows from Theorem 4.4 and (1). Let now n be even. Let \(\sigma \in B_n\) and \([\tau ,i,j]\) be its window notation (\(i,j \in [\pm n]\)). Then we have that
Therefore,
and the result again follows from Theorem 4.4 and (1).
The proof for the even statistics is analogous and is, therefore, omitted. \(\square \)
4.2 The Alternating Character
The computation for the character \(\sigma \mapsto (-1)^{\ell _B(\sigma )}\) of \(S^B_n\) is considerably more involved. We begin with the following reduction result. For \(n \in {\mathbb {P}}\), we let
We call the elements of \(\mathcal {W}(B_n)\) signed Wachs permutations. So, for example, \([-3,-4,5,2,1] \in \mathcal {W}(B_5)\) while \( [3,-4,1,2] \notin \mathcal {W}(B_4)\).
Proposition 4.6
Let \(n \in {\mathbb {P}}\), and \(S \subseteq [n]\). Then
Proof
Let \(\widehat{B_n} :=\{ \sigma \in B_n : {{\,\mathrm{\mathrm {Neg}}\,}}(\sigma )=S \}\), and \(\varphi : \widehat{B_n} {\setminus } \mathcal {W}(B_n) \rightarrow \widehat{B_n} {\setminus } \mathcal {W}(B_n)\) be defined by \(\varphi (\sigma ):= s_r^*\sigma \), where \(r:= \min \{ i \in [n-1] : |\sigma ^{-1}(i) - \sigma ^{-1}(i^{*}) | \ge 2 \}\) if \(\sigma \in \widehat{B_n} {\setminus } \mathcal {W}(B_n)\). Then \(\varphi : \widehat{B_n} {\setminus } \mathcal {W}(B_n) \rightarrow \widehat{B_n} {\setminus } \mathcal {W}(B_n)\) is an involution, \(\ell _B( \varphi (\sigma )) \equiv \ell _B(\sigma ) +1 \pmod {2}\), and \(D(\varphi (\sigma ))=D(\sigma )\), so the result follows. \(\square \)
Note that there is a bijection between \(\mathcal {W}(B_{2m})\) and \(B_m \times {{\mathcal {P}}}([m])\) obtained by associating with each \(\sigma \in B_m\) and \(S \subseteq [m]\) the signed permutation \(u \in B_{2m}\) defined by
for \(j \in [m]\). So, for example, if \(\sigma =[3,-1,-2,5,-4]\) and \(S = \{ 1,4,5 \}\) then \(u=[6,5,-2,-1,-4,-3,10,9,-7,-8]\). Because of this bijection we will often identify \(\mathcal {W}(B_{2m})\) and \(B_m \times {{\mathcal {P}}}([m])\) and write simply \(u=(\sigma , S)\) to mean that u and \((\sigma , S)\) correspond under this bijection. The proof of the next result is a routine check using our definitions, and is, therefore, omitted.
Lemma 4.7
Let \(m \in {\mathbb {P}}\), and \(u \in \mathcal {W}(B_{2m})\), \(u=(\sigma , S)\). Then
-
1.
\({{\,\mathrm{\mathrm {neg}}\,}}(u)=2 {{\,\mathrm{\mathrm {neg}}\,}}(\sigma )\), \({{\,\mathrm{\mathrm {oneg}}\,}}(u)={{\,\mathrm{\mathrm {eneg}}\,}}(u)={{\,\mathrm{\mathrm {neg}}\,}}(\sigma )\);
-
2.
\({{\,\mathrm{\mathrm {odes}}\,}}(u)=|S|\), \({{\,\mathrm{\mathrm {edes}}\,}}(u)={{\,\mathrm{des}\,}}(\sigma )\);
-
3.
\({{\,\mathrm{\mathrm {omaj}}\,}}(u)=\sum _{t \in S} t\), \({{\,\mathrm{\mathrm {emaj}}\,}}(u)={{\,\mathrm{\mathrm {maj}}\,}}(\sigma )\);
-
4.
\(\ell _A(u)=4 \ell _A(\sigma ) + |S|\) and \(\ell _B(u)=4 \ell _B(\sigma ) + |S|- {{\,\mathrm{\mathrm {neg}}\,}}(\sigma )\).
For brevity, we define the following two monomials, for any \(\sigma \in B_n\): \( \sigma _o(x,y):=x^{{{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )} y^{{{\,\mathrm{\mathrm {odes}}\,}}(\sigma )}\) and \(\sigma _e(x,y):=x^{{{\,\mathrm{\mathrm {emaj}}\,}}(\sigma )} y^{{{\,\mathrm{\mathrm {edes}}\,}}(\sigma )}\). We need to prove a further reduction result.
Lemma 4.8
Let \(m \in {\mathbb {P}}\), and \(S \subseteq [2m+1]\). Then
and
Proof
Let \(\psi : \{ \sigma \in B_{2m+1} : |\sigma (2m+1)| \ne 2m+1 \} \rightarrow \{ \sigma \in B_{2m+1} : |\sigma (2m+1)| \ne 2m+1 \}\) be defined by \(\psi (\sigma ):= s_r^* \sigma \) where \(r:= \sigma (2m+1)\). Then \(\psi \) is an involution, \(\ell _B( \psi (\sigma )) \equiv \ell _B(\sigma ) +1 \pmod {2}\), \({{\,\mathrm{\mathrm {Neg}}\,}}(\psi (\sigma ))={{\,\mathrm{\mathrm {Neg}}\,}}(\sigma )\) and \(D(\sigma )_o=D(\psi (\sigma ))_o\). This proves the first equation. The proof for the even one is analogous and is therefore omitted. \(\square \)
For \(S\subseteq [n]\) we define \(S^*:=\{i^*:i \in S\}\). Using the reductions proved so far we can now compute explicitly several “building blocks” of the generating functions that we are interested in.
Lemma 4.9
Let \(m \in {\mathbb {P}}\), and \(S \subseteq [2m]\). Then
and
Proof
Note that, by Proposition 4.6,
and the right-hand side is zero whenever \(S\ne S^*\). If \(S=S^*\), by Lemma 4.7, we have that
as claimed.
For the even statistics, note that the assignment \(\sigma \mapsto s_{|\sigma (1)|}^*\sigma \) defines an involution of \(B_{2m}\) which preserves the functions \({{\,\mathrm{\mathrm {emaj}}\,}}\) and \({{\,\mathrm{\mathrm {edes}}\,}}\), so the result follows. \(\square \)
Lemma 4.10
Let \(m\in \mathbb {P}\) and \(S \subseteq [2m+1]\). Then
Proof
Let \(1\in S\). Then \(0 \in D(\sigma )\) for all \(\sigma \in B_n\) such that \({{\,\mathrm{\mathrm {Neg}}\,}}(\sigma )=S\). We have that, by Lemma 4.8,
and the result follows by Lemma 4.9. If \(1\not \in S\) the result follows by analogous computations. \(\square \)
Note that if |S| is even (resp., odd) the first (resp., second) case in the above lemma cannot occur. We can now prove one of our main results. Recall that we have defined \(p_n:=\frac{1+(-1)^n}{2}\).
Theorem 4.11
Let \(n \geqslant 2\). Then
where \(\epsilon \in \{0,1\}\) and \(\mathcal {O}_n(x,y,z_1,z_2):=\left\lfloor \frac{n}{2} \right\rfloor ! (1-z_1 z_2)^{\left\lfloor \frac{n-1}{2} \right\rfloor } \prod _{i=1}^{\left\lfloor \frac{n}{2} \right\rfloor } (1-yx^i)\).
Proof
We write \(\sigma _o(x,y,z_1,z_2):=x^{{{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )} y^{{{\,\mathrm{\mathrm {odes}}\,}}(\sigma )}z_1^{{{\,\mathrm{\mathrm {oneg}}\,}}(\sigma )} z_2^{{{\,\mathrm{\mathrm {eneg}}\,}}(\sigma )}\) for brevity and we begin by proving (2) for \(\epsilon =1\). Note that
This already proves (2) if \(\epsilon =1\) and n is even, by Lemma 4.9. Suppose now that n is odd. Then for all \(S \subseteq [n-1]\) such that \(|S| \equiv 1 \pmod {2}\) we have that, by Lemmas 4.8 and 4.9,
and (2) for \(\epsilon =1\) again follows.
We now prove (2) for \(\epsilon =0\). Suppose first that n is even. Then proceeding as in the previous case and using Lemma 4.9, we have that
and (2) follows in this case. If n is odd then by Lemma 4.8, we have similarly that
by Lemma 4.9 and (2) again follows.
We now prove (3) for \(\epsilon =1\). We have that
and this proves (3) in this case by Lemma 4.9 if n is even. Suppose now that n is odd. Then, from the previous equation and Lemmas 4.8 and 4.9, we have that
and (3) follows if \(\epsilon =1\).
Finally, if n is even, then we obtain similarly that
and (3) follows for \(\epsilon =0\). If n is odd then, by Lemmas 4.8 and 4.9
This proves (3) for \(\epsilon =0\) and this concludes the proof. \(\square \)
The following is the even analogue of the previous theorem. Its proof is similar and is, therefore, omitted.
Theorem 4.12
Let \(n\geqslant 2\). Then
As a consequence of Theorems 4.11 and 4.12, we can now easily obtain the generating function of the odd flag-major index, the odd descent number, and the odd negative number, twisted by the alternating character of the hyperoctahedral group, and the corresponding even ones. For \(y=z=1\) this result is the odd and even analogue of [2, Theorem 5.1].
Corollary 4.13
Let \(n \geqslant 2\). Then
and
We note that Corollary 4.13 implies that
which is also implied by [26, Theorem 3.2].
Note that \(\sum _{\sigma \in B_{n}} (-1)^{\ell _B (\sigma )} x_{1}^{{{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )} x_{2}^{{{\,\mathrm{\mathrm {emaj}}\,}}(\sigma )}\) does not factor nicely, in general, for example, if \(n=5\) then one obtains \((1-x_1)(1-x_1x_2)^2(1+x_2^2)(x_1^6x_2^4 - 2x_1^4x_2^2 + x_1^2x_2^4 + x_1^4 - 2x_1^2x_2^2 + 1)\). Similarly \(\sum _{\sigma \in B_{n}} x^{\ell _B (\sigma )} y^{{{\,\mathrm{\mathrm {ofmaj}}\,}}(\sigma )}\) does not factor nicely. For example \(\sum _{\sigma \in B_{3}} x^{\ell _B (\sigma )} y^{{{\,\mathrm{\mathrm {ofmaj}}\,}}(\sigma )}=(x^2 + x + 1)(x^3y + 1)(x^4y^3 + x^3y^2 + x^3y + x^2y^2 + x^2y + xy^2 + xy + 1)\). Similar considerations hold in the even case.
As another simple consequence of Theorems 4.11 and 4.12, we also obtain the generating function of \({{\,\mathrm{\mathrm {oDmaj}}\,}}\), \({{\,\mathrm{\mathrm {odes}}\,}}_D\) and \({{\,\mathrm{\mathrm {oneg}}\,}}_D\), and the corresponding even one for the only non-trivial one-dimensional character of the even hyperoctahedral group. A special case of the following result (\(y=z=1\)) is the odd and even analogue of [6, Theorem 4.8].
Corollary 4.14
Let \(n \geqslant 2\). Then
and
Proof
For \(\sigma \in D_n\) let \(\tilde{\sigma } :=[\sigma (1), \ldots , \sigma (n-1), -\sigma (n)]\). Then we have from our definitions, Proposition 2.3 and Theorem 4.11 that
The second equation follows similarly from Theorem 4.12. \(\square \)
We note that, as in the case of the hyperoctahedral group, \(\sum \nolimits _{\sigma \in D_n}(-1)^{\ell _D(\sigma )}x_1^{{{\,\mathrm{\mathrm {oDmaj}}\,}}(\sigma )}x_2^{{{\,\mathrm{\mathrm {eDmaj}}\,}}(\sigma )}\) does not seem to factor, in general.
4.3 The Other Characters
We conclude by computing the generating function of the statistics studied in this section twisted by the remaining one-dimensional characters of the hyperoctahedral group.
As in the case of the alternating character, the following corollary can be deduced directly from Theorems 4.11 and 4.12. For \(y=z=1\), it is the odd and even analogue of [2, Theorem 6.1].
Corollary 4.15
Let \(n \geqslant 2\). Then
and
One can check that \(\sum _{\sigma \in B_{n}} (-1)^{\ell _B (\sigma )+{{\,\mathrm{\mathrm {neg}}\,}}(\sigma )} x_{1}^{{{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )} x_{2}^{{{\,\mathrm{\mathrm {emaj}}\,}}(\sigma )}\) does not factor explicitly in general.
To calculate the generating function of the statistics studied in this section twisted by the remaining character, we begin with a reduction result.
For \(\sigma \in B_n\) we let \(|\sigma | := [|\sigma (1)|, \ldots , |\sigma (n)|]\).
Proposition 4.16
Let \(n\geqslant 2\) and \(S\subseteq [n]\). Then
and
Proof
Let \(\sigma \in B_n\) and \(i\in [n-1]\) be such that \(i\equiv 1{{\,\mathrm{(\mathrm {mod}~2)}\,}}\) and \(|\sigma (i)|>|\sigma (i+1)|\). Let \(\tilde{\sigma }:= [\sigma (1),\ldots ,\sigma (i),-\sigma (i+1),\sigma (i+2),\ldots ,\sigma (n)]\). Then \({{\,\mathrm{\mathrm {neg}}\,}}(\tilde{\sigma })\equiv {{\,\mathrm{\mathrm {neg}}\,}}(\sigma )+1 {{\,\mathrm{(\mathrm {mod}~2)}\,}}\), \({{\,\mathrm{\mathrm {oneg}}\,}}(\tilde{\sigma })\!=\!{{\,\mathrm{\mathrm {oneg}}\,}}(\sigma )\), \({{\,\mathrm{\mathrm {odes}}\,}}(\tilde{\sigma })\!=\!{{\,\mathrm{\mathrm {odes}}\,}}(\sigma )\) and hence \({{\,\mathrm{\mathrm {omaj}}\,}}(\tilde{\sigma })={{\,\mathrm{\mathrm {omaj}}\,}}(\sigma )\).
The second formula is proved analogously. \(\square \)
The next result completes the computation of the generating functions of the statistics \({{\,\mathrm{\mathrm {ofmaj}}\,}}\), \({{\,\mathrm{\mathrm {odes}}\,}}\), and \({{\,\mathrm{\mathrm {oneg}}\,}}\), and their even counterparts, twisted by the one-dimensional characters of \(B_n\). For \(y=z=1\) the result is the odd and even analogue of [2, Theorem 6.2].
Theorem 4.17
Let \(n\geqslant 2\). Then
and
Proof
By Proposition 4.16 we have that
Now notice that, if \(\sigma \in B_n\) is such that \({{\,\mathrm{\mathrm {odes}}\,}}(|\sigma |)=0\) and \(i \equiv 1 {{\,\mathrm{(\mathrm {mod}~2)}\,}}\), then \(\sigma (i)>\sigma (i+1)\) if and only if \(\sigma (i+1)<0\), so \(D(\sigma )_o+1={{\,\mathrm{\mathrm {Neg}}\,}}(\sigma )_e\). Therefore the previous sum equals
The second equality follows analogously, using the reduction of Proposition 4.16. \(\square \)
The joint distribution of \({{\,\mathrm{\mathrm {ofmaj}}\,}}\) and \({{\,\mathrm{\mathrm {efmaj}}\,}}\) twisted by “negative” character does not seem to factor.
5 Final Comments
It is clear that the most desirable property that one would like an “odd major index” to possess is that it is equidistributed with the odd length. It is easy to see that, if we require, as seems reasonable, such an odd major index to be an additive function of the descent set, such an odd major index does not exist in general. For example, one has that
and one can check that there are no \(j_1,j_2,j_3,j_4 \in {\mathbb {N}}\) such that
where \(L(\pi ) := |\{ (i,j) \in [n]^2 : i<j, \pi (i) > \pi (j), i \not \equiv j \pmod {2} \} |\) is the odd length of the symmetric group. Of course this computation does not rule out the existence of more general odd and even major indexes such as, for example, polynomial functions with integer coefficients of the elements of the descent set.
Similar computations show that no additive “odd major index” that depends only on the descent and negative sets exists in the hyperoctahedral groups that is equidistributed with the odd length, where the odd length is the one defined in [30] and [31], and further studied in [10, 12], and [22], namely
where \(\sigma \in B_n\) and \(\sigma (0):=0\). Analogous considerations about more general indexes, as at the end of the previous paragraph, also apply in this case.
It is well known that major indexes possess remarkable algebraic interpretations in terms of coinvariant algebras and tensor invariant algebras (see, e.g. [1, 4] and [7]). It would be interesting to find similar interpretations for the odd and even statistics introduced and studied in this work. Moreover, considering that the flag-major index was originally defined in [1] for wreath products, a reasonable directions for further work would be to define and study odd and even analogues of these major indices for wreath products.
References
R. M. Adin and Y. Roichman, The flag major index and group actions on polynomial rings, Europ. J. Combin. 22, 431–446 (2001).
R. Adin, I. Gessel, and Y. Roichman, Signed Mahonians, J. Comb. Theory Series A, 109, 25–43 (2005).
A. Berele and A. Regev, Hook Young diagrams with applications to combinatorics and to representations of Lie superalgebras, Advances in Math., 64, 118–175 (1987).
F. Bergeron, Algebraic combinatorics and coinvariant spaces, CRC Press, 2009.
R. Biagioli, Major and descent statistics for the even-signed permutation group, Adv. in Appl. Math., 31(1), 163–179 (2003).
R. Biagioli, Signed Mahonian polynomials for classical Weyl groups, Europ. J. Combin. 27.2, 207–217 (2006).
R. Biagioli and F. Caselli, Invariant algebras and major indices for classical Weyl groups, Proceedings of the LMS 88.3, 603–631 (2004).
A. Björner, F. Brenti, Combinatorics of Coxeter Groups, Graduate Texts in Mathematics, 231, Springer-Verlag, New York, 2005.
F. Brenti, Determinants of Super-Schur Functions, Lattice Paths, and Dotted Plane Partitions, Advances in Math., 98, 27–64 (1993).
F. Brenti, A. Carnevale, Proof of a conjecture of Klopsch-Voll on Weyl groups of type\(A\), Trans. Amer. Math. Soc. 369, 7531–7547 (2017).
F. Brenti, A. Carnevale, Odd length for even hyperoctahedral groups and signed generating functions, Discrete Math., 340, 2822–2833 (2017).
F. Brenti, A. Carnevale, Odd length in Weyl groups, Algebraic Comb., 2, 1125–1147 (2019).
L. Carlitz, A combinatorial property of q-Eulerian numbers, Amer. Math. Monthly 82, 51–54 (1975).
R. J. Clarke and D. Foata, Eulerian calculus. I. Univariable statistics, Europ. J. Combin., 15 345–362, (1994).
R. J. Clarke and D. Foata, Eulerian calculus. II. An extension of Han’s fundamental transformation, Europ. J. Combin., 16, 221–252 (1995).
R. J. Clarke and D. Foata, Eulerian calculus. III. The ubiquitous Cauchy formula, Europ. J. Combin., 16 329–355, (1995).
S. Corteel and J. Lovejoy, Overpartitions, Trans. Amer. Math. Soc. 356.4, 1623–1635 (2004).
J. Dousse and K. Byungchan, An overpartition analogue of q-binomial coefficients, II: Combinatorial proofs and (q, t)-log concavity, J. Comb. Theory Series A 158, 228–253 (2018).
S. P. Eu, T. S. Fu, Y. J. Pan and C. T. Ting Two refined major-balance identities on\(321\)-avoiding involutions, Europ. J. Combin. 49, 250–264 (2015).
J. E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge Studies in Advanced Mathematics, no.29, Cambridge Univ. Press, Cambridge, 1990.
B. Klopsch, C. Voll, Igusa-type functions associated to finite formed spaces and their functional equations, Trans. Amer. Math. Soc., 361 no. 8, 4405–4436, (2009).
A. Landesman, Proof of Stasinski and Voll’s hyperoctahedral group conjecture, Australas. J. Combin., 71 196–240, (2018).
I. G. Macdonald, Symmetric functions and Hall polynomials, Oxford university press, 1998.
V. Reiner, Signed permutation statistics, Europ. J. Combin., 14 553–567, (1993).
V. Reiner, Signed permutation statistics and cycle type, Europ. J. Combin., 14 569–579, (1993).
V. Reiner, Descents and one-dimensional characters for classical Weyl groups, Discrete Math. 140.1–3, 129–140 (1995).
P. Sentinelli, Parabolically induced functions and equidistributed pairs, Boletín de la Sociedad Matemática Mexicana, 25 (3), 461–479 (2019).
R. Stanley, Unimodality and Lie Superalgebras, Studies in Appl. Math. 72, 263–281 (1985).
R. Stanley, Log-concave and unimodal sequences in Algebra, Combinatorics and Geometry, Annals of the New York Academy of Sciences, 576 500–534, (1989).
A. Stasinski, C. Voll, A new statistic on the hyperoctahedral groups, Electronic J. Combin., 20, no. 3, Paper 50, 23 pp. (2013).
A. Stasinski, C. Voll, Representation zeta functions of nilpotent groups and generating functions for Weyl groups of type B, Amer. J. Math., 136 (2) 501–550, (2014).
E. Steingrimsson, Permutation statistics of indexed permutations, Europ. J. Combin., 15, 187–205, (1994).
J. Stembridge, Sign-twisted Poincaré series and odd inversions in Weyl groups, Algebraic Comb., 2, no. 4, 621–644 (2019).
M. L. Wachs, An involution for signed Eulerian numbers, Discrete Math. 99.1–3, 59–62 (1992).
Acknowledgements
The first author would like to thank Sylvie Corteel for useful and interesting conversations that led to the proof of Proposition 3.6. This material is partly based upon work supported by the Swedish Research Council under grant no. 2016-06596 while the first author was in residence at Institut Mittag-Leffler in Djursholm, Sweden, during Spring 2020. The first author is partially supported by the MIUR Excellence Department Project CUP E83C18000100006. We also thank the referee for careful reading and useful comments.
Funding
Open access funding provided by Università degli Studi di Roma Tor Vergata within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Brenti, F., Sentinelli, P. Odd and Even Major Indices and One-Dimensional Characters for Classical Weyl Groups. Ann. Comb. 24, 809–835 (2020). https://doi.org/10.1007/s00026-020-00515-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00026-020-00515-2