Skip to main content
SpringerLink
Log in

On the Metric Dimension of Imprimitive Distance-Regular Graphs

  • Published:
Annals of Combinatorics Aims and scope Submit manuscript

Abstract

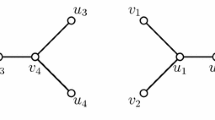
A resolving set for a graph \({\Gamma}\) is a collection of vertices S, chosen so that for each vertex v, the list of distances from v to the members of S uniquely specifies v. The metric dimension of \({\Gamma}\) is the smallest size of a resolving set for \({\Gamma}\). Much attention has been paid to the metric dimension of distance-regular graphs. Work of Babai from the early 1980s yields general bounds on the metric dimension of primitive distance-regular graphs in terms of their parameters. We show how the metric dimension of an imprimitive distance-regular graph can be related to that of its halved and folded graphs. We also consider infinite families (including Taylor graphs and the incidence graphs of certain symmetric designs) where more precise results are possible.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aldred R.E.L., Godsil C.D.: Distance-regular antipodal covering graphs. J. Combin. Theory Ser. B 45(2), 127–134 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  2. Alfuraidan M.R., Hall J.I.: Smith’s theorem and a characterization of the 6-cube as distance-transitive graph. J. Algebraic Combin. 24(2), 195–207 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  3. Babai L.: On the complexity of canonical labeling of strongly regular graphs. SIAM J. Comput. 9(1), 212–216 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  4. Babai L.: On the order of uniprimitive permutation groups. Ann. Math. 113(3), 553–568 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bailey R.F.: The metric dimension of small distance-regular and strongly regular graphs. Australas. J. Combin. 62(1), 18–34 (2015)

    MathSciNet  MATH  Google Scholar 

  6. Bailey R.F., Cáceres J., Garijo D., González A., Márquez A., Meagher K., Puertas M.L.: Resolving sets for Johnson and Kneser graphs. European J. Combin. 34(4), 736–751 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bailey R.F., Cameron P.J.: Base size, metric dimension and other invariants of groups and graphs. Bull. London Math. Soc. 43(2), 209–242 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bailey R.F., Meagher K.: On the metric dimension of Grassmann graphs. Discrete Math. Theor. Comput. Sci. 13(4), 97–104 (2011)

    MathSciNet  MATH  Google Scholar 

  9. Ball S., Blokhuis A.: On the size of a double blocking set in PG(2, q). Finite Fields Appl. 2(2), 125–137 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  10. Beardon A.F.: Resolving the hypercube. Discrete Appl. Math. 161(13-14), 1882–1887 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  11. Blumenthal L.M.: Theory and Applications of Distance Geometry. Clarendon Press, Oxford (1953)

    MATH  Google Scholar 

  12. Brouwer A.E., Cohen A.M., Neumaier A.: Distance-Regular Graphs. Springer-Verlag, Berlin (1989)

    Book  MATH  Google Scholar 

  13. Brouwer A.E., Haemers W.H.: Spectra of Graphs. Springer-Verlag, New York (2012)

    Book  MATH  Google Scholar 

  14. Cáceres J., Hernando C., Mora M., Pelayo I.M., Puertas M.L., Seara C., Wood D.R.: On the metric dimension of Cartesian products of graphs. SIAM J. Discrete Math. 21(2), 423–441 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Cameron, P.J.: Biplanes. Math. Z. 131(1), 85–101 (1973)

  16. van Dam, E.R., Koolen, J.H., Tanaka, H.: Distance-regular graphs. Electron. J. Combin. #DS22 (2016)

  17. Feng M., Wang K.: On the metric dimension of bilinear forms graphs. Discrete Math. 312(6), 1266–1268 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  18. Fijavž, G., Mohar B.: Rigidity and separation indices of Paley graphs. Discrete Math. 289(1-3), 157–161 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  19. Gardiner A.: Antipodal covering graphs. J. Combin. Theory Ser. B 16(3), 255–273 (1974)

    Article  MathSciNet  MATH  Google Scholar 

  20. Godsil C.D., Hensel A.D.: Distance regular covers of the complete graph. J. Combin. Theory Ser. B 56(2), 205–238 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  21. Graham, R.L., Knuth, D.E., Patashnik, O.: Concrete Mathematics: a Foundation for Computer Science. Addison–Wesley, Reading, Mass. (1989)

  22. Gravier, S., Parreau, A., Rottey, S., Storme, L., Vandomme, É.: Identifying codes in vertex-transitive graphs and strongly regular graphs. Electron. J. Combin. 22(4), #P4.6 (2015)

  23. Guo, J., Li, F., Wang, K.: Incidence matrices of finite attenuated spaces and class dimension of association schemes. Discrete Math. 315–316, 42–46 (2014)

  24. Guo J., Li F., Wang K.: Resolving sets for four families of distance-regular graphs. Adv. Geom. 14(1), 129–134 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  25. Guo J., Wang K., Li F.: Metric dimension of symplectic dual polar graphs and symmetric bilinear forms graphs. Discrete Math. 313(2), 186–188 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  26. Guo J., Wang K., Wang K., Wang K.: Metric dimension of some distance-regular graphs. J. Combin. Optim. 26(1), 190–197 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  27. Haemers W.H., Xiang Q.: Strongly regular graphs with parameters (\({4m^{4}, 2m^{4} +m^{2}, m^{4}+m^{2}, m^{4}+m^{2}}\)) exist for all \({m > 1}\). European J. Combin. 31(6), 1553–1559 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  28. Harary F., Melter R.A.: On the metric dimension of a graph. Ars Combin. 2, 191–195 (1976)

    MathSciNet  MATH  Google Scholar 

  29. Héger, T., Takáts, M.: Resolving sets and semi-resolving sets in finite projective planes. Electron. J. Combin. 19(4), #P30 (2012)

  30. Ionin Y.J., Shrikhande M.S.: Combinatorics of Symmetric Designs. Cambridge University Press, Cambridge (2006)

    Book  MATH  Google Scholar 

  31. Knuth D.E.: Big Omicron and big Omega and big Theta. ACM SIGACT News 8(2), 18–24 (1976)

    Article  Google Scholar 

  32. McKay B.D., Spence E.: Classification of regular two-graphs on 36 and 38 vertices. Australas. J. Combin. 24, 293–300 (2001)

    MathSciNet  MATH  Google Scholar 

  33. Rudvalis A.: (\({v, k, \lambda}\))-graphs and polarities of (\({v, k, \lambda}\))-designs. Math. Z. 120(3), 224–230 (1971)

    Article  MathSciNet  MATH  Google Scholar 

  34. Sebő A., Tannier E.: On metric generators of graphs. Math. Oper. Res. 29(2), 383–393 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  35. Seidel, J.J., Taylor, D.E.: Two-graphs: a second survey. In: Lovász, L., Sós, V.T. (Eds.) Algebraic Methods in Graph Theory (Szeged, 1978), Colloq. Math. Soc. János Bolyai (2nd ed.) 25, pp. 689–711. North-Holland, Amsterdam/New York (1981)

  36. Slater P.J.: Leaves of trees. Congr. Numer. 14, 549–568 (1975)

    MathSciNet  MATH  Google Scholar 

  37. Smith D.H.: Primitive and imprimitive graphs. Quart. J. Math. Oxford Ser. (2) 22(4), 551–557 (1971)

    Article  MathSciNet  MATH  Google Scholar 

  38. Spence, E.: Is Taylor’s graph geometric? Discrete Math. 106–107, 449–454 (1992)

  39. Spence, E.: Two-graphs. In: Colbourn, C.J., Dinitz, J.H. (eds.) Handbook of Combinatorial Designs, pp. 875–882. CRC Press, Boca Raton (2007)

  40. Taylor D.E.: Regular two-graphs. Proc. London Math. Soc. (3) 35(2), 257–274 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  41. Taylor D.E.: Two-graphs and doubly transitive groups. J. Combin. Theory Ser. A 61(1), 113–122 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  42. Taylor, D.E., Levingston, R.: Distance-regular graphs. In: Holton, D.A., Seberry, J. (eds.) Combinatorial Mathematics (Proc. Internat. Conf. Combinatorial Theory, Australian Nat. Univ., Canberra, 1977), Lecture Notes in Math., Vol. 686, pp. 313–323. Springer-Verlag, Berlin (1978)

Download references

Author information

Authors and Affiliations

  1. School of Science and Environment (Mathematics), Grenfell Campus, Memorial University of Newfoundland, University Drive, Corner Brook, NL, A2H 6P9, Canada

    Robert F. Bailey

Authors
  1. Robert F. Bailey
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Robert F. Bailey.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bailey, R.F. On the Metric Dimension of Imprimitive Distance-Regular Graphs. Ann. Comb. 20, 641–659 (2016). https://doi.org/10.1007/s00026-016-0334-9

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00026-016-0334-9

Mathematics Subject Classification

Keywords

Search

Navigation