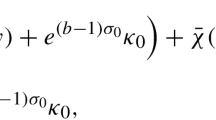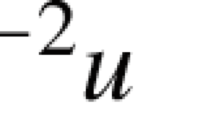Abstract
In this article we deal with gradient h-almost Yamabe solitons introduced by Zeng (J Math Study 54(4):371–386 2021). In this setting we prove that under some conditions in the potential function, Ricci curvature or parabolicity of M, then the scalar curvature is a constant. Also proved that under some integral conditions, a gradient h-Yamabe soliton most be scalar curvature vanished.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Barbosa, E., Ribeiro, E., Jr.: On conformal solutions of the Yamabe flow. Arch. Math. 101, 79–89 (2013)
Caminha, A., Sousa, P., Camargo, F.: Complete foliations of space forms by hypersurfaces. Bull. Braz. Math. Soc. 41(3), 339–353 (2010)
Cao, H.D., Sun, X., Zhang, Y.: On the structure of gradient Yamabe solitons. Math. Res. Lett. 19, 767–774 (2012)
Cheeger, J., Colding, T.H.: Lower bounds on Ricci curvature and the almost rigidity of warped products. Ann. Math. 144(1), 189–237 (1996)
Colding, T.H., Minicozzi, W.P.: A Course in Minimal Surface, vol. 121. Amer. Math. Soc. (2011)
Cunha, A.W.: Remarks on scalar curvature of gradient Yamabe solitons with non-positive Ricci curvature. Differ. Geom. Appl. 80, 101843 (2022)
Cunha, A.W., Shaikh, A.A., Mandal, P.: Some characterizations of gradient Yamabe solitons. J. Geom. Phys. 167, 104293 (2021)
Grigor’yan, A.: Analytic and geometric background of recurrence and non-explosion of the Brownian motion on Riemannian manifolds. Bull. Am. Math. Soc. 36(2), 135–249 (1999)
Hamilton, R.S.: Lectures on Geometric Flows (1989). (Unpublished)
Hamilton, R.S.: The Ricci flow on surfaces, Mathematics and general relativity. Contemp. Math. 71, 237–262 (1988)
Huang, G., Li, H.: On a classification of the quasi Yamabe gradient solitons. Methods Appl. Anal. 21, 379–390 (2014)
Leandro, B., Pina, H.: Generalized quasi Yamabe gradient solitons. Differ. Geom. Appl. 49, 167–175 (2016)
Ma, L., Miquel, V.: Remarks on scalar curvature of Yamabe solitons. Ann. Glob. Anal. Geom. 42, 195–205 (2012). https://doi.org/10.1007/s10455-011-9308-7
Pigola, S., Rigoli, M., Rimoldi, M., Setti, A.: Ricci almost solitons. Ann Sc. Norm. Super. Pisa Cl. Sci. Ser. (5) 10, 757–799 (2011)
Schoen, R., Yau, S.T.: Lectures on Differential Geometry, Conference Proceedings and Lecture Notes in Geometry and Topology. I. International Press, Cambridge (1994)
Troyanov, M.: Solving the p-Laplacian on manifolds. Proc. Am. Math. Soc. 128(2), 541–545 (1999)
Yau, S.T.: Some function-theoretic properties of complete Riemannian manifolds and their applications to geometry. Indiana Univ. Math. J. 25, 659–670 (1976)
Zeng, F.: On the h-almost Yamabe Soliton. J. Math. Study 54(4), 371–386 (2021)
Acknowledgements
The authors would like to thank Prosenjit Mandal for comments and valuable conversations. Also the authors would like to thank the referee for his/her comments which improve this work and the mananding Editor for comments. The first author is partially supported by CNPq, Brazil, Grant 430998/2018-0 and FAPEPI (Edital 007-2018).
Funding
Funding was provided by CNPq (Grant Number 430998/2018-0), FAPEPI (Grant Number PPP-Edital 007/ 2018).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there was no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Cunha, A.W., Siddiqi, M.D. Characterizations of Gradient h-Almost Yamabe Solitons. Results Math 78, 47 (2023). https://doi.org/10.1007/s00025-022-01821-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00025-022-01821-2