Skip to main content
SpringerLink
Log in

A Characterization of the Disc by the Angle of the Support Cone

  • Published:
Results in Mathematics Aims and scope Submit manuscript

Abstract

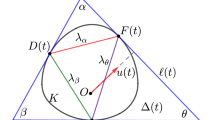
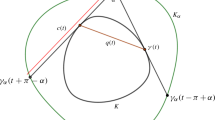
Let K be a body in the plane and let \(\lambda <1\) be a positive real number. Suppose that for every \(x\in \mathbb R^2\) such that \(\lambda K + x\) is exteriorly tangent to K, the common support cone of K and \(\lambda K + x\) has a constant angle \(\alpha \). Suppose that one of the following conditions is satisfied: (a) K is a body of constant width, (b) K is centrally symmetric. Then K is a Euclidean disc.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Chinn, W.G., Steenrod, N.E.: First Concepts of Topology. The Geometry of Mappings of Segments, Curves, Circles, and Disks, New Mathematical Library, vol. 18. Random House, New York (1966)

    Book  Google Scholar 

  2. Cieślak, W., Miernowski, A., Mozgawa, W.: Isoptics of a closed strictly convex curve. Lect. Notes Math. 1481, 28–35 (1991)

    Article  MathSciNet  Google Scholar 

  3. Cieślak, W., Miernowski, A., Mozgawa, W.: Isoptics of a closed strictly convex curve II. Rend. Sem. Mat. Univ. Padova 96, 37–49 (1996)

    MathSciNet  MATH  Google Scholar 

  4. García-Jiménez, M., González, E., Jerónimo-Castro, J.: A characterization of the Euclidean sphere with respect to an isoptic surface. Monatsh. Math. 181, 601–607 (2016)

    Article  MathSciNet  Google Scholar 

  5. Groemer, H.: Geometric Applications of Fourier Series and Spherical Harmonics. Cambridge University Press, Cambridge (1996)

    Book  Google Scholar 

  6. Gutkin, E.: Capillary floating and the billiard ball problem. J. Math. Fluid Mech. 14, 363–382 (2012)

    Article  MathSciNet  Google Scholar 

  7. Hammer, P.C.: Convex curves of constant Minkowski breadth. Proc. Sympos. Pure Math. VII, 291–304 (1963)

    Article  MathSciNet  Google Scholar 

  8. Jerónimo-Castro, J., Rojas-Tapia, M.A., Velasco-García, U., Yee-Romero, C.: An isoperimetric type inequality for isoptic curves of convex bodies. Results Math. 75, 1–12 (2020)

    Article  Google Scholar 

  9. Valentine, F.A.: Convex Sets. McGraw-Hill Series in Higher Mathematics, McGraw-Hill, New York (1964)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Facultad de Ingeniería, Universidad Autónoma de Querétaro, Cerro de las Campanas s/n, C.P. 76010, Querétaro, Mexico

    Jesús Jerónimo-Castro

Authors
  1. Jesús Jerónimo-Castro
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jesús Jerónimo-Castro.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jerónimo-Castro, J. A Characterization of the Disc by the Angle of the Support Cone. Results Math 76, 130 (2021). https://doi.org/10.1007/s00025-021-01446-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00025-021-01446-x

Keywords

Mathematics Subject Classification

Search

Navigation