On the Relative Distances of Nine Points in the Boundary of a Plane Convex Body

Abstract

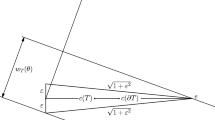
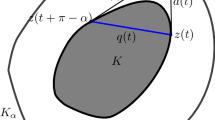
Let C be a plane convex body. The relative distance (or C-distance) of points $a, b\in C$ is defined by the ratio of the Euclidean distance of a and b to the half of the Euclidean distance of $a_{1}, b_{1}\in C$, where $a_{1}b_{1}$ is a longest chord of C parallel to the line-segment ab. Denote by $\phi _{k}(C)$ the greatest possible number d such that the boundary of C contains k points in pairwise C-distance at least d and denote by ${\mathcal {C}}$ the family of plane convex bodies. Let $\phi _{k}({\mathcal {C}})=\sup \{\phi _{k}(C)\mid C\in {\mathcal {C}}\}$. In this paper we prove $\phi _{9}({\mathcal {C}})=\sqrt{3}-1$.