Abstract
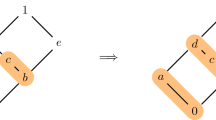
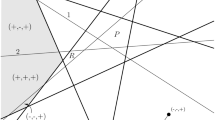
Varchenko introduced a distance function on chambers of hyperplane arrangements that he called quantum bilinear form. That gave rise to a determinant indexed by chambers whose entry in position (C, D) is the distance between C and D: that is the Varchenko determinant. He showed that that determinant has a nice factorization. Later, Aguiar and Mahajan defined a generalization of the quantum bilinear form, and computed the Varchenko determinant given rise by that generalization for central hyperplane arrangements and their cones. This article takes inspiration from their proof strategy to compute the Varchenko determinant given rise by their distance function for apartment of hyperplane arrangements. Those latter are in fact realizable conditional oriented matroids.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Aguiar, M., Mahajan, S.: Topics in Hyperplane Arrangements, vol. 226. Mathematical Surveys and Monographs, Providence (2017)
Bandelt, H.-J., Chepoi, V., Knauer, K.: COMs: complexes of oriented matroids. J. Combin. Theory Ser. A 156, 195–237 (2018)
Denham, G., Hanlon, P.: Some Algebraic Properties of the Schechtman-Varchenko Bilinear Forms, vol. 38. New Perspectives in Geometric Combinatorics, MSRI Publications, Berkeley (1999)
Gao, Y., Zhang, Y.: Diagonal form of the Varchenko matrices. J. Algebraic Combin. 48, 351–368 (2018)
Gente, R.: The Varchenko Matrix for Cones. Ph.D. Thesis, Philipps-Universität Marburg (2013)
Hanlon, P., Stanley, R.: A \(q\)-deformation of a trivial symmetric group action. Trans. Am. Math. Soc. 350(11), 4445–4459 (1998)
Hochstättler, W., Welker, V.: The Varchenko determinant for oriented matroids. Math. Z. 293(3–4), 1415–1430 (2019)
Margolis, S., Saliola, F., Steinberg, B.: Cell complexes, poset topology and the representation theory of algebras arising in algebraic combinatorics and discrete geometry. Mem. Am. Math. Soc. (to appear)
Olzhabayev, A., Zhang, Y.: Diagonal Form of the Varchenko Matrices for Oriented Matroids. arXiv: 2001.06460
Pfeiffer, G., Randriamaro, H.: The Varchenko determinant of a Coxeter arrangement. J. Group Theory 21(4), 651–665 (2018)
Randriamaro, H.: A deformed quon algebra. Commun. Math. 27, 103–112 (2019)
Randriamaro, H.: A multiparametric quon algebra. Bull. Iran. Math. Soc. (to appear). https://doi.org/10.1007/s41980-020-00414-5
Randriamaro, H.: Computing the Varchenko Determinant of Collages, and Application in Infinite Statistics. arXiv: 1910.01675
Schechtman, V., Varchenko, A.: Quantum Groups and Homology of Local Systems, Algebraic Geometry and Analytic Geometry. Springer, Berlin (1990)
Varchenko, A.: Bilinear form of real configuration of hyperplanes. Adv. Math. 97(1), 110–144 (1993)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was funded by my mother.
Rights and permissions
About this article
Cite this article
Randriamaro, H. The Varchenko Determinant for Apartments. Results Math 75, 86 (2020). https://doi.org/10.1007/s00025-020-01226-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00025-020-01226-z