Dynamic Stress Drop for Selected Seismic Events at Rudna Copper Mine, Poland

Abstract

In this paper, we report on an analysis of rupture processes of mining-induced events using the Empirical Green Function approach. The basic goal of this analysis is to estimate the dynamic stress drop—the quantity describing frictional forces at a slipping fault plane during the unstable part of an earthquake. The presented results cover 40 selected events with magnitude $M_{\rm{w}}$ ranging between 2.1 and 3.6 occurring in the Rudna copper mine (Poland) between 1996 and 2006. The spatial extent of the seismic network operated by the mine enabled us to estimate not only the dynamic stress drop but also the rupture velocities for most of the events studied. The results are analyzed in terms of correlations of the ratio of static to dynamic stress drop with other parameters characterizing the rupture processes. We also pose a question about the conditions of occurrence of over- and undershooting stress drop mechanisms. For all but two events, the estimated dynamic stress drop ranges between 0.1 and 4 MPa and is dominated by lower values. There are only two exceptions when it reaches the level of the order of 10 MPa. The reliability of these two exceptional cases is low, however. The rupture velocity, needed for dynamic stress drop calculation, was estimated from observed directivity effects. The obtained values ranged between 0.2 and almost 0.9 shear wave velocity, with dominating low velocities. The ratio of static to dynamic stress drop does not clearly correlate with the seismic scalar moment, source radius estimated according to Madariaga’s model, or static stress drop. It only positively correlates with the rupture velocity and ranges from values lower than 1 (undershooting mechanisms), mostly for slow events, up to values larger than 1 (overshooting mechanisms) for the majority of fast events. For all events with overshooting-type mechanisms, the estimated rupture velocity $V_{\rm{r}}$ was larger than half of the S-wave velocity $V_{\rm{s}}.$ On the other hand, for the undershooting-type events the associated rupture velocity was in most cases smaller than 0.6 $V_{\rm{s}}$ and large rupture speed was observed only in a few cases for this type of events.

1 Introduction

Seismic events, both natural earthquakes and those induced or triggered by human activity, like rockbursts in mines, are always related to stress change in the broadly understood source area. To describe the stress release effects, seismology uses three basic physical parameters, namely the static stress drop, the Coulomb stress transfer and the dynamic stress drop (Ben-Menahem and Singh 1981; Gibowicz and Kijko 1994; Udias et al. 2014).

These quantities provide estimates of the shear elastic stress release over a fault from the pre-event state to the post-event state (static stress drop), the spatial stress transfer from the fault to the neighborhood area (Coulomb stress transfer) and frictional stress during an unstable, sliding stage of the event (dynamic stress drop) (Kanamori and Rivera 2004; Gibowicz 2009). Among these three parameters the dynamic stress drop is the only one which brings direct information on the dynamics of the rupture process and together with the static stress drop provides some insight into the arresting mechanism of an earthquake. By comparing the dynamic and static stress drop one can distinguish between different types of rupture arresting mechanisms (Aki and Richards 1980; Gibowicz and Kijko 1994), as follows. During the sliding phase, the rupture can consume the whole available elastic strain energy and smoothly stop, which will lead to final stresses equal to the frictional stress. This situation is often referred to as an Orowan-type case (Udias et al. 2014). On the other hand, abrupt arresting of the rupture front, for example by fault heterogeneities, may lead to a rebuilding of the final stresses at a level higher than the frictional stress, leading to the undershooting case (previously called the partial stress drop). Finally, the inertia of the moving fault, physical processes like micro-branching of the rupture front and partial melting, to name a few (Kanamori and Brodsky 2004; Mulargia et al. 2004; Kanamori and Rivera 2006), can lead to a final stress lower than the frictional one, resulting in the overshooting mechanism. There are still many open questions connected with rupture arresting mechanisms, like whether there is any correlation of the arresting mechanism with other parameters describing the rupture process, what is a role of fault heterogeneities in rupture arresting (Candela et al. 2011; Senatorski 2014), what is the thermodynamics of the arresting mechanisms, to name a few. To answer such questions, knowledge of the dynamic stress drop is necessary.

The study of the dynamic stress drop for large earthquakes has attracted a lot of attention for years (see, e.g., Zuniga 1993; Mori et al. 2003; Abercrombie and Rice 2005). The situation is more complex when small earthquakes are concerned (Mori et al. 2003) because propagation effects contribute more strongly to observed seismograms in a frequency pass-band important for analysis (Abercrombie 2015). Particularly good conditions for dynamic stress drop analysis are provided by anthropogenic seismicity, especially seismicity induced by deep mining (Gibowicz 2009). For this type of seismicity there exist favorable conditions for analyzing the dynamics of seismic ruptures because seismic networks usually operate underground at extraction levels providing a very high signal-to-noise ratio even at high frequencies with feeble noise and extensive spatial azimuth coverage. Moreover, since deep mines usually operate in shallow sedimentary layers, the geology of the medium is often relatively simple. This is the case, for example, with the Rudna copper mine (Lizurek et al. 2015). Surprisingly, in spite of these favorable conditions, an analysis of the dynamic stress drop for mining-induced events has never been reported yet. Only recently, Gibowicz (2009) addressed this task and considered the dynamic stress drop for mining rockbursts, but many issues are still waiting for a deeper analysis, especially an analysis of the reliability of the solutions obtained. In this paper, we continue the previous efforts of Domanski et al. (2001, 2002a, b), Debski and Domanski (2002), Domanski and Gibowicz (2003, 2008), and Gibowicz (2009), and report our first results of dynamic stress drop analysis for selected seismic events from the Rudna copper mine.

In the analysis presented here, we took advantage of the relatively large seismic activity in the Rudna mine which allows the Empirical Green Function approach to be used efficiently (Hartzell 1978; Domanski and Gibowicz 2008). The dense seismic networks run together by the Rudna and Polkowice mines consist of 64 seismometers operating mostly at the extraction level (Domanski and Gibowicz 2008) with distance to the hypocentre ranging from tens of meters up to about 10 km. This enables not only the calculation of standard source parameters and verification of scaling relations (Domanski and Gibowicz 2008; Gibowicz 2009) at the $M\sim$ 1–3 scale, but also the calculation of dynamic parameters: the rupture velocity and the sought dynamic stress drop. Analyzing the spatial variability of the source time functions we were able to infer the rupture velocity in a model-independent way (Ben-Menahem and Singh 1981; Udias et al. 2014), and analyzing the properties of the source time function we can estimate the dynamic stress drop (Boatwright 1980).

The approach presented in this paper goes beyond the classical analysis of microseismic events. However, many analyses of anthropogenic seismicity have been discussing similar issues, like for example scaling relations, overshooting/undershooting conditions, source complexity, etc. (see, e.g., Urbancic and Trifu 1996; Gibowicz 1997, 1998; Ogasawara et al. 2002; Imanishi and Ellsworth 2006; Kwiatek et al. 2011). The good review of such analysis is a collection of three papers by Gibowicz (1990, 2009) and Gibowicz and Lasocki (2001).

The paper is structured as follows. To fix the notation we begin by recalling the notions of partial stress drop and dynamic stress drop. Then, the Empirical Green Function technique used for calculating the source time function is briefly described and the mining data and the data processing method are described in detail. The paper ends with a discussion of the results.

2 Static and Dynamic Stress Drops

Rock bursts in mines are accompanied by a sudden and abrupt fall of the stresses in the rocks resulting from an unstable slip of rock masses along a given fault plane. These stress changes are important for rock mass stability and possible acceleration (or suppression) of the subsequent seismic activity in the surrounding area (King and Coco 2000; Orlecka-Sikora 2010). Two widely used physical parameters describing the stress changes due to an earthquake rupture, namely the static stress drop and the dynamic stress drop, can be obtained from seismic records. Let us briefly describe them after Gibowicz and Kijko (1994), Udias et al. (2014) and Mori et al. (2003).

The static stress drop is defined as the difference of the shear stresses existing prior to a rupture ($\sigma _0$) and after it ($\sigma _1$)

$$\begin{aligned} \Delta \sigma _{\rm{s}}= \sigma _0- \sigma _1 \end{aligned}$$

(1)

averaged over the rupture plane. It is connected to the seismic scalar moment and the source size which for circular source model (the most often used in mining data analysis) is given by the well-known relation (see, e.g., Udias et al. 2014), originally put forward by Eshelby (1957)

$$\begin{aligned} \Delta \sigma _{\rm{s}}= \frac{7}{16} \frac{M_{\rm{o}}}{R^3}, \end{aligned}$$

(2)

where $M_{\rm{o}}$ is the seismic scalar moment and R is the source size. While $M_{\rm{o}}$ can be directly estimated from seismic records, estimating the source radius requires either using a rupture model (Aki and Richards 1980), analysis of aftershock distribution if available (Gibowicz and Kijko 1994), inversion of coseismic displacements (Jiang et al. 2013), or performing source tomography imaging (see, e.g., Bouchon et al. 2002). In the first case, which is adopted in this paper, the most often used source models have been proposed by Brune (1970) and Madariaga (1976). Actually, in mining seismology the model of Madariaga (1976) is preferable because it provides smaller, more realistic estimates of the source radius (Gibowicz and Kijko 1994; Gibowicz 2004).

The second well-known parameter describing the stress changes during an earthquake rupture is the dynamic stress drop ($\Delta \sigma _{\rm{d}}$). It is defined as the difference between the initial stresses $\sigma _0$ in the source area and frictional stresses ($\sigma _{\rm{f}}$) acting on the rupture plane during the sliding phase of an earthquake

$$\begin{aligned} \Delta \sigma _{\rm{d}}= \sigma _0- \sigma _{\rm{f}} \end{aligned}$$

(3)

averaged over the rupture plane and rupture duration (Mori et al. 2003). The dynamic stress drop can be estimated from the source time function (STF) S(t) retrieved from far-field recordings using the method developed by Boatwright (1980) and used, for example, by Mori et al. (2003) and Abercrombie and Rice (2005) to study small earthquakes. Knowing S(t) and assuming constant rupture velocity, the dynamic stress drop can be expressed as (Boatwright 1980; Mori et al. 2003)

$$\begin{aligned} \Delta \sigma _{\rm{d}}= \frac{M_{\rm{o}} }{4 \pi V_{\rm{r}}^3}( 1 - \xi ^2)^2\frac{\delta S}{\bar{S}}, \end{aligned}$$

(4)

where $( 1 - \xi ^2)^2$ is a geometric factor (assumed to be equal to 0.75), $V_{\rm{r}}$ is the rupture velocity, and $\delta S$ and $\bar{S}$ are the initial slope and area of STF, respectively. Applying this relation to each considered recording station and averaging out the results, one can obtain the required estimate of the average dynamic stress drop.

To analyze the relations between $\Delta \sigma _{\rm{d}}$ and other source parameters we follow the approach of Zuniga (1993) and use the $\epsilon$ parameter defined as

$$\begin{aligned} \epsilon = \frac{\Delta \sigma _{\rm{s}}}{\Delta \sigma _{\rm{d}}}. \end{aligned}$$

(5)

With this definition, $\epsilon = 1$ corresponds to the Orowan-type models when the final stress equals the frictional stress, $\epsilon > 1$ corresponds to the overshooting mechanism and $\epsilon < 1$ describes the undershooting mechanism.

An advantage of working with the $\epsilon$ parameter rather than directly with $\Delta \sigma _{\rm{s}}$ and $\Delta \sigma _{\rm{d}}$ is that this parameter should in principle be less sensitive to data processing errors than the static and dynamic stress drops separately. The point is that estimation of $\Delta \sigma _{\rm{s}}$ and $\Delta \sigma _{\rm{d}}$ requires knowledge of source size (in our analysis R) and rupture velocity $V_{\rm{r}},$ respectively. Estimation of these quantities from seismic records is prone to data processing technical details. Moreover, they are fundamentally dependent (in a weak sense) since, under the constant rupture velocity assumption R is proportional to the product of $V_{\rm{r}}$ and rupture duration (Domanski and Gibowicz 2008). Assuming constant rupture velocity we thus can get rid of R and $V_{\rm{r}}$ parameters from $\epsilon$ since they appear in the same (cubic) power in $\Delta \sigma _{\rm{s}}$ and $\Delta \sigma _{\rm{d}}$ so

$$\begin{aligned} \epsilon = \frac{7 \pi }{4 ( 1 - \xi ^2)^2} \frac{1}{T^3}\frac{\bar{S}}{\delta S}. \end{aligned}$$

(6)

It follows from this formula that $\epsilon$ explicitly depends only on the basic characteristics of STF: its integral ($\bar{S}$), initial slope-rise time ($\delta S$), width (T), and is thus fully determined by data only.

From the point of view of stress changes in the source area, the seismic rupture process can be divided into three intervals (Udias et al. 2014; Mulargia et al. 2004). The first, initiation period ends with an abrupt drop of the shearing stress on the rupture plane from the initial value $\sigma _0$ to the value $\sigma _{\rm{f}}$ determined by the frictional properties of the fault. In the second, sliding stage, the shearing stress on the fault remains approximately constant. Finally, when the rupture is arrested we can face three possibilities. The older hypothesis from Orowan (1960) assumes that during the arresting phase the elastic energy is smoothly absorbed and the final stress remains at the frictional level ($\sigma _1= \sigma _{\rm{f}}$). However, it is well known from observations (see, e.g., Gibowicz 2001) that an arresting mechanism can rebuild the stress over the rupture plane, leading to the undershooting process ($\sigma _1> \sigma _{\rm{f}}$). Finally, during the arresting phase, the shearing stress can fall below the frictional stress level ($\sigma _1< \sigma _{\rm{f}}$), in which case it is referred to as the overshooting mechanism. These three situations are schematically depicted in Fig. 1.

Fig. 1

A simplified sketch of the evolution of shearing stresses on a rupture plane during the three main phases of a rupture: weakening phase during which the traction drops to an average kinematic level, sliding phase represented by an idealized constant kinematic friction, and an arresting phase

3 STF Estimation: Empirical Green Function Technique

Estimating the dynamic stress drop requires knowledge of the source time function. One of the methods of its calculation from seismic records is the Empirical Green Function (EGF) technique. The approach has been proposed by Hartzell (1978) and implemented in practice by Mueller (1985) and by Domanski and Gibowicz (1999) for mining data. It relies on replacing an unknown Green’s function with a part of the waveform $u^{\rm{egf}}$ of another, much smaller seismic event (called Green’s event) that occurred in the closest neighborhood of the main event and had a similar focal mechanism. Following such substitution, the seismogram of the analyzed event recorded at the i-th station can be approximated by the following convolution

$$\begin{aligned} u^{\rm{obs}}_i(t) \approx \int \limits _{T} u^{\rm{egf}}_i(t-t') \tilde{S}_i(t') {\rm {d}}t', \end{aligned}$$

(7)

where $\tilde{S}(t)$ is the apparent source time function (ASTF) of the sought event with respect to the Green’s one $\tilde{S}(t) = S(t)/S^{\rm{egf}}(t).$ One can argue (Hartzell 1978; Mueller 1985; Domanski and Gibowicz 1999) that the approximation of STF by ASTF, namely $S_i(t) \approx \tilde{S}_i(t'),$ holds up the corner frequency of the Green’s event, provided its displacement spectrum is reasonably “flat”. We follow this assumption.

The essential point of the EGF technique is the careful choice of pairs of events (Abercrombie 2015). Based on our experience with an application of the EGF technique for Rudna-mine data we have set up the following basic empirical criteria which should be satisfied. The events should be located within a distance of 100–200 m, the differences between the P and T axes of the moment tensor solution should not exceed 20$^\circ$–30$^\circ ,$ and a difference $\Delta M =M^{\rm{main}} - M^{\rm{egf}}$ between magnitudes of main and Green’s events should be around 1 unit (Domanski and Gibowicz 1999; Domanski et al. 2002b). The last condition is to ensure a “flat” spectrum of the Green’s event in the frequency range of the larger event, which, for the Rudna mine usually occurs just for $\Delta M \approx 1$ (Domanski et al. 2002b). However, in case of events with a relatively “simple” STF functions (without a high-frequency radiation) we have observed that this condition is sometimes achieved at the $\Delta M$ as low as 0.5 unit.

Having selected $u^{\rm{egf}}(t),$ the inverse problem of retrieving the STF function becomes a deconvolution (inversion) task based on Eq. 7. This can be carried out either in the time domain or the frequency domain by appropriate inverse methods (see, e.g., Courboulex et al. 1996). However, the replacement of the “true” Green function with its EGF approximation can lead to non-physical solutions, for example, a negative STF (Domanski and Gibowicz 2001). This technical obstacle can be conveniently overcome by more advanced deconvolution methods like the Projected Landweber method (Bertero et al. 1997; Piana and Bertero 1997) (PLD) or the pseudo-spectral technique (Debski and Domanski 2002) which allow to introduce some physical constraints on the STF deconvolution. This is achieved, however, at the cost of changing the initial linear deconvolution into a nonlinear inverse process (Bertero et al. 1997; Debski and Domanski 2002) and the problem of non-uniqueness of the solution arises.

Having estimated STF for a number of stations providing extensive azimuthal coverage, one can try to estimate the rupture velocity (Domanski and Gibowicz 2003, 2008). For unilateral-type events the azimuthal variability of STF widths allows to estimate the rupture duration ($T_{\rm{o}}$), rupture length L,  and rupture velocity ($V_{\rm{r}}$) using the theoretical relation (Ben-Menahem and Singh 1981)

$$\begin{aligned} T_i = T_{\rm{o}} - \delta T \cos (\theta _i)\nonumber \\ T_{\rm{o}} = \frac{L}{V_{\rm{r}}}, \quad \delta T = \frac{L}{V_{\rm{p}}}, \end{aligned}$$

(8)

where $T_i$ is the width of the STF function recorded at the i-th station, $\theta _i$ is the angle between the direction to the i-th station and the rupture azimuth, and $V_{\rm{p}}$ is the P-wave velocity.

Evaluating the uncertainties of the obtained solutions is an important element of STF estimation. Unfortunately, this is an extremely complex problem. The main reason for this is that, actually, the EGF-based deconvolution is an infinite-dimensional inverse task (Debski 2010). We want to reconstruct the continuous function on the basis of two time-limited seismic records. Even if we consider a finite frequency band of the sought function, the inverse task still remains highly non-unique (Tarantola 2005). In practice, it means that the EGF technique is quite unstable and we have to introduce many, very subjective assumptions to stabilize the solution. Among other things, this includes the careful choice of a pair of events matching the location, moment tensor solution, shape of spectra and data filtering, to name a few, as closely as possible (Abercrombie 2015; Domanski and Gibowicz 2003). In case of multi-stations observations, the coherence of the solution among all stations has to be verified, and some stations may eventually be disregarded. All these elements have to be taken into account when EGF deconvolution results are quantitatively evaluated for inversion uncertainties.

Another important issue determining the quality of the final inversion is a choice of the length of EGF function. If taken too short, the obtained STF will be seriously biased. In consequence, the “synthetic seismogram” obtained by the convolution of the STF with the EGF can significantly differ from the seismogram of the main event. This situation is relatively easy to detect. However, too long EGF can lead to artificially complex STF.

An important element influencing uncertainties of the STF evaluation is an accuracy of the used inversion procedure. This point is well illustrated in Fig. 2, which shows how different inversion procedures influence inversion results. For these particular case, to obtain a good fit to the main event seismograms we had to use quite different EGF functions at different stations. In case of station 18, a simple (even slightly too short) EGF was sufficient to obtain a good fit and thus a reliable STF. However, the short EGF lead often to inversion (deconvolution) instabilities visible here as delta-like spikes in the STF solution when the Landweber projection method is used. On the other hand, for the station 4 a good fit to the main event seismogram was obtained only taking relatively long and complex EGF. Such a choice lead, however, to spurious secondary pick in the STF solutions whose existence and form strongly depended on the inversion method used. In practice, the possibility of quantitative uncertainty analysis of the EGF-based inversion is thus very limited.

Fig. 2

An example of uncertainties of retrieving the STF function due to a choice of EGF function and inversion procedures illustrated by two selected station records of the event of July 3, 1998 (No. 7 in Table 1) after Debski and Domanski (2002). All amplitudes are scaled separately (dimensionless ratios) for each subplot

Table 1 List of events used for the analysis of the dynamic stress drop

Table 2 Source parameters for the analyzed events

In spite of these principal limitations, some elements of the EGF inversion uncertainties can be estimated. For example, Domanski et al. (2001) and Domanski and Gibowicz (2003) have discussed the uncertainties of estimation of rupture duration and source size inferred from STF obtained by EGF deconvolution in the time and frequency domains. Debski and Domanski (2002) and Kwiatek (2008) have discussed the influence of particular parameterization of STF and the inversion technique on deconvolution results using Monte Carlo techniques. An interesting and practical method of estimating EGF-induced errors has been proposed by Prieto et al. (2006) if a sequence of aftershocks is available. The most advanced analysis of the error estimation task has recently been presented by Abercrombie (2015). In our analysis, we have not tried to perform a complete error analysis of the obtained results. Instead, whenever possible, we have used a simplified approach relying on a measuring observed discrepancies in solutions between different stations for a given event. Such estimator provides a lower bound limit of final errors (Debski 2010).

To summarize, the EGF method is very efficient for providing realistic source time function solutions but it does not allow to make a fully realistic error evaluation—“error bars” accompanying the EGF-based results should always be treated cautiously.

4 Data and Data Analysis Methodology

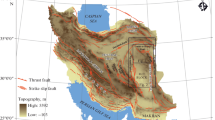
The dynamic stress drop analysis presented in this paper is based on seismic data from the Rudna and Polkowice–Sieroszowice copper mines. These mines, situated in south-western Poland (see, Fig. 3), run two digital seismic networks composed of 64 vertical seismometers, Wilmores MK-II and MK-III, located underground at depths ranging from 550 to 1150 m. The frequency band of the recording/transmission system is from 0.5 to 150 Hz and the sampling frequency is 500 Hz (sampling interval ${\rm{d}}t=2$ ms). Seismic signals from all sensors are transmitted in analogue form to the central unit where they are digitized with 14-bit resolution. The achieved dynamics is around 70 dB.

Fig. 3

Geographic location of the Rudna copper mine (open square)

The location of seismometers and epicentres of the analyzed seismic events is shown in Fig. 4.

Fig. 4

Left panel: joint seismic network of the Rudna and Polkowice–Sieroszowice copper mines (triangles) and epicentres (circles) of all analysed seismic events. Right panel: the epicenter (star) of the event of July 3, 1998 (No. 7 in Table 1) used as illustration of particular event solutions and stations (triangles) with their ID numbers contributing to the analysis of this event

Before selection of events for the dynamic stress drop analysis, the classical spectral analysis and moment tensor inversion were performed, as described in Gibowicz and Kijko (1994). The moment magnitudes of the events (listed in Table 1) were estimated during the MT inversion. However, as this inversion was performed in time domain (Wiejacz 1992), the obtained $M_{\rm{o}}$ (and magnitudes) can be quite uncertain. For this reason in the final analysis we have used $M_{\rm{o}}$ estimated from the spectral low-frequency levels of S waves as a more reliable estimator of seismic moment (Domanski and Gibowicz 2001, 2008; Gibowicz 2009). The values of parameters of the medium in the source area necessary for this calculation were the following: P- and S-wave velocity of 5700 and 3300 m/s, respectively, and average density $\rho = 2750$ ${\rm{{kg/m}}}^3.$ The analysis took into account corrections for the pass-band and signal-to-noise ratio limitation of the recording system (Ide and Beroza 2001). At this stage, Madariaga’s radius, static stress drop and scalar seismic moment were calculated, among others.

In the next step, the events were selected and paired for the STF deconvolution according to basic criteria described in the previous section. In addition, we have considered only the events for which non-DC component in the moment tensor solution was below 20%. The seismograms used were pre-filtered using a low pass Butterworth filter with cutting frequency of 30 Hz. At this stage, we ended up with about 60 pairs of events with magnitude ranging from $M = 2.1$ to $M=3.6$ (main events) and $M = 1.5$–2.4 for Green’s events. The pre-selected main-events were covering almost a full energy spectrum of events occurring in the Rudna mine (besides the smallest events). Selection of the Green’s events was always a trade-off between searching for a larger event which can provide high signal-to-noise ratio (SNR) and better azimuth coverage and smaller one fulfilling the criterion of one magnitude unit differences. For the smallest events the criterion of large SNR (availability of data from larger number of stations) was actually more important than a strict obeying of the magnitude difference rule. The price for this was, however, a need for a more careful selection of the main and corresponding EGF events. In consequence of such procedure, the Green’s events for the largest main events were relatively larger than for the smaller main events. We have accepted such situation because it gives an additional cross-check of correctness of the analysis. Concluding the magnitude differences between the main and Green’s events were ranging from 0.6 unit for smaller events up to almost 1.5 for the largest main events, as shown in Fig. 5.

Fig. 5

Magnitudes of Green’s events $M^{\rm{{egf}}}$ (left panel) and the difference $\Delta M =M^{\rm{{main}}} - M^{\rm{{egf}}}$ between magnitudes of main and Green’s events (right panel) as a function of $M^{\rm{{main}}}.$ For majority of the considered events $\Delta M$ is larger than 0.8 magnitude unit. Only for the smallest events we have accepted, (for strictly selected pairs) the differences of 0.6 magnitude unit. Circles denote circular-type events while squares stand for unilateral ones

The distances between the hypocentres of main and Green’s events were no larger than 250 m in the case of the largest events and around 20–50 m for the smallest ones. The differences between the P and T axes of the moment tensor solutions were below $30{^\circ }.$

Next, the STF inversion was carried out using the projected Landweber and (in some cases) Bayesian Monte Carlo-based pseudo-spectral method. The details of the STF calculation technique with some elementary uncertainty analysis can be found in (Domanski et al. 2002b; Domanski and Gibowicz 2003; Debski and Domanski 2002; Debski 2008). For each event the STF solutions were verified for their “regularity” and consistency among all available stations. If the solutions for a few stations (typically 1–3) were significantly different from others, the “noisy” stations were skipped, provided the remaining ones still gave good azimuthal coverage. Otherwise, an event was dismissed from further analysis. At this stage, we also verified if the integrals of STF calculated for each station were consistent among themselves.

The solutions which passed the above selection were next inspected for an azimuthal dependence of the STF width and classified as circular- or unilateral-type events as follows. First, we have calculated Pearson’s correlation coefficient $R_{\rm{c}}$ measuring to what extent the pulse width and cosine of station-rupture azimuth are linearly correlated. Events for which $|R_{\rm{c}}| >0.6$ were classified as unilateral and the remaining ones as circular. The particular choice of the above threshold value of $R_{\rm{c}}$ is rather arbitrary and is essentially based on inspection of all considered at this stage events. The obtained values of $R_{\rm{c}}$ for considered events are listed in Table 2.

For the circular-type events the rupture velocity was a priori assumed to be $V_{\rm{r}} = 1/2\,V_{\rm{S}},$ which is the average rupture velocity reported in the previous studies (Domanski et al. 2002b; Domanski and Gibowicz 2008). This particular value, smaller than typically reported rupture velocity for natural earthquakes (usually in the 0.7–0.9 $V_{\rm{S}}$ range) follows from an observation that at the Rudna mine the rupture velocities are relatively small, usually in the 0.3–0.7 $V_{\rm{S}}$ range (Domanski and Gibowicz 2008). A similar range of $V_{\rm{r}}$ has been also reported by Imanishi et al. (2004) for similar in range micro-earthquake in Japan.

For the unilateral events the rupture duration ($T_{\rm{o}}$), rupture velocity, rupture length and azimuth were estimated by the linear LSQR fit of pulse widths against azimuth using Eq. 8 and the associated errors were estimated. For the circular events $T_{\rm{o}}$ was calculated as the average over all available stations and corresponding root mean square differences were taken as the error estimators.

Next, for each event the dynamic stress drops were calculated for each station according to Eq. 4, inspected to see whether they exhibited “regular behaviour”, averaged out, and are reported as $\Delta \sigma _{\rm{d}}$ in Table 2. In principle, $\Delta \sigma _{\rm{d}}$ should be azimuth-independent and have the same value for all stations. However, due to many simplifications this is not a case and some variability between individual stations was observed. This discrepancy is quantified by the RMS deviation from the average value and is denoted by $\delta _{\Delta \sigma _{\rm{d}}}$ in Table 2. We assume it to be the main source of errors contributing to $\Delta \sigma _{\rm{d}}$ uncertainties. Events for which $\Delta \sigma _{\rm{d}}$ was different than $2 \delta _{\Delta \sigma _{\rm{d}}}$ even for a single station were rejected.

Finally, 40 events passed the applied selection criteria and were accepted for further analysis. At this stage the $\epsilon$ parameter was independently calculated according to Eq. 6. All results are finally listed in Table 2.

To illustrate the results of the described analysis chain, few selected ASTF functions obtained for the event No. 7. by the advanced Bayesian Monte-Carlo based approach (Debski 2008) are shown in Fig. 6. Figure 7 shows the azimuthal distribution of the STF widths and STF rise times for the same event. In this figure, we indicated the Id numbers of stations (see Fig. 4) for which given values were obtained and the plotted error bars were estimated within the Bayesian inversion schemata (see Debski 2008, 2010 for details).

Fig. 6

Selected ASTF functions retrieved for a few stations of the event of July 3, 1998 (event No. 7 in Table 1) by the pseudo-spectral method (Debski 2008)

Fig. 7

 The example of ASTF solution parameters for the event of July 3, 1998 (No. 7 in Table 1). Left panel: variation of the source width with the difference between the station’s azimuth and the rupture propagation direction. The best linear fit according to Eq. 8 is shown. Right panel: the similar dependence of the pulse rise time ($\delta S$). Stations contributing to estimating STF of these event are shown in right panel of Fig. 4. Error bars were estimated by the Monte Carlo inverse method (see Debski 2008 for details)

Additionally, in Fig. 8 we plot the source radius estimated according to the Madariaga’s model. For the purpose of the current analysis we used this particular estimator of the rupture size to be consistent with a similar analysis of Mori et al. (2003), Abercrombie and Rice (2005) and our previous analysis (Domanski and Gibowicz 2008). Moreover, this model provides more reasonable solution for mining events, as it has been pointed out by Gibowicz and Kijko (1994).

Fig. 8

Source radius calculated according to Madariaga’s model for the analyzed events

Finally, in Fig. 9 the STF “bar” widths ($T_{\rm{o}}$) are plotted against $M_{\rm{o}}$ for all analyzed events.

Fig. 9

Source width $T_{\rm{o}}$ as a function of $M_0$ for the considered events. Events with over- and undershooting mechanisms are represented by triangles and circles respectively

5 Results

The main results of our analysis are gathered in Table 2 where static and dynamic stress drops (averaged over all stations available for a given event), rupture duration, rupture velocity, and corresponding error estimators are listed. The following set of figures illustrates the basic features and the relations between these parameters.

The rupture velocity for unilateral-type events is plotted in Fig. 10 against $M_{\rm{o}}.$ Although this figure suggests a weak positive correlation between $V_{\rm{r}}$ and $M_{\rm{o}},$ the small value of the corresponding Pearson’s coefficient $R_{\rm{c}} = 0.3$ suggests that any possible correlation is statistically unimportant. However, it is clearly visible that for all overshooting-type events the rupture velocity is relatively high ($V_{\rm{r}} >0.5\, V_{\rm{s}}$). On the other hand, most undershooting events are characterized by smaller rupture velocities $V_{\rm{r}} <0.6\, V_{\rm{s}}.$

Fig. 10

Rupture velocity against seismic moment $M_{\rm{o}}.$ Circles denote undershooting events while triangles represent overshooting cases. Only unilateral events are plotted for which $V_{\rm{r}}$ could be calculated from azimuthal variations of the STF widths. The plotted errors are standard LSQR-fit errors

In Fig. 11 the calculated dynamic stress drops, as well as static stress drops are plotted for all events against scalar seismic moment $M_{\rm{o}}.$ As follows from this figure, the dynamic and static stress drops are quite similar for lower $M_{\rm{o}}$ but for larger $M_{\rm{o}},$ the dynamic stress drop seems to become systematically larger than $\Delta \sigma _{\rm{s}}$. We also observe a slight increase of $\Delta \sigma _{\rm{d}}$ and $\Delta \sigma _{\rm{s}}$ with increasing $M_{\rm{o}},$ but again it is a statistically unimportant correlation.

Fig. 11

Static stress drop $\Delta \sigma _{\rm{s}}$ (triangles) and dynamic stress drop $\Delta \sigma _{\rm{d}}$ (circles—undershooting events, stars—overshooting events) for the analyzed events. The obtained values are in good agreement with the solutions of Abercrombie and Rice (2005) for natural events of a similar magnitude range. Error bars comprise only a variation of $\Delta \sigma _{\rm{d}}$ among the available stations

In Fig. 12 the dynamic stress drop is plotted against the rupture velocity. The plotted errors are variances of $\Delta \sigma _{\rm{d}}$ solutions due to differences between stations contributing to given event. All but two solutions are consistently lower then approximately 5 MPa. Large errors (relatively large inconsistency between $\Delta \sigma _{\rm{d}}$ calculated from different stations suggest that obtained solutions for two outliers are quite uncertain. No correlation between $\Delta \sigma _{\rm{d}}$ and $V_{\rm{r}}/V_{\rm{s}}$ is visible.

Fig. 12

Dynamic stress drop $\Delta \sigma _{\rm{d}}$ (circles—undershooting events, stars—overshooting events) as a function of the rupture velocity. The estimated $\Delta \sigma _{\rm{d}}$ is independent of $V_{\rm{r}}/V_{\rm{s}}.$ Large errors for two events with the largest $\Delta \sigma _{\rm{d}}$ does not allow a reliable interpretation of these two exceptional solutions

The dependence of static to dynamic stress drop $\epsilon$ against $M_{\rm{o}}$ is shown in Fig. 13. Two important conclusions follow from this figure. First, we have observed both overshooting and undershooting events. The latter dominate in our dataset but this could be the effect of the particular event selection procedure. Second, no significant dependence of $\epsilon$ on $M_{\rm{o}}$ is visible, neither for unilateral-type nor for circular-type events. We have also noticed that in a statistical sense $\epsilon$ is independent of the size (R) of events (Fig. 14) and of the static stress drop $\Delta \sigma _{\rm{s}}$, (Fig. 15). Pearson’s correlation coefficient for the ${\rm{log}}(\epsilon )$ and other source parameters reads

$$\begin{aligned}&R^{\log (M_{\rm{o}}),\log (\epsilon )} = 0.0\nonumber \\&R^{R,\log (\epsilon )} = -\,0.1\nonumber \\&R^{\Delta \sigma _{\rm{s}},\log (\epsilon )} = 0.2\nonumber \\&R^{V_{\rm{r}}/V_{\rm{s}},\log (\epsilon )} = 0.64\nonumber \\ \end{aligned}$$

(9)

which clearly indicates that $\epsilon$ correlates only with the rupture velocity. For this particular case, shown in Fig. 16, we have estimated the best fit assuming the linear relation $\log (\epsilon ) = a + b \;(V_{\rm{r}}/V_{\rm{s}})$ using the full Bayesian inversion technique and taking into account the variation of uncertainties of $\epsilon$ due to $\delta _{\Delta \sigma _{\rm{d}}}$ errors. The maximum likelihood solution found is $a^{\rm{ml}} = -\,2.7 \pm 0.2$ and $b^{\rm{ml}} = 4.2 \pm 0.4.$

Fig. 13

Ratio of static to dynamic stress drop against seismic moment $M_{\rm{o}}.$ Circles denote circular-type events while squares mark unilateral ones

Fig. 14

Ratio of static to dynamic stress drop against the Madariaga rupture radius. Circles denote circular-type events while squares mark unilateral ones

Fig. 15

Ratio of static to dynamic stress drop against the static stress drop. Circles denote circular-type events while squares mark unilateral ones

Fig. 16

Ratio of static to dynamic stress drop against the rupture velocity. A trend of increasing $\epsilon$ with rupture velocity is visible. The Pearson correlation coefficient reads $R_{\rm{c}} = 0.64,$ justifying using a linear fit: $\log (\epsilon ) = a + b \;(V_{\rm{r}}/V_{\rm{s}}).$ The minimum least squares fit obtained for $a = -\,2.7, \; b = 4.2$ is shown by a dashed line. Only the unilateral events are plotted

Although more advanced uncertainty analysis is beyond the scope of this paper, a simple evaluation of uncertainty of the dynamic stress drop calculations based on dispersion of $\Delta \sigma _{\rm{d}}$ among different stations has been performed and is shown in Fig. 17. It is interesting to note, that the errors are systematically smaller for overshooting type events than for undershooting ones. Moreover, they are practically independent of the strength of events and $V_{\rm{r}}.$ In other words, the overshooting type events were visible as more consistent station-to-station solutions than the remaining ones. Keeping in mind that overshooting mechanism is visible mostly for faster rupturing events (see Fig. 16) it suggest that higher rupturing speed can mask some “smaller scale” processes which are responsible for a larger variability of STF solutions at different observational angles.

Fig. 17

Dynamic stress drop errors—a contribution from dispersions of $\Delta \sigma _{\rm{d}}$ among different stations as a function of $M_{\rm{o}}$ (left) and $V_{\rm{r}}$ (right)

6 Discussion and Conclusions

This and previous (Domanski and Gibowicz 2008) papers summarize our experience of using the EGF technique for studying the source parameters of seismic events induced by mining at the Rudna copper mine. Undertaking the task of dynamic stress drop calculation was possible due to the existence of a spatially dense seismic network at the Rudna and Polkowice–Sieroszowice copper mines. We have explored this opportunity to calculate the dynamic stress drop and the rupture velocity for 40 selected seismic events. We have found the analyzed dataset to include both overshooting (11 events) and undershooting mechanisms (29 events). We do not know if the more frequent occurrence of undershooting events has a physical background or results from our selection procedure.

To assure the highest possible reliability of the analysis, we have very carefully selected available seismic events. The resulting dataset represents solutions consistent with previous analysis (Domanski and Gibowicz 2008) with respect to such parameters like rupture velocity, rupture duration, source radius, and static stress drop. As far as the dynamic stress drop is considered, for all but two cases we obtained consistent values below $\Delta \sigma _{\rm{d}}< 4.5$ MPa with an average $\Delta \sigma_{\rm{d}}\approx 1$ MPa. For two exceptional events (events No. 22 and 38 with magnitudes $M=3.3$ and $M=3.5$) calculated $\Delta \sigma _{\rm{d}}$ were significantly larger: $13 \pm 7$ and $8.1 \pm 5$ MPa. Moreover, the estimated errors—a dispersion of $\Delta \sigma _{\rm{d}}$ among different stations—were also the largest in the whole data set. We are not sure if the observed large dynamic stress drops for these two events are really physical. Large discrepancies between different stations for these events suggest a low reliability of these two solutions.

Within the analyzed dataset, we have observed that for the undershooting events the static and dynamic stress drops have similar values for small $M_{\rm{o}},$ but for $M_{\rm{o}} > 10^{13}$ Nm dynamic stress drops are systematically larger than static stress drops (see Fig. 11). For events with overshooting mechanisms, the dynamic and static stress drops have comparable values with differences of less than 0.6 MPa independently of $M_{\rm{o}}.$

As far as the rupture velocity is concerned, the current results are in good agreement with our previous analysis (see Domanski and Gibowicz 2008, for details), indicating that for most seismic events at the Rudna mine the rupture velocities are relatively low. Similar results has been reported by Imanishi et al. (2004).

While the static-to-dynamic stress drop ratio seems to be independent of source parameters describing the size and strength of an event, like the scalar seismic moment, source radius or static stress drop, it positively correlates with rupture velocity. This positive correlation means that the overshooting mechanism tends to be preferred by “fast” ruptures while the undershooting one occurs mostly for slower ones. Moreover, it seems that in the analyzed dataset there exists a threshold rupture velocity $V_{\rm{rt}}\approx 0.5\, V_{\rm{s}}$ below which the overshooting does not occur. The increasing probability of occurrence of the overshooting mechanisms with rupture velocity is not surprising and can be explained by an inertia effect (Kanamori and Rivera 2006). On the other hand, the existence of a threshold rupture velocity below which this type of mechanism is not observed is more intriguing. Let us discuss this point in more depth.

The observation that the overshooting mechanisms occur only for fast events ($V_{\rm{r}} > V_{\rm{rt}}$) suggests that in the case of speedy ruptures the elastic strain energy release rate is large enough to (sometimes) trigger inertia-type effects or additional energy dissipation processes. A good candidate for such additional process is the multiple micro-fracturing of rocks near a fault plane (see, e.g., Patinet et al. 2014). Such processes can significantly reduce the strength of the fault and surrounding rocks and lead to a decrease in the effective frictional coefficient during the arresting phase. Overshooting can then be expected. However, for high-speed rupture processes, we have also observed a number of undershooting mechanisms. This suggests that physical mechanisms leading to overshooting are not always activated. Thus, there have to be additional factors controlling the arresting mechanisms in the high-speed rupture regime. At this point, the question arises about the role of thermodynamic processes (diffusive heat transfer, heat waves, etc.) in the case of the two considered (slow and fast) classes of events (see, e.g., Kanamori and Rivera 2006). The fault plane roughness can also be a factor contributing in a different way to the fast and slow arresting mode (Candela et al. 2011). The scenario described above is one of a number of possible explanations of the observed effect.

Actually, it is hard to offer any conclusive statements on the basis of the presented data because of the insufficient representation of overshooting cases and the relatively small number of analyzed events. Also, the limitations of the presented analysis are quite severe. For technical reasons, we have to deal with quantities averaged over the whole seismic source, which efficiently reduces the whole analysis to a point-like source model. Even taking into account that in the case of the analyzed events the linear dimensions of the source area are relatively small, reducing them to point-like sources introduces uncertainties that are difficult to estimate. On the other hand, a more advanced analysis based on waveform inversion still encounters many difficulties (Lizurek et al. 2015). Nowadays, one serious obstacle is the necessity of efficient simulation of waveforms in a frequency band up to about 20–30 Hz. Inversion of such high-frequency seismograms is still a challenging task. However, recent developments in finite difference simulations on unstructured grids (Waskiewicz and Dębski 2014) as well as time reversal inversion techniques (Larmat et al. 2006; Kawakatsu and Montagner 2008; Waskiewicz and Dębski 2018) make such an analysis quite plausible in near future. Using the waveform inversion will allow to overcome most limitations of the EGF approach. Nevertheless, the EGF approach is currently the only technique practically usable for analyzing the dynamics of mining-induced seismic events (Gibowicz 2009).