On Self-Gravitating Polytropic Elastic Balls

Abstract

A new four-parameters family of constitutive functions for spherically symmetric elastic bodies is introduced which extends the two-parameters class of polytropic fluid models widely used in several applications of fluid mechanics. The four parameters in the polytropic elastic model are the polytropic exponent $\gamma$, the bulk modulus $\kappa$, the shear exponent $\beta$ and the Poisson ratio $\nu \in (-1,1/2]$. The two-parameters class of polytropic fluid models arises as a special case when $\nu =1/2$ and $\beta =\gamma$. In contrast to the standard Lagrangian approach to elasticity theory, the polytropic elastic model in this paper is formulated directly in physical space, i.e., in terms of Eulerian state variables, which is particularly useful for the applications, e.g., to astrophysics where the reference state of the bodies of interest (stars, planets, etc.) is not observable. After discussing some general properties of the polytropic elastic model, the steady states and the homologous motion of Newtonian self-gravitating polytropic elastic balls are investigated. It is shown numerically that static balls exist when the parameters $\gamma ,\beta$ are contained in a particular region ${\mathcal {O}}$ of the plane, depending on $\nu$, and proved analytically for $(\gamma ,\beta )\in {\mathcal {V}}$, where ${\mathcal {V}}\subset {\mathcal {O}}$ is a disconnected set which also depends on the Poisson ratio $\nu$. Homologous solutions describing continuously collapsing balls are constructed numerically when $\gamma =4/3$. The radius of these solutions shrinks to zero in finite time, causing the formation of a center singularity with infinite density and pressure. Expanding self-gravitating homologous elastic balls are also constructed analytically for some special values of the shear parameter $\beta$.

Appendix: Proof of Theorem 1

Recall that a solution of (4.2) in the interval [0, R) is called regular if $\delta \in C^0([0,R))\cap C^1((0,R))$ and $\delta (r)>0$, for all $r\in [0,R)$, and strongly regular if in addition $\delta \in C^1([0,R))$ and $\lim _{r\rightarrow 0^+}\delta (r)=0$; see Sect. 2.6. The following lemma contains results on the limit $r\rightarrow R_{{\mathrm {max}}}^-$ of regular solutions defined up to the maximal radius $R_{{\mathrm {max}}}$.

Lemma 5

Let $\gamma \in {\mathbb {R}}$, $\beta \ne 0$ and $\delta _c>0$. Assume that there exists a unique regular solution of (4.2) satisfying $\eta (0)=\delta (0)=\delta _c>0$ and defined in a maximal radius interval $[0,R_{{\mathrm {max}}})$, $R_{{\mathrm {max}}}>0$. Then, the following holds:

• (i) If $R_{{\mathrm {max}}}<\infty$, then $\lim _{r\rightarrow R_{{\mathrm {max}}}^-}\delta (r)=0$ and $\lim _{r\rightarrow R_{{\mathrm {max}}}^-}\eta (r)>0$;

• (ii) If $R_{{\mathrm {max}}}=\infty$, then $\lim _{r\rightarrow \infty }\delta (r)=\lim _{r\rightarrow \infty }\eta (r)=0$.

Proof

The inequalities $\delta (r)<\eta (r)$ and $\eta '(r)<0$, for $r\in (0,R_{{\mathrm {max}}})$, will be used in the following arguments, see Lemma 4.

• (i) We begin by showing that $\delta (r)$ has a (finite) limit when $r\rightarrow R_{{\mathrm {max}}}^-$. This is obvious when $\beta \le \gamma$, as in this case $\delta (r)$ is non-increasing. Let $\beta >\gamma$. For $\beta \le 2$, we write the $\delta$-equation in (4.2) as

  $$\begin{aligned} \delta '=\frac{3(\beta -\gamma )}{r}{\widetilde{B}}(\delta /\eta )\eta -\theta r \eta ^{1+\beta -\gamma }\delta ^{2-\beta }, \end{aligned}$$

  (A.1)

  where ${\widetilde{B}}(y)=B(y)y^{1-\beta }$ is bounded for $y\in [0,1]$. Hence for $r\in (0,R_{{\mathrm {max}}})$, there holds

  $$\begin{aligned} |\delta '(r)|\le \frac{c_1}{r}+c_2 r, \end{aligned}$$

  where $c_1,c_2$ are positive constants. It follows that $|\delta '|$ is bounded in the interval $(0,R_{{\mathrm {max}}})$ and thus $\delta (r)$ converges as $r\rightarrow R_{{\mathrm {max}}}^-$ when $\beta \le 2$. For $\beta >2$, we instead write the $\delta$-equation as

  $$\begin{aligned} \frac{1}{\beta }(\delta ^{\beta })'=\delta ^{\beta -1} \delta '=\frac{3(\beta -\gamma )}{r}B(\delta /\eta )\eta ^{\beta }-\theta r\eta ^{1+\beta -\gamma }\delta \end{aligned}$$

  and since B(y) is bounded on [0, 1] for $\beta >2$, we obtain as before that $|(\delta ^{\beta })'|$ is bounded on $(0,R_{{\mathrm {max}}})$. Hence, $\delta ^{\beta }(r)$ converges as $r\rightarrow R_{{\mathrm {max}}}^-$, and so $\lim _{r\rightarrow R_{{\mathrm {max}}}^-}\delta (r)$ exists for all $\beta \ne 0$. It will now be proved that this limit is zero. Assume, by contradiction, that $\lim _{r\rightarrow R_{{\mathrm {max}}}^-}\delta (r)>0$. Then, there exists $c\in (0,1)$ such that $c<\delta (r)/\eta (r)<1$, for all $r\in (0,R_{{\mathrm {max}}}$), which implies that the right hand side of (4.2) is bounded on $(0,R_{{\mathrm {max}}})$. But then $|\delta '|$ is bounded on $(0,R_{{\mathrm {max}}})$, contradicting the hypothesis that $R_{{\mathrm {max}}}<\infty$. Hence, $\lim _{r\rightarrow R_{{\mathrm {max}}}^-}\delta (r)=0$ and

  $$\begin{aligned} \lim _{r\rightarrow R_{{\mathrm {max}}}^-}\eta (r)=\frac{3}{R_{{\mathrm {max}} }^3}\int _0^{R_{{\mathrm {max}}}}\delta (s) s^2\,\mathrm{d}s>0, \end{aligned}$$

  must hold when $R_{{\mathrm {max}}}<\infty$.

• (ii) Let $\eta _\infty =\lim _{r\rightarrow \infty }\eta (r)$. If $\eta _\infty =0$, then $\lim _{r\rightarrow \infty }\delta (r)=0$ and thus the claim follows. Assume $\eta _\infty >0$; in particular $\eta _\infty<\eta (r)<\eta (0)=\delta _c$, for all $r\in (0,\infty )$. As in (i) we start by showing that $\lim _{r\rightarrow \infty }\delta (r)$ exists, which again is obvious for $\beta \le \gamma$. Let $\beta >\gamma$ and assume first $\beta \ge 1$. In this case, we rewrite the $\delta$-equation in (4.2) as

  $$\begin{aligned} \delta '= & {} \left( \frac{\delta }{\eta }\right) ^{1-\beta }\eta ^{2-\gamma }\delta \left( \frac{3(\beta -\gamma )}{r}\frac{B(\delta /\eta )}{\delta /\eta }\eta ^{\gamma -2} -\theta r\right) \\\le & {} \left( \frac{\delta }{\eta }\right) ^{1-\beta }\eta ^{2-\gamma }\delta (c r^{-1}-\theta r), \end{aligned}$$

  where c is a positive constant and where we used that B(y)/y is bounded for $y\in (0,1)$ and $\beta \ge 1$. Hence, $\delta '(r)<0$ for $r>\sqrt{c/\theta }$ and thus $\lim _{r\rightarrow \infty }\delta (r)$ exists when $\beta \ge 1$. Assume now $\beta <1$. Then by (A.1), we can write

  $$\begin{aligned} \delta '(r)= & {} \frac{3(\beta -\gamma )}{r}\frac{{\widetilde{B}}(\delta /\eta )}{\delta /\eta }\delta -\theta r\eta ^{1+\beta -\gamma }\delta ^{2-\beta }\\\le & {} \frac{c_1}{r}\delta -c_2 r\delta ^{2-\beta }, \end{aligned}$$

  where $c_1,c_2$ are positive constants and where we used that ${\widetilde{B}}(y)/y=B(y)y^{-\beta }$ is bounded for $\beta <1$. Hence $\delta (r)\le u(r)$ for $r\ge 1$, where

  $$\begin{aligned}&u(r)=\left( \frac{c_2(1-\beta )}{2+c_1(1-\beta )}r^2+\frac{\delta (1)^{\beta -1}(2+c_1(1-\beta ))-c_2(1-\beta )}{2+c_1(1-\beta )}\frac{1}{r^{c_1(1-\beta )} }\right) ^{-1/(1-\beta )} \end{aligned}$$

  is the solution of $u'(r)=c_1u(r)/r-c_2r u(r)^{2-\beta }$ with $u(1)=\delta (1)$. We conclude that $\delta (r)\rightarrow 0$ as $r\rightarrow \infty$ when $\beta <1$. We claim that $\delta (r)$ converges to zero at infinity even when $\beta >1$. Assume $\lim _{r\rightarrow \infty }\delta (r)=\delta _\infty >0$; then

  $$\begin{aligned}&\delta '(r)\sim \left( \frac{\delta _\infty }{\eta _\infty }\right) ^{1-\beta } \left( \frac{3(\beta -\gamma )}{r}B(\delta _\infty /\eta _\infty )\eta _\infty -\theta r\eta _\infty ^{2-\gamma }\delta _\infty \right) \rightarrow -\infty ,\\&\quad \quad \text { as }r\rightarrow \infty , \end{aligned}$$

  a contradiction. Hence, $\lim _{r\rightarrow \infty }\delta (r)=0$ must hold and thus also $\lim _{r\rightarrow \infty }\eta (r)=0$, by L’Hôpital’s rule.

$\square$

In the next proposition, the existence of strongly regular solutions to (4.2) in a maximal radius interval $[0,R_{{\mathrm {max}}})$ is proved and sufficient conditions on the parameters $\gamma ,\beta$ are given such that $R_{{\mathrm {max}}}$ is finite or $R_{{\mathrm {max}}}=\infty$.

Proposition 4

For all $\gamma \in {\mathbb {R}}$, $\beta \ne 0$ and $\delta _c>0$, the system (4.2) admits a unique strongly regular local solution $(\delta ,\eta )$ such that $\delta (0)=\eta (0)=\delta _c$. Letting $[0,R_{{\mathrm {max}}})$ be the maximal radius interval of definition of this solution the following holds:

${{\mathrm {(A)}}}$:

If $\gamma >2$ and $1<\beta \le \gamma$, then $R_{{\mathrm {max}}}<\infty$;

${{\mathrm {(B)}}}$:

If $0<\gamma \le \beta <1$ or $\beta <\gamma \le 1$, then $R_{{\mathrm {max}}}=\infty$ and $\lim _{r\rightarrow \infty }y(r)=\frac{4-3\gamma }{3(2-\gamma )}$.

Proof

Assume first $\gamma \ne 2$. The change of variables

$$\begin{aligned} y=\delta /\eta ,\quad v=\theta r^2\eta ^{2-\gamma }y^{1-\beta },\quad \xi =\log r \end{aligned}$$

transforms (4.2) into the autonomous dynamical system

$$\begin{aligned} \frac{dy}{d\xi }&=[\Upsilon (y)-v]y,\end{aligned}$$

(A.2a)

$$\begin{aligned} \frac{dv}{d\xi }&=[(1-\beta )(\Upsilon (y)-v)+2-3(2-\gamma )(1-y)]v, \end{aligned}$$

(A.2b)

where

$$\begin{aligned} \Upsilon (y)=3(1-y)+3(\beta -\gamma )B(y)y^{-\beta }. \end{aligned}$$

(A.2c)

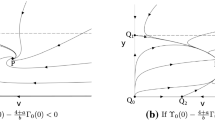
As $(dy/d\xi )_{y=1}<0$, for all $v>0$, the open region ${\mathcal {U}}=\{v>0, y<1\}$ of the state space is future invariant (which is equivalent to the bound $\eta >\delta$ proved in Lemma 4(ii)). A simple local stability analysis shows that the boundary point ${{\mathrm {O}}}$ with coordinates $v=0, y=1$ is an hyperbolic saddle. The positive eigenvalue of the linearized flow around ${{\mathrm {O}}}$ is equal to 2 and the corresponding eigenvector $-5\partial _y+\partial _v$ points toward the interior of ${\mathcal {U}}$. Hence, there exists exactly one orbit $\Gamma =(\Gamma _y,\Gamma _v)\subset {\mathcal {U}}$ such that $\lim _{\xi \rightarrow -\infty }\Gamma (\xi )={{\mathrm {O}}}$. Moreover, $1-y(\xi )\sim 5C e^{2\xi }$ and $v(\xi )\sim C e^{2\xi }$ as $\xi \rightarrow -\infty$ along this orbit, where C is a positive constant. This orbit corresponds to a one parameter family of regular solutions of (4.2) up to $\xi _*$ such that $\Gamma _y(\xi )>0$ for $\xi <\xi _*$, and by Lemma 4(i) these solutions are strongly regular. Uniqueness follows if we show that the constant C is uniquely determined by the center datum $\delta (0)=\eta (0)=\delta _c$. As $\gamma \ne 2$, this follows by the definition of v, which gives $C=\theta \delta _c^{2-\gamma }$. Assume now $\gamma =2$. In this case, the system (4.2) is equivalent to the following decoupled system on $y=\delta /\eta$ and $\eta$:

$$\begin{aligned} y'=\left( \frac{\Upsilon (y)}{r}-\theta r y^{1-\beta }\right) y,\quad \eta '=-\frac{3\eta }{r}(1-y). \end{aligned}$$

(A.3)

The same argument as above gives now a local unique regular solution of the y-equation with asymptotic behavior $y=1+O(r^2)$ as $r\rightarrow 0^+$, and thus uniqueness for the system (A.3) follows by simply integrating the $\eta$-equation with center datum $\eta (0)=\delta _c$. By Lemma 4, the unique regular solution is strongly regular, and thus, the first part of the proposition is proved.

Proof of (A): As $\beta \le \gamma$, we have

$$\begin{aligned} \delta '\le -\theta r \eta ^{1+\beta -\gamma }\delta ^{2-\beta }. \end{aligned}$$

(A.4)

For $\beta \le \gamma -1$, we use $\eta \le \eta (0)=\delta _c$ in (A.4) to obtain $\delta '\le -cr\delta ^{2-\beta }$, and thus

$$\begin{aligned} \delta (r)\le \left( \delta _c^{\beta -1}-\frac{c}{2}(\beta -1)r^2\right) ^{\frac{1}{\beta -1}}, \end{aligned}$$

which, as $\beta >1$, implies $R_{{\mathrm {max}}}<\infty$. For $\gamma -1<\beta \le \gamma$ we instead use $\eta >\delta$ in (A.4) to obtain $\delta '\le -\theta r\delta ^{3-\gamma }$, which, as $\gamma >2$, implies again $R_{{\mathrm {max}}}<\infty$.

Proof of (B): To prove ${{\mathrm {(B)}}}$, we study the qualitative behavior toward the future of the orbit $\Gamma$ of the dynamical system (A.2) originating from the fixed point ${{\mathrm {O}}}$. As $\beta <1$, the function $\Upsilon$ is bounded for $y\in [0,1]$ and

$$\begin{aligned} \Upsilon (0)=3\frac{1-\gamma }{1-\beta }\ge 0. \end{aligned}$$

In fact, a straightforward analysis shows that $\Upsilon (y)>0$ for all $y\in (0,1)$. In particular the region ${\mathcal {V}}=\{v>0, 0<y<1\}$ is future invariant and $\Gamma (\xi )\subset {\mathcal {V}}$, for all $\xi \in {\mathbb {R}}$. Moreover, $v'(\xi )\le (a-(1-\beta )v)v$, where $a=\sup _{y\in (0,1)}[(1-\beta )\Upsilon (y)+2-3(2-\gamma )(1-y)]<\infty$ and thus $v(\xi )\le a/(1-\beta )$ along the orbit $\Gamma$. It follows that the $\omega$-limit set $\omega (\Gamma )$ of $\Gamma$ is not empty. By Poincaré-Bendixson theorem, $\omega (\Gamma )$ must be one of the following sets: (1) a fixed point; (2) a periodic orbit; (3) a connected set consisting of a finite number of fixed points $\{P_1,\dots ,P_n\}$ together with homoclinic and heteroclinic orbits connecting $P_1,\dots ,P_n$. Let $\phi (y,v)=v^{-1}y^{\beta -2}$ and let F(v, y) denote the vector field in the right hand side of (A.2). Since $\nabla \cdot (\phi F)(y,v)=-3\phi (y,v)(1-\gamma (1-y))$ is negative for $\gamma \le 1$ and $(y,v)\in {\mathcal {V}}$, then, by Dulac–Bendixson theorem, no periodic orbits exist in the region ${\mathcal {V}}$ and thus the alternative (2) above is not possible. The alternative (3) can be ruled out by studying the stability properties of the fixed points of the flow. Besides ${{\mathrm {O}}}$, the dynamical system (A.2) admits the fixed points ${{\mathrm {Q}}}=(0,0)$ and

$$\begin{aligned} {{\mathrm {P}}}=(\Upsilon (y_{{\mathrm {P}}}),y_{{\mathrm {P}}}),\quad \text {where}\quad \ y_{{\mathrm {P}}}=\frac{4-3\gamma }{3(2-\gamma )}. \end{aligned}$$

No other fixed points are present when $\gamma \le 1$. A simple local stability analysis shows that ${{\mathrm {P}}}$ is an hyperbolic sink, and thus it is a local attractor for a one parameter family of interior orbits, while ${{\mathrm {Q}}}$ is an hyperbolic saddle. The stable manifold of ${{\mathrm {Q}}}$ is tangent to the axis $y=0$, while the unstable manifold is tangent to $v=0$. In particular, there is no interior orbit which converges to or emanates from ${{\mathrm {Q}}}$. Putting this information together, we conclude that none of the structures mentioned in the alternative (3) above exists in the region ${\mathcal {V}}$. Thus Poincaré Bendixson theorem entails that the fixed point ${{\mathrm {P}}}$ is the $\omega$-limit set of all orbits entering the region ${\mathcal {V}}$ and so in particular $\Gamma (\xi )\rightarrow {{\mathrm {P}}}$ as $\xi \rightarrow \infty$, which is equivalent to $\lim _{r\rightarrow \infty }y(r)=\frac{4-3\gamma }{3(2-\gamma )}$. $\square$

Proof of Theorem 1

When (4.4) holds, Proposition 4 gives that the maximal radius interval of definition of strongly regular solutions of (4.2) is finite and by Lemma 5(i)

$$\begin{aligned} y(r)=\frac{\delta (r)}{\eta (r)}\rightarrow 0,\quad \text {as }r\rightarrow R_{{\mathrm {max}}}^-. \end{aligned}$$

As $y(0)=1$ and $y_{{\mathrm {b}}}\in (0,1)$, there exists a unique $R\in (0,R_{{\mathrm {max}}})$ such that $y(r)>y_{{\mathrm {b}}}$ for $r\in [0,R)$ and $y(R)=y_{{\mathrm {b}}}$. Thus, letting $p_{{\mathrm {rad}}}(r)=F_{{\mathrm {rad}}}(\delta (r),\eta (r))$, we have $p_{{\mathrm {rad}}}(R)=0$ and $p_{{\mathrm {rad}}}(r)>0$, for $r\in [0,R)$. Moreover, by Lemma 4(iii),

$$\begin{aligned} p_{{\mathrm {tan}}}(r)=F_{{\mathrm {tan}}}(\delta (r),\eta (r))\ge p_{{\mathrm {rad}}}(r), \quad r>0. \end{aligned}$$

Hence, letting $\rho (r)={\mathcal {K}}\delta (r)$, we obtain that $(\rho ,p_{{\mathrm {rad}}},p_{{\mathrm {tan}}}){\mathbb {I}}_{r\le R}$ is a type ${{\mathrm {A}}}$ static self-gravitating elastic ball. When (4.5) holds, strongly regular solutions of (4.2) are global and $y\rightarrow \frac{4-3\gamma }{3(2-\gamma )}=y_\infty >0$ as $r\rightarrow \infty$, see again Proposition 4. Since the last inequality in (4.5) is equivalent to $y_\infty <y_{{\mathrm {b}}}$, then there exists $R\in (0,R_{{\mathrm {max}}})$ such that $y(r)>y_{{\mathrm {b}}}$ for $r\in [0,R)$ and $y(R)=y_{{\mathrm {b}}}$, and thus the proof can be completed as before. $\square$