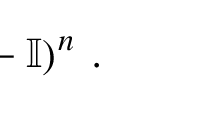Skip to main content
SpringerLink
Log in

On Wick Polynomials of Boson Fields in Locally Covariant Algebraic QFT

  • Published:
Annales Henri Poincaré Aims and scope Submit manuscript

Abstract

This work presents some results about Wick polynomials of a vector field renormalization in locally covariant algebraic quantum field theory in curved spacetime. General vector fields are pictured as sections of natural vector bundles over globally hyperbolic spacetimes and quantized through the known functorial machinery in terms of local \(*\)-algebras. These quantized fields may be defined on spacetimes with given classical background fields, also sections of natural vector bundles, in addition to the Lorentzian metric. The mass and the coupling constants are in particular viewed as background fields. Wick powers of the quantized vector field are axiomatically defined imposing in particular local covariance, scaling properties, and smooth dependence on smooth perturbation of the background fields. A general classification theorem is established for finite renormalization terms (or counterterms) arising when comparing different solutions satisfying the defining axioms of Wick powers. The result is specialized to the case of general tensor fields. In particular, the case of a vector Klein–Gordon field and the case of a scalar field renormalized together with its derivatives are discussed as examples. In each case, a more precise statement about the structure of the counterterms is proved. The finite renormalization terms turn out to be finite-order polynomials tensorially and locally constructed with the backgrounds fields and their covariant derivatives whose coefficients are locally smooth functions of polynomial scalar invariants constructed from the so-called marginal subset of the background fields. The notion of local smooth dependence on polynomial scalar invariants is made precise in the text. Our main technical tools are based on the Peetre–Slovák theorem characterizing differential operators and on the classification of smooth invariants on representations of reductive Lie groups.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Allen, B., Folacci, A.: Massless minimally coupled scalar field in de Sitter space. Phys. Rev. D 35, 3771–3778 (1987)

    Article  ADS  MathSciNet  Google Scholar 

  2. Anderson, I.M., Torre, C.G.: Two component spinors and natural coordinates for the prolonged Einstein equation manifolds. Tech. Rep., Utah State University (1994). Unpublished

  3. Anderson, I.M., Torre, C.G.: Classification of local generalized symmetries for the vacuum Einstein equations. Commun. Math. Phys. 176, 479–539 (1996). arXiv:gr-qc/9404030

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. Atiyah, M., Bott, R., Patodi, V.K.: On the heat equation and the index theorem. Invent. Math. 19, 279–330 (1973)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  5. Bär, C., Fredenhagen, K. (eds.): Quantum field theory on curved spacetimes: concepts and mathematical foundations. Lecture Notes in Physics, vol. 786. Springer (2009)

  6. Benini, M., Dappiaggi, C.: Models of free quantum field theories on curved background. In: Brunetti, R., Dappiaggi, C., Fredenhagen, K., Yngvason, J. (eds.) Advances in Algebraic Quantum Field Theory, Ch. 3. Springer, Berlin (2015)

    Google Scholar 

  7. Brouder, C., Dang, N .V., Laurent-Gengoux, C., Rejzner, K.: Properties of field functionals and characterization of local functionals. J. Math. Phys. 59, 023508 (2017). arXiv:1705.01937

    Article  ADS  MathSciNet  MATH  Google Scholar 

  8. Brunetti, R., Fredenhagen, K.: Microlocal analysis and interacting quantum field theories: renormalization on physical backgrounds. Commun. Math. Phys. 208, 623–661 (2000). arXiv:math-ph/9903028

    Article  ADS  MathSciNet  MATH  Google Scholar 

  9. Brunetti, R., Fredenhagen, K., Verch, R.: The generally covariant locality principle-a new paradigm for local quantum field theory. Commun. Math. Phys. 237, 31–68 (2003). arXiv:math-ph/0112041

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. Christoffel, E.B.: Über die Transformation der homogenen Differentialausdrücke zweiten Grades. J. Reine Angew. Math. 70, 46–70 (1869). http://eudml.org/doc/148073

  11. Dappiaggi, C., Drago, N.: Constructing Hadamard states via an extended Møller operator. Lett. Math. Phys. 106, 1587–1615 (2016). arXiv:1506.09122

    Article  ADS  MathSciNet  MATH  Google Scholar 

  12. Drago, N., Gérard, C.: On the adiabatic limit of Hadamard states. Lett. Math. Phys. 107, 1409–1438 (2017). arXiv:1609.03080

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. Drago, N., Hack, T.-P., Pinamonti, N.: The generalised principle of perturbative agreement and the thermal mass. Ann. Henri Poincaré 18, 807–868 (2017). arXiv:1502.02705

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. Fredenhagen, K., Rejzner, K.: Batalin-Vilkovisky formalism in the functional approach to classical field theory. Commun. Math. Phys. 314, 93–127 (2012). arXiv:1101.5112

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. Fulton, W.: Young Tableaux: With Applications to Representation Theory and Geometry. London Mathematical Society Student Texts, vol. 35. Cambridge University Press, Cambridge (1996)

    Book  Google Scholar 

  16. Gilkey, P.B.: Curvature and the eigenvalues of the Laplacian for elliptic complexes. Adv. Math. 10, 344–382 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  17. Goodman, R., Wallach, N.R.: Symmetry, Representations, and Invariants. Graduate Texts in Mathematics, vol. 255. Springer, New York (2009)

    Book  MATH  Google Scholar 

  18. Hack, T.-P., Pinamonti, N.: Cosmologial application of algebraic quantum field theory. In: Brunetti, R., Dappiaggi, C., Fredenhagen, K., Yngvason, J. (eds.) Advances in Algebraic Quantum Field Theory, Ch. 6. Springer, Berlin (2015)

    Google Scholar 

  19. Hollands, S.: Renormalized quantum Yang–Mills fields in curved spacetime. Rev. Math. Phys. 20, 1033–1172 (2008). arXiv:0705.3340

    Article  MathSciNet  MATH  Google Scholar 

  20. Hollands, S., Wald, R.M.: Local Wick polynomials and time ordered products of quantum fields in curved spacetime. Commun. Math. Phys. 223, 289–326 (2001). arXiv:gr-qc/0103074

    Article  ADS  MathSciNet  MATH  Google Scholar 

  21. Hollands, S., Wald, R.M.: Existence of local covariant time ordered products of quantum fields in curved spacetime. Commun. Math. Phys. 231, 309–345 (2002). arXiv:gr-qc/0111108

    Article  ADS  MathSciNet  MATH  Google Scholar 

  22. Hollands, S., Wald, R.M.: Conservation of the stress tensor in perturbative interacting quantum field theory in curved spacetimes. Rev. Math. Phys. 17, 227–311 (2005). arXiv:gr-qc/0404074

    Article  MathSciNet  MATH  Google Scholar 

  23. Jentsch, T.: The jet isomorphism theorem of pseudo-Riemannian geometry. arXiv:1509.08269

  24. Khavkine, I., Moretti, V.: Algebraic QFT in curved spacetime and quasifree Hadamard states: an introduction. In: Brunetti, R., Dappiaggi, C., Fredenhagen, K., Yngvason, J. (eds.) Advances in Algebraic Quantum Field Theory, Ch. 5. Springer, Berlin (2015)

    Google Scholar 

  25. Khavkine, I., Moretti, V.: Analytic dependence is an unnecessary requirement in renormalization of locally covariant QFT. Commun. Math. Phys. 344, 581–620 (2016). arXiv:1411.1302 [gr-qc]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. Kolař, I., Michor, P.W., Slovák, J.: Natural Operations in Differential Geometry. Springer, Berlin (1993)

    MATH  Google Scholar 

  27. Luna, D.: Fonctions différentiables invariantes sous l’opération d’un groupe réductif. Ann. Inst. Fourier 26, 33–49 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  28. Michor, P.W.: Topics in Differential Geometry. American Mathematical Society, Providence, RI (2008)

    MATH  Google Scholar 

  29. Parlett, B.N.: The (matrix) discriminant as a determinant. Linear Algebra Appl. 355, 85–101 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  30. Penrose, R.: A spinor approach to general relativity. Ann. Phys. 10, 171–201 (1960)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  31. Procesi, C.: Lie Groups: An Approach Through Invariants and Representations. Universitext. Springer, New York (2007)

    MATH  Google Scholar 

  32. Richardson, R.W.: Principal orbit types for real-analytic transformation groups. Am. J. Math. 95, 193–203 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  33. Richardson, R.W., Slodowy, P.J.: Minimum vectors for real reductive algebraic groups. J. Lond. Math. Soc. 42, 409–429 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  34. Rumberger, M.: Finitely differentiable invariants. Math. Z. 229, 675–694 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  35. Sahlmann, H., Verch, R.: Microlocal spectrum condition and Hadamard form for vector-valued quantum fields in curved spacetime. Rev. Math. Phys. 13, 1203–1246 (2001). arXiv:math-ph/0008029

    Article  MathSciNet  MATH  Google Scholar 

  36. Schambach, M., Sanders, K.: The Proca field in curved spacetimes and its zero mass limit. arXiv:1709.01911 [math-ph]

  37. Schouten, J.A.: Ricci-calculus: An Introduction to Tensor Analysis and Its Geometrical Applications. Grundlehren der mathematischen Wissenschaften, vol. 10, 2nd edn. Springer, Berlin (1954)

    Book  Google Scholar 

  38. Slovák, J.: Peetre theorem for nonlinear operators. Ann. Global Anal. Geom. 6, 273–283 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  39. Slovák, J.: On invariant operations on pseudo-Riemannian manifolds. Comment. Math. Univ. Carol. 33, 269–276 (1992). http://eudml.org/doc/247392

  40. Stephani, H., Kramer, D., MacCallum, M., Hoenselaers, C., Herlt, E.: Exact Solutions of Einstein’s Field Equations. Cambridge University Press, Cambridge (2003)

    Book  MATH  Google Scholar 

  41. Stoetzel, H.: Quotients of real reductive group actions related to orbit type strata. PhD thesis, Ruhr-Universitat Bochum (2008). http://nbn-resolving.de/urn/resolver.pl?urn=urn:nbn:de:hbz:294-23168

  42. Thomas, T.Y.: Differential Invariants of Generalized Spaces. CUP, Cambridge (1934)

    MATH  Google Scholar 

  43. Wald, R.M.: General Relativity. The University of Chicago Press, Chicago (1984)

    Book  MATH  Google Scholar 

  44. Zahn, J.: The renormalized locally covariant Dirac field. Rev. Math. Phys. 26, 1330012 (2014). arXiv:1210.4031

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to Charles Torre for sharing with them the unpublished report [2], also to Klaus Fredenhagen and Nicola Pinamonti for raising and clarifying some issues in Remark 13(6), and also to Jan Slovák for discussions that were helpful for “Appendix B.” IK was partially supported by the ERC Advanced Grant 669240 QUEST “Quantum Algebraic Structures and Models” at the University of Rome 2 (Tor Vergata). AM is grateful to the Math Dept. of University of Rome 2 (Tor Vergata) and of University of Milan for kind hospitality during the development of this work.

Author information

Authors and Affiliations

  1. Dipartimento di Matematica, Università di Milano and INFN Milano, Via Cesare Saldini, 50, 20133, Milan, MI, Italy

    Igor Khavkine

  2. Dipartimento di Fisica, Università di Trento and INFN-TIFPA Trento, Via Sommarive, 14, 38123, Povo, Trento, Italy

    Alberto Melati

  3. Dipartimento di Matematica, Università di Trento and INFN-TIFPA Trento, Via Sommarive, 14, 38123, Povo, Trento, Italy

    Valter Moretti

Authors
  1. Igor Khavkine
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alberto Melati
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Valter Moretti
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Valter Moretti.

Additional information

Communicated by Karl-Henning Rehren.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khavkine, I., Melati, A. & Moretti, V. On Wick Polynomials of Boson Fields in Locally Covariant Algebraic QFT. Ann. Henri Poincaré 20, 929–1002 (2019). https://doi.org/10.1007/s00023-018-0742-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00023-018-0742-y

Search

Navigation