Abstract
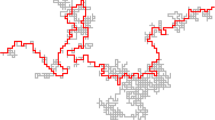
We study the probabilities with which chordal Schramm–Loewner evolutions (SLE) visit small neighborhoods of boundary points. We find formulas for general chordal SLE boundary visiting probability amplitudes, also known as SLE boundary zig-zags or order refined SLE multi-point Green’s functions on the boundary. Remarkably, an exact answer can be found to this important SLE question for an arbitrarily large number of marked points. The main technique employed is a spin chain–Coulomb gas correspondence between tensor product representations of a quantum group and functions given by Dotsenko–Fateev type integrals. We show how to express these integral formulas in terms of regularized real integrals, and we discuss their numerical evaluation. The results are universal in the sense that apart from an overall multiplicative constant the same formula gives the amplitude for many different formulations of the SLE boundary visit problem. The formula also applies to renormalized boundary visit probabilities for interfaces in critical lattice models of statistical mechanics: we compare the results with numerical simulations of percolation, loop-erased random walk, and Fortuin–Kasteleyn random cluster models at Q = 2 and Q = 3, and find good agreement.
Article PDF
Similar content being viewed by others
References
Alberts T., Kozdron M.J., Lawler G.F.: The Green’s function for the radial Schramm–Loewner evolution. J. Phys. A Math. Theor. 45, 494015 (2012)
Alberts T., Kozdron M.J.: Intersection probabilities for a chordal SLE path and a semicircle. Electron. Commun. Probab. 13, 448–460 (2008)
Alberts T., Sheffield S.: Hausdorff dimension of the SLE curve intersected with the real line. Electron. J. Probab. 13(40), 1166–1188 (2008)
Alberts, T., Sheffield, S.: The covariant measure of SLE on the boundary. Probab. Theory Relat. Fields 149(3), 331–371 (2011)
Bauer, M., Bernard, D.: SLE, CFT and zig-zag probabilities. In: Proceedings of the Conference ‘Conformal Invariance and Random Spatial Processes’, Edinburgh (2003)
Bauer M., Bernard D.: Conformal field theories of stochastic Loewner evolutions. Commun. Math. Phys. 239(3), 493–521 (2003)
Bauer M., Bernard D.: SLE martingales and the Virasoro algebra. Phys. Lett. B 557(3-4), 309–316 (2003)
Bauer M., Bernard D.: Conformal transformations and the SLE partition function martingale. Ann. Henri Poincaré 5(2), 289–326 (2004)
Beffara V., Duminil-Copin H.: The self-dual point of the two-dimensional random-cluster model is critical for \({q \geq 1}\). Probab. Theory Relat. Fields 153(3–4), 511–542 (2012)
Beffara V.: The dimension of the SLE curves. Ann. Probab. 36(4), 1421–1452 (2008)
Beliaev D., Izyurov K.: Proof of a factorization formula for critical percolation. Commun. Math. Phys. 310, 611–623 (2012)
Cardy J.L.: Critical percolation in finite geometries. J. Phys. A 25, L201–L206 (1992)
Chelkak D., Duminil-Copin H., Hongler C., Kemppainen A., Smirnov S.: Convergence of Ising interfaces to Schramm’s SLE curves. Comptes Rendus Math. de l’Acad. des Sci. 352(2), 157–161 (2014)
Camia F., Newman C.M.: Critical percolation exploration path and \({{\rm SLE}_6}\): a proof of convergence. Probab. Theory Relat. Fields 139(3-4), 473–519 (2007)
Chelkak D., Smirnov S.: Discrete complex analysis on isoradial graphs. Adv. Math. 228, 1590–1630 (2011)
Chelkak, D., Smirnov, S.: Universality in the 2D Ising model and conformal invariance of fermionic observables. Invent. Math. 189(3), 515–580 (2012). arXiv:0910.2045
Dotsenko V.S., Fateev V.A.: Conformal algebra and multipoint correlation functions in 2D statistical models. Nucl. Phys. B 240, 312 (1984)
Dubédat J.: SLE and Virasoro representations: localization. Commun. Math. Phys. 336(2), 695–760 (2015)
Dubédat J.: SLE and Virasoro representations: fusion. Commun. Math. Phys. 336(2), 761–809 (2015)
Edwards R.G., Sokal A.D.: Generalization of the Fortuin–Kasteleyn–Swendsen–Wang representation and Monte Carlo algorithm. Phys. Rev. D 38, 2009–2012 (1988)
Fortuin C.M., Kasteleyn P.W.: On the random-cluster model. I. Introduction and relation to other models. Physica 57, 536–564 (1972)
Flores S.M., Kleban P.: A solution space for a system of null-state partial differential equations. Part I. Commun. Math. Phys. 333(1), 389–434 (2015)
Flores S.M., Kleban P., Ziff R.M.: Cluster pinch-point densities in polygons. J. Phys. A Math. Theor. 45, 505002 (2012)
Felder G., Wieczerkowski C.: Topological representation of the quantum group Uq(sl2). Commun. Math. Phys. 138, 583–605 (1991)
Hagendorf, C.: A generalization of Schramm’s formula for SLE2. J. Stat. Mech. Theory Exp. P02033 (2009)
Hagendorf C., Le Doussal P.: SLE on doubly-connected domains and the winding of loop-erased random walks. J. Stat. Phys. 133, 231–254 (2008)
Hongler C., Kytölä K.: Ising interfaces and free boundary conditions. J. Am. Math. Soc. 26, 1107–1189 (2013)
Izyurov, K.: Critical Ising interfaces in multiply-connected domains (2013). arXiv:1309.5302
Kennedy T.: A fast algorithm for simulating the chordal Schramm–Loewner evolution. J. Stat. Phys. 128, 1125–1137 (2007)
Kytölä, K., Peltola, E.: Conformally covariant boundary correlation functions with a quantum group (2014). arXiv:1408.1384
Kytölä, K., Peltola, E.: Pure partition functions of multiple SLEs (2015). arXiv:1506.02476
Langlands, R.P., Pichet, C., Pouliot, P., Saint-Aubin, Y.: On the universality of crossing probabilities in two-dimensional percolation. J. Stat. Phys. 67(3–4), 553–574 (1992)
Lawler G.: Fractal and Multifractal Properties of SLE. Clay Mathematics Summer School, Buzios (2010)
Lawler, G.F.: Minkowski content of the intersection of a Schramm–Loewner evolution (SLE) curve with the real line. J. Math. Soc. Japan 67(4), 1631–1669 (2015). http://www.math.uchicago.edu/~lawler/minkreal.pdf. (Preprint)
Lawler G.F., Rezaei M.A.: Minkowski content and natural parameterization for the Schramm–Loewner evolution. Ann. Probab. 43(3), 1082–1120 (2015)
Lawler G.F., Sheffield S.: A natural parametrization for the Schramm–Loewner evolution. Ann. Probab. 39(5), 1896–1937 (2011)
Lawler G.F., Schramm O., Werner W.: Values of Brownian intersection exponents. I. Half-plane exponents. Acta Math. 187(2), 237–273 (2001)
Lawler G.F., Schramm O., Werner W.: Conformal invariance of planar loop-erased random walks and uniform spanning trees. Ann. Probab. 32(1B), 939–995 (2004)
Lawler G.F., Werness B.M.: Multi-point Green’s functions for SLE and an estimate of Beffara. Ann. Probab. 41(3A), 1513–1555 (2013)
Lawler G.F., Zhou W.: SLE curves and natural parametrization. Ann. Probab. 41(3A), 1556–1584 (2013)
Rohde S., Schramm O.: Basic properties of SLE. Ann. Math. (2) 161(2), 883–924 (2005)
Schramm O.: Scaling limits of loop-erased random walks and uniform spanning trees. Isr. J. Math. 118, 221–288 (2000)
Simmons J.J.H., Kleban P.: Complete conformal field theory solution of a chiral six-point correlation function. J. Phys. A Math. Theor. 44, 315403 (2011)
Simmons J.J.H., Kleban P., Flores S.M., Ziff R.M.: Cluster densities at 2-d critical points in rectangular geometries. J. Phys. A Math. Theor. 44, 385002 (2011)
Smirnov S.: Critical percolation in the plane: conformal invariance, Cardy’s formula, scaling limits. C. R. Acad. Sci. Paris 333, 239–244 (2001). arXiv:0909.4499
Smirnov, S.: Towards conformal invariance of 2d lattice models. In: Proceedings of the International Congress of Mathematicians (2006)
Smirnov, S.: Conformal invariance in random cluster models. I. Holomorphic fermions in the Ising model. Ann. Math. 172, 1435–1467 (2010). arXiv:0708.0039
Smirnov, S.: Discrete complex analysis and probability. In: Proceedings of the ICM, Hyderabad (2010)
Schramm O., Sheffield S.: Harmonic explorer and its convergence to \({{\rm SLE}_4}\). Ann. Probab. 33(6), 2127–2148 (2005)
Swendsen R.H., Wang J.-S.: Nonuniversal critical dynamics in Monte Carlo simulations. Phys. Rev. Lett. 58, 86–88 (1987)
Schramm O., Zhou W.: Boundary proximity of SLE. Probab. Theory Relat. Fields 146(3-4), 435–450 (2010)
Simmons, J.J.H., Ziff, R.M., Kleban, P.: Factorization of percolation density correlation functions for clusters touching the sides of a rectangle. J. Stat. Mech. Theory Exp. P02067 (2009)
Zhan D.: The scaling limits of planar LERW in finitely connected domains. Ann. Probab. 36(2), 467–529 (2008)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Denis Bernard.
Rights and permissions
About this article
Cite this article
Jokela, N., Järvinen, M. & Kytölä, K. SLE Boundary Visits. Ann. Henri Poincaré 17, 1263–1330 (2016). https://doi.org/10.1007/s00023-015-0452-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-015-0452-7