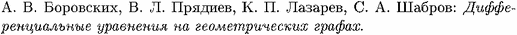Skip to main content
SpringerLink
Log in

New Relations Between Discrete and Continuous Transition Operators on (Metric) Graphs

  • Published:
Integral Equations and Operator Theory Aims and scope Submit manuscript

Abstract

We establish several new relations between the discrete transition operator, the continuous Laplacian and the averaging operator associated with combinatorial and metric graphs. It is shown that these operators can be expressed through each other in a very explicit way. In particular, the averaging operator appears to be closely related to the solutions of the associated wave equation. The machinery used allows one to study a class of infinite graphs without assumption on the local finiteness.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Albeverio S., Brasche J.F., Malamud M.M., Neidhardt H.: Inverse spectral theory for symmetric operators with several gaps: scalar-type Weyl functions. J. Funct. Anal. 228, 144–188 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  2. Alexander S.: Superconductivity of networks. A percolation approach to the effects of disorder. Phys. Rev. B 27, 1541–1557 (1983)

    Article  MathSciNet  Google Scholar 

  3. Ali Mehmeti, F.: Nonlinear waves in networks, Mathematical Research, vol. 80. Akademie Verlag, Berlin (1994)

  4. Ali Mehmeti, F., von Below, J., Nicaise, S. (eds.): Partial Differential Equations on Multistructures, Lecture Notes in Pure and Applied Mathematics, vol. 219. Marcel Dekker, New York (2001)

  5. Behrndt, J., Pankrashkin, K., Post, O. (eds.): Mini-workshop “Boundary value problems and spectral geometry”. Oberwolfach Rep. 9(1), 43–76 (2012)

  6. von Below J.: A characteristic equation associated to an eigenvalue problem on c 2-networks. Linear Algebra Appl. 71, 309–325 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  7. von Below J., Mugnolo D.: The spectrum of the Hilbert space valued second derivative with general self-adjoint boundary conditions. Linear Algebra Appl. 439, 1792–1814 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  8. Berkolaiko, G., Carlson, R., Fulling, S.A., Kuchment, P. (eds.): Quantum Graphs and Their Applications, Contemporary Mathematics, vol. 415. AMS, Providence (2006)

  9. Berkolaiko, G., Kuchment, P.: Introduction to Quantum Graphs, Mathematical Surveys and Monographs, vol. 186. AMS, Providence (2013)

  10. Boutet de Monvel A., Lenz D., Stollmann P.: Sch’nol’s theorem for strongly local forms. Isr. J. Math. 173, 189–211 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  11. Brüning J., Geyler V., Pankrashkin K.: Spectra of self-adjoint extensions and applications to solvable Schrödinger operators. Rev. Math. Phys. 20, 1–70 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  12. Cartwright D.I., Woess W.: The spectrum of the averaging operator on a network (metric graph). Ill. J. Math. 51, 805–830 (2007)

    MathSciNet  MATH  Google Scholar 

  13. Cattaneo C.: The spectrum of the continuous Laplacian on a graph. Monatsh. Math. 124, 215–235 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  14. Cattaneo C., Fontana L.: D’Alembert formula on finite one-dimensional networks. J. Math. Anal. Appl. 284, 403–424 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  15. Chung, F.R.K.: Spectral Graph Theory, CBMS Regional Conference Series in Mathematics, vol. 92. AMS, Providence (1997)

  16. Colin de Verdière, Y.: Spectres de graphes, Cours Spécialisés, vol. 4. SMF (1998)

  17. Dáger, R., Zuazua, E.: Wave Propagation, Observation and Control in 1-d Flexible Multi-structures, Mathématiques et Applications, vol. 50. Springer, Berlin (2005)

  18. Derkach V.A., Malamud M.M.: Generalized resolvents and the boundary value problems for Hermitian operators with gaps. J. Funct. Anal. 95, 1–95 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  19. Exner P.: A duality between Schrödinger operators on graphs and certain Jacobi matrices. Ann. Inst. Henri Poincaré Sect. A: Phys. Théor. 66, 359–371 (1997)

    MathSciNet  MATH  Google Scholar 

  20. Exner, P., Keating, J.P., Kuchment, P., Sunada, T., Teplyaev, A. (eds.): Analysis on Graphs and Its Applications, Proceedings of Symposia in Pure Mathematics, vol. 77. AMS, Providence (2008)

  21. Gorbachuk, V.I., Gorbachuk, M.L.: Boundary Value Problems for Operator Differential Equations, Mathematics and Its Applications: Soviet Series, vol. 48. Kluwer, Dordrecht (1991)

  22. Kopytin, A.V.: Some questions of the theory of evolution problems on networks. Doctoral thesis, Voronezh State University (2002) (in Russian, original title: A. B.

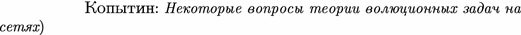
  23. Kopytin, A.V., Pryadiev, V.L.: D’Alembert formula and Laplacian spectrum on a graph with commensurable edges. Vestnik Voronezh. Gos. Univ. Fizika, Matematika, no. 1, pp. 106–109 (2001) (in Russian, original title: A. B. http://www.vestnik.vsu.ru/content/physmath/2001/01/toc_en.asp

  24. Korovina, O.V., Pryadiev, V.L.: Structure of the solution to a mixed problem for the wave equation on a compact geometric graph in the case of a non-zero initial velocity. Izvestiya Saratov. Univ. Matem. Mekh. Inform. 9(3), 37–46 (2009) (in Russian, original title: O. B. 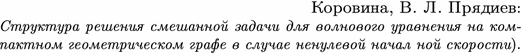http://www.mathnet.ru/eng/isu58

  25. Kuchment, P. (ed.): Special section on quantum graphs. Waves Random Media 14(1) (2004)

  26. Lenz D., Schubert C., Stollmann P.: Eigenfunction expansion for Schrödinger operators on metric graphs. Integr. Equ. Oper. Theory 62, 541–553 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  27. Lenz D., Schubert C., Veselić I.: Unbounded quantum graphs with unbounded boundary conditions. Math. Nachr. 287, 962–979 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  28. Mohar B., Woess W.: A survey on spectra of infinite graphs. Bull. Lond. Math. Soc. 21, 209–234 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  29. Mugnolo, D.: Semigroup Methods for Evolution Equations on Networks. Understanding Complex Systems series, vol. XV. Springer, New York (2014)

  30. Nicaise, S.: Some results on spectral theory over networks, applied to nerve impulse transmission. In: Brezinksi, C., Magnus, A.P., Ronveaux, A. (eds.): Polynômes orthogonaux et applications, Lecture Notes in Mathematics, vol. 1171, pp. 532–541. Springer, New York (1985)

  31. Nicaise, S.: Approche spectrale des problèmes de diffusion sur les réseaux. In: Hirsch, F., Mokobodzki, G. (eds.) Séminaire de Théorie du Potentiel Paris, No. 8, Lecture Notes in Mathematics, vol. 1235, pp. 120–140. Springer, New York (1987)

  32. Pankrashkin K.: Spectra of Schrödinger operators on equilateral quantum graphs. Lett. Math. Phys. 77, 139–154 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  33. Pankrashkin K.: Unitary dimension reduction for a class of self-adjoint extensions with applications to graph-like structures. J. Math. Anal. Appl. 396, 640–655 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  34. Pankrashkin K.: An example of unitary equivalence between self-adjoint extensions and their parameters. J. Funct. Anal. 265, 2910–2936 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  35. Poerschke T., Stolz G., Weidmann J.: Expansions in generalized eigenfunctions of selfadjoint operators. Math. Z. 202, 397–408 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  36. Pokornyi, Yu.V., Penkin, O.M., Borovskikh, A.V., Pryadiev, V.L., Lazarev, K.P., Shabrov, S.A.: Differential equations on geometric graphs (Fizmatlit, Moscow, 2005). In Russian, original title:

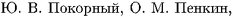
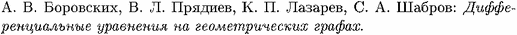
  37. Pokornyi Yu.V., Pryadiev V.L., Borovskikh A.V.: The wave equation on a spatial network. Doklady Math. 67, 10–12 (2003)

    MATH  Google Scholar 

  38. Post, O.: Spectral Analysis on Graph-like Spaces, Lecture Notes in Mathematics, vol. 2039. Springer, New York (2012)

  39. Roth, J.-P.: Le spectre du Laplacien sur un graphe. In: Mokobodzki, G., Pinchon, D. (eds.) Théorie du potentiel, Lecture Notes in Mathematics, vol. 1096, pp. 521–539 (1984)

  40. Saloff-Coste L., Woess W.: Transition operators on co-compact G-spaces. Rev. Matem. Iberoamer. 22, 747–799 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  41. Schmüdgen, K.: Unbounded Self-adjoint Operators on Hilbert Space, Graduate Texts in Mathematics, vol. 265. Springer, New York (2012)

  42. Schubert, C.: Quantengraphen mit zufälligem Potential. Dissertation, Universitätsverlag Chemnitz (2012). http://nbn-resolving.de/urn:nbn:de:bsz:ch1-qucosa-83614

  43. Schubert, C., Seifert, C., Voigt, J., Waurick, M.: Boundary systems and (skew-) self-adjoint operators on infinite metric graphs. Math. Nachr. (to appear). doi:10.1002/mana.201500054

  44. Soardi, P.: Potential Theory on Infinite Networks, Lecture Notes in Mathematics, vol. 1590. Springer, New York (1994)

  45. Weidmann, J.: Spectral Theory of Ordinary Differential Operators, Lecture Notes in Mathematics, vol. 1258. Springer, New York (1987)

  46. Woess, W.: Random Walks on Infinite Graphs and Groups, Cambridge Tracts in Mathematics, vol. 138. Cambridge University Press, Cambridge (2000)

Download references

Author information

Authors and Affiliations

  1. Fakultät für Mathematik und Informatik, Mathematisches Institut, Friedrich-Schiller-Universität Jena, Ernst-Abbe-Platz 2, 07743, Jena, Germany

    Daniel Lenz

  2. Laboratoire de mathématiques (UMR 8628 du CNRS), Université Paris-Sud, Bâtiment 425, 91405, Orsay Cedex, France

    Konstantin Pankrashkin

Authors
  1. Daniel Lenz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Konstantin Pankrashkin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Konstantin Pankrashkin.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lenz, D., Pankrashkin, K. New Relations Between Discrete and Continuous Transition Operators on (Metric) Graphs. Integr. Equ. Oper. Theory 84, 151–181 (2016). https://doi.org/10.1007/s00020-015-2253-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00020-015-2253-2

Mathematics Subject Classification

Keywords

Search

Navigation