Abstract
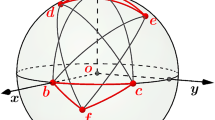
For all unit radius spherical convex k-gons of a fixed diameter \(\pi /2\), where \(3\le k\le n\) and n is odd, the regular spherical triangle has the maximal perimeter, and the regular spherical n-gon attains the maximal area. Besides, for all unit radius spherical convex k-gons of a fixed thickness \(\pi /2\), where \(3\le k\le n\) and n is odd, the regular spherical n-gon attains the minimum perimeter, and the regular triangle reaches the minimal area. Particularly, the reduced spherical polygons reach the maximal thickness (resp. minimal diameter) \(\pi /2\) among all spherical convex polygons of fixed diameter (resp. thickness) \(\pi /2\). Moreover, when n is odd or even, a few conclusions of unit radius spherical convex n-gons are established, respectively.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Audet, C., Hansen, P., Messine, F.: Extremal problems for convex polygons. J. Global Optim. 38(2), 163–179 (2007)
Audet, C., Hansen, P., Messine, F.: The small octagon with longest perimeter. J. Combin. Theory Ser. A. 114(1), 135–150 (2007)
Audet, C., Ninin, J., Messine, F.: Isoperimetric polygons of maximal width. Discrete Comput. Geom. 41(1), 45–60 (2009)
Audet, C., Hansen, P., Svrtan, D.: Using symbolic calculations to determine largest small polygons. J. Global Optim. 81(1), 261–268 (2021)
Araújo, P.V.: Barbier’s theorem for the sphere and the hyperbolic plane. Enseign. Math. 42, 295–309 (1996)
Bezdek, A., Fodor, F.: On convex polygons of maximal width. Arch. Math. (Basel) 74, 75–80 (2000)
Brczky, K.J., Sagmeister, A.: The isodiametric problem on the sphere and in the hyperbolic space. Acta Math. Hungar. 160(1), 13–32 (2020)
Blåsjö, V.: The isoperimetric problem. Amer. Math. Monthly 112, 526–566 (2005)
Chang, Y., Liu, C., Su, Z.: The perimeter and area of reduced spherical polygons of thickness \(\frac{\pi }{2}\). Results Math. 75, 135 (2020)
Datta, B.: A discrete isoperimeteric problem. Geom. Dedicata. 64(1), 55–68 (1997)
Graham, R.L.: The largest small hexagon. J. Combin. Theory Ser. A. 18, 165–170 (1975)
Lassak, M.: Width of spherical convex bodies. Aequationes Math. 89, 555–567 (2015)
Lassak, M.: Reduced spherical polygons. Colloq. Math. 138(2), 205–216 (2015)
Lassak, M.: Diameter, width and thickness of spherical reduced convex bodies with an application to Wulff shapes. Beitr. Algebra Geom. 61, 369–378 (2020)
Mossinghoff, M.J.: A \$1 problem. Amer. Math. Monthly 113(5), 385-402 (2006)
Mossinghoff, M.J.: Isodiametric problems for polygons. Discrete Comput. Geom. 36(2), 363–379 (2006)
Mossinghoff, M.J.: Enumerating isodiametric and isoperimetric polygons. J. Combin. Theory Ser. A. 118(6), 1801–1815 (2011)
Päl, J.: Ein Minimumproblem für Ovale. Math. Ann. 83, 311–319 (1921)
Reinhardt, K.: Extremale Polygone gegebenen Durchmessers. Jahresber. Deutsch. Math.-Verein. 31, 251–270 (1922)
Acknowledgements
The last part of the paper was added according to the suggestion of an anonymous reviewer. The authors would like to thank the referees for their many valuable comments and suggestions that helped us to improve the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supported by NSFC under Grant 11971053.
Rights and permissions
About this article
Cite this article
Liu, C., Chang, Y. Extremal problems for spherical convex polygons. Arch. Math. 118, 435–450 (2022). https://doi.org/10.1007/s00013-021-01698-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00013-021-01698-7