Abstract.
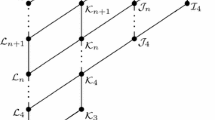
We completely determine all commutative semigroup varieties that are upper-modular elements of the lattice of all semigroup varieties. It is verified that if a semigroup variety is an upper-modular element of this lattice and different from the variety of all semigroups then it is a periodic variety and every nilsemigroup in the variety is commutative and satisfies the identity x2y = xy2.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to George Grätzer and E. Tamás Schmidt on their 70th birthdays
The work was supported by the Russian Foundation for Basic Research (grant No. 06-01-00613).
Received December 30, 2006; accepted in final form February 20, 2008.
Rights and permissions
About this article
Cite this article
Vernikov, B.M. Upper-modular elements of the lattice of semigroup varieties. Algebra univers. 59, 405–428 (2008). https://doi.org/10.1007/s00012-008-2108-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00012-008-2108-7
Keywords and phrases:
- semigroup
- variety
- lattice of subvarieties
- commutative semigroup
- upper-modular element
- distributive lattice
- periodic variety
- nil-variety