Behavior of convex integrand at a d-apex of its Wulff shape and approximation of spherical bodies of constant width

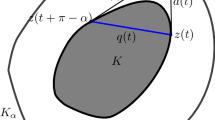
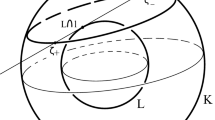
Abstract

Let $\gamma : S^n\rightarrow \mathbb {R}_+$ be a convex integrand and $\mathcal {W}_\gamma$ be the Wulff shape of $\gamma$. A d-apex point naturally arises in a non-smooth Wulff shape, in particular, as a vertex of a convex polytope. In this paper, we study the behavior of the convex integrand at a d-apex point of its Wulff shape. We prove that $\gamma (P)$ is locally maximum, and $\mathbb {R}_+ P\cap \partial \mathcal {W}_\gamma$ is a d-apex point of $\mathcal {W}_\gamma$ if and only if the graph of $\gamma$ around the d-apex point is a piece of a sphere with center $\frac{1}{2}\gamma (P)P$ and radius $\frac{1}{2}\gamma (P)$. As an application of the proof of this result, we prove that for any spherical convex body C of constant width $\tau >\pi /2$, there exists a sequence $\{C_i\}_{i=1}^\infty$ of convex bodies of constant width $\tau$, whose boundaries consist only of arcs of circles of radius $\tau -\frac{\pi }{2}$ and great circle arcs such that $\lim _{i\rightarrow \infty }C_i=C$ with respect to the Hausdorff distance.