Skip to main content
SpringerLink
Log in

Hyers-Ulam stability of an  iterative  equation  for  strictly increasing continuous functions

  • Published:
Aequationes mathematicae Aims and scope Submit manuscript

Abstract

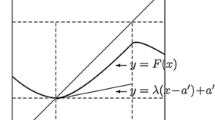
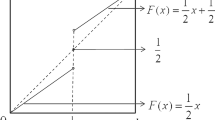
The Hyers-Ulam stability of the iterative equation \(f^n=F\) for continuous functions F was studied under the assumptions that F is a homeomorphism on its range, and the equation has stability on its range. It is important to study the stability of the equation for homeomorphisms on intervals. In this paper, theorems on stability are obtained using the properties of monotonic approximate solutions. The method is based on the stability of two derived iterative equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availibility

No data were used to support this paper.

References

  1. Agarwal, R.P., Xu, B., Zhang, W.: Stability of functional equations in single variable. J. Math. Anal. Appl. 288(2), 852–869 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  2. Babbage, C.: An essay towards the calculus of functions. Philos. Trans. R. Soc. Lond. 105, 389–423 (1815)

    Google Scholar 

  3. Bödewadt, U.T.: Zur iteration reeller funktionen. Math. Z. 49, 497–516 (1944)

    Article  MathSciNet  MATH  Google Scholar 

  4. Cho, Y.J., Suresh Kumar, M., Murugan, V.: Iterative roots of non-PM functions and denseness. Results Math. 73(1), 13-1–18 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  5. Forti, G.L.: Hyers-Ulam stability of functional equations in several variables. Aequ. Math. 50(1–2), 143–190 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  6. Hyers, D.H.: On the stability of the linear functional equation. Proc. Nat. Acad. Sci. U. S. A. 27, 222–224 (1941)

    Article  MathSciNet  MATH  Google Scholar 

  7. Hyers, D. H., Isac, G., Rassias, T. M.: Stability of Functional Equations in Several Variables, vol. 34 of Progress in Nonlinear Differential Equations and their Applications. Birkhäuser Boston, Inc., (1998)

  8. Kuczma, M.: Functional Equations in a Single Variable. Polish Scientific Publishers, Warszawa (1968)

    MATH  Google Scholar 

  9. Kuczma, M., Choczewski, B., Ger, R.: Iterative Functional Equations. Encyclopedia of Mathematics and Its Applications, vol. 32. Cambridge University Press, Cambridge (1990)

  10. Li, L., Yang, D., Zhang, W.: A note on iterative roots of PM functions. J. Math. Anal. Appl. 341(2), 1482–1486 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  11. Li, L., Song, W., Zeng, Y.: Stability for iterative roots of piecewise monotonic functions. J. Inequal. Appl. 2015, 399 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  12. Li, L., Zhang, W.: The question on characteristic endpoints for iterative roots of PM functions. J. Math. Anal. Appl. 458(1), 265–280 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  13. Li, L., Liu, L.: Decreasing case on characteristic endpoints question for iterative roots of PM functions. J. Differ. Equ. Appl. 25(3), 396–407 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  14. Liu, L., Jarczyk, W., Li, L., Zhang, W.: Iterative roots of piecewise monotonic functions of nonmonotonicity height not less than 2. Nonlinear Anal. 75(1), 286–303 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  15. Liu, L., Li, L., Zhang, W.: Open question on lower order iterative roots for PM functions. J. Differ. Equ. Appl. 24(5), 825–847 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  16. Murugan, V., Palanivel, R.: Non-isolated, non-strictly monotone points of iterates of continuous functions. Real Anal. Exchange 46(1), 51–82 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  17. Murugan, V., Palanivel, R.: Iterative roots of continuous functions and Hyers-Ulam stability. Aequat. Math. 95(1), 107–124 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  18. Rassias, T.M.: On the stability of the linear mapping in Banach spaces. Proc. Am. Math. Soc. 72(2), 297–300 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  19. Rassias, T.M.: On the stability of functional equations in Banach spaces. J. Math. Anal. Appl. 251(1), 264–284 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  20. Xu, B., Zhang, W.: Hyers-Ulam stability for a nonlinear iterative equation. Colloq. Math. 93(1), 1–9 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  21. Xu, B., Zhang, W.: Construction of continuous solutions and stability for the polynomial-like iterative equation. J. Math. Anal. Appl. 325(2), 1160–1170 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  22. Zhang, W.: PM functions, their characteristic intervals and iterative roots. Ann. Polon. Math. 65(2), 119–128 (1997)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors thank the referees for their valuable comments and suggestions. The first author thanks the National Institute of Technology Karnataka, Surathkal, for supporting this work.

Funding

There is no funding to support this paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, School of Advanced Sciences, Vellore Institute of Technology, Vellore, Tamil Nadu,  632 014, India

    Rajendran Palanivel

  2. Department of Mathematical and Computational Sciences, National Institute of Technology Karnataka, Surathkal, Mangaluru,  575 025, India

    Veerapazham Murugan

Authors
  1. Rajendran Palanivel
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Veerapazham Murugan
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed equally.

Corresponding author

Correspondence to Rajendran Palanivel.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Ethical approval

This paper does not contain any studies involving with human participants/animals.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Palanivel, R., Murugan, V. Hyers-Ulam stability of an  iterative  equation  for  strictly increasing continuous functions. Aequat. Math. 97, 575–595 (2023). https://doi.org/10.1007/s00010-022-00935-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00010-022-00935-w

Keywords

Mathematics Subject Classification

Search

Navigation