On convex bodies with isoptic chords of constant length

Abstract

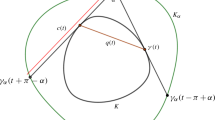
Let K be a strictly convex body in ${\mathbb {R}}^2$ with differentiable boundary and let z, w be two points in its boundary. We say that [z, w] is an $\alpha$-chord of K if the lines tangent to K at z and w intersect at an angle $\alpha$. In this paper we study convex bodies with $\alpha$-chords of constant length. We prove that K is a Euclidean disc whenever it satisfies one of the following conditions: K is of constant width; the $\alpha$-isoptic of K is a circle; K has rotational symmetry of angle $\pi -\alpha$. Using this result, we deduce that convex bodies with $\pi /2$ of $\pi /3$-chords of constant length must also be Euclidean discs. Finally, we prove that convex bodies that have $\alpha$-chords and $\beta$-chords of constant length, where $\alpha$ and $\beta$ are supplementary angles, are also Euclidean discs provided that $\alpha$ is an irrational multiple of $\pi$ or $\alpha = p \pi /(2k+1)$, where $p,k\in {\mathbb {N}}$.