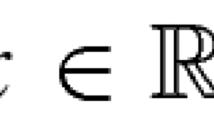Skip to main content
SpringerLink
Log in

Existence of Solution for a Class of Variational Inequality in Whole \({\mathbb {R}}^N\) with Critical Growth: The Local Mountain Pass Case

  • Published:
Mediterranean Journal of Mathematics Aims and scope Submit manuscript

Abstract

In this paper, we study the existence of solution for a class of variational inequality in whole \({\mathbb {R}}^N\) where the nonlinearity has a critical growth for \(N \ge 2.\) By combining a penalization scheme found in del Pino and Felmer (Calc Var 4:121–137, 1996) with a penalization method due to Bensoussan and Lions (Applications des inéquations variationelles en contrôle stochastique. Dunod, Paris, 1978), we improve a recent result by Alves et al. (J Math Anal Appl 494:124672, 2021).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data Availability

My manuscript has no associate data.

References

  1. Alves, C., Barros, L., Torres, C.: Existence of solution for a class of variational inequality in whole \({{\mathbb{R} }}^N\) with critical growth. J. Math. Anal. Appl. 494, 124672 (2021)

    Article  MATH  Google Scholar 

  2. Alves, C.O., Côrrea, F.J.S.A.: Multiplicity of positive solutions for an obstacle problem in \({{\mathbb{R} }}\). Prog. Nonlinear Differ. Equ. Appl. 85, 23–28 (2010)

    MathSciNet  MATH  Google Scholar 

  3. Alves, C.O., Pereira, D.S.: Multiplicity of multi-bump type nodal solutions for a class of elliptic problems with exponential critical growth in \({{\mathbb{R} }}^2\). Proc. Edinb. Math. Soc. 2(60), 273–297 (2017)

    Article  MATH  Google Scholar 

  4. Alves, C.O., Souto, M.A.S.: Multiplicity of positive solutions for a class of problems with exponential critical growth in \({\mathbb{R} }^{2}\). J. Differ. Equ. 244, 1502–1520 (2008)

    Article  MATH  Google Scholar 

  5. Alves, C.O., Barros, L.: Existence and multiplicity of solutions for a class of elliptic problem with critical growth. Monatsh. Math. 187, 195–215 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  6. Ambrosetti, A., Rabinowitz, P.H.: Dual variational methods in critical point theory and applications. J. Funct. Anal. 14, 349–381 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  7. Baiocchi, C., Capelo, A.: Variational and Quasivariational Inequalities: Applications to Free Boundary Problems. Wiley, New York (1984)

    MATH  Google Scholar 

  8. Bensoussan, A., Lions, J.-L.: Applications des inéquations variationelles en contrôle stochastique. Dunod, Paris (1978)

    MATH  Google Scholar 

  9. Campa, I., Degiovanni, M.: Subdifferential calculus and nonsmooth critical point theory. SIAM J. Optim. 10(4), 1020–1048 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  10. Crank, J.: Free and Moving Boundary Problems. Clarendran Press, Oxford (1984)

  11. Chipot, M., Yeressian, K.: On some variational inequalities in unbounded domains. Boll. del UMI (9) V, 243–262 (2012)

    MathSciNet  MATH  Google Scholar 

  12. Carl, S., Le, V.K., Motreanu, D.: Nonsmooth variational problems and their inequalities, comparison principles and applications. Springer, New York (2007)

    Book  MATH  Google Scholar 

  13. Cao, D.M.: Nontrivial solution of semi-linear elliptic equation with critical exponent in \({\mathbb{R} }^2\). Commun. Partial Differ. Equ. 17, 407–435 (1992)

    Article  Google Scholar 

  14. Corvellec, J.N., Degiovanni, M., Marzocchi, M.: Deformation properties for continuous functionals and critical point theory. Topol. Methods Nonlinear Anal. 1(1), 151–171 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  15. Degiovanni, M., Zani, S.: Multiple solutions of semilinear elliptic equations with one-sided growth conditions, nonlinear operator theory. Math. Comput. Model. 32(11–13), 1377–1393 (2000)

    Article  MATH  Google Scholar 

  16. Degiovanni, M., Marzocchi, M.: A critical point theory for nonsmooth functionals. Ann. Mat. Pura Appl. (4) 167, 73–100 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  17. del Pino, M., Felmer, P.L.: Local mountain passes for semilinear elliptic problems in unbounded domains. Calc. Var. 4, 121–137 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  18. Duvaut, G., Lions, J.-L.: Inequalities in Mechanics and Physics. Springer, Berlin (1976)

    Book  MATH  Google Scholar 

  19. Fang, M.: Degenerate elliptic inequalities with critical growth. J. Differ. Equ. 232(2), 441–467 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  20. Fichera, G.: Sul problema elastostatico di Signorini con ambigue condizioni al contorno. Atti Accad. Naz. Lincei VIII. Ser. Rend. Cl. Sci. Fis. Mat. Nat. 34, 138–142 (1963)

    MathSciNet  MATH  Google Scholar 

  21. Figueiredo, G.M., Furtado, M., Montenegro, M.: An obstacle problem in a plane domain with two solutions. Adv. Nonlinear Stud. 14, 327–337 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  22. Figueiredo, D.G., Miyagaki, O.H., Ruf, B.: Elliptic equations in \({{\mathbb{R} }}^2\) with nonlinearity in the critical growth range. Calc. Var. Partial Differ. Equ. 3, 139–153 (1995)

    Article  MATH  Google Scholar 

  23. Friedman, A.: Free boundary problems in science and technology. Not AMS 47(8), 854–861 (2000)

    MathSciNet  MATH  Google Scholar 

  24. Gongbao, L.: Some properties of weak solutions of nonlinear scalar field equations. Ann. Acad. Sci. Fenn. Ser. A 14, 27–36 (1989)

    MATH  Google Scholar 

  25. Jianfu, Y.: Positive solutions of quasilinear elliptic obstacle problems with critical exponents. Nonlinear Anal. 25(12), 1283–1306 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  26. Jianfu, Y.: Positive solution of an obstacle problems. Ann. Fac. Sci. Toulouse Math., \(6^{{\acute{{{\rm e}}}{{\rm me}}}}\) Série, tome. 4(2), 339–366 (1995)

  27. Kavian, O.: Introduction a la Theorie Des Points Critiques: Et Applications Aux Problemes Elliptiques. Springer, Heildelberg (1993)

    MATH  Google Scholar 

  28. Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and Their Applications. Academic Press, New York (1980)

    MATH  Google Scholar 

  29. Lions, P.L.: The concentration-compactness principle in the calculus of variations. The limit case, 1 & 2. Math. Iberoam. 1, 145–201 and 46–121 (1985)

  30. Lions, J., Stampacchia, G.: Variational inequalities. Commun. Pure Appl. Math. 20, 493–519 (1967)

  31. Mancini, G., Musina, R.: Holes and obstacles. Ann. Inst. H. Poincaré Anal. Non Linéaire Sect. C 5(4), 323–345 (1988)

  32. Magrone, P., Mugnai, D., Servadei, R.: Multiplicity of solutions for semilinear variational inequalities via linking and \(\nabla \)-theorems. J. Differ. Equ. 228, 191–225 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  33. Magrone, P., Servadei, R.: A stability result for mountain pass type solutions of semilinear elliptic variational inequalities. Adv. Nonlinear Stud. 9(4), 387–405 (2002)

    MathSciNet  MATH  Google Scholar 

  34. Matzeu, M., Servadei, R.: A Linking type method to solve a class of semilinear elliptic variational inequalities. Adv. Nonlinear Stud. 2(1), 1–17 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  35. Matzeu, M., Servadei, R.: Semilinear elliptic variational inequalities with dependence on the gradient via mountain pass techniques. Nonlinear Anal. 72, 4347–4359 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  36. Matzeu, M., Servadei, R.: Stability for semilinear elliptic variational inequalities depending on the gradient. Nonlinear Anal. 74, 5161–5170 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  37. Moser, J.: A new proof de Giorgi’s theorem concerning the regularity problem for elliptic differential equations. Commun. Partial Differ. Equ. 13, 457–468 (1960)

    MathSciNet  MATH  Google Scholar 

  38. Monneau, R.: A brief overview on the obstacle problem. In: European Congress of Mathematics, vol. II (Barcelona, 2000). Progress in Mathematics, vol. 202, pp. 303–312. Birkhäuser, Basel (2001)

  39. Motreanu, D., Rădulescu, V.D.: Variational and Non-variational Methods in Nonlinear Analysis and Boundary Value Problems. Kluwer Academic, Dordrecht

  40. Panagiotopoulos, P.D.: Hemivariational Inequalities: Applications to Mechanics and Engineering. Springer, New York (1993)

    Book  MATH  Google Scholar 

  41. Rodrigues, J.F.: Obstacle Problems in Mathematical Physics. Mathematics Studies, vol. 134. Elsevier, Amsterdam (1987)

    Book  MATH  Google Scholar 

  42. Szulkin, A.: Minimax principles for lower semicontinuous functions and applications to nonlinear boundary value problems. Ann. Inst. H. Poincaré Anal. Non Linéaire 3, 77–109 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  43. Teka, K.H.: The obstacle problem for second order elliptic operators in nondivergence form. Thesis(Ph.D.)-Kansas States University (2012)

  44. Troianiello, G.M.: Elliptic Differential Equations and Obstacle Problems. The University Series in Mathematics, Springer, Berlin (1987)

    Book  MATH  Google Scholar 

  45. Willem, M.: Minimax Theorems. Birkhäuser, Basel (1996)

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Unidade Acadêmica de Matemática, Universidade Federal de Campina Grande, Campina Grande, PB, 58429-970, Brazil

    Claudianor O. Alves

  2. Unidade Acadêmica de Física e Matemática, Universidade Federal de Campina Grande, Cuité, PB, 58175-000, Brazil

    Luciano M. Barros

  3. Departamento de Matemáticas, Universidad Nacional de Trujillo, Av. Juan Pablo II s/n., Trujillo, Peru

    César E. Torres Ledesma

Authors
  1. Claudianor O. Alves
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Luciano M. Barros
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. César E. Torres Ledesma
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors reviewed the manuscript.

Corresponding author

Correspondence to César E. Torres Ledesma.

Ethics declarations

Conflict of interest

This work does not have any conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Alves, C.O., Barros, L.M. & Torres Ledesma, C.E. Existence of Solution for a Class of Variational Inequality in Whole \({\mathbb {R}}^N\) with Critical Growth: The Local Mountain Pass Case. Mediterr. J. Math. 20, 239 (2023). https://doi.org/10.1007/s00009-023-02450-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00009-023-02450-x

Keywords

Mathematics Subject Classification

Search

Navigation